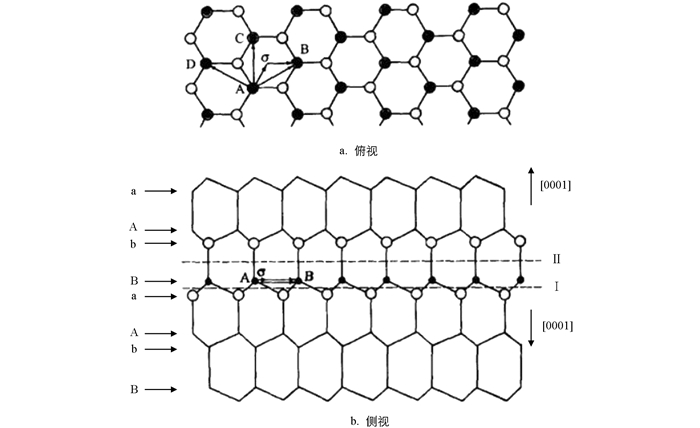
CoO是闪锌矿/纤锌矿型晶体结构，属于密排六角点阵. (CoO)的钴(Co)和氧(O)由六角排列的原子面按AaBbAaBb次序堆垛而成其中. A，B面表示Co原子面，a，b面表示O原子面，但是，六角排列面间距离和金刚石结构的原子面间距类似，如A和a面之间的距离是a和B面之间距离的3倍，这主要是由于纤锌矿中的共价键仍然保持了正四面体结构. 结构的俯视和侧视如图 1a和图 1b所示，由晶体结构知，其晶格常数a=2.51×10^-10m，一个Co原子最近邻的原子是O原子，共5个，次近邻的是Co原子，有2个，距离为1.633a，再次近邻为Co原子，有4个，距离为$\sqrt 3 a$，其余以此类推.

在原子相互作用势的作用下，原子在平衡位置作非简谐振动. 设一个原子平均相互作用势为φ(r)，将它对平衡时的偏离δ=r-r₀展开，偏离很小时，有：

其中：ε₀称为简谐系数，ε₁和ε₂分别称为第一、第二非谐系数. 具体大小取决于原子相互作用势的具体形式.

CoO中，O与O以及O与Co原子间相互作用势为^[5]：

式中：$\frac{{{q_1}{q_2}}}{r}$以波尔半径a₀=0.053 nm为单位，当以eV为能量单位时，而nm为长度单位，$\frac{{{q_1}{q_2}}}{r}$ 应写为$14.421 \; 83 \frac{{{q_1}{q_2}}}{r}$，于是(2)式变为：

其中A，C以及ρ都是经验参数，其具体数值见表 1.

Co原子间相互作用可写为^[6]：

其中：λ_D为平均德拜波长，g为与成键相关量，n为键强参数，具体数值见表 2.

利用原子的平均相互作用势$\varphi(r)=\frac{1}{2} \sum\limits_{i j} u_{i}\left(r_{i j}\right)$，考虑原子间的最近邻、次近邻、再次近邻关系，O和Co的平均相互作用能分别近似为：

由(1)、(3)、(4)、(5)式可求得氧原子简谐系数ε_0O、第一非简谐系数ε_1O和第二非简谐系数ε_2O以及钴原子简谐系数ε_0Co、第一非简谐系数ε_1Co和第二非简谐系数ε_2Co分别为：

利用质心运动定理，得到CoO的简谐系数ε_0CoO、第一非简谐系数ε_1CoO和第二简谐系数ε_2CoO分别为：

按照固体理论，每个原子都在作振动，采用德拜模型，有一个最大振动频率ω_D(德拜频率)，简谐近似下为ω_D常数，它与简谐系数ε₀的关系为ω_D0=(ε₀/M)^1/2，在非简谐振动下为^[7-8]：

德拜温度θ_D是晶格动力学中一个重要参量和特征温度，它代表德拜模型中原子都以ω_D振动时晶体所具有的温度. 文献[9]采用实验方法对ZIF-67内核材料(CoO)结构与德拜温度因子进行了研究，但未研究德拜温度与温度的关系.

这里，由(7)式和(8)式，利用德拜温度与德拜频率的关系${k_{\rm{B}}}{\theta _{\rm{D}}} = \hbar {\omega _{\rm{D}}}$(${{k_{\rm{B}}}, \hbar }$分别是玻尔兹曼常数和普朗克常数)，再考虑到原子非简谐振动后，并按质量加权平均可得到氧化钴的德拜温度θ_D随温度T的变化关系为：

文献[10]指出，材料在热、光、化学等内外因素作用下，性能逐渐降低，甚至完全丧失其使用价值，这种现象被称作材料的老化. 除材料老化以及缺陷等会影响材料热力学性能的稳定性外，温度无疑是另一个重要因素. 由于原子的非简谐振动，温度的变化引起膨胀或收缩，使原子的组成结构和相互作用情况发生变化，导致热膨胀性以及其他性质改变，直接影响材料的工作寿命. 从微观上看，原子振动的非简谐项的存在，使原子振动不是等振幅的、能量不变的简谐振动，而是能量随时间衰减的阻尼振动，原子非简谐振动对原子振动阻尼作用的大小用阻尼系数β描述，而它的倒数称为特征寿命，即η=1/β，它表示材料性能由1变为1/e≈1/2.73所需的时间.

文献[11]已证明，阻尼系数随温度的变化为：

式中：κ=(ω-ω^′)/ω为阻尼对原子振动频率的影响参量，体现非谐效应、声子与声子、声子与缺陷相互作用对原子振动频率的影响和阻尼，是可调参数，可由理论推导或由理论结果与实验比较来确定. 一般情况下，κ值很小，对小阻尼情况，κ值在10^-9~10^-11之间. 这里取κ=4.5×10^-10，而ω₀=(ε₀/M)^1/2是T=0 K时体内原子的振动频率.

由(10)式得到特征寿命随温度的变化为：

蓄热性能由热容量体现. 热容量包括电子的贡献和声子的贡献之和：C_v=C_e+C_p，其中电子贡献的热容很小，只在低温时才显示. 对CoO应用的温度环境，可不考虑电子对热容量的贡献. 采用德拜模型，可得同种原子组成晶体的定容比热容量为^[12]：

式中的R为气体普适常数，$f_{\mathrm{D}}\left(\frac{\theta_{\mathrm{D}}}{T}\right)$是以θ_D/T为变量的德拜函数，μ为摩尔质量.

由(10)和(11)，CoO的定容比热c_v^′为：

式中：μ_Co和μ_O分别为Co和O的摩尔质量，R为摩尔气体常数，Ω为晶胞体积，N₀为阿伏伽德罗常数，而

由已知参量求得CoO中各原子的简谐系数、第一非简谐系数和第二非简谐系数(表 3).

由氧原子质量M_O=0.265 68×10^-25 kg，Co原子质量M_Co=0.978 03×10^-25 kg，求得钴(Co)和氧(O)的摩尔质量μ_Co=58×10^-3 kg，μ_O=16×10^-3 kg.

则简谐系数为：

第一非简谐系数为：

第二非简谐系数为：

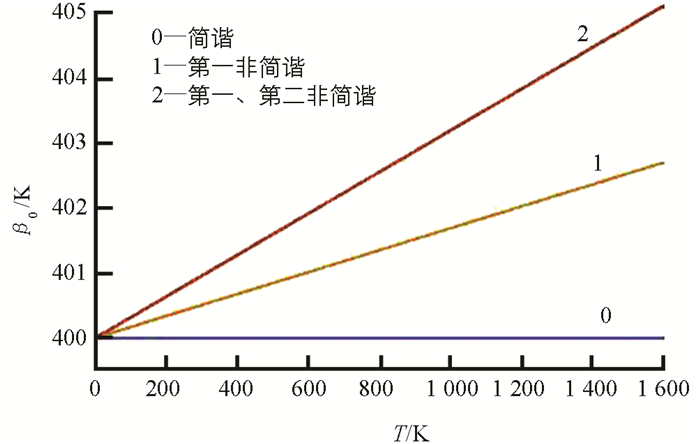
将这些数据代入(9)式，得到CoO的德拜温度θ_D随温度T的变化见图 2. 图 2中的曲线0，1，2分别是简谐近似、只计算到第一非简谐项、同时计算到第一和第二非简谐项的结果.

由图 2可知：①简谐近似下CoO的德拜温度为常量，接近400 K；②考虑非简谐效应后，其德拜温度随温度升高而线性增大；③温度愈高，非简谐的值增大得更明显，即非简谐效应愈明显.

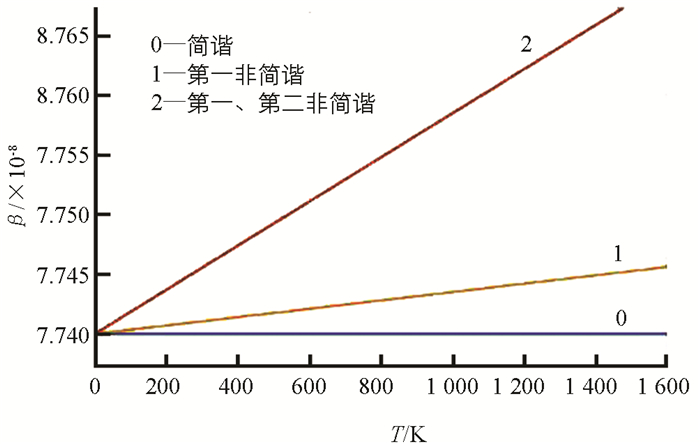
同理，将上述数据代入(10)式，得到CoO的阻尼系数随温度的变化(图 3). 图 3中曲线0，1，2分别是简谐、考虑到第一非简谐、同时考虑到第一和第二非简谐的结果.

由图 3可知：①简谐近似下氧化钴的阻尼系数为常量，接近8.74×10^-8；②考虑非简谐效应后，其阻尼系数随温度升高而增大，其中，第二非简谐比第一非简谐的值增大得更明显；与简谐近似相比，温度从0增至1 300 K时，阻尼系数稍有增加，为0.023×10^-8，与德拜温度相比，非简谐项对阻尼系数的影响更加缓慢；③温度愈高，非简谐效应愈明显.

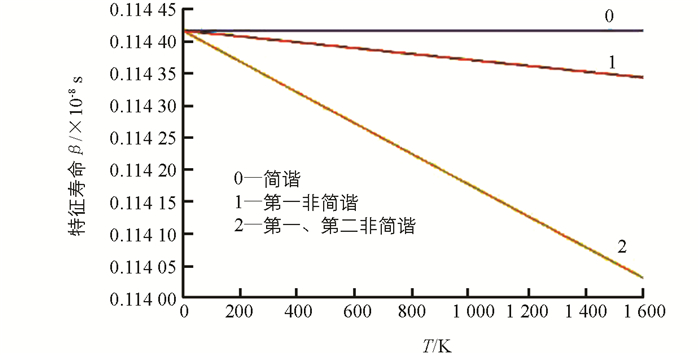
将上述数据代入(11)式，得到氧化钴的特征寿命随温度的变化(图 4). 图 4中曲线0，1，2分别是简谐、考虑到第一非简谐、同时考虑到第一和第二非简谐的结果.

由图 4可知：①简谐近似下氧化钴的特征寿命为常量，接近0.114 416 476×10⁸s；②考虑非简谐效应后，其值随温度升高而减少，其中，第二非简谐比第一非简谐的值减少得更快；与简谐近似相比，温度从0增至1 300 K时，特征寿命稍有减少，约为3.2×10⁴s(即减少约0.000 2%)，与德拜温度相比，非简谐项对特征寿命的影响更加缓慢；③温度愈高，非简谐效应愈明显.

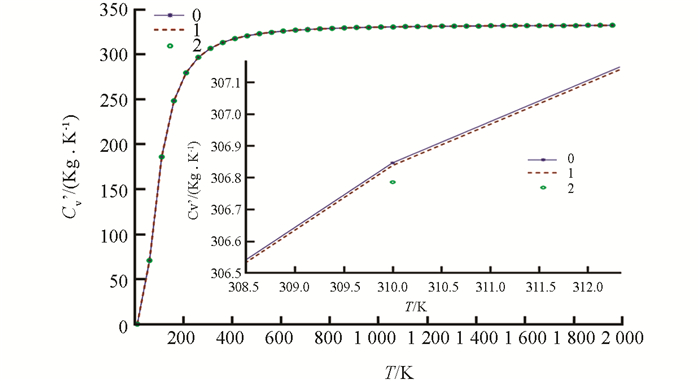
类似地，将上述数据代入(14)、(15)式，得到CoO的定容比热c_v^′随温度T的变化关系(图 5)，图 5中曲线0，1，2的分别是简谐、考虑到第一非简谐、同时考虑到第一和第二非简谐的结果.

为了比较，表 4列出文献[4]给出的与CoO相近的氧化镍(NiO)的定容比热随温度T的变化数据和本文对CoO的计算值. 可看出，相同温度下，NiO的定容比热大于CoO的值，原因可从Co的德拜温度(445 K)和原子质量比Ni的德拜温度(450 K)和原子质量小得以说明. 还可以看出，本研究计算的氧化钴的定容比热随温度T的变化规律，与文献[4]对NiO的变化规律相近.

由图 5知：(1) CoO的定容比热容量随温度升高而非线性增大.温度较低(如T＜800 K)时，增大得较快，其中温度很低(如T＜100 K)时遵从c_v∝T³变化规律；而温度较高(如T＞1 300 K)时，则变化较慢；温度很高时将逐渐趋于常量；(2) 与简谐近似时的热容量值相比，考虑到非简谐振动后，热容量的值稍有减小. 非简谐的比热容与简谐近似时的比热容的差(即非简谐效应对热容量的影响)随温度的升高而增大，即温度愈高，非简谐效应愈显著.

1) CoO的德拜温度、阻尼系数、特征寿命和定容比热均随温度变化而变化，其变化规律由(9)式、(10)式、(11)式和(14)式决定；

2) CoO的德拜温度、阻尼系数、和定容比热均随温度升高而增大，而特征寿命却减少，其中，德拜温度、阻尼系数和特征寿命随温度的变化非常缓慢，每升高1 K，德拜温度仅升高0.001%，而阻尼系数仅升高0.000 2%，特征寿命减少约0.000 2%. 而定容比热随温度升高是非线性增大，其中，温度较低时，近似遵从T³变化规律；温度较高时，趋于常量. 在100 K＜T＜1 300 K的温度范围内，则变化较快；

3) 非简谐振动对材料的德拜温度、阻尼系数、特征寿命和定容比热有重要影响. 若不考虑非简谐效应，则CoO的德拜温度、阻尼系数和特征寿命为常量，考虑到原子非简谐振动后，则随温度的变化而变化. 非简谐效应会使热容量的值比不考虑时的值稍有减小，且温度愈高，非简谐效应愈显著.