-
开放科学(资源服务)标志码(OSID):

-
目前,对企业食品安全生产实证研究比较典型的做法是用学术界提出的质量调整成本模型(Quality-adjusted Cost Model)来刻画,并将其设定为超越对数成本函数(Translog Cost Function)形式. 近年来,这一函数在国外得到了广泛应用:Kitenge运用该方法分析食品和农产品进口对美国农业部门的影响[1],Shin等分析了近海渔业的规模经济[2],Bhattacharya对美国烟草业技术创新进行了分析[3],Modrego等研究了“新冠”疫情对智利就业的影响[4],Bagadeem通过研究指出沙特电信行业规模报酬递增[5],Maziotis等研究了2010-2017年智利水和排污行业规模经济和范围经济的存在性[6]. 国内学者也运用该函数展开相应的研究,陈林等对上市零售企业的规模经济效应进行测度[7],章玉等分析了财政补贴对公交企业成本函数和生产率的变动效果和影响程度[8],查冬兰等对我国工业部门能源与非能源要素之间的替代关系进行了分析[9],林善浪等检验了劳动力转移与农业机械化之间的关系[10],陈林对混合所有制改革进行了分析[11]. 笔者之一曾对这一模型进行了拓展,发展出该模型的一般形式,即超越对数成本面板方程,对文献中关于该模型设定的各种形式作出了有力解释[12];并对模型的特征进行了分析,包括:超越对数成本方程为二阶泰勒展开式、超越对数成本方程相关参数约束条件、系统结构模型扰动项方差—协方差矩阵为奇异矩阵及其处理等[13]. 目前,学术界对该模型的设定还未作分析,为此,本文将从模型形式选择检验、严重多重共线性处理和模型可识别处理等方面作进一步研究,以期为超越对数成本函数的模型设定提供相应借鉴.
全文HTML
-
本文选取的样本数据来源于中国工业企业数据库,考虑到数据的可获得性,最终选取了2004-2007年度样本量最大的肉制品及副产品加工企业(小类编码为1 352),它隶属于屠宰及肉类加工(中类编码为135),归口于农副食品加工业(大类编码为13),属于制造业(C门类). 定义相关指标:销售收入为POR,利润总额为TP,应交所得税为ITP,本年工资为WP,福利费为WEL,K为资产,直接材料为DM,两种生产要素分别为劳动L、原材料M,两种要素投入所占成本份额分别表示为Sl和Sm. 相应地,笔者之一的前期成果对相关变量的界定进行了详细讨论[12],总成本C=POR-TP+ITP,工资Wl=WP+WEL,原材料投入量Wm=DM,产品质量Q=TP/K,需求变动因素Z由企业所在地区的城镇居民人均可支配收入表示,Sl=Wl/C、Sm=Wm/C. 本文采用Stata 11软件处理数据、编写相关程序、得出回归结果(限于篇幅,本文省略了相关数学证明、运行程序和部分回归结果).
-
在前期研究中,笔者在Braeutigam等[14]、Gertler等[15]提出的框架下,结合选取的样本数据和我国企业的特殊情况对该框架作了拓展,在此继续沿用这一成果:质量调整成本函数为C=C(Y,S,Q,W,K),均衡食品安全方程为S=S(Q,W,K,P,Z),其中,C为总成本,Y为总产量,S为食品安全,Q为产品质量,W为要素价格,K为资产,P为产品价格,Z为需求变动因素. 在研究中需解决质量调整成本函数的模型形式设定. 一方面,从目前国内外的研究来看,各种文献采取了超越对数成本函数形式,该函数是经验研究中最频繁使用的灵活函数形式,在众多奇异的函数形式中成为最可靠与最受欢迎的函数[16]. 其特征为:包含每个解释变量的一次项、二次项和变量之间的交互项. 另一方面,该函数的难点在于产品质量和食品安全均为无法观测到的变量. 其中,学术界已解决了产品质量的量化问题[17],却未分析食品安全的量化处理. 为此,我们试着将涉及食品安全变量的各项均纳入一个统一的“方框”变量αi,这正是面板数据模型的特征. 考虑h=1,…,H种生产要素的情况,最终将质量调整成本函数拓展为超越对数成本面板方程:
式(1)中,i为观测值个体,i=1,…,N;t为时间,t=2004,…,2007;h=1,…,H种要素;υit为随机扰动项;αi为所有涉及食品安全变量的项,等于
$\alpha_{y s} \ln Y_{i t} \ln S_{i t}+\beta_{k s} \ln K_{i t} \ln S_{i t}+\sum\limits_{h=1}^H \gamma_{w s \cdot h} \ln S_{i t} \ln W_{i t \cdot h}+\theta_{q s} \ln Q_{i t} \ln S_{i t}+\eta_s \ln S_{i t}+1 / 2 \eta_{s s}\left(\ln S_{i t}\right)^2$ . 由式(1)可导出劳动的成本份额方程:式(1)和(2)组成系统结构模型,采用似不相关估计提高估计的效率. 其中,食品安全S是无法观测到的,需要把均衡食品安全方程代入其中,将系统结构模型转化为系统简化模型. 经过下文的模型识别和严重多重共线性处理后,均衡食品安全方程设定为:
式(1)为面板方程,那么首先面临着形式选择问题:混合模型(POOL)、固定效应模型(FE)和随机效应模型(RE),下面对此进行检验.
1.1. 数据来源和变量说明
1.2. 模型设定
-
结合样本数据,在式(1)中检验的基本思路为对3种形式进行两两对比. 在对模型形式选择问题分析之前,首先需要对扰动项是采用普通标准差还是稳健标准差进行检验.
-
普通标准差计算方法是在假定扰动项为独立同分布(Independently Identically Distribution,简记IID)的情况下进行的,但在现实中,每个企业不同年份之间的扰动项一般存在自相关(即组内自相关),因此,在这种情况下普通标准差的估计并不准确. 为此,需要检验式(1)的扰动项是否存在自相关. 对于这个问题,Wooldridge提出了一个对组内自相关的检验方法[18],其原假设表达为H0:式(1)不存在一阶自相关,备择假设表达为H1:式(1)存在一阶自相关. 根据运行结果,p=0.002 8<0.01,故显著拒绝原假设,这说明式(1)中的扰动项存在一阶组内自相关. 所以,在检验中,将统一采用聚类变量为“肉制品企业法人单位代码”的聚类稳健标准差. 下面分别对模型形式的选择进行检验.
-
在这两类模型检验中,原假设为H0:式(1)υit=0(POOL模型),备择假设为H1:式(1)υit≠0(FE模型). 根据运行结果,p=0.000 0<0.01,故在1%水平上拒绝原假设,即存在个体效应(选择FE模型). 需要说明的是,由于未使用聚类稳健标准误,故并不能保证这个F检验的有效性;不过由于p值很小(接近0),即使按聚类标准差来计算F值,大致也能拒绝原假设. 为了使这一结论得到肯定性的验证,可以进一步采用“最小二乘虚拟变量模型”(Least Square Dummy Variable Model,简记LSDVM)进行考察. 从回归结果来看,大多数个体虚拟变量均都显著(p<0.1),可以确信拒绝“所有个体虚拟变量都为0”的原假设,即存在个体效应,应选择FE模型.
-
在此检验中,Breusch和Pagan提供了一个检验个体效应的LM检验[19]. 原假设为H0:式(1)随机扰动项的方差σv2=0(不存在个体效应,即POOL),备择假设为H1:式(1)σv2≠0(存在个体效应,即RE). 根据运行结果,p=0.000 0<0.01. LM检验拒绝原假设,因此,应该选择RE模型.
-
无论是从POOL与FE之间的检验还是从POOL与RE之间的检验来看,都得出式(1)存在个体效应的结论. 接下来是在FE与RE之间进行选择检验,需要注意的是,如果采用聚类稳健标准差,则传统的豪斯曼检验会失效. 我们采取Bootstrap自助法来解决这一问题.
根据Hausman提出的FE与RE模型检验的基本原理[20],在式(1)中,检验的原假设为H0:αi与各解释变量不相关(RE),备择假设为H1:αi与各解释变量相关(FE). 在备择假设H1情况下,
$\hat{\beta}_{F E}$ 为一致估计量,但$\hat{\beta}_{R E}$ 是不一致的[21]. 事实上,可将原假设和备择假设的检验逻辑思维进行等价转换,原假设为H0:αi与各解释变量不相关(RE)⇔H0:$\left(\hat{\beta}_{F E}-\hat{\beta}_{R E}\right) \stackrel{p}{\longrightarrow} 0$ ,即检验RE相当于检验FE估计量与RE估计量之差依概率收敛于0;备择假设为H1:αi与各解释变量相关(FE)⇔H1:$\left(\hat{\beta}_{F E}-\hat{\beta}_{R E}\right)$ 难以依概率收敛于0. 这种转换将为我们编写Bootstrap程序提供了基本依据. Cameron和Trivedi认为,在进行假设检验或区间估计时,自助样本的个数取999[22]. 因此,本文将进行999次自助抽样. 根据运行结果,得出包含常数项在内的21个解释变量的卡方值为28.96;检测统计量x2(20,28.96)(20为$\hat{\beta}_{F E}$ 的维度,即随时间而变的解释变量个数,不包括常数项)的p=0.088 5<0.1,即在10%显著性水平上拒绝原假设,从而接受“αi与各解释变量相关”的备择假设,这表征式(1)应该采用固定效应模型(FE). -
由于式(1)采取固定效应模型,传统估计FE模型的方法是消掉无法观测的变量(包括这里的食品安全),这将影响下一步的分析. 在此,我们转而对FE模型进行另类的表达,即将式(1)中的方框变量αi“打开”,具体考察αi的形式,这是本文有别于一般固定效应模型类实证研究的不同之处,从而拓展了关于固定效应模型实证研究的视野. 当然,需结合前文的研究结论设定αi的形式:第一,参照αi与各解释变量相关;第二,遵循超越对数成本函数的基本特征. 最终得到了上文αi的形式.
在式(1)中,αi与各解释变量的相关性是通过食品安全变量与这些变量之间的交互来实现的,这与Gertler和Waldman[15]、王志刚等[23]的研究是相似的,但Antle[17]却对αi的形式作了一些微调,而Mocan[24]则对αi作了更为灵活的变换. 这表明可以根据研究的需要来灵活设定式αi的形式,至于如何设定还需要另外进行相关的专题研究.
2.1. 稳健标准差检验
2.2. POOL与FE检验
2.3. POOL与RE检验
2.4. FE与RE检验
2.5. FE模型的另类表达
-
从上文的推导过程来看,要素成本份额方程式(2)由超越对数成本面板方程式(1)分别对各种要素价格求偏微分得出,即前者为后者的一部分,因此,可将式(1)看作“母方程”,而将式(2)看作其“子方程”. 在此计量分析过程中,经过多次实验发现,减轻要素成本份额方程的多重共线性将有助于缓解超越对数成本面板方程的多重共线性问题,进而将缓解由两者组成的系统结构模型的多重共线性. 为此,归纳出以下结论:
假定A方程为“母方程”、B方程为“子方程”,那么减轻B方程的多重共线性将有助于缓解A方程的多重共线性问题,进而缓解由A方程和B方程构成的系统结构模型的多重共线性.
该结论对于实证分析中减轻此类多重共线性问题提供了重要思路. 在实证分析中,相较而言,“母方程”的结构要比“子方程”的结构复杂得多,这意味着通过“子方程”解释变量的多重共线性分析可以研判“母方程”解释变量的多重共线性问题,从而简化了分析. 因此,我们将该问题转化为对式(2)进行多重共线性处理. 将食品安全方程式(3)带入式(2),得到简化形式:
其中,τl=εl+γlsζit. 式(4)各解释变量之间的相关系数矩阵见表 1.
从表 1可以看出,lnY与lnWm之间的相关系数高达0.961 7,出现了严重的多重共线性. 经过多次实验,变换Wm的形式. 在对式(4)多重共线性问题的处理过程中发现了另外一个问题,即变量lnKit和lnQit的系数估计值出现了参数线性表达的形式,而这种形式对于参数求解造成了很大的困扰,很难求解出各个参数,导致系统结构模型难以识别(Identification). 进一步观察发现,要解出系统结构模型的各个参数,要求式(4)的参数表达式只能以“乘积”的形式出现,即需要对式(4)中的两个线性参数表达式进行“拆分”. 以此为逻辑起点,采取“逆推法”,意味着在将式(3)代入式(1)的过程中,两个式子相同变量K和Q不能采取同样的形式(对数形式),为了与变量Wm形式变化取得一致性,将变换式(3)中K和Q原本的对数形式.
从上述分析可以看出,在对多重共线性问题的处理过程中还“掺杂”了方程的可识别问题,从而使问题变得更为复杂,因此,需要将二者同时结合起来考虑.
-
为了同时考虑两个问题(可识别问题、多重共线性问题),我们再次聚焦食品安全方程式(3),并对其中的Wm、K和Q三个变量进行形式变换. 对数据进行转换时可采用两种技术:BOX-COX转换和幂阶梯转换,这两种转换能使数据更接近于正态分布,其中,自然对数为幂阶梯转换的一种或BOX-COX转换,其效果是为了减少数据的正偏态分布[25]. 从这个意义上讲,式(1)和(3)本质上相当于是对各变量进行幂阶梯转换或BOX-COX转换.
-
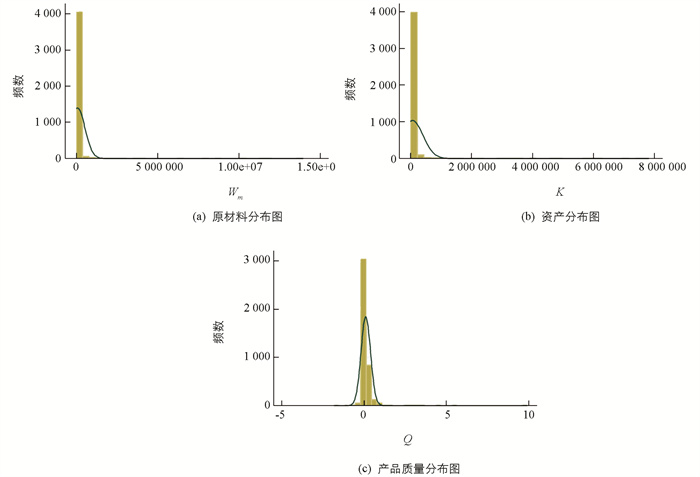
在转换之前,需对数据的分布进行考察,以便采取合适的方法进行转换,结果见图 1.
从图 1可以清晰地看出,变量Wm和K存在严重正偏态,但变量Q所呈现出的正偏态分布并不是那么严重. 这是因为,从对产品质量这一变量的处理来看(见上文的分析),Q为一中性变量(比例性指标),各观测值之间的数据差异本身就比较小. 为此,先对这三个变量采取BOX-COX转换,转换后的变量分别表示为BWm、BK和BQ,其相关统计量见表 2.
从表 2可以看出,BWm、BK和BQ变量的偏度统计量近似于0,这说明Wm、K和Q进行BOX-COX转换以后均呈现正态分布. 这样,我们达到了数据转换的目的,而且系统结构模型的可识别问题也得到了解决. 在此基础上,进一步考察转换以后各解释变量的多重共线性问题. 根据运行结果,进行BOX-COX转换之后,Y与Wm的相关系数似乎并没有降低多少,依然高达0.960 3. 而在对式(4)的两个线性参数表达式进行“拆分”之后,反而还增加了两类严重多重共线性:lnK与BK的相关系数为0.995 7(几乎完全相关);lnQ与BQ的相关系数为0.987 2. 这表明BOX-COX转换与变量取自然对数的情况比较接近,因此,从多重共线性这一视角来看,不能对Wm、K和Q进行BOX-COX转换,所以,转而对其进行幂阶梯转换.
-
在转换过程中,首先需要明确的是,只要对式(3)中Wm、K和Q不采取自然对数形式,便可以解决系统结构模型的可识别问题. 在这一前提下,对这三个变量进行幂阶梯转换以便处理多重共线性的问题,需要延伸为同时考量减轻多重共线性问题与数据的正态分布,而二者总是难以兼顾. 因此,需要进一步厘清一个基本事实:为了减轻严重多重共线性,只能“稍微”牺牲一下数据的正态分布;但也不能过分牺牲这一点,否则数据的严重偏态分布可能会对计量结果产生较大影响. 经过实验,最终得到了上文的式(3).
4.1. BOX-COX转换
4.2. 幂阶梯转换
-
经过对多重共线性和系统结构模型的可识别问题处理以后,将式(3)代入方程(1)和(2),通过计算整理,便得到食品安全内生时的系统简化模型,即为最终估计的模型. 利用2004-2007年肉制品面板数据,采用面板似不相关(Seemingly Unrelated Regression Estimation,简记SURE)迭代回归和最小距离估计(Minimum Distance Estimation,简记MDE)进行估计.
为了对结果进行对比分析,将食品安全外生(式(1)和(2)中不存在食品安全变量)时的估计结果作为基准(Bench Mark),以便考察加入食品安全变量后,估计结果会发生怎样的变化,从而更好地了解肉制品企业食品安全生产的行为. 当然,为何不能采用OLS估计系统简化模型,这需要考察各观测值扰动项之间是否存在相关性,为此,列出了经过面板SURE迭代回归后的“残差相关系数矩阵”(Correlation Matrix of Residuals),见表 3.
需要检验的原假设和备择假设分别为,H0:不存在组间截面相关,H1:存在组间截面相关. 一方面,如果原假设成立,意味着根据残差计算的个体扰动项之间的相关系数应接近于0,即在表 3的残差相关系数矩阵中,非主对角线的元素应离0不远. 而从上表可以看出,非主对角线的元素不全为0,这意味着原假设并不成立. 另一方面,从Breusch-Pagan LM统计量来看,在食品安全外生和内生情况下,p=0.000 0<0.01,也显著拒绝原假设,这说明系统模型的扰动项确实存在组间截面相关,表征使用SURE比单一方程的OLS更有效率(食品安全外生时的情况类似).
食品安全内生时的系统简化模型一共迭代了15次,并最终收敛于9.591e-07,估计结果见表 4.
在表 4中,第(1)列至第(4)列分别代表2004-2007年式(1)存在食品安全变量的简化形式各年度的回归结果. 可以看出,食品安全内生时系统简化模型的拟合优度比食品安全外生时系统简化模型的拟合优度(2004-2007年分别为0.228、0.204、0.157、0.141)有了较大改善,表征前者对数据的拟合程度要优于后者,这说明将食品安全变量纳入模型中是比较理想的选择.
-
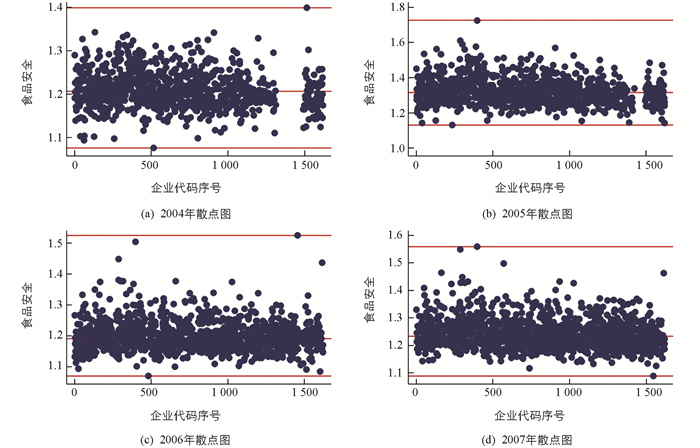
本文模拟出了2004-2007年的肉制品企业食品安全数据,让我们对食品安全有一个初步的感知,见图 2.
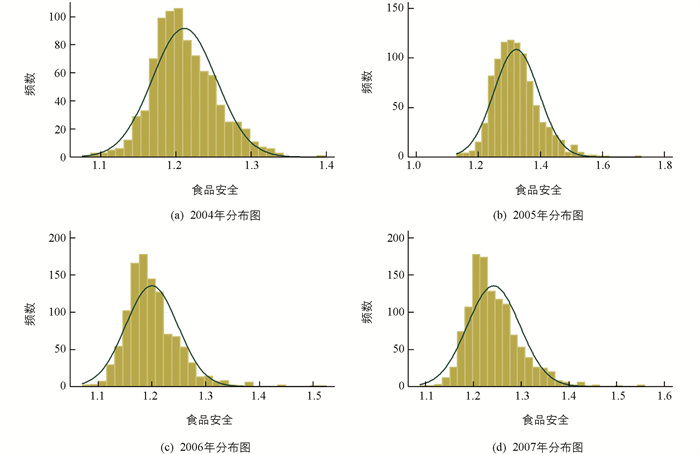
从图 2可以看出,2004-2007年各企业的食品安全水平比较集中,而且大约集中在1与1.8之间. 为了剔除异端值的影响,我们以中位数来代表各年度食品安全的平均水平,这也就反映了肉制品行业的食品安全水平:2004-2007年中国肉制品行业的食品安全平均水平分别为1.206 2、1.314 5、1.191 8和1.232 7. 图 3描绘出了2004-2007年度肉制品的食品安全水平的分布状况.
从图 3可以看出,2004-2007年肉制品企业的食品安全大致呈正态分布,这可以研判本文所模拟的食品安全数据具有合理性. 从现有研究来看,我们对这一数据的认知还非常有限. 这也不足为奇,正如劳动经济在研究工资时,对“能力”这一变量的控制,也是用“智商”(Intelligence Quotient,简称IQ)数据来捕捉的;或者如同产品质量一样,也是一个没有单位的中性变量. 因此,随着对食品安全的深入研究,将会揭示出更多关于食品安全的相关信息. 但有一点是可以肯定的:本文所模拟的食品安全数据正是基于特定行业(肉制品)的数据结构(2004-2007年面板数据)、并通过相应计量手段(面板SURE迭代估计)予以实现,这对当前关于食品安全指数的研究[26]可提供一定借鉴.
各分图中,最上面和最下面的水平线分别为最大值线和最小值线,中间的水平线为中位数线.
5.1. 简化模型估计
5.2. 食品安全数据模拟
-
从上述实证分析本文得出:
第一,模型形式选择. 通过模型形式的检验结果来看,拓展后的质量调整成本模型仍然为固定效应模型,属于面板模型实证研究的常见现象,表明对该模型的拓展仍然是科学、合理的. 而FE模型常见的表达方式是采取离差形式,将无法观测到的扰动项消除,以解决估计的一致性问题;如果按照此方法,那么考虑无法观测的食品安全变量的实证研究便无法进行下去. 可能目前的文献并未考虑到这一点,只是将精力集中在思考如何将食品安全变量表达出来. 但本文将这一问题有效纳入了面板模型的分析框架之中,既拓展了固定效应模型的相关研究,也让方程的设定变得更有说服力,这应该是本文的一个贡献.
第二,严重多重共线性和模型可识别处理. 从幂阶梯转换和BOX-COX转换视角,对超越对数成本面板方程进行了再认识. 以解释变量数据正态分布的改善为前提进行BOX-COX转换,虽然该方法解决了模型识别问题,但却未缓解严重多重共线性问题. 而幂阶梯转换的基本逻辑为随着变量形式的变换(变量幂指数的变化),该变量与其他变量之间的相关系数会发生相应的改变(多重共线性);同时,变化后变量的数据分布是否接近于正态分布,这需要在二者之间作出有效的权衡. 最终以缓解严重多重共线性为前提(首先要解决模型的识别问题),通过数据接近正态分布时所对应的变量进行重复实验,达到合理解决问题的目的.
第三,模型的优良性和对食品安全水平数据的认识. 从估计结果来看,食品安全内生时的模型比外生时的模型对样本数据拟合得更好,因此,在实证研究中如果不考虑食品安全变量,将会导致模型的有偏估计,结论也就失去可信性,最终提出的对食品安全问题监管的措施可能会出现偏差. 而且通过模型成功模拟出了食品安全水平的数据,让这一无法观测到的变量具体化,并且具有良好的分布.
第四,现有文献关于超对数成本函数的研究主要采用截面数据,而本文对其设定为面板模型进行分析,这为后续运用该函数展开面板数据分析奠定了基础. 同时,在设定过程中考虑了无法观察到的变量,这将对如何处理不可观测变量模型设定的实证研究起到推动作用. 本文对食品安全数据的模拟具有一定的应用价值,这将有助于开发测度企业食品安全水平的相关软件,一旦该软件对接企业的财务报表数据和国家居民收入数据等数据库,便可迅速掌握企业的食品安全水平,从而极大减轻政府相关部门对企业食品安全水平检测的压力.



 下载:
下载: