高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

穴式苗-肥同施水稻侧深施肥装置设计与试验

,  ,  ,  ,  , 

上一篇

下一篇

董晓威, 黄法伟, 刘俊兵, 等. 穴式苗-肥同施水稻侧深施肥装置设计与试验[J]. 西南大学学报（自然科学版）, 2023, 45(3): 58-73. doi: 10.13718/j.cnki.xdzk.2023.03.005
引用本文: 董晓威, 黄法伟, 刘俊兵, 等. 穴式苗-肥同施水稻侧深施肥装置设计与试验[J]. 西南大学学报（自然科学版）, 2023, 45(3): 58-73. doi: 10.13718/j.cnki.xdzk.2023.03.005
shu
DONG Xiaowei, HUANG Fawei, LIU Junbing, et al. Design and Experiment of Rice Deep-Side Fertilization Device for Hole-Type Seedling and Fertilizer Application[J]. Journal of Southwest University Natural Science Edition, 2023, 45(3): 58-73. doi: 10.13718/j.cnki.xdzk.2023.03.005
Citation: DONG Xiaowei, HUANG Fawei, LIU Junbing, et al. Design and Experiment of Rice Deep-Side Fertilization Device for Hole-Type Seedling and Fertilizer Application[J]. Journal of Southwest University Natural Science Edition, 2023, 45(3): 58-73. doi: 10.13718/j.cnki.xdzk.2023.03.005
shu

穴式苗-肥同施水稻侧深施肥装置设计与试验

  • 1.

    黑龙江八一农垦大学 工程学院，黑龙江 大庆 163319

  • 2.

    鸡西市农业综合技术中心，黑龙江 鸡西 158100

  • 3.

    黑龙江八一农垦大学 信息与电气学院，黑龙江 大庆 163319

  • 4.

    哈尔滨市农业科学院，哈尔滨 150028

  • 5.

    农业农村部农产品及加工品质量监督检验测试中心，黑龙江 大庆 163319

  • 基金项目: 黑龙江省博士后面上资助项目(LBH-Z20203); 中央引导地方科技发展专项(ZY20805); 黑龙江八一农垦大学学成人才科研启动计划(XDB202002); 黑龙江八一农垦大学“三纵”基础培育项目(ZRCPY202104)
详细信息
    作者简介:

    董晓威，博士，副教授，硕士研究生导师，主要从事水田生产全程机械化技术与装备研究 .

    通讯作者: 衣淑娟，教授，博士研究生导师

  • 中图分类号: S224.21

Design and Experiment of Rice Deep-Side Fertilization Device for Hole-Type Seedling and Fertilizer Application

  • 1.

    School of Engineering, Heilongjiang Bayi Agricultural University, Daqing Heilongjiang 163319, China

  • 2.

    Jixi Comprehensive Agricultural Technology Center, Jixi Heilongjiang 158100, China

  • 3.

    College of Information and Electrical Engineering, Heilongjiang Bayi Agricultural University, Daqing Heilongjiang 163319, China

  • 4.

    Harbin Academy of Agricultural Science, Haerbin 150028, China

  • 5.

    Inspection and Test Center of Agricultural products and processed products of quality supervision (Daqing), Ministry of Agriculture and Rural Affairs, Daqing Heilongjiang 163319, China

  • 摘要: 为解决水稻侧深施肥作业相邻秧苗间化肥利用率低的问题，结合穴施肥农艺方法，设计了间歇定点穴式水稻侧深施肥装置. 该装置采用垂直螺旋搅龙强排固体颗粒肥，依据预设的插秧与施肥动作之间的延时，控制步进电机的启停实现间歇的排肥动作，进一步控制螺旋搅龙的旋转角度，从而保证定点精量排肥. 应用EDEM软件对穴式水稻侧深施肥装置进行仿真试验及分析，以行进速度、排肥能力、施肥高度为试验因素，以施肥位置合格率和排肥稳定性为响应指标，对装置排肥性能进行三因素五水平正交旋转组合试验，并使用Design-Expert软件对试验结果进行方差分析和响应面分析，获得最优解为行进速度0.47 m/s、排肥能力2.69 g/r、施肥高度16.7 mm，施肥位置合格率93.02%和排肥稳定性6.52%. 以最优解为试验参数进行台架试验，验证得到施肥位置的合格率为91.23%和排肥稳定性为7.15%，与优化结果基本一致，满足穴式水稻侧深施肥的农艺要求.
    Abstract: To resolve the problem of low efficiency of fertilizer utilization between adjacent seedlings in rice deep-side fertilization, combined with agronomic method of hole-type fertilization, an intermittent fixed-point precise hole-type deep-side fertilization device was designed. The device uses a vertical spiral auger to force the release of solid fertilizer. This is realized with a stepper motor, in which the start and stop is controlled by setting a delay period between transplanting and fertilizing to realize intermittent fertilizer discharge, and the rotation angle of the auger is then controlled to ensure to discharge a precise amount of fertilizer. The simulation experiment was performed using the EDEM software to analyze the performance of the device. Herein, the traveling speed (m/s), fertilizer discharge capacity (g/r) and fertilizing height (mm) were treated as the experimental factors. The accuracy of fertilization point and the stability of fertilizer discharge were regarded as the response indicators. A three-factor five-level orthogonal rotation combination experiment was adopted to test the fertilizer discharge performance of the designed device. The Design-Expert software was used to perform the variance analysis and response surface analysis. The results were summarized as below. The optimal solutions were that the accuracy of fertilization point was calculated to be 93.02%, and the stability of fertilization was 6.52%. When the traveling speed was 0.47 m/s, the fertilizer discharge capacity was 2.69 g/r, and the fertilizing height was 16.7 mm. The bench test was conducted using the optimal parameters. The verified accuracy of fertilization point was 91.23%, and stability of fertilization was 7.15 %, which were consistent with the simulation results. This can satisfy the agronomic requirements of hole-type fertilization in rice planting.
  • 加载中

  • 图 1  试验装置结构

    下载: 全尺寸图片 幻灯片

    图 2  螺旋排肥部件坐标系的建立

    下载: 全尺寸图片 幻灯片

    图 3  颗粒肥进入螺旋槽之前的受力分析

    下载: 全尺寸图片 幻灯片

    图 4  插秧机构工作原理图

    下载: 全尺寸图片 幻灯片

    图 5  控制系统原理

    下载: 全尺寸图片 幻灯片

    图 6  主程序片段

    下载: 全尺寸图片 幻灯片

    图 7  人机交互界面

    下载: 全尺寸图片 幻灯片

    图 8  仿真界面总览

    下载: 全尺寸图片 幻灯片

    图 9  仿真详细过程

    下载: 全尺寸图片 幻灯片

    图 10  化肥质量流量仿真图

    下载: 全尺寸图片 幻灯片

    图 11  试验台实物图

    下载: 全尺寸图片 幻灯片

    图 12  响应曲面分析图

    下载: 全尺寸图片 幻灯片

    表 1  控制系统组成表

    名称 型号
    PLC 西门子S7200ST20，24 V，DC供电，12DI /8 DO
    触摸屏 昆仑通态TPC-7062TX，24 V，DC供电
    步进电机 普菲德86BYG250H，转矩12 N·m
    插秧电机 可调速，60 W，350 r/min
    行进电机 可调速，100 W，150 r/min
    步进驱动器 普菲德DMA860H，24 V，DC供电
    传感器 菲尔斯特BRW600-400A，24 V，DC供电
    下载: 导出CSV

    表 2  仿真参数

    项目名称 属性 数值
    密度/(kg·m-3) 化肥 1 552
    Q235 7 850
    泊松比 化肥 0.25
    Q235 0.35
    弹性模量/GPa 化肥 0.096
    Q235 210
    静摩擦系数 化肥颗粒与化肥颗粒 0.372
    化肥颗粒与Q235 0.361
    滑动摩擦系数 化肥颗粒与化肥颗粒 0.378
    化肥颗粒与Q235 0.382
    碰撞恢复系数 化肥颗粒与化肥颗粒 0.075
    化肥颗粒与Q235 0.421
    下载: 导出CSV

    表 3  因素水平编码表

    因素水平 行进速度x1/(m·s-1) 排肥能力x2/(g·r-1) 施肥高度x3/mm
    1.682 0.69 5.52 41.82
    1 0.60 4.5 35
    0 0.47 3.0 25
    -1 0.35 1.5 15
    -1.682 0.26 0.48 8.18
    下载: 导出CSV

    表 4  试验方案与结果

    试验序号 行进速度 排肥能力 施肥高度 施肥位置合格率(y1)/% 排肥稳定性(y2)/%
    1 -1 -1 -1 95.02 16.2
    2 1 -1 -1 95.12 14.6
    3 -1 1 -1 90.69 14.7
    4 1 1 -1 95.07 10.2
    5 -1 -1 1 90.21 14.6
    6 1 -1 1 94.79 10.9
    7 -1 1 1 86.80 10.2
    8 1 1 1 90.68 6.4
    9 -1.682 0 0 88.48 15.5
    10 1.682 0 0 96.60 8.2
    11 0 -1.682 0 96.35 15.7
    12 0 1.682 0 88.71 8.0
    13 0 0 -1.682 96.49 15.8
    14 0 0 1.682 88.26 8.2
    15 0 0 0 92.52 12.2
    16 0 0 0 92.24 11.9
    17 0 0 0 92.62 12.9
    18 0 0 0 92.52 12.8
    19 0 0 0 92.52 12.5
    20 0 0 0 92.72 13.0
    21 0 0 0 92.32 12.8
    22 0 0 0 92.20 12.7
    23 0 0 0 91.89 12.4
    下载: 导出CSV

    表 5  施肥位置合格率方差分析

    来源 平方和 自由度 均方 F p
    x1 83.69 1 83.69 54.86 ＜0.000 1***
    x2 4.81 1 4.81 3.15 0.099 3*
    x3 51.60 1 51.60 33.83 ＜0.000 1***
    x1x2 0.000 5 1 0.000 5 0.000 3 0.113 0
    x1x3 1.81 1 1.81 1.19 0.042*
    x2x3 0.73 1 0.73 0.48 0.102 4
    x12 13.53 1 13.53 8.87 0.010 7**
    x22 6.47 1 6.47 4.24 0.060 1*
    x32 10.41 1 10.41 6.83 0.021 5**
    模型 172.65 9 19.18 12.58 ＜0.000 1***
    残差 19.83 13 1.53
    失拟项 11.35 5 2.27 2.14 0.1618
    纯误差 8.48 8 1.06
    总和 192.48 22
    注：***表示差异极显著(p＜0.01); **表示差异显著(0.01＜p＜0.05); *表示差异较显著(0.05＜p＜0.1).
    下载: 导出CSV

    表 6  排肥稳定性方差分析

    来源 平方和 自由度 均方 F p
    x1 3.43 1 3.43 1.21 0.092 2*
    x2 0.072 1 0.072 0.025 0.676 2
    x3 33.11 1 33.11 11.63 0.004 6***
    x1x2 0.21 1 0.21 0.074 0.389 6
    x1x3 1.05 1 1.05 0.37 0.053 8*
    x2x3 1.71 1 1.71 0.60 0.052 0*
    x12 3.93 1 3.93 1.38 0.061 1*
    x22 25.65 1 25.65 9.01 0.010 2**
    x32 25.65 1 25.65 9.01 0.010 2**
    模型 94.73 9 10.53 3.70 0.016 5**
    残差 37.00 13 2.85
    失拟项 17.84 5 6.97 25.70 0.263 2
    纯误差 2.17 8 0.27
    总和 131.74 22
    注：***表示差异极显著(p＜0.01); **表示差异显著(0.01＜p＜0.05); *表示差异较显著(0.05＜p＜0.1).
    下载: 导出CSV

    表 7  试验因素对响应指标的贡献率

    响应指标 试验因素贡献率 贡献率排序
    x1 x2 x3
    y1 1.506 1.065 1.477 x1＞x3＞x2
    y2 0.312 0.445 1.359 x3＞x2＞x1
    下载: 导出CSV
  • [1] 陶玥玥, 金梅娟, 汤云龙, 等. 水生植物堆肥替代部分氮肥提高水稻产量与稻田土壤肥力[J]. 农业工程学报, 2017, 33(18): 196-202. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201718026.htm
    [2] 张璐, 黄晶, 高菊生, 等. 长期绿肥与氮肥减量配施对水稻产量和土壤养分含量的影响[J]. 农业工程学报, 2020, 36(5): 106-112. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU202005012.htm
    [3] 刘钦普, 孙景荣, 濮励杰. 中国及欧美主要国家化肥施用强度与综合效率比较研究[J]. 农业工程学报, 2020, 36(14): 9-16. doi: 10.11975/j.issn.1002-6819.2020.14.002
    [4] 方林发, 张宇亭, 谢军, 等. 氮肥用量和运筹对冷浸田水稻产量和氮素利用率的影响[J]. 西南大学学报(自然科学版), 2020, 42(3): 53-60. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2020.03.008
    [5] SU N, XU T S, SONG L T, et al. Variable Rate Fertilization System with Adjustable Active Feed-Roll Length[J]. International Journal of Agricultural & Biological Engineering, 2015, 8(4): 19-26.
    [6] 张国忠, 王洋, 刘浩蓬, 等. 离心侧抛式藕田撒肥器设计与试验[J]. 农业工程学报, 2021, 37(19): 37-47. doi: 10.11975/j.issn.1002-6819.2021.19.005
    [7] WANG J, LI S, ZHANG Z, et al. Design and Experiment of Electrical Drive-Side-Deep Hill-Drop Fertilization System for Precision Rice Hill-Direct-Seeding Machine[J]. Transactions of the CSAE, 2018, 34(8): 43-54.
    [8] 王金峰, 高观保, 翁武雄, 等. 水田侧深施肥装置关键部件设计与试验[J]. 农业机械学报, 2018, 49(6): 92-104. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX201806011.htm
    [9] 王金峰, 高观保, 王金武, 等. 叶片调节式水田侧深施肥装置设计与试验[J]. 农业机械学报, 2018, 49(3): 68-76. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX201803008.htm
    [10] 王金峰, 尚文虎, 翁武雄, 等. 圆盘顶出式水田侧深施肥装置设计与试验[J]. 农业机械学报, 2021, 52(6): 62-72. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX202106007.htm
    [11] 左兴健, 武广伟, 付卫强, 等. 风送式水稻侧深精准施肥装置的设计与试验[J]. 农业工程学报, 2016, 32(3): 14-21. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201603003.htm
    [12] 董俊汶, 汪洋, 赵进, 等. 条施机定量施肥控制系统设计[J]. 西南师范大学学报(自然科学版), 2019, 44(4): 93-99. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-XNZK201904017.htm
    [13] 陈长海, 许春林, 毕春辉, 等. 水稻插秧机侧深施肥技术及装置的研究[J]. 黑龙江八一农垦大学学报, 2012, 24(6): 10-12, 25. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-HLJK201206005.htm
    [14] 董晓威, 李伟凯, 衣淑娟, 等. 间歇定点精量水稻侧深施肥方法及装置的设计研究[J]. 黑龙江八一农垦大学学报, 2019, 31(3): 56-63. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-HLJK201903010.htm
    [15] 张俊雄, 刘华猛, 高金, 等. 玉米分层正位穴施肥精播机SPH仿真与试验[J]. 农业机械学报, 2018, 49(9): 66-72. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX201809007.htm
    [16] 万玲, 谢东波, 李杨, 等. 玉米行间滚轮式穴施排肥器设计与试验[J]. 农业机械学报, 2020, 51(11): 64-73. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX202011007.htm
    [17] 李红宇, 李逸, 赵海成, 等. 点深施肥对寒地水稻产量品质及氮肥利用率的影响[J]. 华北农学报, 2021, 36(1): 159-168. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-HBNB202101024.htm
    [18] 王紫玉, 梁春英, 王洪超, 等. 玉米变量穴施肥试验台的设计与试验[J]. 农机化研究, 2020, 42(4): 166-169, 174. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NJYJ202004033.htm
    [19] 刘正道, 王庆杰, 李洪文, 等. 耦合CFD-DEM的气力式种肥穴施装置投肥路径分析与试验[J]. 农业工程学报, 2019, 35(21): 18-25. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201921003.htm
    [20] 袁文胜, 李坤, 金诚谦, 等. 穴施肥排肥器设计与试验[J]. 农机化研究, 2018, 40(1): 145-149, 165. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NJYJ201801027.htm
    [21] 张勋, 朱瑞祥, 陈克克. 穴播穴施肥装置控制系统的设计[J]. 农机化研究, 2009, 31(4): 61-63. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NJYJ200904017.htm
    [22] 陈雄飞, 罗锡文, 王在满, 等. 水稻穴播同步侧位深施肥技术试验研究[J]. 农业工程学报, 2014, 30(16): 1-7. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201416001.htm
    [23] 董晓威. 垂直螺旋式水稻侧深施肥机理与装置参数研究[D]. 大庆: 黑龙江八一农垦大学, 2019.
    [24] 许春林, 单伊尹, 辛亮, 等. 探出开孔式高速水稻膜上插秧机分插机构设计与试验[J]. 农业机械学报, 2020, 51(5): 79-87. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX202005008.htm
    [25] 朱德泉, 熊玮, 蒋锐, 等. 2ZGK-6型可调宽窄行高速水稻插秧机设计与试验[J]. 农业工程学报, 2016, 32(21): 37-45. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201621005.htm
    [26] 陈海涛, 赵阳, 侯守印, 等. 同步膜上开孔插秧装置运动学仿真与参数优化试验[J]. 农业工程学报, 2016, 32(11): 25-30. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201611004.htm
  • 加载中
图( 12) 表( 7)
计量
  • 文章访问数:  4075
  • HTML全文浏览数:  4075
  • PDF下载数:  437
  • 施引文献:  0
出版历程
  • 收稿日期:  2022-06-08
  • 刊出日期:  2023-03-20

穴式苗-肥同施水稻侧深施肥装置设计与试验

    通讯作者: 衣淑娟，教授，博士研究生导师
    作者简介: 董晓威，博士，副教授，硕士研究生导师，主要从事水田生产全程机械化技术与装备研究
  • 1. 黑龙江八一农垦大学 工程学院，黑龙江 大庆 163319
  • 2. 鸡西市农业综合技术中心，黑龙江 鸡西 158100
  • 3. 黑龙江八一农垦大学 信息与电气学院，黑龙江 大庆 163319
  • 4. 哈尔滨市农业科学院，哈尔滨 150028
  • 5. 农业农村部农产品及加工品质量监督检验测试中心，黑龙江 大庆 163319
  • 收稿日期:  2022-06-08
基金项目:  黑龙江省博士后面上资助项目(LBH-Z20203); 中央引导地方科技发展专项(ZY20805); 黑龙江八一农垦大学学成人才科研启动计划(XDB202002); 黑龙江八一农垦大学“三纵”基础培育项目(ZRCPY202104)

摘要: 为解决水稻侧深施肥作业相邻秧苗间化肥利用率低的问题，结合穴施肥农艺方法，设计了间歇定点穴式水稻侧深施肥装置. 该装置采用垂直螺旋搅龙强排固体颗粒肥，依据预设的插秧与施肥动作之间的延时，控制步进电机的启停实现间歇的排肥动作，进一步控制螺旋搅龙的旋转角度，从而保证定点精量排肥. 应用EDEM软件对穴式水稻侧深施肥装置进行仿真试验及分析，以行进速度、排肥能力、施肥高度为试验因素，以施肥位置合格率和排肥稳定性为响应指标，对装置排肥性能进行三因素五水平正交旋转组合试验，并使用Design-Expert软件对试验结果进行方差分析和响应面分析，获得最优解为行进速度0.47 m/s、排肥能力2.69 g/r、施肥高度16.7 mm，施肥位置合格率93.02%和排肥稳定性6.52%. 以最优解为试验参数进行台架试验，验证得到施肥位置的合格率为91.23%和排肥稳定性为7.15%，与优化结果基本一致，满足穴式水稻侧深施肥的农艺要求.

English Abstract

    全文HTML

  • 开放科学(资源服务)标志码(OSID):

  • 水稻在我国每年粮食总产量中的占比一直在31%以上，在保证国家粮食安全方面发挥着重要作用. 而化肥的施用保证了水稻的高产与稳产，增产幅度高达50%[1]. 当前，我国水稻施肥多采用传统的人工撒播方式，存在施肥技术不规范、施肥均匀性差、施肥量较大、生产成本较高、肥料养分流失严重等问题，并对周围水系生态环境污染严重[2-3]. 随着水稻插秧机技术的更新以及水稻专用缓释肥的应用，使机插水稻侧深施肥技术得到广泛应用，降低了劳动成本，减少了肥料施用量，提高了肥料利用率[4-5].

    近年来，国内科研人员针对水田施肥装置及关键部件开展了大量研究. 张国忠等[6]设计了一种离心侧抛式撒肥器，通过建立的理论模型，确定了影响肥料颗粒运动特性的主要参数，并利用EDEM软件进行了单因素仿真试验与实际撒肥试验; WANG[7]和王金峰等[8-10]采用EDEM软件对水田施肥装置关键部件进行了设计与试验研究，获得肥料颗粒与排肥部件之间的运动模型，并利用Design-Expert软件对各影响因素进行了优化及验证试验; 左兴健等[11]针对乘坐式插秧机设计了风送式水稻侧深精准施肥装置，并开展风送排肥理论和水田侧深精准施肥控制方法的研究; 董俊汶等[12]针对化肥利用率低、肥料浪费严重和精量施肥实施难度较大的问题，设计了条施机定量施肥控制系统，试验证明其控制精度较好; 陈长海等[13]对水稻螺旋搅龙式侧深施肥装置开展的设计与试验研究，提高了施肥稳定性和均匀性，解决了气力式排肥装置的倒灌、拥堵问题. 上述学者研究的水田施肥装置施肥方式大多为连续的条播施肥形式.

    资料表明，穴施肥技术可进一步降低肥料施肥量，提高肥料利用率，同时减少生态污染[14-17]. 王紫玉等[18]设计了变量穴施肥试验台，在外槽轮排肥器的基础上，通过控制排肥口挡片实现穴施肥，配合排种器监测装置实现了种-肥同步施用; 刘正道等[19]设计了一种用于颗粒状肥料穴式施用的腔盘式精量穴施肥装置，可实现精量稳定取肥和低位快速投肥; 袁文胜等[20]设计了一种勺轮式穴施肥排肥器，通过勺轮、盛肥盘及隔板等部件的配合，使排出的颗粒肥料成穴; 张勋等[21]设计了穴施肥装置，在窝眼轮式排肥装置基础上增加化肥二次定位机构，实现穴施肥控制功能. 陈雄飞等[22]在同步开沟起垄水稻精量穴播技术的基础上，提出了一种水稻穴播同步侧位深施肥技术，试验表明该技术具有增产和节约成本的效用，但此种模式适用于水稻直播种植农艺. 国内学者研制的穴式排肥机构及施肥装置主要用于旱田作物的施肥作业，大多不适用水稻机插作业环境.

    本文结合穴式精量水稻侧深施肥技术[14]，设计一种间歇穴式精量水稻侧深施肥装置，采用垂直螺旋作为排肥部件，通过建立螺旋排肥过程中肥料颗粒的运动模型，分析影响装置排肥性能指标的关键因素，通过EDEM仿真分析及台架试验，确定穴式施肥装置最佳结构和工作参数，实现水稻穴式精量施肥，降低肥料的施用量，促进减施增效.

1.   结构设计与工作过程分析

    1.1.   结构及工作原理

    1.1.1.   结构

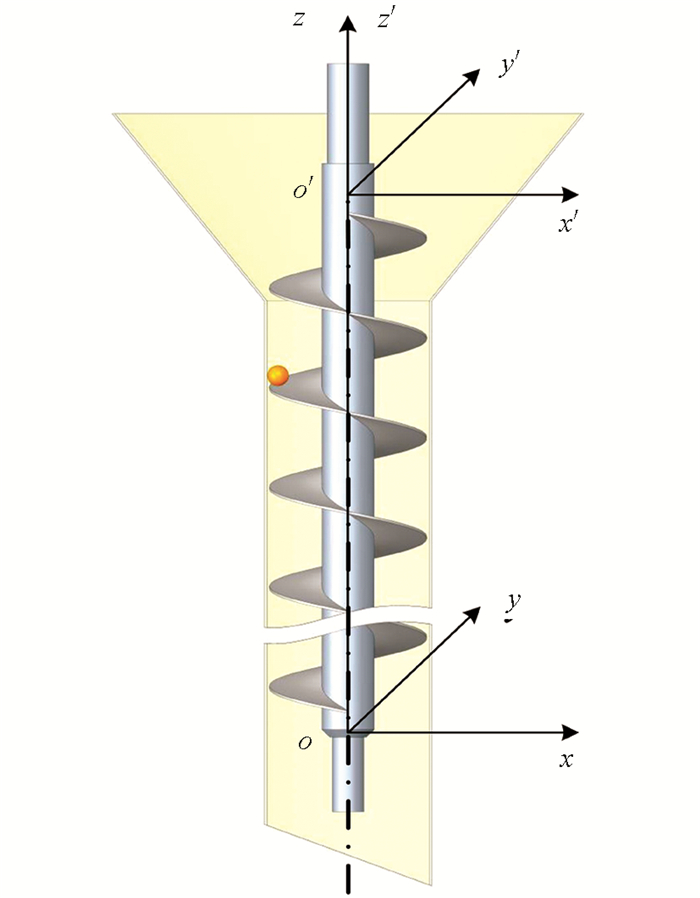
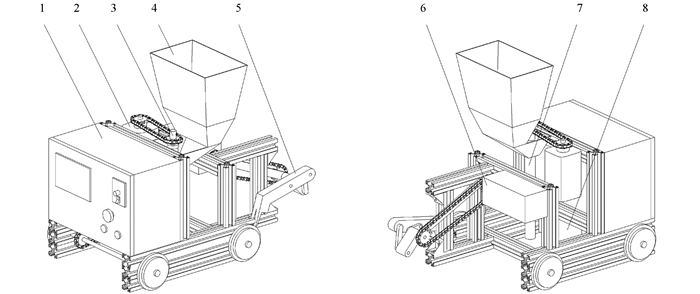
  • 穴式精量水稻侧深施肥装置主要由行走机构、插秧机构、施肥机构、动力传动系统、控制系统等组成，如图 1所示. 行走系统主要由行进减速电机、齿轮链条传动系统以及行走轮构成; 插秧机构主要由插秧减速电机、齿轮链条传动系统以及曲柄连杆机构构成; 施肥机构主要由步进电机、齿轮链条传动系统以及肥箱系统构成; 控制系统主要由PLC、触摸屏、步进电机驱动器构成.

    其中，行走系统实现施肥装置的行进运动，插秧机构用于完成插秧作业，控制系统除了控制垂直排肥螺旋的间歇运动，还控制施肥机构与插秧机构的联动，使苗-肥位置满足穴式水稻侧深施肥的农艺要求.

    • 1.1.2.   工作原理

  • 在PLC控制箱设定施肥装置的行进速度、插秧速度、螺旋转速与延时时间后，启动步进电机，化肥填充螺旋搅龙与排肥护管形成的储肥空间，随后启动行进减速电机、插秧减速电机及排肥步进电机，装置整体做匀速直线运动，插秧爪每进行一次插秧动作，传感器就捕捉一次信号，并将信号传入控制箱中，经过延时后，步进电机按设定的转速与转角运转，从而带动垂直螺旋搅龙完成排肥动作.

    • 1.2.   排肥关键部件参数设计

  • 排肥部件主要由肥料箱、螺旋搅龙、排肥护管及传动系统等组成，由步进电机输出轴通过传动链驱动搅龙转动完成排肥动作，并将肥料颗粒施于水稻秧苗侧3~4 cm、深4~5 cm位置处，螺旋搅龙排肥器的内外径、螺距、转速等参数直接影响排肥稳定性[14]，相关参数的取值范围可通过式(1)和式(2)来确定.

    式中：R为螺旋轴半径，mm; D为螺旋轴直径，mm; ψ为化肥填充系数，取0.9; C为螺旋倾角系数，取0.46; ρ为化肥密度，取1 552 kg/m3; K为物料综合特性系数，取0.063 2; Q为目标排肥量，取26.65 kg/h.

    由式(1)确定搅龙外径(D)可选参数为17，19，21，23，25 mm; 由式(2)确定搅龙的工作转速可选参数为170，180，190，200，220 r/min; 螺旋轴内径d为(0.2~0.35) D，可得d为5~9 mm; 螺旋搅龙螺距S=0.9×D，得S为15.3~22.5 mm.

    • 1.3.   排肥过程理论分析

  • 假设排肥部件结构参数已定，且螺旋外径与排肥护管间隙小于最小肥料颗粒的直径，肥料箱充入足量肥料颗粒后，肥料颗粒将充满肥箱及其内置的螺旋槽. 以肥料颗粒和螺旋排肥部件为研究对象，其将受到重力、螺旋推力、颗粒间作用力和摩擦力等，肥料颗粒流将以拟流体形式在螺旋槽内进行运动[23].

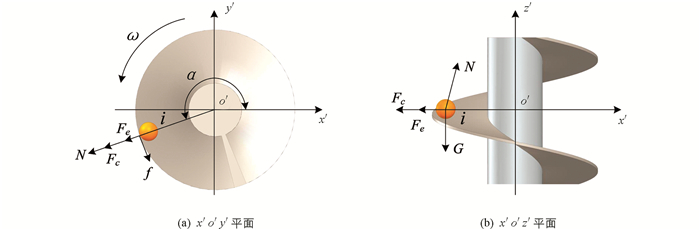
    当排肥开始，随着步进电机的间歇启动，在螺旋强制推动下，肥料颗粒将会依次进入下一个螺旋槽内，同时螺旋外径轮廓附近的肥料颗粒将会在相互作用力下涌向螺旋槽. 当螺旋处于匀速转动时，螺旋槽的充肥过程连续且时间长; 当螺旋处于间歇转动时，启停瞬间的转速变化较大，充肥过程间断且时间短. 以螺旋排肥护管建立定参考系oxyz，以转动的螺旋轴建立动参考系o′x′y′z′，排肥护管和排肥螺旋轴的轴线为z轴和z′轴方向，且两者重合，如图 2所示.

    忽略肥料颗粒流中相邻颗粒间的相互作用，选取任意肥料颗粒i为研究对象. 假定某一时刻t肥料颗粒i刚刚进入螺旋外径的轮廓，沿螺旋面相对滑动，且肥料颗粒i的速度与螺旋轴外径轮廓的线速度相同，对t时刻的肥料颗粒i进行受力分析，如图 3所示.

    此时，肥料颗粒i所受的力有重力G、滑动摩擦力f、螺旋面的支撑力N、牵连惯性力Fe和科氏力Fc，则颗粒i的动力学方程为

    式中：f=μN，Fe=miωi2ri，Fc=2miωvrel. mi为肥料颗粒的质量，kg; ω为螺旋的角速度，rad/s; ri为肥料颗粒质心所在半径，m; μ为肥料颗粒与螺旋间的摩擦因数，vrel为肥料颗粒沿螺旋外缘相对速度，m/s; ωi为肥料颗粒沿螺旋外径轮廓的相对角速度，rad/s.

    如果考虑其它肥料颗粒和螺旋外径轮廓对颗粒i的作用，此时颗粒i的角速度ωi很小，则Fe可以忽略不计. 因此，颗粒i此时相对运动轨迹的法线加速度arn和切线加速度art为

    式中：α为肥料颗粒i质心所处螺旋面的螺旋升角，(°).

    如果要使螺旋槽能正常充肥，此时肥料颗粒i只能沿着螺旋面做相对滑动，art=dvrel/dt=d2srel/dt2，即arn=0，则式(4)变换可得

    且颗粒i的绝对速度va、螺旋面外缘切向速度ve、颗粒i沿螺旋面外缘相对速度vrel满足如下关系

    式中：va＞vrel，va与ve同向. 肥料颗粒i沿螺旋面外缘以相对速度vrel开始滑动，在后续其它颗粒和螺旋面的作用下逐渐进入下一个螺距段，进而顺利完成充肥过程. 由式(5)可知，肥料颗粒的充肥过程与螺旋的角速度ω(或螺旋转速n)、螺旋外径R(即ri)、螺旋角α(或节距S)相关.

    • 1.4.   插秧点与施肥点耦合分析

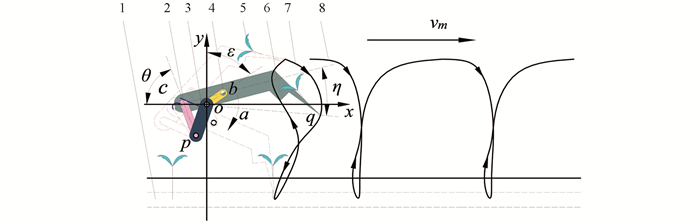
  • 插秧机构主要由曲柄、摇杆、栽植臂等组成，曲柄与摇杆通过轴承铰接于机架，由插秧减速电机提供动力，驱动摇杆与栽植臂做往复运动，使秧针实现如图 4所示的复杂平面运动. 当秧针到达轨迹的最低点，凸轮与拨叉分离，推秧器在推秧弹簧的作用下，实现一次快速插秧作业[24-26]，此刻以秧针轨迹到达的最低点为中心，以半径R为3~4 cm确定施肥点位置，并保证排肥螺旋完成排肥动作，然后凸轮再将推秧器复位，准备重复下一次插秧及穴式排肥作业.

    如图 4所示，秧爪的运动轨迹直接影响实际插秧作业时秧苗的插植位置. 以曲柄旋转中心o为原点，建立平面直角坐标系，曲柄按照图示以角速度为a做顺时针匀速圆周运动. 其中曲柄(ob)、机架(op)、摇杆(pc)、栽植臂(cb)的长度分别为l1，l2，l3，l4; o，p，b三点坐标分别为(0，0)，(xp，yp)，(l1sin at，l1cos at); op两点间沿x，y方向的距离绝对值分别为xop，yop; 角θ，ε，η分别为摇杆pc与x轴负方向间夹角、曲柄与y轴正方向间夹角、秧针与栽植臂由装配关系所产生的夹角，时间用T表示.

    建立矢量方程

    运用消参法求解式(7)，可得到点q静态坐标为(xop+l3sin θ，yop+l3cos θ)，由平面两点距离公式得

    在实际作业中，试验装置还具有水平行进速度vm，则q点的动态坐标为[l1cos η+l4cos(ε+η)+vmT，l4sin(ε+η)-l1sin η]，动点q的轨迹方程、速度方程、加速度方程分别为式(9)、式(10)、式(11).

    通过建立的数学模型，获得了图 4中的秧爪运动轨迹，验证了插秧机构的秧爪运动轨迹满足插秧与穴施肥的试验要求.

    • 1.5.   控制系统设计

  • 控制系统主要完成垂直螺旋的间歇排肥运动以及施肥机构与插秧机构的联动耦合控制. 根据插秧株距l，m; 每穴施肥量B，g; 单圈排肥量P，g/r; 施肥装置的行进速度v，m/s; 苗-肥纵向距离f，取值为0.02 m，延时时间t由式(12)得到，由式(13)求得每一次穴施肥动作PLC所需要发送的脉冲数M. 在步进电机驱动器上选择适当的细分X来控制步进电机的转速，细分X由式(14)计算得到.

    式中：Δt=2f/v，T=l/v，B=n·P. t为延时时间，s; T为插秧周期，s; W为PLC的脉冲频率; G为步进电机的步距角，(°); X为步进电机驱动器细分数目; M为每次穴施肥发送的脉冲数; Δt为每次穴施肥的排肥时间，s; n为每次穴施肥螺旋旋转的圈数，r.

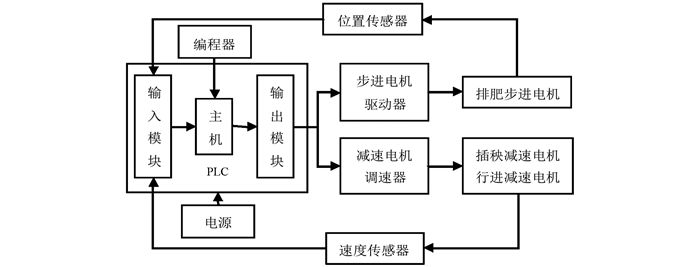
    穴施肥试验装置控制系统原理如图 5所示. PLC读取通过输入模块(触摸屏)设定的速度参数、施肥参数以及延时时间等作业参数，系统根据获取的参数来控制施肥装置完成行进动作和插秧动作，同时控制穴施肥位置与每次施肥量. 在控制施肥位置与穴施肥量时，当金属材质的秧针经过传感器探测范围内时，传感器内的常开开关闭合，连接传感器与PLC之间的电路由低电平变为高电平，秧针离开传感器的探测范围后，传感器内的常开开关又转为常开状态，这个过程中由电平的变化而产生的信号传至PLC，PLC经过延时时间t后，经步进电机驱动器向排肥步进电机发送细分后的M个脉冲，由步进电机经传动机构驱动排肥螺旋完成排肥动作，从而实现对排肥位置的控制. 通过调整步距角的大小来实现每穴的精量排肥控制.

    其中，电机转速由驱动器进行调节，且延时时间t可调，电机速度输出由系统程序进行控制. PLC的控制量主要包括两个脉冲输出接口和一个模拟输出接口，脉冲输出接口控制插秧减速电机和施肥步进电机，模拟输出接口控制行进减速电机; 输入量主要包括3个脉冲输入接口，负责检测试验台和垂直螺旋的工作速度以及输入插秧信号，控制系统的主要组成部分如表 1所示.

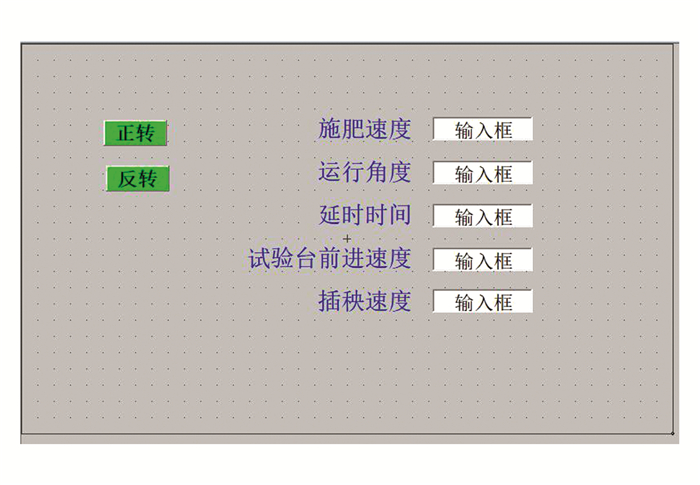
    在Micro Win Smart平台使用梯形图编程语言编写程序，程序所实现的功能主要包括试验台运行参数录入、装置工作参数实时采集、步进电机的延时启动等. 系统程序流程：系统初始化，装置运行参数录入，等待插秧运动信号，检测到运动信号后，将信号传至PLC，PLC控制步进电机实现间歇施肥，主程序片段如图 6所示. 在Mcgse组态环境软件中，进行人机交互界面设计并导入触摸屏，试验台开机后，点击调出操作界面如图 7所示，设置施肥、行进、插秧3种速度参数以及步距角与延时时间，进而精确控制施肥装置的行进、插秧以及施肥作业的启动与停止.

2.   穴式施肥装置性能仿真

  • 为探究穴式施肥装置的化肥颗粒的成穴性、插秧点与施肥点的位置耦合关系的合理性，运用EDEM软件对施肥装置的施肥性能进行仿真试验与分析.

    仿真准备阶段：利用UG软件按照1∶1的尺寸绘制试验装置三维仿真模型，存为SFSY. stl文件. 在EDEM软件设置肥料颗粒和施肥装置各组成部件材料的物理特征参数以及二者相互作用的力学特性参数，如表 2所示. 由肥料颗粒的三轴尺寸测定试验设置肥料颗粒的平均直径为3.5 mm; 因肥料颗粒的球形率为94%，为简化运算选用单粒球体颗粒模型对肥料颗粒进行仿真建模，并由软件求得颗粒质量为2.5×e-5 kg，颗粒体积为13.4×e-8 m3.再将试验装置的模型文件SFSY. stl导入已完成参数设置的SFSY. dem文件中，以实际工况下的水稻插秧机常规作业速度为参考，设置低、中、高3种作业速度进行穴式施肥仿真试验，并设置具体的仿真参数. 最后，选择肥料颗粒之间、肥料颗粒与装置之间的接触力学模型为Hertz-mindlin(no-slip)模型.

    排肥螺旋的转速由式(15)计算得到，式(16)计算得到螺旋的零水平单圈排肥量P.

    式中：Δt为每次穴施肥的排肥时间，s; n为每次穴施肥螺旋旋转的圈数，r; R为螺旋轴半径，mm; D为螺旋轴直径，mm; ψ为化肥填充系数，取0.9; S为螺旋螺距，m; d为螺旋内径，m; P为单圈排肥量，g/r; N为螺旋转速，r/min.

    仿真求解阶段：设置颗粒数量为1 500粒，瑞利时间步长为25%，仿真总时长为14 s，仿真试验过程的记录时间间隔为0.001 s，Cell Size设置为颗粒最小半径的2倍，网格大小为3.5mm，如图 8所示.

    仿真后处理阶段：隐藏试验无关项，并添加Mass Flow Sensor(质量流量监测工具)对穴施肥仿真试验数据进行采集，选取穴施肥仿真过程中的关键时刻，得到如图 9所示的仿真过程详细图. 仿真开始时，自Cylinder(颗粒工厂)全封闭中瞬间生成1 500粒颗粒; 0~0.5 s为压实阶段，速度为0.2 m/s的polygon(真实多边形片体)对颗粒堆进行加速压实以模拟自然条件下的肥料颗粒堆积; 0.5~3.5 s为充肥阶段，使颗粒充满搅龙与护肥管形成的储肥空间; 3.5~14 s为模拟穴施肥作业阶段，通过排肥螺旋的启停实现穴施肥.

    对Mass Flow Sensor采集到的试验数据，选取折线图处理方式，以时间t为x轴，以Mass Flow Rate(质量流量监测率)为y轴，由Origin软件绘制得到图 10. 其中穴距T、穴施肥量M的计算方法如下

    式中：r为化肥质量流量，kg/s; Δt为间歇施肥周期，s.

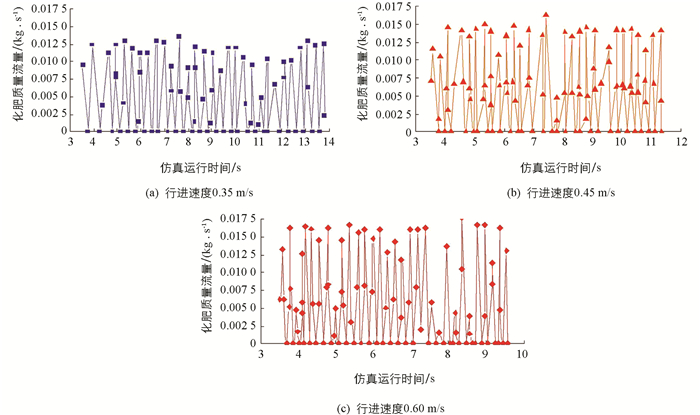
    试验表明：当行进速度为0.35 m/s的低速水平时，装置用时10.4 s施肥30穴，平均穴距12.51 cm; 行进速度为0.45 m/s的中速水平时，7.5 s施肥30穴，平均穴距12.21 cm; 行进速度为0.6 m/s的高速水平时，6.1 s施肥30穴，平均穴距11.96 cm.

    由图 10可知，当装置在行进速度为0.35 m/s的低速水平作业时，波峰接近于间歇施肥计算量，随着行进速度变大，虽然波峰波动较大，但波峰波谷分界显著，说明装置在0.35~0.6 m/s的作业速度范围内时，成穴性能以及施肥点与插秧点的耦合关系都较好，虽然随着行进速度的增加逐渐减弱，但仍满足水稻穴施肥农艺要求.

3.   装置的性能试验与分析

  • 依据NY/T1003-2006《施肥机械质量评价技术规范》开展试验数据测定. 试验时间：2022年4月; 试验地点：黑龙江八一农垦大学播种与收获试验室; 试验设备：穴式水稻侧深施肥试验台、水稻侧深施专用复合肥(云天化牌)、电子秤(型号JD200-3)、卷尺等.

    • 3.1.   试验方法

  • 穴式水稻侧深施肥试验台实物如图 11所示.

    在装置水平绝对速度为零时，更换不同排肥能力的螺旋搅龙，在护肥管下方放置集料器，通过集料器从护肥管出口收集肥料并称质量，称质量精度为0.1 g. 每次试验收集10次间歇排肥总量并求平均值，重复3次，根据式(19)至式(22)计算一致性变异系数获得螺旋搅龙的实际排肥能力. 以施肥装置的行进速度、螺旋的单圈排肥量、排肥口距地面高度为试验因素，选择苗-肥纵向距离合格率、排肥量稳定性为响应指标，通过单因素试验研究各因素对响应指标的影响，通过多因素试验研究各因素的交互作用对响应指标的影响. 依据试验方案所确定的作业参数，在试验装置的人机交互界面输入各参数进行调节.

    式中：S为标准差; V为变异系数; H为施肥总次数; Y为施肥位置合格率，%; n为施肥位置合格次数; xi为每次测定的化肥质量，g.

    应用Excel 2013及Design-Expert软件进行数据处理和分析. 以装置的行进速度、排肥高度、排肥能力为试验因素，选取排肥位置合格率与排肥稳定性为响应指标，开展三因素五水平二次回归正交组合试验，每次试验重复3次求得平均值作为试验结果. 试验因素水平编码如表 3所示，试验方案与结果如表 4所示.

    • 3.2.   试验结果与分析

  • 通过Design-Expert软件对试验结果进行回归分析，得到施肥位置合格率y1和排肥稳定性y2的二次回归方程分别为式(23)和式(24)，并检验各项对响应指标的显著性.

    如表 5所示，对施肥位置合格率影响极显著的为x1，x3; 影响显著的为x12，x32; 影响较显著的为x2，x1x3，x22; 影响不显著的为x1x2，x2x3. 失拟项p=0.161 8＞0.1，说明响应指标与试验因素存在显著二次关系，模型拟合程度好，剔除不显著项后的回归方程为

    如表 6所示，对排肥稳定性影响极显著的为x3; 影响显著的为x12，x32; 影响较显著的为x1，x1x3，x2x3，x12; 影响不显著的为x2，x1x2. 失拟项p=0.263 2＞0.1，说明响应指标与试验因素存在显著二次关系，模型拟合程度好，剔除不显著项后的回归方程为

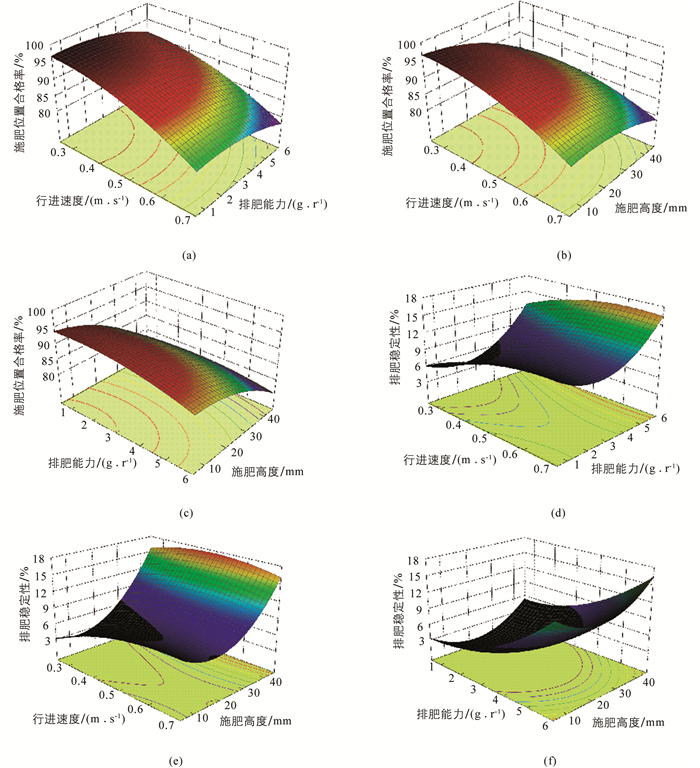
    为直观表现出试验因素与响应指标之间的关系，使用Origin软件得到施肥位置合格率和排肥稳定性响应曲面，如图 12所示.

    由图 12中(a)、(b)可知，当行进速度不变，排肥能力和施肥高度减小，施肥位置合格率均有缓慢增大趋势，施肥高度的影响较明显，这一现象的主要原因是肥料颗粒排肥阶段为抛物线运动，其运动时间与施肥高度有关; 由图 12中(a)、(c)可知，当排肥能力不变，行进速度和施肥高度减小，施肥位置合格率均增大，行进速度的影响较明显，主要原因是除了时间以外行进速度是唯一决定肥料颗粒被排出后所做抛物线运动时水平位移大小的影响因素; 由图 12中(b)、(c)可知，当排肥高度不变，行进速度和排肥能力均增大，施肥位置合格率都有减小的趋势，原因是二者都直接增加了化肥颗粒被排出后所做抛物线运动时的水平速度. 由图 12中(d)、(e)，图 12中(d)、(f)和图 12中(e)、(f)可知，当行进速度不变，排肥能力和施肥高度增大，排肥稳定性均有增大的趋势; 当排肥能力不变，行进速度和施肥高度增大，施肥位置合格率均有增大的趋势; 当排肥高度不变，改变行进速度对响应指标的影响不明显，增大排肥能力，施肥位置合格率增大，共同原因是3种试验因素的增加，减小了排肥时间，使肥料颗粒在被排出后位置分布更加集中. 由各项回归系数F结合回归各项对试验指标贡献率(δ)公式(27)、试验因素对响应指标的贡献率(Δj)公式(28)，经过计算得到试验因素对响应指标的贡献率，如表 7所示. 试验因素对施肥位置合格率的贡献率由大到小依次为行进速度、施肥高度、排肥能力.

    式中：δj为xj因素的一次项贡献率，δjj为xj因素的二次项贡献率，δij为xj因素的交互项贡献率.

    • 3.3.   试验结果的目标优化与验证

  • 为发挥装置的最佳工作性能，对试验因素进行优化设计，建立参数化非线性规划数学模型，以变异系数回归模型为目标函数，以试验因素和响应指标的取值范围为约束条件，利用Design-Expert软件求解目标函数的最优解.

    得到装置的最优解为行进速度0.47 m/s，排肥能力2.69 g/r，施肥高度16.7 mm，此时施肥位置合格率和排肥稳定性的综合效果最优，分别为93.02%和6.52%. 根据优化结果确定工作参数组合，以最优解的参数设计验证试验，试验结果分别为施肥位置合格率91.23%和排肥稳定性7.15%，与优化结果基本一致，穴式水稻侧深施肥装置的施肥性能满足穴施肥的农艺要求.

4.   结论

  • 1) 设计了穴式水稻苗-肥同施水稻侧深施肥装置，通过对垂直螺旋内肥料颗粒的排肥运动分析、秧爪运动轨迹及施肥点的确定分析，设计了控制系统的软、硬件，通过调整延时时间实现插秧点与施肥位置的耦合.

    2) 运用EDEM软件对施肥装置的穴施肥性能进行仿真试验，结果表明：在0.35~0.6 m/s的行进速度范围内，施肥装置的穴式施肥性能都较好，随着行进速度的增加，性能逐渐减弱，但均满足水稻穴施肥农艺要求.

    3) 设计了三因素五水平正交旋转组合试验，对试验结果进行了响应曲面分析，得到在不同响应指标下各试验因素的贡献率排序. 建立并求解参数化非线性规划数学模型，得到最优解为行进速度0.47 m/s，排肥能力2.69 g/r，施肥高度16.7 mm. 通过对最优解进行验证试验，得到施肥位置合格率和排肥稳定性分别为91.23%和7.15%，符合穴式水稻侧深施肥质量标准.

参考文献 (26)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回