-
开放科学(资源服务)标志码(OSID):

-
经济繁荣和技术进步推动科技不断创新,同时科技创新又反过来驱动经济快速发展[1-3]. 为了促进科技项目的有效管理,规范科技项目的投资与实施,建立科学、可信的科技项目评估制度十分必要[4-6]. 赵玲等[7]为了推进金融与科技的有机结合,将层次分析法(Analytic Hierarchy Process,AHP)与数据包络分析法(Data Envelopment Analysis,DEA)进行融合,提出了针对杭州科技金融绩效分析的AHP-DEA法. Kim等[8]通过制定一个建筑物及拆除废物管理绩效评估框架,综合保证了利益相关者的相关权益. 王宗军等[9]针对烟草行业商业系统相关的项目绩效分析问题,通过在3E原则基础上对湖北省烟草项目进行分析,并在AHP和熵权法的基础上构建了科技项目绩效评估体系. 本文在随机层次分析法(Stochastic Analytic Hierarchy Process,SAHP)与云模型等理论基础上,构建了SAHP-云模型评估方法,旨在提升科技投入项目绩效评估的合理性与科学性. 由于当前的项目绩效评估方法存在主观性与随机性较强的缺陷,因此本文提出的综合评价方法理论上解决了评估随机性的问题,具备一定的创新性,同时在实际应用上本文的综合评价方法相较于以往的研究简化了评估过程,并在遵循随机性的同时保证了结果的真实性.
全文HTML
-
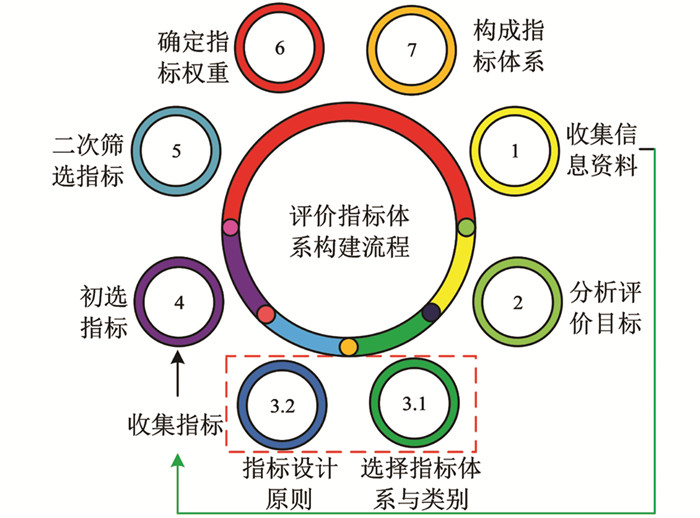
为了提升科技投入项目绩效评估的合理性,本文在SAHP与云模型等理论基础上,构建了科技投入项目绩效评估方法,并对其实际应用效果进行了分析. 科技投入项目绩效评估方法的构建,首先需要对其评价指标体系进行构建. 其具体步骤如图 1所示.
从图 1中可以看出:①构建流程首先是收集信息资料,此时同步收集相应的指标;②分析评价目标;③选择指标体系与类别,同时确定指标设计原则;④初选指标;⑤二次筛选指标,⑥确定指标权重;⑦构成指标体系. 在确定指标体系权重时,本研究为了减少指标的冗余度,降低专家评估的工作量,选择了信息敏感性理论来确定指标的客观权重,同时还充分考虑专家进行评价时的随机性,选择了SAHP来确定指标的主观权重. SAHP综合运用层次分析法与随机变量方法,同时综合考虑了人在做出决定时的不确定因素,其核心是把初始判别矩阵中的常量转换成随机变量,以此获得不同的随机矩阵[10-12].
利用SAHP计算主观权重首先需要建立层次结构模型;其次就是构建判断矩阵. 假定层次结构模型某个层次内存在多个指标,此时邀请专家根据1~9的标度法对多个指标进行指标间比较,得到的判断矩阵如式(1)所示.
式(1)中,D表示判断矩阵;dij为该矩阵中的元素,表示两个指标相比后的重要程度;n表示指标的个数;i和j表示序号不等的指标. 在确定矩阵中元素的具体值时,可以根据不确定情况来自由选择精确值、区间值或三角形模糊数的评分格式,从而较好地解决了专家评定行为的模糊性问题. 在得到判断矩阵后,可以将其转化为随机判断矩阵,此过程利用贝塔分布方法将评价值转换为随机变量;然后将随机变量转化为精确值;接着开始一致性检验;最后对单个专家评价的指标权重进行计算,这一步采用算术平均方法[13-15]. 值得注意的是,将判断矩阵转换为随机判断矩阵及将随机变量转换为精确值的两个步骤有别于传统层次分析法的步骤,专家能给出区间值和三角形模糊数的评分,从而减少了评估困难,避免损失有效信息,并用适当的随机变量表达了评估值,使评估结果不受精确值约束. 判断矩阵内所有的元素均以实数表示,之后的步骤与传统层次分析法相同.
利用算数平均方法对各专家的判断矩阵进行加权运算,求出该层次中各指标与高层指标之间的权重,其计算公式如式(2)所示.
式(2)中,ωk′表示随机判断矩阵下的权重,bij表示随机变量dij转换为的精确值,bkj表示专家k针对指标j评价的精确值,t表示指标i的最大值,k表示专家数,计算出专家评估下各项指标的最终权重,相关计算公式如式(3)所示.
式(3)中,ωk表示最终的主观权重,λk表示专家k的权重. 在确定主观权重后,可以利用信息敏感性理论确定客观权重[16-18],相应的计算公式如式(4)所示.
式(4)中,
$\overline{\omega_k}$ 表示客观权重,βk表示信息敏感性. 将客观权重与主观权重进行组合可以求出综合权重. 综合赋权法是综合主、客观赋权的成果而提出的一种综合赋权方式[19-21]. 本研究采用乘法合成归一法来确定综合权重,其计算公式如式(5)所示.式(5)中,σ表示综合权重,l表示评估指标的相关编号,m为最大编号,ωl和
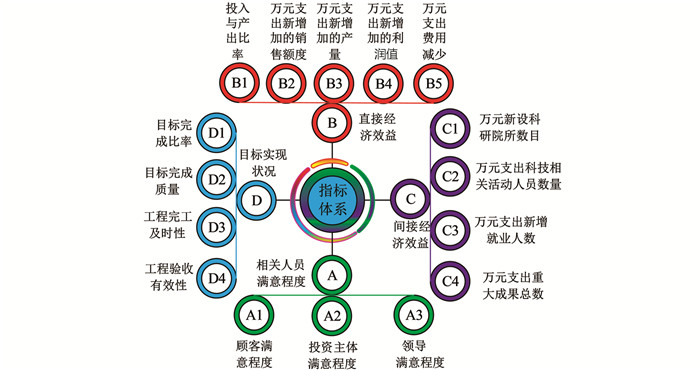
$\overline{\omega_l}$ 表示评估指标主客观权重. 在此基础上,本研究构建的指标评价体系中包含了4个1级指标及16个2级指标. 4个1级指标分别用A,B,C,D表示,2级指标分别用A1,A2,A3,B1,B2,B3,B4,B5,C1,C2,C3,C4,D1,D2,D3,D4表示. 其内容如图 2所示.从图 2中可以看出,4个1级指标分别为相关人员满意程度(A)、直接经济效益(B)、间接经济效益(C)及目标实现状况(D). A指标下分别为顾客、投资主体及领导满意程度;B指标下分别为投入与产出比率、万元支出新增加的销售额度、万元支出新增加的产量、万元支出新增加的利润值、万元支出费用减少;C指标下分别为万元新设科研院所数目、万元支出科技相关活动人员数量、万元支出新增就业人数、万元支出重大成果总数;D指标下分别为目标完成比率、目标完成质量、工程完工及时性、工程验收有效性.
-
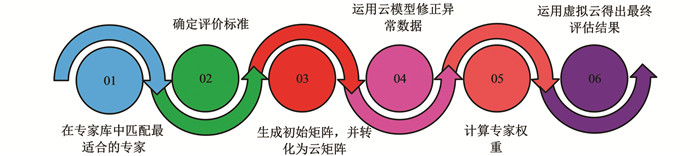
在SAHP确定主观权重、信息敏感性理论确定客观权重的基础上构建完成指标体系后,需要选用相关评价方法对其进行评价. 本研究综合考虑后选择云模型与专家评价法对其进行评价,根据构建完成的指标体系制定的绩效评估实施流程如图 3所示.
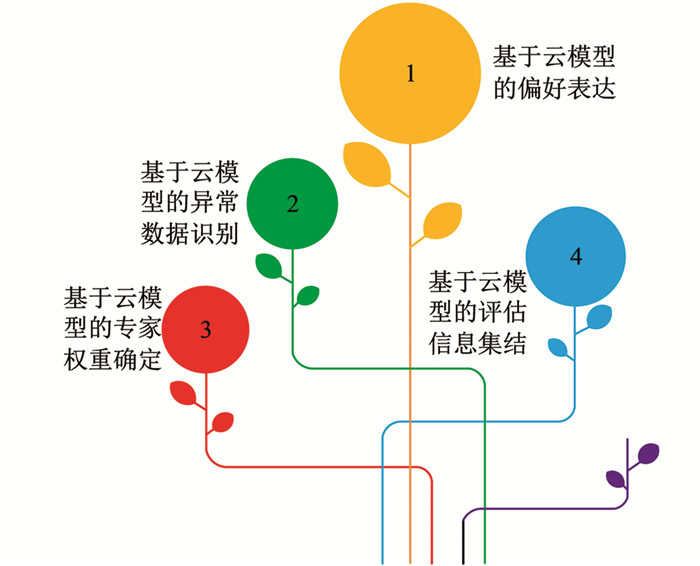
从图 3中可以看出,绩效评估实施流程总共分为6步;①针对特定的被评估项目,利用内容和专家精确性的推荐方法从专家数据库中选出最适合的专家;②按照指标体系设计出科学工程业绩评估表;③根据专家评估结果,建立一个初始评估矩阵,并根据该模型的偏好表达式,把评估矩阵转换为“云”矩阵;④利用云模型对评估中出现的异常进行识别校正,得出“云”矩阵;⑤根据专家的初步评估矩阵来确定各专家的权重;⑥利用云模型中的虚拟云产生算法,从下到上收集评估信息,并用“浮动云”来表示各标准层面的评估资料,将“浮动云”集中在各个标准层,形成一个代表项目最终评估结果的“综合云”. 在绩效评估流程中,本研究在云模型的基础上优化了传统的模糊综合评价方法,将模糊与随机相结合,避免专家评价的主观、随意性,从而提高了评价的精确性. 其具体内容如图 4所示.
从图 4中可知,具体内容包含偏好表达、识别异常数据、确定专家权重、评估信息汇总. 云模型偏好表达中比较重要的就是熵值(En)、超熵值(He)、期望值(Ex). 原始He和En代表了评估结果的随机与模糊性. 另外,传统的专家评价法受主观行为影响比较大,从而会造成评估结果可靠性大幅度降低. 为了避免个别异常数据对整个评估结果造成不必要的影响,需要对这些异常数据进行识别. 其评估结果矩阵如式(6)所示.
式(6)中,S表示评估结果矩阵,m′表示专家的个数,n表示评估指标的个数;s表示矩阵内部元素. 由于评估指标已经转化为云形式,因此将评估指标结果异常数据设置为Sij=(Ex1,En1,He1). 依据云模型的修正原则,异常数据的修正表达式如式(7)所示.
式(7)中,Ex1′代表期望的最可能取值,其修正结果为Ex的均值. En′和He1′分别表示修正后的熵值和超熵值,其修正后均表示评价云的最小值. 在确定专家权重时,首先需要确定专家的不确定度与偏差度,其表达式如式(8)所示.
式(8)中,ψ(Sk)表示专家的不确定度,t表示另一个专家,其和专家k不是同一个专家,γ(Sk)表示专家的偏差度,D表示模糊评价中两个模糊语言数值的相离程度,sij和sjt表示专家k和t对指标j的评价结果. 依据不确定度和偏差度可以确定专家的两个客观权重,并得出最终的综合权重,其表达式如式(9)所示.
式(9)中,λk1表示专家的第1个客观权重,λk2表示专家的第2个客观权重,λk表示综合权重,α和β表示权重系数,二者之和为1. 并处于(0,1)之间;Sk表示专家k的评价结果矩阵. 最后,在云模型基础上集结评价信息是为了得出最终评估结果. 例如,某位专家已经将A1,A2,A3这3个指标的模糊评估信息转换成了3朵云,但是并没有直接对三者的一级指标进行评估,所以A指标的评估结果是3个2级指标评估结果的集合,因此可以将A指标称之为虚拟云. 虚拟云根据特定用途对每个基云的数据特性进行运算,并将其转化为新的数据特征,在虚拟云架构中可以划分为浮动云和综合云[22-24]. 本研究利用浮动云生成方法,对指标层次的指标进行评估,得出了该指标的评价结果;并采用集成云产生的方法,对各标准层次指标进行汇总,得出了科技投入项目的总体得分[25].
科技投入项目绩效评估关乎知识产权密集型产业升级. 在知识产权密集产品中其接近度与产业升级的可能性之间存在正相关. 同时,其动态演技以临近性升级为主,跳跃性升级为辅. 以中国为例,知识产权密集产品的临近效应可以起到推动作用. 另外,知识产权密集型产品的邻近能力累积,能够降低其所需能力水平,增加对产业升级的负向影响.
1.1. 基于SAHP-信息敏感性的科技投入项目绩效评估指标体系建构
1.2. 基于云模型的科技投入项目绩效评估流程分析
-
为了验证SAHP-云模型的有效性,本研究在相关科技项目网站上随机邀请10位相关专家作为评审小组成员,对相应指标之间的重要性做出判断. 此过程首先依据专家知识体系和工作经验进行必要的筛选,并在筛选完成后的专家群体中利用随机法来邀请,这样既保证了专家可信度下限,也可以充分发挥SAHP的随机性优势. 本研究选择的科技投入项目信息为“科学基金共享服务网”中的内容,在研究开始前需要对权重进行确定,其结果如图 5所示.
在图 5中,依据信息敏感性理论,本研究删除了B3,C1及D1这3个指标,以此减少信息冗余度. 图 5中3张图表示项目绩效评估体系的主、客观权重和综合权重结果. 从图 5a中可以看出,评估体系主观权重B指标值最大,为0.435. 从图 5b中可以看出,客观权重13个指标呈递减趋势,A指标下的客观权重最大,表明在绩效评估中相关人员的满意程度占较大比例. 从图 5c可以看出,B指标下B4权重值最大,为0.15,表明在绩效评估中新增利润占较大比例. 在此基础上,本研究依据百分制原则,利用云模型将评价等级划分为5个标准:S-2(0-40),S-1(40-60),S0(60-75),S1(75-90),S2(90-100).
依据云模型优化的模糊综合评价内容,本研究首先对云模型偏好表达进行了实验验证. 由于篇幅受限,只用A指标下专家原始评估数据云模型表示. 另外,本研究还运用云图对A1指标进行评估,其结果如图 6所示.
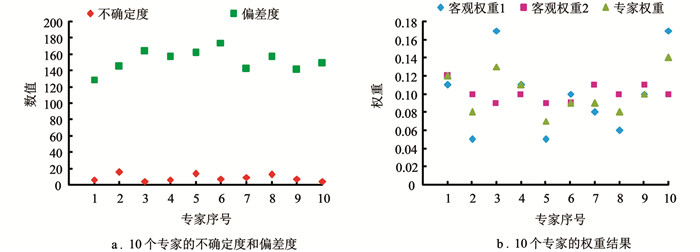
从图 6中可以看出,专家评估结果的期望评分大致维持在63~94分之间. 另外,从两个专家对A1指标的评估结果来看,专家5的横轴以10为单位,明显比专家7的宽泛度更高,表明专家5的评估结果不确定性更高. 综合来看,云模型可以比较科学地表示专家的评估结果. 同时,云模型的En值和He值也充分体现了专家评价的随机性. 在此基础上,本研究利用云模型来确定专家权重,依据专家的不确定度与偏差度来计算,其结果如图 7所示.
从图 7中可以看出,专家2的不确定度和专家6的偏离度最大,分别为15和174,表明两位专家存在个人经验、对项目缺乏了解及意见不符等问题. 将专家不确定度和偏差度赋值为0.5后,得到的专家权重维持在0.08~0.14之间. 其中,专家10的权重最大,为0.14. 在专家权重给出后,本研究有效集结了专家和1,2级指标的信息,计算出浮动云,其结果如表 1所示.
从表 1中可以看出,B4指标即万元支出新增加的利润期望值最大,为89.75;D3指标的熵值最小,为0.71,说明10位专家在该指标上的看法较为一致,而A2指标和A3指标的熵值为2.82和2.81,数值最大,表明10位专家在两个指标上分歧最大,因此其模糊性与随机性最大. 在1级指标中,D指标的熵值最小,看法最为一致;A指标的熵值最大,随机性最大,得分稳定性较低. 综合来看,该科技投入项目的期望值为81.12分,超熵值为0.12,处于较低水平,表明专家组对该项目的评估结果较为一致,同时也表明SAHP-云模型方法在该科技投入项目绩效评估中降低了评分的模糊性和随机性,提升了评估结果的科学性与合理性.
-
针对当前项目绩效评估主观性强、合理性较低的问题,本研究引入SAHP和云模型理论,构建了SAHP-云模型评价方法,并将其应用于实际的科技投入项目,在云模型表示、专家权重确定及双指标层3个方面实验的基础上,验证其有效性. 实验结果表明,从云模型表示结果来看,单论A1指标专家5比专家7宽泛度更高,符合原始数据云模型表示结果. 从专家权重确定结果来看,专家权重维持在0.08~0.14之间,其中专家10的权重最大,为0.14. 从专家与2级指标信息集合结果来看,1级指标中D指标熵值最小,为0.92,A指标熵值最大,为2.76,而综合云结果超熵值为0.12,处于较低水平. 综合来看,本研究给出的SAHP-云模型方法在科技投入项目绩效评估上基本符合原始专家评估结果,同时也降低了专家评估中的模糊性和随机性,从而具备较强的科学性和合理性. 值得注意的是,本研究采用的虚拟云在指标信息集结上还需要更深一步探讨,从而构建出更完善的数据处理方法.



 下载:
下载: