-
开放科学(资源服务)标识码(OSID):

-
Zadeh通过发表的“Fuzzy sets and information granularity”[1],对信息粒进行了定义,开启了信息粒度化思想的探索. 随后,Lin[2]提出了粒计算(granular computing)的概念. Yao等[3]则不断深入研究粒计算与粗糙集领域,并将其应用在知识挖掘、机器学习等领域. 21世纪初,众多研究学者纷纷加入粒计算这一新兴研究领域,并不断取得突破与创新. 苗夺谦等[4]通过对粒计算理论与方法的研究,展示了粒计算在人工智能领域的前景与应用. Ruan等[5]提出的信息粒化方法有助于减少时间序列分析的时间成本. 此外,朱鹏飞等[6-8]在邻域约简和分类等领域也有显著突破. 粒计算中的粒化概念是人类认识世界的重要组成部分,在特征选择、处理复杂数据等方面发挥着重要作用.
在人类活动和自然研究中,普遍存在聚类问题. 当前提出的聚类方法旨在对大量未知标注的数据进行分类,通过数据中个体与类簇相关的属性,将个体分类到各个类簇中. 在这个过程中,同一类簇中的个体属性更为相似. 人们常用的聚类算法[9]包括划分聚类、密度聚类、基于混合分布的聚类等. 其中,最为人熟知的是k-means算法[10-11],它是一种划分聚类方法. 由于k-means算法易于实现且运行时间较短,因此成为一种广泛使用的聚类分析算法,并且在各个领域都取得了不错的效果. 然而,该算法也存在一些缺点,尤其是对于稀疏或局部分布不均匀的数据,其效果往往并不理想. 另一种常见的聚类方法是密度聚类[12],其原理是只要区域内的点密度高于某一阈值,就将其归入相近的类簇中. 代表性的算法有DBSCAN[13]以及针对其进行优化的OPTICS[14]. 为了解决密度分布不均匀导致聚类效果不佳的问题,孙璐等[15]提出了GFDBSCAN,Rodriguez等[16]提出了基于密度峰值的聚类方法. 与划分聚类相比,密度聚类依赖于密度而不是距离的特点,因此能够对任意形状的簇进行聚类,但是其空间复杂度相较其他算法要高许多,计算开销更大. 基于混合分布的聚类方法是通过假设簇内符合多元正态分布,判断数据样本符合各个样本分布的概率,不断迭代更新,直至得到数据集的聚类情况. 这种方法主要被人们运用于图像聚类目标识别等领域,并不断加以改进. 此外,聚类还有基于网格聚类[18]、层次聚类[19]、谱聚类等算法.
谱聚类[20]是一种源自图论的聚类方法,它具有处理任意形状的数据集的能力,并且在稀疏数据聚类方面表现十分出色. 因此,谱聚类在数据挖掘、图像分割、模式识别以及遥感等领域中得到广泛应用. 近年来,由于谱聚类独特的优势,引起了学术界的广泛关注. 孔万增等[21]提出了利用矩阵的特征向量和本征间隙来自动确定类别个数的优化方法. Chen等[22]对划分准则进行了改进,将算法的时间复杂度降至O(n2c). 在谱聚类优化中,相似矩阵的构造方法是一个关键的焦点,因为谱聚类对相似矩阵极为敏感. 如果构造出的相似矩阵不能很好地反映数据之间的近似关系,其效果就难以保证. 因此,一个良好的相似矩阵的构造对于谱聚类算法至关重要. 邻域粒[23]能够有效地反映数据之间的近似关系,本文针对相似矩阵的构造,结合邻域粒及其距离度量方式,提出了一种新的相似矩阵构造方法,从而得到了基于邻域粒的谱聚类算法. 该方法首先通过在单一特征上对样本进行邻域粒化的方式形成邻域粒子,然后将属于同一样本的粒子组合构造成粒子向量. 通过定义邻域粒向量的距离度量,用粒向量的距离代替常规径向基核函数中的欧式距离,从而得到经过邻域粒化后的数据相似矩阵. 由于样本粒化是通过全局信息进行的,使得样本具有了全局性,从而能够更好地反映数据之间的近似关系. 最后,通过与传统聚类算法在UCI数据集上的比较,实验结果表明邻域粒化的方式在谱聚类中取得了不错的效果.
全文HTML
-
传统的聚类方法输入的数据是样本数据,本文通过粒子与粒向量的构造方法,将数据在单一特征上进行邻域粒化,获得了粒子并推广到多个特征上,通过数据的多个粒子进行组合,构造出粒向量. 并且在粒子与粒向量上,同样能进行数学运算.
设聚类系统为
$C=(R, P)$ ,其中数据集合为$R=\left\{r_{1}, r_{2}, \cdots, r_{n}\right\}$ ,特征集合为$P=\left\{p_{1}, p_{2}, \cdots, p_{m}\right\}$ . 对于确定数据r∈R,其单一特征$p \in P, v(r, p) \in[0, 1]$ 表示进行归一化后,数据r在单一特征p上的值.对于聚类系统
$C=(R, P)$ ,对于不同的数据r1,r2∈R,其单一特征p∈P,则数据r1和r2在单一特征p的曼哈顿距离为其中:v(r1,p)表示数据r1在单一特征p上的值.
定义1 给定聚类系统
$C=(R, P)$ ,对于不同的数据r1,r2∈R,其单一特征p∈P,并设定邻域参数为δ,则定义数据与数据是否为邻域的判别函数为其中:φ(r1,r2)=1表示数据与数据之间在该邻域范围内互为邻域;φ(r1,r2)=0则表示数据与数据在该邻域范围内不相邻.
定义2 给定聚类系统
$C=(R, P)$ ,对于不同的数据r1,r2∈R,其单一特征p∈P,则数据r在特征p上的邻域粒子定义为上述lj=φ(r1,r2),代表二者是否相邻.
定义3 给定聚类系统
$C=(R, P)$ ,对于确定数据r∈R,其有特征子集A⊆P,设A={p1,p2,…,pm},则r在特征子集A上的邻域粒向量定义为上述gm(r)代表数据r在特征pm上构造的邻域粒子.
由此可知,邻域粒子由0和1组成,表示数据在设定的邻域参数范围内的相邻关系. 由于邻域粒向量是由邻域粒子构成的,因此与传统向量的实数元素不同,其元素是由集合组合而成的.
定义4 给定聚类系统
$C=(R, P)$ ,对于确定数据r∈R,其单一特征p∈P,则数据r在特征p上的邻域粒子gp(r)的大小定义为由邻域粒子的定义可知,其范围为:1≤g1(r)≤n.
定义5 给定聚类系统
$C=(R, P)$ ,对于确定数据r∈R,其有特征子集A⊆P,设A={p1,p2,…,pm},则数据r在特征子集A上的邻域粒向量的大小定义为由邻域粒向量的定义可知,其大小范围为:
$\sqrt{m} \leqslant\left|\boldsymbol{G}_{\boldsymbol{A}}(\boldsymbol{r})\right| \leqslant n * \sqrt{m}$ .
-
定义6 给定聚类系统
$C=(R, P)$ ,特征集合为P={p1,p2,…,pm}. 对于不同数据r1,r2∈R,其邻域粒向量在特征集合P上,分别表示为则其加、减、交、并与异或运算定义为
定义7 给定聚类系统
$C=(R, P)$ ,特征集合为P={p1,p2,…,pm}. 对于不同数据r1,r2∈R,其邻域粒向量在特征集合P上,分别表示为则2个邻域粒向量的相对距离定义为
其中:
$|P|=m$ ,由上述定义可知,其相对距离满足:0≤d(GP(r1),GP(r2))≤1.定义8 给定聚类系统
$C=(R, P)$ ,特征集合为P={p1,p2,…,pm}. 对于不同数据r1,r2∈R,其邻域粒向量在特征集合P上,分别表示为则2个邻域粒向量的绝对距离定义为
其中:
$|P|=m, |R|=n$ . 由上述定义可知,其绝对距离满足:定理1 邻域粒向量的相对距离作为距离度量,要满足以下3个性质:
性质1 非负性,0≤d(GP(r1),GP(r2))≤1;
性质2 对称性,d(GP(r1),GP(r2))=d(GP(r2),GP(r1));
性质3 三角不等式,d(GP(r1),GP(r2))+d(GP(r2),GP(r3))≥d(GP(r1),GP(r3)).
关于以上性质证明如下:
1) 由gi(r1)⊕gi(r2)=gi(r1)∨gi(r2)-gi(r1)∧gi(r2)可知
则
由P={p1,p2,…,pm}可知|P|=m,因此
则
所以,0≤d(GP(r1),GP(r2))≤1成立.
2) 因为gi(r1)∨gi(r2)=gi(r2)∨gi(r1),gi(r1)∧gi(r2)=gi(r2)∧gi(r1),可知
因此,d(GP(r1),GP(r2))=d(GP(r2),GP(r1))成立.
3) 因
所以
成立,所以d(GP(r1),GP(r2))+d(GP(r2),GP(r3))≥d(GP(r1),GP(r3))成立.
同理可证,邻域粒的绝对距离也满足非负、对称、三角不等式以上3个性质.
-
基于邻域粒的谱聚类算法是一种方法,它首先将样本进行邻域粒化,然后通过计算邻域粒向量之间的距离来构造相似矩阵,最后进行正常的谱聚类. 不同于局部处理,邻域粒化是从全局出发对样本进行处理的. 邻域粒向量由邻域粒子构成,因此邻域粒化后的粒子与粒向量具有全局信息. 由于谱聚类对相似矩阵极为敏感,利用该方法构建的相似矩阵能更好地反映数据之间的近似关系,从而使得谱聚类达到更好的效果.
-
基于邻域粒的谱聚类算法的流程如下:首先对样本进行邻域粒化,将每个样本的单一特征邻域粒化为粒子,然后将这些粒子组合起来构成粒向量. 由于邻域粒化是通过全局信息进行的,因此同一簇内的粒向量之间的距离更为紧密,而不同簇之间的粒向量之间的距离相对更大. 基于这样的构造方式,得到的相似矩阵能够更好地反映数据之间的关系. 构建的邻接矩阵方法如下所示:
先将样本数据进行邻域粒化,粒化结果为GT=(GP(r1),GP(r2),…,GP(rm)). 此时,样本被邻域粒化后,可以采用粒向量的距离公式进行距离计算,并以此构建邻接矩阵W. 若采用粒向量的绝对距离,表示为h(GP(r1),GP(r2)),此时邻接矩阵W定义如下:
若采用粒向量的相对距离,表示为d(GP(r1),GP(r2)),此时邻接矩阵W定义如下:
谱聚类的主要思想是将所有的数据放置到图中,并用点表示,点之间的关系用边来表示. 其边的权值由点之间的相似性决定,如果相似性高,则权值高;如果相似性低,则权值低. 然后通过对图进行切割,确保子图内部的权值高,而子图与子图之间的权值低. 邻域粒化后的粒子具有全局性,能很好地满足这一思想,从而让谱聚类的性能更好,更有效地完成聚类任务.
-
具体的算法如算法1所示.
算法1 邻域粒谱聚类算法.
输入:聚类系统
$C=(R, P)$ ,其中数据集合为R={r1,r2,…,rn},特征集合为P={p1,p2,…,pm},降维后的维度K1,聚类维数K,邻域参数δ.输出:簇划分F=(f1,f2,…,fk).
① 样本集U邻域粒化为GT=(GP(r1),GP(r2),…,GP(rm));
② 计算邻域粒向量GP(ri)之间的距离后通过邻域粒距离使用径向基函数构建相似矩阵W;
③ 通过相似矩阵W构建度矩阵D;
④ 计算出拉普拉斯矩阵L以及标准化拉普拉斯矩阵
$\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{L} \boldsymbol{D}^{-\frac{1}{2}}$ ;⑤ 计算标准化的拉普拉斯矩阵最小的K1个特征值所各自对应的特征向量v;
⑥ 将各自对应的特征向量v组成的矩阵按行标准化,最终组成n×K1维的特征矩阵V;
⑦ 将特征矩阵V的每一行视为一个K1维的样本,共n个样本,用聚类方法将其分为K类;
⑧ 输出簇划分F=(f1,f2,…,fk).
谱聚类算法的运作需要一个聚类维数K,这通常需要借助于真实的标签信息来选取一个恰当的K值,或者使用肘部法等方法获得一个适合的K值. 此外,在邻域粒化过程中要对邻域参数δ进行设定,其与数据间的距离相关联,需要通过检验来确定一个合适的值.
3.1. 基于邻域粒的谱聚类原理
3.2. 邻域粒谱聚类算法
-
实验通过多个UCI数据集验证了提出的相似矩阵构造算法的有效性. 表 1描述了各个UCI数据集具体的相关信息. 在实验过程中,对数据进行了归一化处理,以消除算法运行过程中奇异样本带来的不良影响. 归一化后,所有数据会介于[0, 1]之间. 归一化公式如下:
在数据归一化后,将样本进行邻域粒化,形成粒向量. 在衡量粒向量之间距离时,有相对距离和绝对距离2种选择. 本次实验将分别验证相对距离和绝对距离的粒谱聚类算法的效果差别,并与使用谱聚类和其他传统聚类算法进行比较,以验证算法的聚类效果. 实验过程中,使用常用的聚类指标:聚类纯度(Cluster Purity,CP)和调整兰德指数(Adjusted Rand Index,ARI)作为评估指标,能够很好地展现对比实验的结果.
-
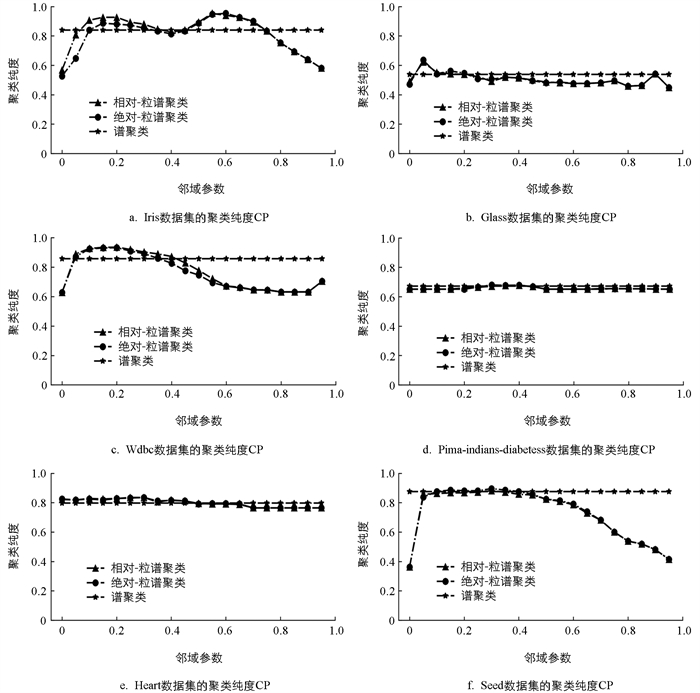
选用不同的邻域参数和距离度量方式对于样本之间的距离具有重要影响,可能导致构造出的相似矩阵结果大相径庭,从而直接影响聚类的效果. 为了深入了解在基于邻域粒的谱聚类算法中邻域参数和邻域粒距离度量对聚类效果的影响,我们进行了一系列实验. 选取的数据集具有真实标签,因此选用聚类纯度(CP)作为聚类性能评估指标. 鉴于之前对数据进行过归一化处理,将邻域参数设置为从0开始,以0.05为间隔,总共20组邻域参数,并分别采用邻域粒的相对距离和绝对距离进行实验. 不同数据集在这20组邻域参数和2种度量距离方式下的实验结果如图 1所示:
根据图 1(a),(c),(f)的实验结果,在Iris、Wdbc和Seed数据集上观察到以下情况:在Iris数据集中,当邻域参数为0.55时,2种不同距离的谱聚类算法均达到了相同的最高值0.953 3. 在Wdbc数据集上,当邻域参数为0.2时,基于邻域粒相对距离的谱聚类算法的CP值为0.935,而基于邻域粒绝对距离的谱聚类算法的CP值达到了0.933 2. 在Seed数据集上,当邻域参数为0.3时,基于邻域粒相对距离的谱聚类算法的CP值为0.881,而基于邻域粒绝对距离的谱聚类算法的CP值达到了0.895 2. 从结果可以看出,基于邻域粒相对距离构造的相似矩阵和基于绝对距离构造的相似矩阵在谱聚类算法中表现出的CP值最佳效果基本相同. 另外,CP值曲线均呈现“凸”型,表明过高或过低的邻域参数会导致构造出的相似矩阵不能很好地反映数据的情况,进而影响聚类算法的性能并导致聚类性能降低.
根据图 1(b),(d),(e)的实验结果,在Glass、Pima-indians-diabetes和Heart数据集上观察到以下情况:在Glass数据集上,当邻域参数为0.05时,基于邻域粒绝对距离和相对距离的谱聚类算法的CP值分别达到了0.616 8和0.640 2,随后在传统谱聚类算法的CP值0.542 1附近波动. 在Pima-indians-diabetes数据集上,当邻域参数为0.4时,2种算法的CP分别达到最大值0.677 1和0.678 4. 在Heart数据集上,当邻域参数为0.3时,2种算法的CP值同时达到相同最大值0.835. 在这3个数据集中,粒谱聚类算法的聚类纯度CP对邻域参数不是很敏感,大致在传统谱聚类算法的CP值附近波动.
综上所述,从邻域参数的角度来看,过大或过小的邻域参数都可能对聚类性能产生不良影响. 而从邻域粒距离度量的角度来看,距离度量对算法性能的影响不是很显著. 总体而言,存在适当的参数取值,可以使聚类效果达到最佳,甚至超过传统的谱聚类算法. 因此,与传统的谱聚类算法相比,利用邻域粒构建的相似矩阵能够在大多数数据集上取得更好的聚类性能效果.
-
本次实验将基于邻域粒相对距离和绝对距离的谱聚类算法与谱聚类算法、基于K近邻构造相似矩阵的谱聚类算法、GMM算法、Agglomerative Clustering算法和K-means算法进行对比. 采用上述UCI数据集,通过CP和ARI这2个聚类性能指标进行评价,其中2个指标的最大值为1,性能指标越高越好. 具体对比结果如表 2和表 3所示.
由表 2可知,在通过CP进行性能评估时,在Heart和pima-indians-diabetes数据集中,基于邻域粒距离的2种谱聚类算法的性能表现优于其他算法. 在Glass和Seed数据集中,基于邻域粒绝对距离的谱聚类算法性能最优. 在Iris和Wdbc数据集中,2种粒谱聚类算法得分虽然都高于原始谱聚类算法,显示出良好的聚类效果,但性能得分略低于GMM算法和基于K近邻的谱聚类算法.
由表 3可知,在通过ARI进行性能评估时,在Iris、Heart、pima-indians-diabetes和Seed 4个数据集中,2种距离的粒谱聚类算法的性能表现优秀,性能得分高于其他算法. 在Glass数据集中,基于邻域粒绝对距离的谱聚类算法性能是最优的. 在Wdbc和Glass数据集中,基于K近邻的谱聚类算法的性能要优于其他算法.
从以上实验结果可以看出,在所列举的数据集中,基于邻域粒距离的谱聚类算法的聚类性能均优于传统的谱聚类算法,并且优于大多数其他算法. 尽管在某些数据集上,该算法的性能指标略逊于GMM和基于K近邻的谱聚类算法,但通过邻域粒距离优化相似矩阵的构造,其性能指标得分与最优算法的性能指标得分基本相当. 与传统的算法不同,粒谱聚类算法利用邻域粒化技术在结构上取得了突破,使得数据在算法进行之前就得到处理. 这样处理后,簇内的粒向量距离更为紧密,而簇间的粒向量距离相较簇内的粒向量则更大. 因此构建的相似矩阵更能反映数据之间的关系,从而提升了谱聚类的聚类性能. 这使得谱聚类能够在不同形状的数据集上都展现出良好的性能.
4.1. 邻域参数和距离度量方式的影响
4.2. 聚类算法比较
-
本文结合谱聚类的相似矩阵构建过程,将粒计算思想与谱聚类相融合,提出了基于邻域粒的谱聚类算法. 该算法将邻域粒化技术引入到谱聚类算法的相似矩阵构造中. 通过全局信息进行邻域粒化,使得生成的粒向量具有全局性. 因此,簇内的粒向量距离更为紧密,而簇间的粒向量距离相对较大. 由此构建的相似矩阵更能够准确地反映数据之间的关系,从而提高了谱聚类的聚类性能. 最后,本文在常见的UCI数据集上进行了实验验证,结果表明基于邻域粒的谱聚类算法相比传统方法在聚类效果上表现更佳. 这一实验结果在不同形状的数据集上得到了验证,证明了基于邻域粒的谱聚类算法的可行性和有效性.



 下载:
下载: