由于测量的碎片粒子有可能从不同的入射角度进入探测单元，所以有必要对不同入射角度的粒子的探测效率进行研究，这对于提高测量数据的准确性是非常重要的. GEANT4^[17]是由欧洲核子研究组织(CERN)基于C++面向对象技术开发的蒙特卡罗应用软件包，可用于模拟粒子在物质中传播、与物质相互作用、探测器性能等各种高能物理实验^[18]. 本文采用该软件进行了光子收集效率的模拟.

最终的碎片能量探测一般采用闪烁体探测器. 闪烁体探测器具有测量能量范围大、性价比高、易制成不同的形状等优点. 一般每个探测单元由闪烁体和光电倍增管构成，闪烁体吸收射线后被激发，退激发后放出光子，产生的光子由光电倍增管收集，产生电信号被放大，最终被数据获取系统收集. 闪烁体产生的光子数与入射粒子的种类和能量都有关系，所以相同能量的粒子以不同的入射角度进入探测单元是否有相同的光输出信号，对于正确测定粒子的能量非常重要.

首先对实验组的CsI(Tl)闪烁体探测单元进行仿真模拟，分析粒子的不同入射角度进入探测器对于光子收集效率的影响. 模拟过程中，当入射粒子进入闪烁体后，产生荧光光子，根据光子是否落到闪烁体与光电倍增管接触的后表面来确定收集的数量从而计算效率. 分别以不同能量、不同入射角度、不同点源位置为单一变量，探讨对光子收集效率的影响. 通过对到达探测器后表面的光子进行计算和数据分析，得到仿真过程中不同变量数值对光子收集效率的影响，如表 1所示.

从上述模拟结果可知，粒子以不同入射角度、能量进入闪烁体探测器对光子收集效率的影响较小，保证了测量到的信号大小与入射粒子的能量成正比，因此用该探测器进行测量得到的结果是可信的.

原子核的结团结构一般处于激发态. 为了更好地了解如何计算入射粒子、靶核的碰撞过程及碰撞后产物的分布，有必要对原子核的激发过程进行仔细地计算. 本文运用质心系(Centre of Mass System，CMS，简称C系)来实现入射粒子与靶核碰撞和碎裂过程. 主要计算在C系中入射粒子与靶核发生碰撞、处于激发态的粒子进而发生碎裂2个过程，而最终的碎片用探测器可以测量出，这些输出的结果需要用实验室系(Laboratory System，LS，简称L系)坐标来描述，以便与实验的测量结果进行对比.

碰撞过程的计算在C系中有很大的优势，因为C系中参与反应的粒子总的线性动量始终为零. 在C系的反应过程中，粒子在碰撞前相向运动，而在碰撞后朝着相反的方向运动，故计算时会先将L系向C系转变，计算完成后，再将数据由C系的值转换为L系中的值并进行提取.

以核反应a+A→b+B为例. 其中a是入射粒子，A是靶子，B是剩余核，b是出射粒子，即本文选择的具有结团结构的原子核，一般用于研究原子核的激发态. 二粒子的质心定义为：

式中：$ \vec{r}_C, \vec{r}_a, \vec{r}_A$分别为质心C、a和A的坐标位置；m_a，M_A分别为a和A的质量，于是求得质心速度$ \vec{v}_C$为：

式中：$ \vec{v}_0$是a在L系下的速度. 在C系下粒子a的速度$ \vec{v} $为：

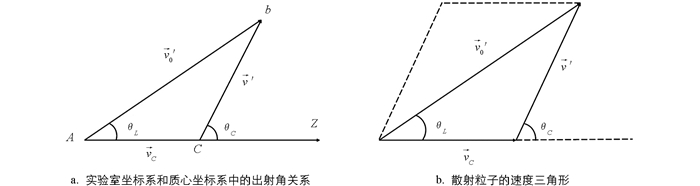
于是求得靶核质心速度$ \vec{u}$为：

图 1分别为L系和C系中出射角的关系，以及出射粒子在L系和C系中的速度三角形，其中$ \vec{v}_0$与$ \vec{v}'$分别为粒子出射后在L系和C系下的速度.

在L系中，反应前的总动能E_L为：

在C系中，反应前的总动能E_C为：

由式(3)和式(5)有：

式中：μ为约化质量，$ \mu=\frac{m_a M_A}{m_a+M_A}$，故可求得反应前的总动能E_C为：

可得质心速度值v_C为：

C系中粒子出射的动能ε_C为：

式中：m_b为b的质量. 同理可得C系中反冲核(B)的动能ε_C^r为：

式中：M_B为B的质量. 在C系中，根据能量守恒有：

式中：E_C为C系反应前的总动能；Q为反应能. 将式(11)代入式(12)后可得C系中粒子出射的动能ε_C为：

由式(13)可以看出在C系中，出射粒子的能量ε_C与出射角θ_C无关.

由于核反应的反应道非常多，碎裂反应或转移反应发生的概率都比较低，在做实验时，提高探测器的收集效率很有必要，因此可以根据该过程计算出碎裂后碎片的角分布，从而推算出探测器的最佳摆放位置，提高探测效率，为实验的探测器如何摆放提供指导.

碎裂反应一般通过加速器束流线选择要研究的原子核，通过打靶后该原子核被激发到核内有结团结构的激发态，然后碎裂发射不同的碎片. 可以根据测得的碎片方向、能量及种类，回推出结团结构，并结合理论计算分析相应的结构. 根据上一节对碰撞过程的描述，靶核A和剩余核B相同，入射粒子a和出射粒子b相同，是本文要研究的原子核，只是原子核b此时处于被激发到有结团结构的激发态. 具有结团结构的原子核b然后碎裂成2个碎片，通过测量碎片的位置和能量，就可以得到原子核b所处的激发态.

碎裂反应的测量一般采用闪烁体探测器阵列，每个探测单元都可以给出所测量粒子的能量和位置，根据这些信息就可以回推出原子核的激发能，但是需要考虑探测器和靶子之间的距离问题：如果太远，则相对于靶子张开的立体角太小，造成碎裂产生的很多碎片不能收集，影响了测量的效率；如果太近，虽然测量碎片的立体角比较大，但由于每个探测单元相对于靶子张开的立体角也会增大，造成2个碎片进入同一探测单元的几率增加，这种情况下通过实验无法区分是否为不同的碎片，也就得不到原子核的激发能；此外每个碎片的测量位置误差会增大，造成回推的原子核激发能误差也增大.

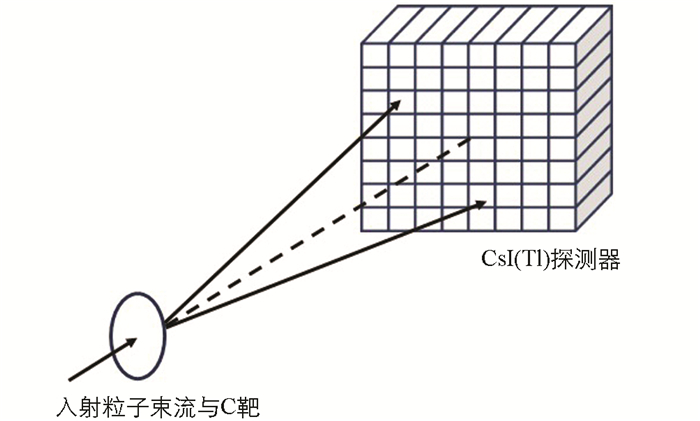
据此本文采用蒙特卡罗方法编写程序模拟分析了测量¹⁷C的结团结构的实验. 实验过程为¹⁷C束流轰击C靶后被激发到结团结构，然后发生碎裂反应. 入射粒子¹⁷C的能量采用真实实验中使用的44.9 MeV/u，在碰撞过程中，反冲靶核和出射的处于激发态的¹⁷C在C系内由各个出射角度同概率发射.

处于激发态的¹⁷C碎裂后，2个碎片在其自身的C系内向各个方向均匀发射. 据此，本文分析了刘平萍等^[19]实验研究的¹⁷C碎裂反应，下面以¹⁷C→¹¹Be+⁶He反应道为例进行模拟计算. 考虑到实验中利用放射性束流作为入射粒子，所以本文对入射粒子的能量进行了涨落考虑，所选定的能量属于高斯分布(标准差为1 MeV/u，即入射粒子的能量存在约为1 MeV/u的能量涨落)；同时入射粒子的入射角度也考虑了具有一定的涨落分布.

由于实验组的闪烁体探测器是由8×8的CsI(Tl)闪烁体单元组成^[20](图 2)，每个探测单元不具备位置分辨的能力，各单元之间因为机械安装的原因有着1 mm的缝隙，那么碎片的落点就会出现以下几种情况：① 2个碎片落到不同探测单元上；② 2个碎片落到同一探测单元上；③只有一个碎片落到探测单元，另一个落在探测单元外；④ 2个碎片都落在探测单元外. 只有在第一种情况下，才可以用获取的实验数据回推出要研究的原子核的激发态，属于有效的实验数据；另外几种情况则不可以，属于无效数据.

当碎片从探测单元的非中心位置进入时，只能代入其所在单元的中心位置进行计算，就会造成碎片发射角度的误差，进而使得测得的激发能会有一定的偏差. 本文有必要通过模拟计算该情况对测量结果影响的大小.

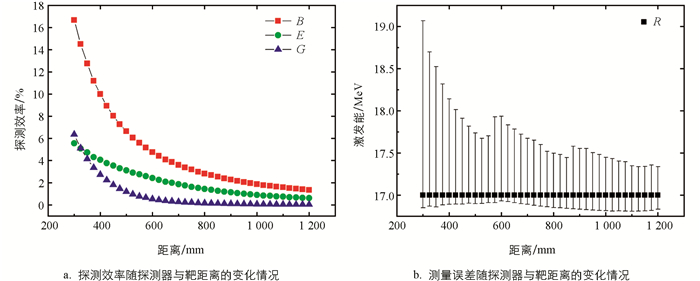
从图 3a可以看出，当¹⁷C激发能为17 MeV时，探测器的摆放距离不同导致碎片收集效率的变化情况. 其中正方形点表示在不同探测距离上2个碎片都落在阵列探测器范围内的入射粒子数与总的入射粒子数的比值B；圆形点表示最终能够通过2个碎片的信息回推出原子核激发能的粒子数与总的粒子数的比值E；三角形点表示2个碎片打到同一块探测单元的粒子数与总的粒子数的比值G. 随着距离靠近，由于探测器相对于出射粒子所覆盖的立体角变大，所以进入探测器的粒子数会更多；但随着距离进一步靠近，2个碎片同时进入同一探测单元的几率也在增加，且最终碎片进入不同探测单元的几率也会随着距离的靠近而增加. 这是因为进入探测范围的碎片数目增加量比2个碎片进入同一探测单元的数目要多一些.

此外还需要考虑用测量到的碎片回推出激发能随探测器与靶距离的变化情况. 图 3b为测量计算出的¹⁷C激发能的误差，图中正方形点表示探测器与靶在不同距离上用测量到的碎片回推出的激发能误差R. 误差棒上下分别表示当前探测器与靶的距离下，激发能回推出的最大值和最小值. 可以看出，回推出的能量与实际入射能量会有误差，且上部的误差要大于下部的误差. 误差来源于2个碎片出射夹角的确定. 进入探测单元的碎片大概率不在探测器的中心位置，但根据碎片的能量和位置回推入射粒子能量只能代入探测单元的中心位置，造成回推入射粒子能量时碎片之间的出射夹角与实际有差异，从而产生误差. 出射2个碎片位置的确定都可能因为探测器颗粒度的大小而产生误差. 通过模拟发现，当2个碎片发射方向均背离2个探测单元中心位置时，得到的碎片之间的发射夹角要小于实际的夹角，结果是回推得到的能量小于实际入射能量. 其他大部分情况下都是得到的角度要大于实际出射的角度，造成回推的入射粒子的能量大于实际入射粒子的能量，因此造成了误差棒的上部要大于下部，且误差随着距离的靠近也在快速地增加，甚至可以达到2 MeV以上. 这样得到的激发能谱是不可接受的，也不可能正确地分析出原子核的结构. 随着探测器与靶的距离增大，2个碎片打到同一探测单元的情况会降低，得到的激发能分辨率也会增加，数据的准确性相对较高，但相对的总探测效率会降低. 实际实验中还要考虑到探测器工作时必须放置在真空腔体中，所以受实验环境以及成本的限制，距离也不宜过大.

本文综合考虑实验中的距离选择为975 mm，从图 3b可以看出在这个距离上计算出的激发能误差较小，其误差最多也不会超过0.4 MeV，即探测单元的颗粒度对实验结果造成的误差相对较小，因此得到的实验结果应该是可信的.

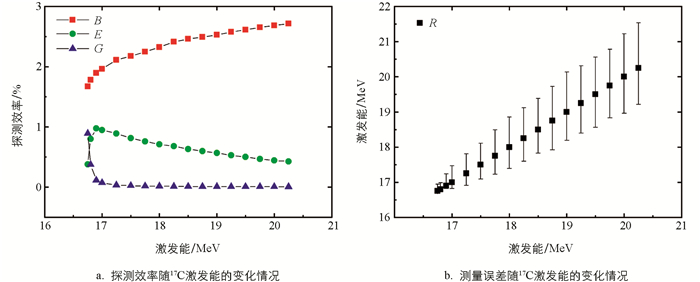
实验最终要得到的激发能谱能量分布比较宽，所以还必须考虑在不同激发能下的测量效率及能量分辨情况. 本文通过模拟计算在具体实验设置的距离上不同激发能的影响，如图 4所示. 根据能量守恒可知，所分析的反应道只可能发生在¹⁷C激发能大于16.75 MeV以上. 本文计算了激发能从16.8 MeV到20.5 MeV这段范围. 其中正方形点表示进入探测范围与入射粒子数的比值随激发能的变化；圆形点表示有效探测的粒子数与总的入射粒子数比值随激发能的变化；三角形点表示2个碎片进入同一探测单元与总入射粒子数的比值随激发能的变化. 从图 4a可以看出，随着激发能的增加，进入探测器探测范围的粒子数量也在逐渐增加，2个碎片进入同一探测单元的概率迅速减小. 最终可以探测到的有效粒子探测效率从开始激发能比较低的地方，探测效率快速增加；随着激发能的增加，到激发能超过17 MeV时达到最大，然后又开始缓慢下降. 从图 4b可以看出，随着激发能的增加，测量误差处于一直增大的趋势. 因此测量得到的数据在低激发能部分的误差较小，可以用于分析原子核的结团结构；但高激发能区数据的误差偏大，所以应该舍去. 如果对更高的激发能感兴趣，则需要在以后的实验中进一步增大探测器与靶的距离.

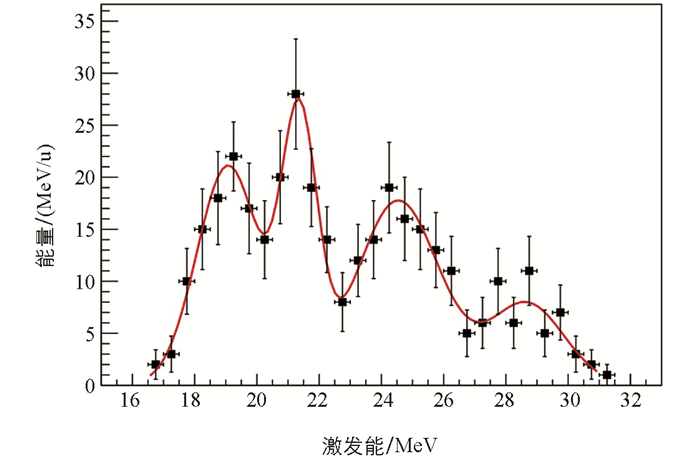
通过对不同探测器距离的分析可知，目前的设置基本上可以实现实验目标，得到的实验数据是可信的. 图 5是实验中通过测量¹¹Be和⁶He的碎片，得到的¹⁷C激发能谱，并对获得的实验数据进行了并道和分析，给出了误差棒，可以清晰地看出有峰存在，具体的原子核结构信息还需要进一步分析和处理.

转移反应是选定某一原子核作为入射粒子与靶子反应，发生了1个或多个核子的转移，生成了要研究的原子核并处于存在结团结构的激发态. 该原子核碎裂后，通过对碎片的测量，可以回推出原子核的激发态. 与碎裂反应不同的是，转移反应的入射粒子能量要求比较低，只需超过库伦位垒不多即可，一般情况下转移反应的截面比碎裂反应要大得多，但因为C系的速度较低，所以碎片的分布比碎裂反应更弥散一些，碎片的测量效率要低一些. 同时，要得到原子核的激发态，还必须测量出反冲靶核的信息. 所以一般采用多套探测装置，分布在不同的角度，用于测量不同的碎片和反冲核，以便获得更好的实验结果.

同样采用蒙特卡罗方法对转移反应进行了研究. 原子核的激发过程与前文相似，但是靶核A与反冲核B不同，入射粒子a与出射粒子b不同，b是要研究的处于激发态的原子核. b碎裂后，碎裂成2个不同的碎片，除了要测量碎片外，还要测量反冲核B的信息，然后才可以计算出b的激发能. 本文对¹⁴C结团结构的转移反应实验^[13]进行了研究. 该实验中探测装置由U0、D0、U1、D1、U2和D2这6套探测器组成. U0和D0位于Be靶140 mm处，相对于束流方向呈±23°，用于探测¹⁴C碎裂后的碎片；U1和D1位于Be靶116 mm处，相对于束流方向呈±60°；U2和D2位于Be靶114 mm处，相对于束流方向呈±109°. 其中U1、D1、U2和D2用于探测反冲核. 实验中，入射粒子的能量选择为5 MeV/u，激发过程的反应方程为：

碎裂过程选择的反应道为：

其中：α₁为反冲核；碎裂后的α₂为α粒子碎片，简称为α粒子.

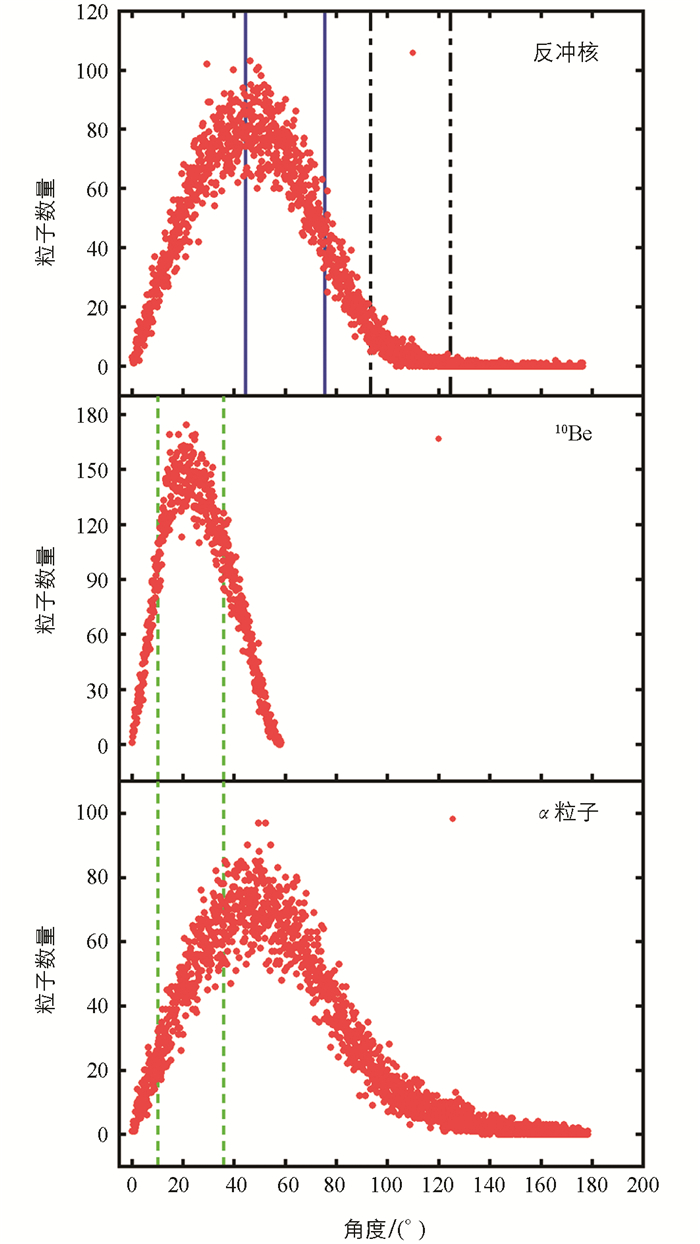
以¹⁴C激发能为15 MeV为例，首先计算碎片和反冲核在L系的角分布(图 6). 可以看出，反冲核的分布范围较大，但也主要分布在前角区. 实验中采用了3套探测器进行测量，但后角区的探测器对效率的提升不够明显. 图 6中蓝色和黑色线的范围代表了测量反冲核的U1、D1、U2和D2的探测范围. 建议后续实验中可以将U2和D2探测器再向前角区放置，以便提高收集反冲核的效率. 对于碎片的测量，由图中探测器的覆盖角度可知，该实验中的探测器U0、D0对碎片¹⁰Be的收集效率是最高的，但此时碎片α粒子的收集效率并不太高. 因为必须同时测量到2个碎片才是有效的实验数据，所以此时的探测器设置并不是最佳的位置.

同时还要考虑当¹⁴C激发能变化时，测量效率的变化. 首先考虑测量反冲核的U1、D1、U2和D2位置不变，只改变实验中测量碎片的U0和D0探测器的摆放角度，观察收集碎片¹⁰Be和α粒子的效率变化，如图 7所示. 当U0、D0摆放角度变换时，碎片的收集效率变化也比较大. 随着探测器摆放角度从0°逐渐增加时，收集效率也逐渐提高；但增加到一定的角度后，收集效率会随着角度的增大而降低. 摆放位置相对于束流方向呈±31~33°时，探测器的收集效率是最高的，比实验中的摆放角度±23°时的收集效率提高了约40%. 但综合考虑到实验中各个探测器的覆盖角度不可重复，因此U0、D0的摆放角度在31°，收集反冲核的U1、D1、U2、D2的摆放角度在60°及以上时，能够最大程度提升收集效率.

结团结构是目前原子核物理研究的热点，但实验研究相对来说难度比较大，主要存在反应截面偏小，探测器的性能指标要求比较高等原因. 在有限的实验条件下，如何提高测量效率是所有实验工作者都非常关心的问题，本文对此进行了系统地研究.

首先研究了不同入射情况对探测结果的影响. 通过对不同入射角度、位置和能量的入射粒子进入同一闪烁探测单元进行模拟，发现不同情况下探测单元给出了相同的光子收集效率，保证了获取的数据与测量的粒子能量成正比. 说明以闪烁体探测器进行测量的合理性，可以给出科学的实验结果.

同时还分析了原子核的激发过程，为进一步碎裂后通过测量碎片回推原子核的激发能谱提供了理论依据. 对于测量结团结构的2种方法——碎裂反应和转移反应的实验方法，本文均通过蒙特卡罗进行了模拟研究. 模拟过程中，为了与真实实验过程更接近，本文对入射粒子还考虑了能量和入射角度的涨落，并与具体的实验过程进行比较.

对碎裂反应的模拟：以本课题组¹⁷C实验为例，对探测器的探测效率和回推实验结果的误差进行了分析，说明了本文得出的实验结论是科学和可信的.

对转移反应的模拟：以北京大学实验组¹⁴C实验为例，分析了探测器的摆放位置对最终收集效率的影响. 发现该实验的探测器摆放设置并不是最佳的位置. 如果按照本文计算的最佳位置开展实验，探测效率至少可以提高40%，这对实验是非常有意义的. 后期的实验过程中将根据目前的模拟方法进行仔细分析，以期获得最佳的实验效果.