-
开放科学(资源服务)标识码(OSID):

-
有载分接开关(On-Load Tap-Changer,OLTC)作为变压器唯一可动的机械结构零部件,负责变压器带负载条件下改变分解绕组位置进而实现电压调节功能,其运行可靠性与电网供电稳定安全息息相关[1-3]. 但随着电网结构日益复杂以及服役时间增加或出厂缺陷等原因,导致OLTC机械故障频发,比如紧固件松动、机械卡涩、弹簧疲软断裂等故障[4]. 为了及时发现OLTC机械故障,保证电力系统供电安全稳定,有必要开展对OLTC机械故障诊断方法的研究. 尽管OLTC内部参与调压切换的机械结构复杂,但在进行切换时主要的零部件状态信息均可在检测到的振动信号波形中体现出来,例如槽轮制动异常产生开关滑动的故障导致出现2个振动脉冲,弹簧弱化导致振动峰值减小,驱动机构润滑不足导致振动波形出现毛刺现象[4-5],因此基于振动信号的OLTC工况识别研究成为当前研究热点. 对OLTC振动信号进行分析不难发现,内部机械结构状态信息分布在多频率尺度上,因而选用合理、高效的特征提取方法成为OLTC故障诊断的关键点[6-7].
近年来,随着自适应分解方法在非线性信号分析领域的广泛应用,许多学者提出了基于递归分解原理的非线性信号模态分解方法并应用于OLTC特征提取. 阳瑞霖等[8]采用EMD对原始OLTC振动信号进行模态分解,并选取前5个本征模态分量的能量特征作为SVM的输入样本对其机械故障进行诊断研究. 传统EMD虽能够自适应分解非线性信号,但是在分解过程中多次采用三次样条插值拟合,导致端点极值包络线发散从而使信号失真(端点效应),以及在求解包络时局部极值点在短时间内发生多次跳变,导致特征时间尺度划分不准确引起的子模态分量中心重叠现象(模态混叠)[8-10]. 杨波等[10]向原始信号中加入高斯白噪声减小局部极值间距来解决EMD分解模态混叠的问题,这便是互补集合经验模态分解(CEEMD)方法. 目前也有学者利用该方法对OLTC振动信号进行分析研究,但该方法仍难以对OLTC进行有效分解[11-12]. 随着Dragomiretskiy等[13]提出基于非递归分解的变分模态分解方法,该方法能够在不丢失原始信号特征情况下,自适应更新各模态分量(IMF)的最优中心频率以及带宽,在处理非线性稳定信号方面得到了广泛的应用[14]. 上述几种方法虽然在OLTC振动信号模态分解领域得到了广泛的应用,但都有模态分解时产生虚假分量、特征提取不完整等问题,从而导致OLTC故障模式识别存在误差.
目前针对基于振动信号的OLTC故障诊断主要有聚类分析、人工神经网络、隐马尔可夫模型、支持向量机(SVM)等模式识别算法. 周翔等[15]基于相空间重构法并利用K-means聚类法能够有效识别OLTC的故障隐患,但是相空间重构后样本维数增加导致计算量增大. 上海交通大学的曾全昊团队基于OLTC振动信号的相空间分布构建距离映射递归图作为CNN的特征输入,其训练的人工神经网络模型对OLTC故障模型具有良好的识别性能,对于轻微故障的识别表现出优异的识别准确率[16-18]. SVM自身的算法学习能力强,具有优异的泛化性以及鲁棒性被逐渐引入OLTC振动信号模式识别领域中[7].
针对OLTC状态特征提取不完整导致故障诊断识别准确率低的问题,本文提出了基于大白鲨(WSO)算法优化VMD参数模型和样本熵的OLTC振动信号特征提取方法,并利用SVM对OLTC不同工况进行分类识别. 首先以IMF的最小包络熵作为目标函数,利用WSO优化VMD中的参数K和a,获得OLTC不同工况下振动信号最优分解VMD模型. 利用优化后的VMD模型对OLTC振动信号进行分解获得IMF分量,并利用IMFs分量求解样本熵构建样本特征向量. 最后利用SVM对OLTC运行工况进行分类识别. 实验结果表明:相比于传统模态分解以及经验确定VMD模态分解法,WSO-VMD法能够提取更丰富的OLTC内部机械零部件工作状态特征参数,并且搭建的SSA-SVM算法模型对OLTC不同工况表现出了优异的识别准确率.
全文HTML
-
VMD分解的本质是通过寻找一组子模态分量并限制其中心频率和带宽,以实现非线性信号的自适应分解. 该分解法将经典维纳滤波器推广至多个适应波段,并采用交替方向乘子法对变分模型进行有效优化,使其对采样噪声的鲁棒性更强. VMD以模态分量中心频率带宽ωk之和最小以及模态分量之和等于原始信号为约束条件,将原始信号分解为不同频率段的K个子模态,其约束方程如下:
式中:K为模态数;uk为模态分量;wk为各模态分量对应中心频率. 引入惩罚因子a以及Largrange算子λ,将变分约束问题转化为非约束性问题进行求解. Largrange函数为:
采用交替乘子方向法(Alternate Direction Method of Multipliers,ADMM)对ukn+1,ωkn+1,λkn+1进行迭代优化,为求解Largrange鞍点,采用如下步骤:
步骤1 初始化{uk1},{ωk1},λk1以及令n=0;
步骤2 利用下式对{uk1},{ωk1},λk1进行更新:
步骤3 重复步骤2直至满足迭代条件:
式中:ε为判别精度.
步骤4 获得K个模态分量.
在对OLTC振动信号进行模态分解时,其分解个数K和惩罚因子a的选择决定着分解效果. K值过大,则会造成原始信号过分解而产生虚假分量;反之K值过小,则会造成信号分解不彻底,使模态分量中心频率重叠,无法分解出主要频率信号. 为了准确提取原始振动信号中丰富的特征信息,本文采用WSO算法对VMD进行参数寻优.
-
大白鲨优化算法是Braik等[19]在2022年根据大白鲨跟踪和捕食猎物的行为特征而提出的新型群智能优化算法. 该算法全局搜索能力强、参数少,具有较强的鲁棒性和适应性,被广泛运用于参数寻优. 大白鲨有着敏锐的嗅觉、听觉以及对猎物游动水波的感知,使其更加快速锁定猎物位置. 大白鲨捕猎行为分为以下3种:
① 包围猎物:大白鲨依靠自身听觉、嗅觉以及感知猎物移动产生的水流波动,向猎物靠近.
② 搜寻猎物:为了防止寻优过程中陷入局部最优,大白鲨种群还会在搜索空间内的边界附近进行随机搜索.
③ 捕食猎物:鲨群会向最佳捕猎位置靠近.
在进行VMD参数优化前需要对大白鲨种群进行参数初始化,包括大白鲨种群数量N、搜索空间维度d、最大迭代次数T以及种群初始位置X=(x1,x2,…,xi). 其中大白鲨种群xi=[ai,bi]中,ai和bi分别表示搜索空间的上界和下界,第i条大白鲨在第j维(j=1,2,…,d)的初始位置由下式定义:
式中:r表示[0, 1]之间的随机数.
根据大白鲨捕猎行为①可知,大白鲨会根据猎物移动产生的气味、水流波动来感知猎物方向,并以速度v向猎物进行移动,其速度更新如下式所示:
式中:t表示大白鲨位置更新次数;vti表示迭代t次时第i条大白鲨的速度;xgbest和xbest分别表示大白鲨种群全局最佳位置和第t次迭代的大白鲨种群中第i条大白鲨的全局最佳位置;r1和r2表示[0, 1]之间的随机数;vk+1i表示下一次迭代过程中第i条大白鲨的速度,设置v0i;p1和p2分别表示大白鲨种群运动控制参数,其计算如下式所示:
式中:pmin和pmax分别表示大白鲨最佳运动状态下的最小速度和最大速度.
依据大白鲨搜寻猎物行为机制进行位置更新,在区域边界附近进行搜索,防止进入局部最优. 在行为①和行为②中,其位置更新表达式如下式所示:
其中:┐表示负运算符;⊕表示向量的逐位异或运算;a和b表示搜索空间的上下界限;rand表示[0, 1]之间的随机数;f表示波浪的频率;参数mv表示大白鲨嗅觉、听觉灵敏度,其参数设置决定了大白鲨算法的全局以及局部搜索能力,其计算如下式所示:
式中:常数a0和a1分别用于决定WSO探索和开发能力. mv设置过大将导致进行全局搜索,搜索次数变多;反之过小将导致进行局部搜索,搜索强度变大,但也容易陷入局部最优.
大白鲨通过行为特征③向最佳鲨群位置移动,其位置更新如下式所示:
其中:
$ \tilde{\boldsymbol{x}}_{k+1}^{i}$ 为第k条大白鲨在经过下次迭代后相对于猎物的位置向量;r1,r2和r3分别为[0, 1]范围内的随机数;Dw为猎物与大白鲨之间的距离向量;S表示大白鲨靠近最优猎物位置时的嗅觉和视觉强度. 其他大白鲨根据鲨群行为向最优位置运动,其最终位置位于搜索空间内最优猎物位置附近.在利用WSO对VMD进行参数寻优时,需要选取合适的适应度函数用于评估变分模态分解效果,本文采用唐贵基等[18]提出的包络熵作为评判标准. 包络熵可用于表征OLTC振动信号的中特征信息量,当信号中的特征信息被噪声信息淹没时,则包络熵值较大,反之则较小. 长度为N的时间信号x(i)经Hilbert解调得到包络信号a(i). 为了避免模态分量之间包络幅值的不同影响以及增强抗干扰能力,需对a(i)进行归一化处理,随后依据信息熵计算规则获得包络熵Ep,其计算如下式所示:
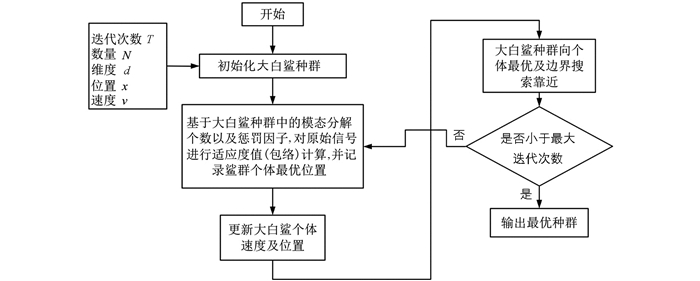
WSO-VMD算法的整个计算流程如图 1所示.
-
熵值是用于表征信号序列复杂度、信息量以及不确定性的无量纲指标,熵值越大则代表信号越复杂. 研究人员为了度量时间序列产生新模式的概率大小提出样本熵算法,该方法适用于非线性信号中不稳定冲击性信号的特征表达. 样本熵值大小与时间序列复杂度正相关,而对OLTC振动信号分析不难发现,由于OLTC切换时内部机械部件的突然性动作导致其振动波形大多表现为冲击性,因此利用样本熵表征OLTC的故障特征是有效的. 虽然样本熵有着和近似熵一样的物理意义,但是样本熵的计算不依赖时间序列长度,具有更好的一致性以及普适性,抗干扰能力也优于近似熵,因此选择样本熵对OLTC振动信号的模态分量构建特征向量. 对于N个数据构成的时间序列{x(1),x(2),…,x(N)},其序列样本熵的计算步骤如下所示:
步骤1 将原始信号重构为m维向量序列Xm(1),…,Xm(N-m-1),其中Xm(i)={x(i),x(i+1),…,x(i-m+1)},1≤i≤N-m+1,也可理解为采用窗长为m、设置步长为1对原始序列进行采样重构.
步骤2 定义d[Xm(i),Xm(j)]为不同向量之间最大差值的绝对值,即:
步骤3 对于i,j∈[1,N-m]定义距离r,对于给定Xm(i),统计其与Xm(j)中距离小于等于r(相似容限)的j的数目并记为Bi,定义:
步骤4 定义B(m)(r):
步骤5 增加序列重构维数到m+1,按照上述步骤计算出:
由上述步骤可以求得B(m)(r)和A(m)(r)分别是2个序列在相似容限r下匹配m以及m+1个点的概率,由此可得序列的样本熵(SampEn):
-
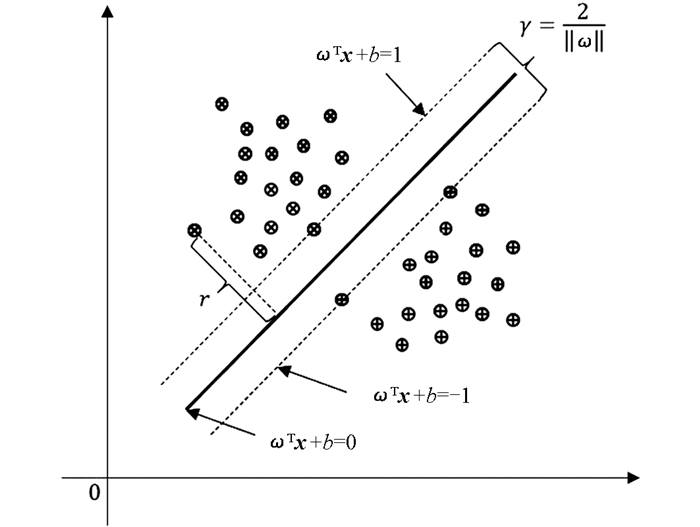
基于OLTC样本熵特征量样本数较小且均为非线性的特点,因此本文选用SVM对OLTC进行状态模式识别. 对于给定数据集{(x1,y1),…,(xi,yi)},i=1,2,…,l,其中x为数据样本特征,y为样本标签. 对于多维特征,SVM构造超曲面f(x)=ωTφ(X)+b对输入样本进行划分,ω定义为平面权向量,b为偏差,其原理示意图如图 2所示.
为了提高样本分类的准确性,需要对超曲面进行最优求解,依据原理示意图构造约束条件:
但常见样本特征多为线性不可分的情况,因此需引入松弛变量ξ=(ξ1,…,ξi)T (ξi>0)来提高模型对噪声和异常点的容忍度,并提高泛化能力. 加入松弛变量后其约束条件如下式所示:
式中:C为惩罚因子,即给分类误差加入代价函数. 引入Largrange函数以及参数ai和ai*求解凸规划问题:
式中:ai>0,ai*≥0. 根据KT条件,求解最优超平面的充分必要条件为:
由上式可将优化问题转换为对偶问题求解出最优超平面:
常利用核函数K(x·y)=ϕ(x)· ϕ(y)代替线性、多项式核函数(x·y).
但是SVM模型中包含了2个关键参数C和g,参数C用于表示模型对输入样本误差的包容度,g为SVM的核参数,决定新的特征空间中数据位置的分布情况. 2种参数的选择均会影响SVM的训练结果,因此也需要对SVM的参数进行参数寻优,从而提高OLTC故障识别的准确率.
1.1. 变分模态VMD分解原理
1.2. 基于大白鲨WSO算法的VMD参数优化
1.3. 基于样本熵的OLTC振动信号特征向量构建
1.4. 支持向量机SVM算法原理
-
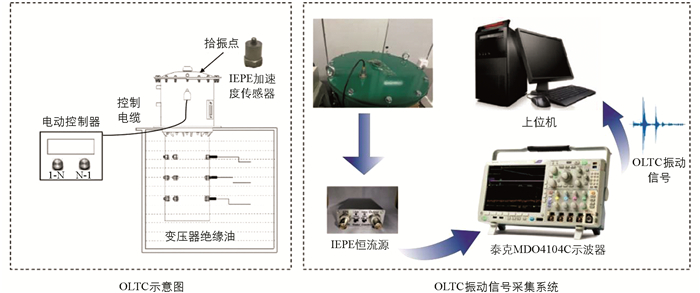
本文搭建了OLTC故障模拟实验平台以及振动信号检测系统(IEPE加速度传感器、恒流源、信号采集器以及信号分析软件Matlab 2020),开展了基于振动信号的OLTC故障诊断研究,其信号检测平台设计如图 3所示.
选取双城国开公司的SYJZZ-10 kV型复合式OLTC作为实验对象,该分接开关采用三相直接切换、中部跨接式进行调压,额定电流为100 A,开关各触点接触电阻小于等于500 μΩ,整个开关电动操作切换一次时间为12 s,其中过渡电阻切换时间为15~35 ms,可通过自动或电动控制器实现精准快速调压. 当OLTC进行分解绕组切换时,内部电动机从电动控制器获得调压指令后开始转动,经两级蜗轮蜗杆减速机构减速后推动铆在涡轮上的圆柱销转动;圆柱销推动拐臂转动,使拉伸弹簧逐步拉伸储能直至弹簧机构过死点释放,带动拨槽件转动,使槽轮转过一个等分,便完成了变压器挡位的切换. 振动传感器选用YK-YD55型压电式加速度传感器,其相关参数如表 1所示. 恒流源选用凌航公司生产的单通道IEPE恒流源,频率带宽为0.3 Hz~100 kHz,采用24 V直流供电,其输出电流为4 mA,增益挡位有“×1”和“×10”2个挡位选择,性能稳定,抗噪能力强,可有效输出传感器采集到的加速度电压信号. 泰克MDO4104C示波器拥有20 Mpointe记录长度,在获取长时间段的信号后仍保持较高的分辨率;拥有4个模拟通道、1 GHz带宽以及高达5 GS/s的采样率,能够准确采集OLTC的振动信息.
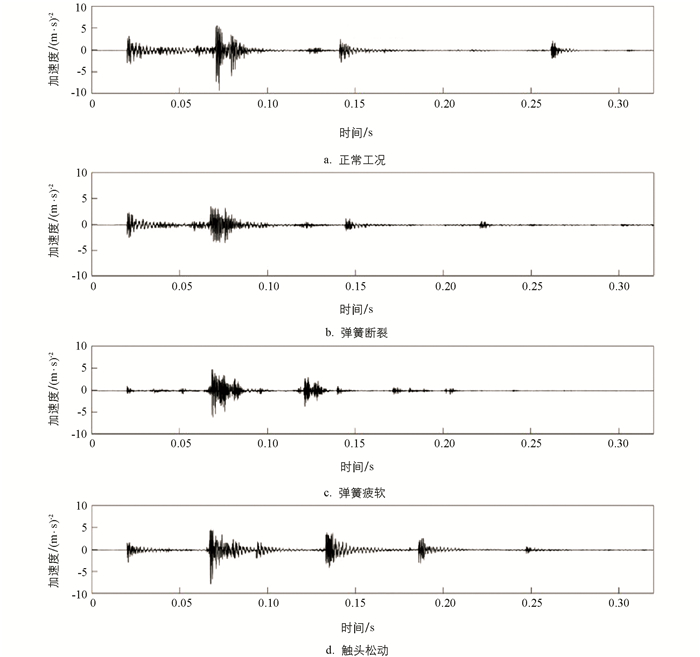
本文设计OLTC正常工况以及3种典型缺陷的模拟实验,如图 4所示. 其中:1) 去掉一根主弹簧用于模拟弹簧断裂故障;2) 选用劲度系数较小的弹簧并将其弯曲处理用于模拟弹簧疲软故障;3) 松动固定触头螺母用于模拟触头松动故障. 设置示波器采样频率为40 kHz,OLTC正常、弹簧疲软、弹簧断裂以及触头松动下的4种振动信号如图 5所示.
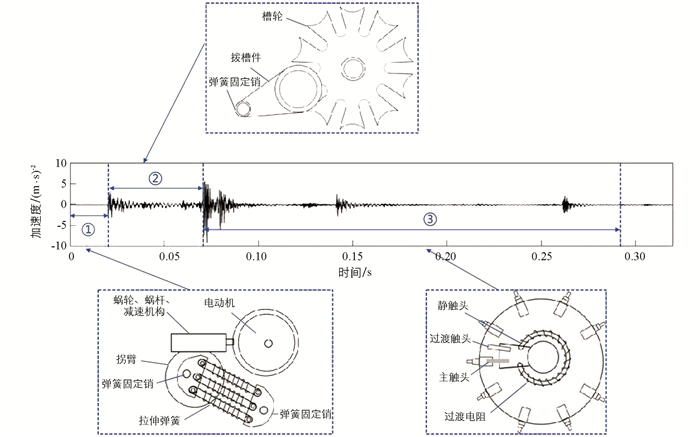
基于OLTC振动波形以及内部机械结构先后动作时序可以将其分为3个阶段,如图 6所示. 第1阶段为弹簧经由电动机拉伸储能,这期间主要由弹簧、电机以及蜗轮蜗杆减速机构产生微弱振动信号,在此阶段中无明显振动波形产生;第2阶段为弹簧经过死点释放至动静触头碰撞之间的振动信号,此阶段的振源主要来自弹簧的突然动作以及储能弹簧带动拨槽件转动与槽轮产生的碰撞,可以看出弹簧以及槽轮突然动作产生了较为明显的冲击性波形;第3阶段为拨槽件带动下方动触头与静触头猛烈碰撞产生振动能量,此阶段的振源来自动静触头碰撞以及内部齿轮机构的突然停止,随后振动信号能量随时间逐渐变小直至趋于0. 可以看出,当OLTC内部机械零部件改变其原始运动状态时,便会产生较为剧烈的振动波形,并且由于零部件运动状态的改变时间极短,振动波形多具有冲击性,并且随着时间的推移波形逐渐减弱. 通过图 5中OLTC不同工况下的振动信号分析可以看出,与正常工况相比,弹簧断裂故障下由于弹簧储存的弹性势能变小导致动静触头碰撞产生的振动能量有所减弱;弹簧疲软故障下,由于弹簧进行拉伸弯曲处理导致弹簧释放产生的振动较小,并且弹簧释放完之后仍会产生振动现象;触头松动故障下,动静触头发生碰撞后由于触头松动导致撞击后产生少量的余振现象. 综合分析可以看出OLTC内部主要的机械结构部件性能可以间接由振动信号波形呈现出来.
-
针对传统模态分解法对OLTC故障振动信号特征提取不完整导致诊断识别准确率低的问题,本文选用WSO-VMD算法获得不同工况下振动信号最优分解参数组合[K,α],再利用寻优后得到的VMD模型对振动信号进行分解处理获得对应K个IMF分量,之后求取其对应样本熵值并构建OLTC不同工况下的特征向量,作为SVM的输入进行OLTC故障诊断. 在利用WSO优化时设置搜索空间维度为2,种群数量为10,迭代次数为20以及惩罚因子α和K的上下限分别为ub=[2 300,15]和lb=[100, 3],WSO的参数设置如表 2所示. 在寻优过程中将最小包络熵作为目标函数[20].
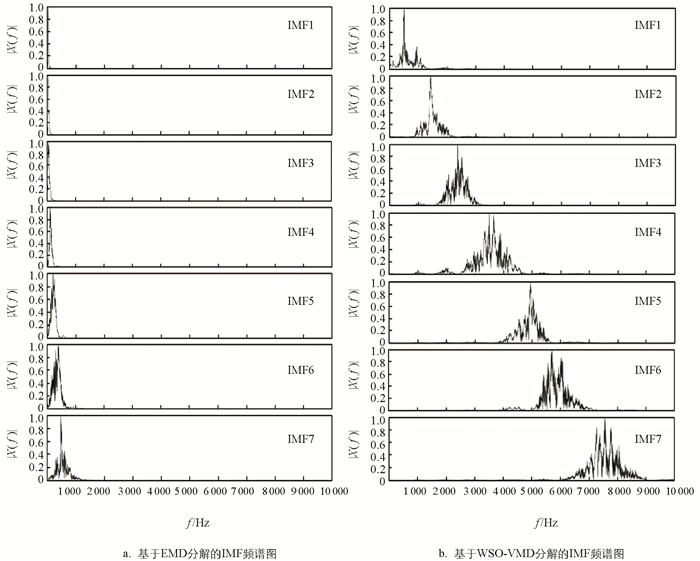
为了更好地对比分解结果,分别利用参数优化后的VMD模型以及EMD对OLTC正常工况振动信号进行模态分解并计算各模态分量归一化频谱图. EMD模态分解以及WSO-VMD模态分解获取的IMF数量分别为14和10,本文选取前7个模态分量作为比较对象,其对应模态分量的频谱图如图 7所示.
对比传统EMD以及WSO-VMD方法对OLTC振动信号进行模态分解的模态分量频谱图可以看出,EMD分解获得的模态分量在低频段内发生了严重的中心频率混叠,即EMD无法对OLTC振动信号进行有效分解,这也证明了由于OLTC内部机械结构复杂,导致提取到的振动信号中存在异常事件影响了OLTC极值点的选取,使极值点分布不均匀造成模态分量中产生了异常分量. 对比EMD与WSO-VMD对OLTC振动信号分解的IMF频谱图可以看出,相较于EMD分解,本文选用的WSO-VMD方法得到的OLTC振动信号模态分量并未产生混叠现象,能够有效获取其振动信号不同频率段的故障特征. 针对OLTC 4种不同工况下的振动信号,本文利用WSO算法分别对不同工况下10组振动信号的VMD分解参数进行寻优并求取平均值,其最优参数组合[K,α]如表 3所示.
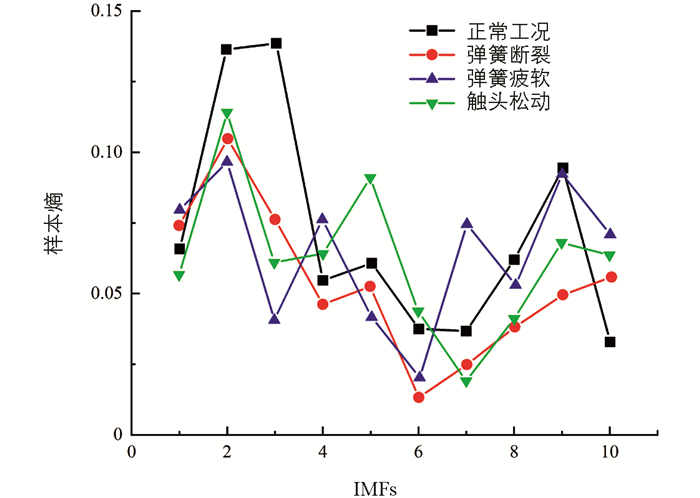
利用WSO优化VMD模型对OLTC不同工况振动信号进行模态分解获取对应IMFs,每种OLTC工况选取其中10组振动数据进行模态分解获取对应模态分量,对模态分量进行样本熵计算并求取均值,结果如图 8所示. 从图 8可以看出不同工况下的样本熵特征存在差异,这是因为OLTC不同工况下,其内部机械零部件性能具有明显差异,这种差异可以反映至检测到的振动波形中,最后导致VMD模态分解计算的不同模态分量以及对应样本熵值存在着差异.
-
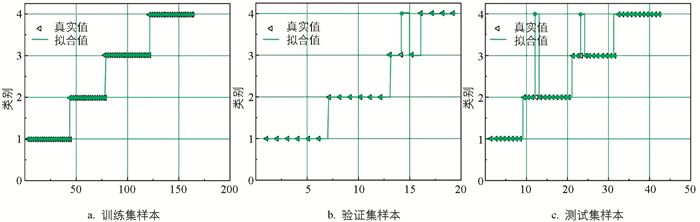
根据最优VMD参数模型对OLTC不同工况下进行模态分解,选取前10个模态分量的样本熵构建样本特征向量. 为了证明该方法的鲁棒性与可靠性,本文选用同种型号的不同OLTC故障模拟实验并进行振动信号采集,选取4种工况各60组样本(每个OLTC采集12个振动信号样本)作为数据集,共计240组实验数据. 依据数据样本以7∶1∶2的比例构建样本训练集、验证集以及测试集进行SVM分类训练,训练过程中采用监督式训练,以标签1、2、3、4分别对应OLTC正常工况、弹簧断裂、弹簧疲软以及触头松动4种不同的状态结果. 利用SVM对OLTC运行状态进行特征分类,其训练时间为0.421 s,训练集、验证集以及测试集结果如图 9所示.
基于WSO-VMD以及样本熵构建的OLTC工况特征向量,利用SVM对OLTC不同工况进行分类,从训练结果可以看出:训练集样本的分类识别准确率为100%,而验证集以及测试集的识别准确率均为95.83%,平均识别准确率为98.75%,表现出了对OLTC故障工况优异的识别准确率. 为验证优化后的VMD分解模型对OLTC振动信号模态分解的有效性和准确性,利用给定参数VMD(K=10,a=2 000)、EMD和EEMD分解对OLTC振动信号进行模态分解,并用样本熵对OLTC不同工况进行特征向量构建,选用SVM进行模式识别,其不同模态分解方法的测试集识别准确率如表 4所示.
由图 9和表 4可以看出,相较于其他特征提取方法,SVM对本文提出的WSO-VMD模态分解法构建的特征向量拥有更高的识别准确率. 此外,SVM对正常工况以及弹簧断裂2种工况的识别准确率高于弹簧疲软以及触头松动故障,这是由于OLTC弹簧疲软以及触头松动2种工况相对于正常工况,故障设置改变并不是很大,因此其原本机械结构并未发生较大的变化,同时也体现在检测得到的振动信号波形与正常波形之间的差异性较小. 而弹簧断裂对OLTC内部机械结构改变程度相较于弹簧疲软以及触头松动2种工况较大,因此弹簧断裂对应振动波形与正常工况之间的差异性也较大,对OLTC故障诊断识别准确率最高. 通过不同OLTC特征向量构建方法的结果对比可以看出,其测试集准确率比EMD、EEMD以及给定参数VMD分别提高了9.52%、4.54%以及2.22%,这也表明本文提出的WSO参数优化VMD法能够提取更为丰富的OLTC内部机械特征. 为进一步提高SVM对OLTC故障识别的准确率,选用粒子群(PSO)、麻雀搜索(SSA)以及灰狼优化(GWO)算法对SVM进行参数寻优[20-22],并对OLTC不同工况的特征分类进行研究,其测试集分类识别准确率结果如表 5所示.
通过几种优化算法展开SVM参数寻优,不同参数优化SVM模型对OLTC测试集的平均识别准确率均高于95%,特别是对OLTC弹簧疲软以及触头松动2种故障识别的准确率有了明显的提高,均在90%以上. 此外,从表 5中可以看出SSA-SVM算法对OLTC 4种工况测试集样本识别的准确率均为100%,表现出对OLTC优异的故障识别准确率. 通过不同智能优化算法对SVM进行参数优化,其结果表明了本文提出的特征提取法能够提取OLTC丰富的机械状态特征信息,以及训练的SSA-SVM算法能够有效对OLTC进行故障诊断.
-
针对目前基于振动信号分析的OLTC故障诊断中存在着特征提取不完善以及故障识别准确率低的问题,本文系统性提出了基于WSO优化VMD和样本熵的OLTC机械振动信号特征提取方法以及基于SSA-SVM的OLTC故障诊断方法. 首先以包络熵作为目标函数用WSO对VMD进行参数寻优,经参数优化的VMD模型对OLTC振动信号进行模态分解获得模态分量,再利用样本熵构建不同工况的特征向量,并作为SVM的输入开展了OLTC的故障诊断识别研究,其结果表明:
1) 相较于传统EMD以及EEMD模态分解法,本文提出的WSO-VMD分解法对OLTC振动信号分解获得的模态分量不存在中心频率混叠现象,对OLTC振动信号分解效果更好,能够提取OLTC更为丰富的状态特征.
2) 基于WSO-VMD对OLTC不同工况的振动信号进行模态分解获得模态分量,计算模态分量对应的样本熵值并构建特征向量. 利用SVM对样本进行分类识别,其测试集样本分类准确率为95.83%,并且在训练集中的识别准确率为100%,表明本文搭建的SVM分类模型对OLTC表现出了良好的故障识别准确率以及基于WSO-VMD的OLTC振动信号特征提取的有效性.
3) 利用不同模态分解方法开展OLTC振动信号模态分解与样本熵特征向量构建,其SVM分类结果表明:相比于EMD、EEMD与给定参数VMD方法,本文提出的WSO-SVM分解法获得的特征更为丰富,对OLTC故障诊断识别的准确率最高,其测试集准确率比EMD、EEMD以及给定参数VMD分别提高了9.52%、4.54%以及2.22%. 由于OLTC弹簧疲软以及触头松动2种常见故障设置与正常工况差异较小,因此对于这2种工况的识别准确率较其他2种工况低. 此外不同模态分解法对OLTC故障诊断表现出了优异的识别准确率,表明本文利用样本熵作为OLTC不同工况特征向量的可行性以及有效性.
4) 为了进一步提高对OLTC故障识别的准确率,分别选用SSA、PSO以及GWO算法对SVM进行参数优化,结果表明:SVM参数优化之后,对OLTC触头松动以及弹簧疲软2种工况的识别准确率均有明显的提升,并且基于SSA-SVM算法对OLTC 3种故障样本测试集识别的准确率均为100%,表现出了优异的识别准确率.
综合来看,本文提出的基于WSO-VMD模态分解法能够实现对OLTC振动信号的准确有效分解,样本熵也能够提取OLTC丰富的状态特征,并且设计的SSA-SVM算法模型实现了对OLTC故障的准确分类. 本文的研究对于OLTC故障诊断具有一定的工程实践意义与参考价值.



 下载:
下载: