-
开放科学(资源服务)标识码(OSID):

-
第四次工业革命,也被称为工业4.0 (I4.0),在工艺研究领域引起了极大关注。工业革命通常从技术角度来定义:第一次工业革命涉及蒸汽动力系统,第二次工业革命涉及电力系统的使用,第三次工业革命涉及信息技术和自动化。广义地说,工业4.0是指信息技术的进一步数字化和集成,包括物联网、基于云的系统、协作机器人、大数据分析、增材制造和网络物理系统等应用。工业4.0代表了一种革命性的变革,其核心是将物理系统与数字世界相互融合,以实现更高效、智能和自动化的生产过程[1]。首先,工业4.0强调了全面数字化的重要性。现代制造系统不再依赖于传统的模拟控制,而是借助传感器、物联网和云计算等技术实现实时数据的采集和共享。这使得制造系统能够更好地了解其状态,并及时做出反应。其次,工业4.0引入了人工智能(AI)作为制造的关键组成部分。AI技术,包括机器学习和深度学习,已经在工业领域产生了深远的影响。在生产过程中,AI可以用于优化调度、质量控制和故障检测。在产品设计方面,AI可以帮助制造商更好地理解客户需求,并自动生成设计方案。此外,协作机器人和自主机器人已经开始在工厂中执行各种任务,从而提高生产效率。
在制造过程中,产品设计是一个复杂的综合性任务。它涉及从产品概念的形成、结构设计、材料选择、工艺规划,到最终产品的样品制作和测试等一系列环节[2]。特别是在整个产品设计开发流程的初始阶段,需要进行大量调查,以提高产品创新设计成功的可能性。然而,产品设计开发过程中涉及了众多不同的数据和信息源,包括商业案例、市场调研、客户偏好等等。这些数据和信息通常来自多个不同的领域,以及多种不同的形式。传统的工业产品设计方法未能充分利用这些丰富的信息资源,因此,通过研究数据模式和它们之间的关联关系来指导产品设计变得至关重要。在现代工业环境中,工业大数据代表着庞大的数据集,这些数据集蕴含着宝贵的信息,可以用于指导产品设计和开发过程。这些数据可以包括市场趋势、客户反馈、供应链信息、生产数据等等。研究如何有效地利用工业大数据来支持产品设计变得至关重要。这包括了对数据模式的分析、数据间关联关系的挖掘,以及如何将这些信息应用到产品设计过程中。
关联规则挖掘(ARM)是数据挖掘的核心技术之一,旨在从混合数据集中发现潜在有价值的关联关系。然而,在许多产品设计研究中发现商品的数据集之间的关联并不简单。数据集之间有很多重叠交叉点,数据集之间的边界也比较模糊。传统的关联规则挖掘方法无法克服重叠和边界问题。而基于模糊的方法可以管理不确定性,并产生更精确的解决方案。
研究发现,产品设计开发流程的前端对于成功推出新产品至关重要,但复杂性和不确定性容易导致模糊前端(FFE)的发生。大数据环境中的机器学习有望在制造业中实现工业智能,以促进产品设计中的FFE。当考虑模糊性时,特别是FFE,模糊推理系统被认为是可行的,可以通过分析清晰和语言变量来提供模糊决策支持。模糊推理是一种使用模糊逻辑进行推断或决策的过程。它将模糊逻辑的原则和规则应用于具体的问题,以根据模糊输入数据生成模糊输出结果。模糊逻辑是人工智能的一个子领域,被称为多值逻辑。它提供了一种描述模糊性概念的可靠方法。在模糊逻辑中,每个语句都有0到1之间的隶属度,而不仅仅只有两个可能的值,例如真和假。
关于模糊推理系统中的自适应和自动学习,自适应神经模糊推理系统(ANFIS)是解决非线性问题的最常见模型[3]。虽然ANFIS在处理非线性和复杂控制问题方面具有很高的泛化性,但由于其复杂的结构和梯度学习过程,计算成本相对较高。此外,它不够灵活且不易于调整,无法支持产品设计过程。而Mamdani模糊推理系统的隶属函数和规则可以相对容易地进行手动调整和修改,以适应不同的应用场景或设计要求。此外,人工智能的递归学习可以为Mamdani模糊推理系统提供一种自适应机制,以微调产品设计功能,从而适应不断变化的市场需求。
基于以上研究,本文结合大数据分析技术与多个人工智能技术(包括模糊关联规则挖掘、遗传算法以及递归学习),提出了一个多层人工智能产品设计方法,并对电动滑板车设计案例展开了具体研究分析。实验结果验证了本文所提方法的有效性和实用性。
全文HTML
-
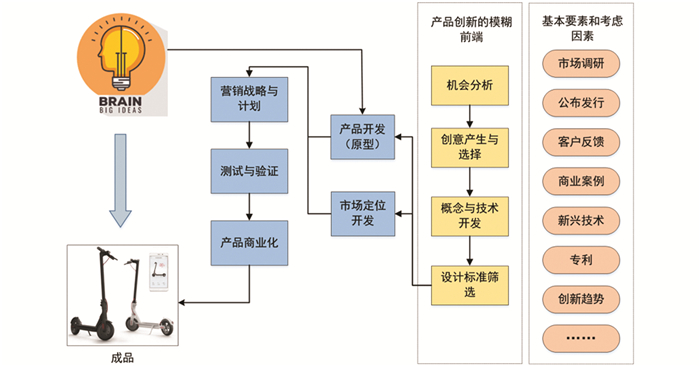
在工业产品设计开发的所有阶段中,FFE(即零阶段)是最复杂的,它涉及设计想法的范围界定、创意生成、创意评估,以及早期原型制作以进行迭代等过程。产品开发设计过程的FFE如图 1所示。
FFE阶段需要对信息技术、市场形势和客户视角等众多机会和障碍进行评估,其中要考虑来自多个维度的大量数据,特别是工业大数据。3V-3M特征应进一步应用于产品设计过程中的FFE阶段,以支持整个设计开发过程。表 1总结了工业大数据在产品设计的FFE阶段的特征。由表 1可知,在FFE阶段考虑的数据与工业大数据相匹配,因此探索相应的大数据分析对于整个产品设计中的决策过程至关重要。
FFE阶段的工业大数据分析可以更好地结合现有数据以确定产品设计的核心特征参数。一旦有了更多的数据,就可以有效地对方法进行微调,以递归的方式改进产品设计。通过考虑FFE数据,公司可以更好地将产品设计流程与客户需求相匹配,推出适宜的产品,实现价值最大化。
-
关联规则挖掘(ARM)作为数据挖掘领域的重要方法之一,被广泛应用于不同领域,如市场分析[4]、工业生产[5]、交通管理[6]、医疗信息管理[7]和社交分析[8]等。在产品设计领域,ARM通过分析客户的交易数据,能够有效地揭示产品之间的潜在关系,帮助设计团队更好地理解客户需求。
模糊关联规则挖掘(FARM)是基于模糊集理论对ARM方法的扩展,在挖掘关联规则中结合了模糊集和隶属函数。采用模糊理论,可以消除尖锐边界问题的影响。在许多现实生活数据集中,一种产品可能属于多个类别,传统方法无法考虑这些多类情况,传统ARM方法的模糊扩展可以弥补这一缺陷。模糊集理论的应用使得FARM能够更灵活地处理模糊性和不精确性,特别是在产品设计中,这对于涉及多个变量和复杂关系的情境尤为重要。文献[9]的研究成果表明,他们成功地将模糊Apriori算法与ARM结合,针对不确定性数据进行了改进,进而生成了一套高效的模糊关联规则。这为处理现实世界中存在的各种不确定性提供了新的思路和方法。近期的研究表明,FARM方法不断演进,一些学者将其与机器学习技术相结合,进一步提高了关联规则挖掘的精度和效率。文献[10]结合模糊关联规则挖掘和模糊C均值聚类算法,探索了在不同数据情境下的关联规则发现。文献[11]则在推荐系统中引入模糊关联规则,为用户提供更个性化的产品推荐。文献[12]的研究引入了模糊逻辑和鲸鱼优化算法,进一步提高了关联规则挖掘的效能。这种方法不仅在处理不确定性数据方面取得了显著成果,还为设计团队提供了更多在产品个性化和定制化方面的优化机会。
总体而言,FARM方法的不断发展为产品设计领域带来了更加先进和灵活的数据挖掘工具,为研究者和从业者提供了丰富的选择,以更好地理解和满足客户需求,推动了关联规则挖掘技术在现实环境的广泛应用。
1.1. 模糊前端(FFE)
1.2. 模糊关联挖掘(FARM)
-
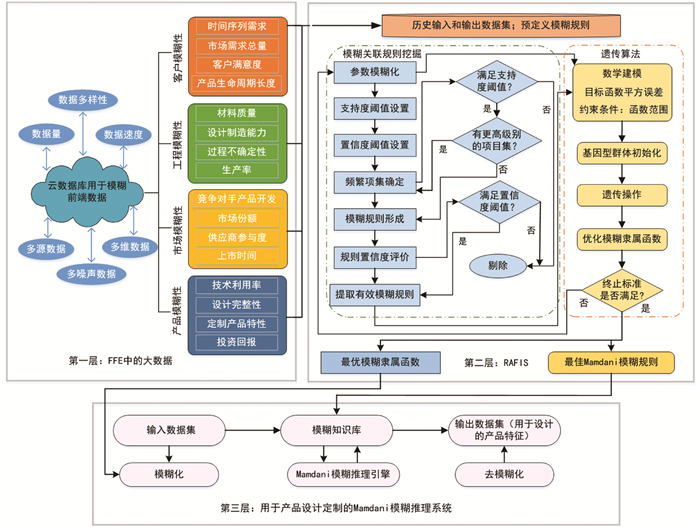
本文提出了一个多层人工智能产品设计方法,用于定制产品设计。该方法由FFE中的大数据、RAFIS、用于产品定制设计的Mamdani模糊推理系统3层组成,其构架如图 2所示。
-
该框架从FFE中大数据的结构表述入手,总结了客户模糊性、工程模糊性、市场模糊性和产品模糊性4个方面。FFE阶段的有用数据和信息必须从大量数据库中提取。由于在做产品设计特征决策时,涉及高度不确定性,为了发挥大数据分析的威力,因此需要将这4个方面的模糊性量化为一组可测量的值。
在客户模糊性方面,要总结客户反应和行为的不确定性,包括同类产品的时间序列需求、市场需求总量、客户满意度和产品生命周期长度。对于工程模糊性,生产过程的不确定性可能会影响产品开发的成功,需要考虑材料质量、设计制造能力、过程不确定性和生产率。市场模糊性方面,在瞬息万变的商业环境中成功进行产品设计具有一定的挑战性,因此需要考虑的因素包括竞争对手的产品开发、市场份额、供应商参与度和上市时间。对于产品模糊性,产品开发成功与否的不确定因素包括技术利用率、设计完整性、定制产品特性和投资回报。通过量化FFE阶段的模糊性,可以通过智能和数据驱动的方法进一步分析产品开发过程中的不确定性,从而为产品设计提供支持。鉴于大数据环境下需要处理大量数据,通过3V-3M原则对收集到的数据进行评估,从而建立工业智能。
数据处理包括提取、转换和加载,以便有效地组织数据以进入结构化评估过程。在现实生活中,Spark和Hadoop等大数据处理引擎的开发为处理大数据提供了高可扩展性。尽管硬盘可以存储大量数据,但可能没有可用的计算内存来分析数据,因此采用大数据处理引擎来确保数据预处理,以支持和提供决策。有了数据处理引擎,结构化数据就会存储在数据访问平台(如数据仓库和NoSQL储)中,供指定应用平台日后查询和检索。此外,最好利用基于云的基础设施进行大数据处理和访问,以充分利用大数据处理引擎的功能,并实现计算资源的动态分配。
-
为了优化Mamdani模糊推理系统的设置和系统参数,本文设计了一种新的智能方法,通过整合FARM和GA获得Mamdani模糊逻辑推理的合适设置,简称为RAFIS。FARM整合模糊集理论和数据挖掘技术,以提取前因后果之间的有用关系,并通过解决模糊隶属函数的优化问题,迭代改进模糊化。在开始使用RAFIS之前,产品工程师会提取历史输入和输出数据集,这些数据集分别与FFE特性和产品设计特征相关。此外,将根据业务逻辑组织预定义的模糊规则作为整个系统机制的先决条件。本文所提系统的步骤过程如下:
步骤1:根据历史输入和输出数据集均匀分配基长hkx,hkx表示第k个参数的第x个模糊隶属函数的基长,下标变量k=1,2,…,K(k为模糊系统参数编号,K为总参数量),x=1,2,…,X(x为模糊隶属度函数编号,X为每个参数的隶属函数数量),模糊系统范围变量rkt(t=1,2,…,T,T为数据集的样本总数),以及初始化的三角隶属函数Fkx。
步骤2:为规则挖掘过程定义支持度Snk和置信度On的阈值,n=1,2,…,N(n是规则的编号,N为规则总数)。
步骤3:使用预定义的模糊类别Fkx,Ckt可将显示FFE特性与产品设计特征之间关系的第t个样本对应于第k个参数的清晰值转换为模糊集,以便根据历史输入和输出数据集的每一行将每个参数表示为
其中:μFkx(Ckt)表示参数Ckt在模糊类别Fkx下的隶属度值。
步骤4:用Skx表示Ckt下不同数据行中的支持计数值之和,即Skx=
$ \sum\limits_{t \in T} {{\mu _{{F_{kx}}}}} \left( {{C_{kt}}} \right)$ ,若Skx的计算值满足Skx≥Snk则称Snkq为Skx的q-项集且令Snkq=Skx(q=1,2,…,Q)。步骤5:生成更高级别的可行项集,直到考虑输入输出参数可能组合的(Q-1)-项集(Q表示输入与输出参数的总数量),并重复上述步骤4以计算[Snk1,Snk2,…,Snk(Q-1)]的支持计数值。
步骤6:计算从2-项集到(Q-1)-项集的置信度值:
其中:
筛选出不满足置信度阈值On的规则。
步骤7:获取模糊关联规则列表,将其与预定义的模糊规则组合成模糊规则集R,作为模糊隶属函数优化问题的前提条件。
步骤8:优化三角隶属函数的基长
须满足
公式(4)为优化问题的目标函数,旨在最小化实际输出与估计输出之间的误差,其中jl为实际输出值;
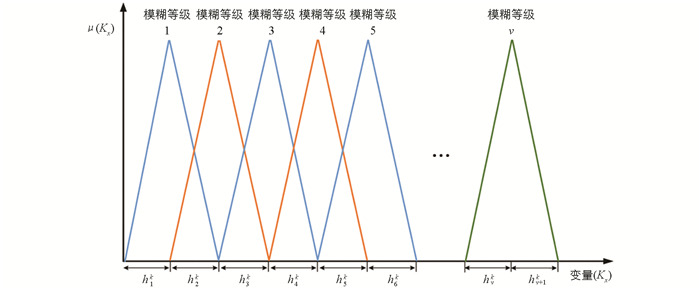
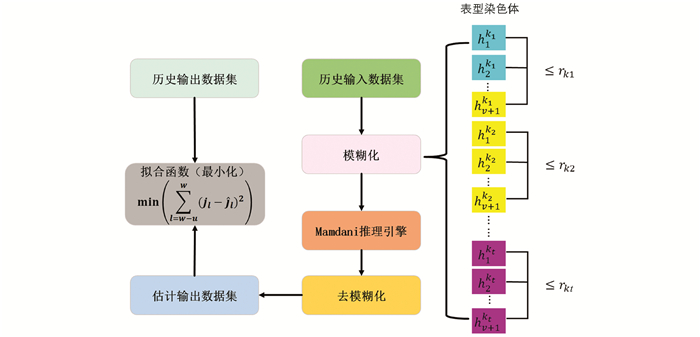
$ {{\mathop j\limits^ \wedge} _l}$ 为通过Mamdani模糊推理系统计算出的预测输出值;l为滑动窗起始点;u为滑动窗口大小即从终点w向前回溯u步的区间长度。公式(5)和(6)显示了对输入和输出基长的约束,其中符号hvip表示模糊系统输入参数ip(第p个模糊隶属度函数的输入参数i)在第v个模糊类别Fkx中的基长,如图 3所示。公式(7)显示了输入、输出和基长的非负约束。步骤9:为种群初始化建立表型染色体,其中基长是优化问题中的因变量。染色体或种群的个体代表如图 4所示。存储在双向量中的基长使用遗传算法进行优化。
步骤10:进行遗传操作以在染色体之间搜索接近最优的解决方案,包括选择、交叉和突变。随后,得到三角隶属函数的最优设置。
步骤11:如果满足终止标准,例如模糊推理引擎的误差和迭代次数,则获得最优的Mamdani模糊推理系统。否则,重复步骤3-9。
步骤12:将模糊隶属函数和模糊规则的最佳设置存储在知识库中,以便进一步构建Mamdani模糊逻辑。
-
在RAFIS中进行操作后,获得模糊隶属函数和模糊IF-THEN规则(即前因→结果)方面的最优设置,以制定合适的Mamdani模糊逻辑作为智能决策支持系统,以促进产品设计定制。在Mamdani模糊推理系统中,有模糊化、Mamdani模糊推理引擎和去模糊化等方法来提供模糊决策支持功能。
-
尽管进行调查和研究不能百分之百确保成功,但它们是了解客户需求和行为的关键策略。没有人能够完全准确地预测新产品的成功与否,但通过采用RAFIS可以为FFE阶段生成可供参考的结果。通过将客户需求与产品特征相关联,可以将丰富的客户信息直接输入到模糊知识库中以支持模糊化。然后,通过使用范围[0, 1]内的最优模糊隶属函数来推断模糊集和规则,将FFE数据(作为清晰的变量)从数字转换为隶属度。
-
推理引擎被视为执行一系列推理过程的核心元素,包括规则块形成、规则组合、规则触发、暗示和聚合等过程。利用RAFIS生成最优数量的模糊IF-THEN规则,并以系统的方式对这些规则进行组合和触发。输入新的输入数据集时,会考虑规则的IF部分,以评估隶属函数中的组合归属度,如公式(8)所示,其中μn表示为第n条规则的综合触发强度。隐含操作是在所有权重中选择最小隶属函数值作为第n条规则的综合权重。之后,使用一组综合权重和THEN规则,可以对输出隶属函数中的区域进行聚合。
-
去模糊化是从推理引擎中的集合区域确定清晰值的过程。从FFE数据中得出的模糊集被模糊化为与产品设计特征相关的可测量值。关于最近的模糊决策支持系统,有多种去模糊化方法可用于评估输出隶属函数中的聚合区域,包括总和中心(CoS)、重心中心(CoG)、面积中心(CoA)和加权平均法。可根据行业规范选择适当的去模糊化方法,将模糊集转换回清晰值。
2.1. 第一层:FFE中的大数据
2.2. 第二层:基于递归关联规则的模糊推理系统(RAFIS)
2.3. 第三层:用于产品设计定制的Mamdani模糊推理系统
2.3.1. 模糊化
2.3.2. Mamdani模糊推理引擎
2.3.3. 去模糊化
-
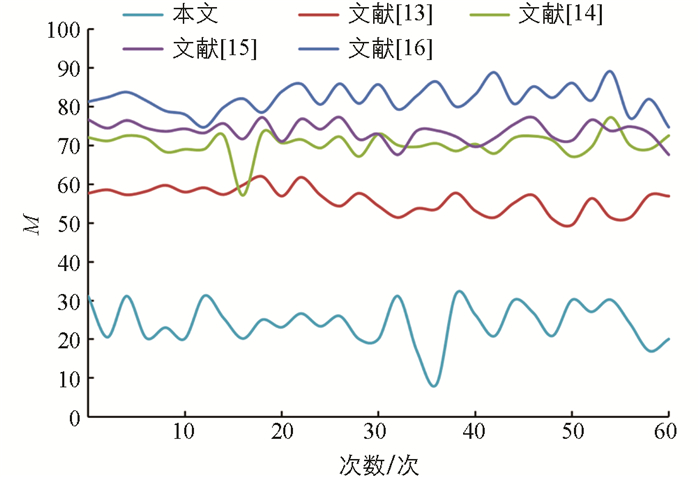
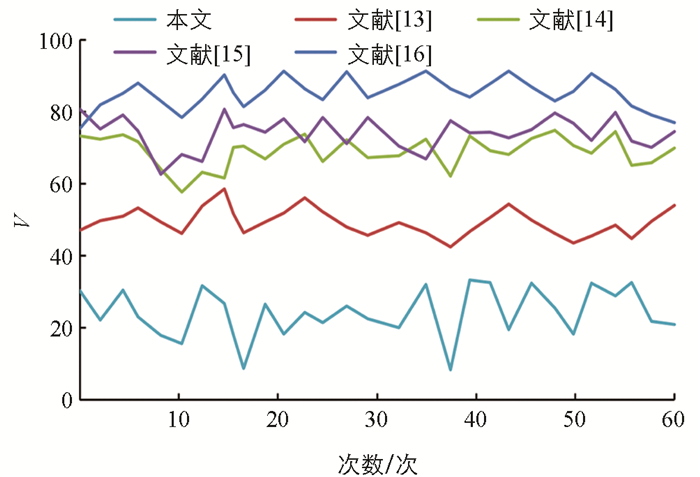
为了评估所提方法的有效性,将本文模型与文献[13-16]模型的建模结果进行了比较分析。在[0, 1] 区间选择了多个值进行实验和测试,并选择了建模误差最小的参数值。文献[13-16]模型的参数值分别设为0.1,0.99,0.95,0.9。为了在建模精度和计算时间之间取得折中,本文模型采用了不同的迭代次数和种群规模设置,将迭代次数设为200次,种群规模设为40个,突变和交叉概率分别设置为0.3和0.7。安排了60次验证测试。在每次测试过程中,从所有数据集中随机抽取两组数据作为测试数据,另外8组数据作为生成顾客需求模型的训练数据。
-
利用公式(9)和(10)中的平均绝对百分比误差M(MAPE)和误差方差V(VoE)来系统地比较和分析本文模型与其他4种模型的建模结果。
式中:jx表示为实际值;
$ {{\mathop j\limits^ \wedge} _x}$ 表示为预测值;T为总样本数。表 2列出了5种方法在60次验证测试中的MAPE和VoE平均值。
综上可知,本文方法的MAPE和VoE平均值均优于其他方法。
-
为了说明所提方法的可行性,本文以电动滑板车设计为经验案例展开研究。首先,以问卷调查的形式获取用户需求,了解产品特征点,收集电动滑板车在各电商平台上的销售情况及相关反馈评估,进行初步整合;然后,成立焦点小组,讨论产品设计指标和具体设计细节的可行性,并根据本文提出的多层智能结构设计电动滑板车模型。
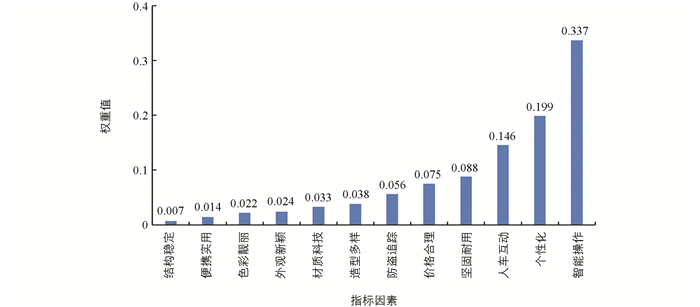
基本特性包括便携实用、结构稳定、坚固耐用等;扩展功能包括人机交互、防盗跟踪和智能操作;外观特性包括外观新颖、色彩靓丽、造型多样等;其他属性包括价格、材质、工艺等12个指标因素。各指标权重均采用FAHP方法计算,其中“智能操作”(0.337)、“个性化”(0.199)、“人车互动”(0.146)、“坚固耐用”(0.088)得分较高,是设计中首先需要满足的重要指标因素。在电动滑板车的后续设计过程中,在保证产品质量的基础上,简化了操作界面,配置了移动终端控制APP,形成了自身特点。其中,基本功能“结构稳定”和“便携实用”得分低的原因是电动滑板车的安全性是默认属性,作为交通工具,必须严格遵守国家标准和通用技术规范。各指标综合权重值的排名结果如图 7所示。
基于上述分析,研究人员对电动滑板车进行了创新设计,并生成了两种电动滑板车设计方案。
为了验证研究方法的有效性,采用模糊综合评价法对设计方案进行评价。评价指标集G=g1,g2,g3,…,gt,t=6,指标权重W由专家打分法得到,W=0.2,0.1,0.2,0.2,0.2,0.1。评价指标及相关说明见表 2。令电动滑板车设计方案的评价结果q1为满意,q2为一般,q3为不满意,分别将它们赋值为1,0.5,0,形成定量评价集,即q1=1,q2=0.5,q3=0。
设计该产品的满意度问卷。共有80人参与问卷调查,其中包括25名设计专业学生,15名教师和40名普通消费者。综合考虑该产品受众和购买力等因素,参与者年龄限制在20~50岁,共收集有效问卷76份。问卷调查分析结果详见表 4。
整合问卷数据,构建设计方案1的模糊评价矩阵R1:
计算设计方案1的评价向量H1,即:
结合定量评价向量Q和评价向量H1可以得到最终的综合满意度K1:
根据上述方法同理计算出设计方案2的综合满意度K2为0.801。
从设计方案满意度的评价结果来看,两个设计方案都取得了较高的评价满意度。设计方案1的综合满意度(83.3%)高于设计方案2(80.1%),其在“智能操作”方面得分优势明显。案例分析结果表明,基于本文所提方法的工业产品设计具有较高的客户满意度,验证了方法的可行性和实用性。
3.1. 实验设置
3.2. 有效性分析
3.3. 应用案例分析
-
为了避免产品设计中的常见缺陷,FFE阶段需要综合考虑大量信息,如客户数据、制造能力和市场趋势等。为此,本文提出了一种通用方法,即多层人工智能产品设计方法,用于支持产品设计中FFE阶段的决策过程。该方法集成模糊关联规则挖掘和遗传算法两个关键组成部分,构建了基于递归关联规则的模糊推理系统(RAFIS),用于识别模糊规则和优化隶属函数。然后,根据指定的输入参数,进行了Mamdani模糊推理引擎的优化设计,为产品设计过程提供充分的推理支持。所提出的设计方法在电动滑板车设计案例研究中得到了验证。通过本文研究,制造企业可以更好地了解市场需求,把握产品设计的方向,提高产品的创新性和竞争力。本文也为工业制造的智能化和可持续发展提供了有力的支持。本文仅限于特定行业,并且所使用的数据集有限。未来的研究工作将继续探索在考虑工业大数据的情况下,将所提出的方法应用于其他制造业和服务业。此外,由于RAFIS设计的灵活性,可以考虑使用其他优化算法,例如粒子群优化、模式搜索和模拟退火算法,以实现Mamdani模糊推理系统中的自动规则学习和参数调整。



 下载:
下载: