-
开放科学(资源服务)标识码(OSID):

-
近年来,声学黑洞结构(Acoustic Black Hole,ABH)作为一种新型轻质高效的被动减振降噪技术,受到人们越来越多的关注[1-4]。特别是在限制重量和空间的工程应用场合,如航空航天、电子电器、汽车工程等相关领域,使用声学黑洞结构可以在不增加总体结构重量的前提下,吸收和耗散大量的振动能量,达到降低振动和噪声的目的。在工程结构中适当嵌入声学黑洞,可以最小限度减少对结构力学性能和疲劳性能的影响,这种被动减振降噪技术相比传统被动控制和主动控制方式,具有结构简单、易于实现、减振性能优异等优点。因此,开展声学黑洞减振降噪结构的研究具有非常重要的现实意义。
声学黑洞类似于天体物理中黑洞的概念。Mironov[5]首先发现,当楔形薄板结构的厚度形式按照一定的幂函数降低时(幂指数不小于2),波传播的速度会随着板厚变小而逐渐降低,在理想的零厚度情况下波速会降低至零,从而实现波的零反射,这种结构被称为声学黑洞结构。然而,声学黑洞结构在上世纪80年代提出时,并未受到研究者的及时关注。直至本世纪初Krylov引入声学黑洞的概念后,学者们才开始逐渐深入研究声学黑洞结构的内在机理和特性,并开展了初步实验进行验证。目前,国内外学者们使用几何解析法、半解析法、近似解析法、传递矩阵法、有限元法等对声学黑洞梁结构进行了一系列研究。Krylov等[6-10]运用几何声学法分析了一维声学黑洞梁结构中弯曲波的传播过程,并将声学黑洞结构应用于板结构中,研究了截断厚度、阻尼材料等参数对反射系数的影响;Tang等[11-12]、Hou等[13]和Cheng等[14]基于拉格朗日变分原理建立了声学黑洞结构的半解析模型,采用Mexican Hat小波函数来表示声学黑洞边缘急剧变化的结构厚度,得到了阻尼层特性对一维声学黑洞结构动态响应的影响规律;Deng等[15]基于高斯函数建立了一维声学黑洞梁的动力学模型;Ma等[16]运用Daubechies小波函数建立了二维声学黑洞板的半解析模型;Wang等[17]基于Rayleigh-Ritz法建立了声学黑洞梁的动力学方程,分析了梁结构中能量的传递情况;曾鹏云等[18]通过半解析方法分析了带有声学黑洞特征的一维圆柱梁系统的动力学响应;O'Boy等[19-20]利用近似解析方法,分析了含有二维矩形声学黑洞形式矩形板和含有二维圆形声学黑洞形式圆板的频率响应特征;Georgiev等[21]基于Euler-Bernoulli梁理论,建立结构传递矩阵,进而利用阻抗矩阵变换,得到了弯曲波的反射系数;黄薇等[22]运用ABAQUS有限元分析软件建立了二维声学黑洞板结构模型,利用几何方法研究了弯曲波在声学黑洞区域的传播过程,最后通过激光超声实验系统进行成像与验证。
目前针对声学黑洞结构的研究还不够丰富和完善,数值方法在处理声学黑洞结构急剧变化的厚度时,网格离散化困难,求解模型巨大,求解得到的高频结果较差,难以快速进行结构参数化分析和结构优化研究。由于实际工程中结构几乎不存在理想边界条件,常常需要考虑各类弹性支撑条件[23-24]。有鉴于此,本文使用半解析Rayleigh-Ritz方法,建立任意边界条件下声学黑洞梁结构的振动分析模型。在此基础上,开展模态分析和动态响应分析,研究声学黑洞梁结构模态损耗因子和振动能量的变化情况,揭示声学黑洞区域内能量聚集与耗散的规律,以期为相关工程结构被动减振设计提供借鉴和参考。
全文HTML
-
针对声学黑洞梁结构的横向振动特性进行建模分析,所考虑的结构为细长梁,即梁结构长度方向尺寸远大于截面(厚度和宽度)方向尺寸,故建模时采用Euler-Bernoulli梁理论。
-
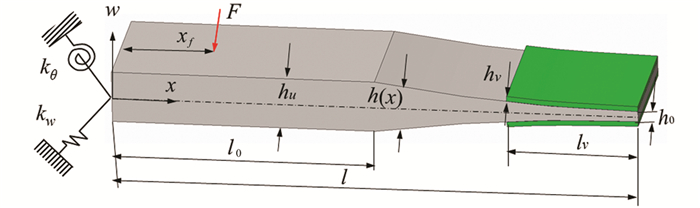
任意边界条件下声学黑洞梁结构振动模型如图 1所示。声学黑洞梁的长度为l,杨氏模量为E,惯性矩为I,密度和阻尼损耗因子分别为ρ和η。假设沿长度方向坐标为x,横向振动位移可以使用w(x)表示。为模拟任意弹性边界条件,梁左端使用1组线性弹簧表示线约束,1个旋转弹簧表示角约束,对应的弹簧刚度分别为kw和kθ。这样,自由或固支边界条件就可以通过将弹簧刚度系数取零或无穷大进行模拟,弹性约束边界条件则可以使用有限数值的刚度系数进行模拟。声学黑洞梁结构由均匀部分和变厚度部分组成,均匀部分长度为l0,阻尼层覆盖在其变厚度部分上,长度和厚度分别为lv和hv。阻尼层的杨氏模量、惯性矩、密度和阻尼损耗因子分别为Edamp、Idamp、ρdamp和ηdamp。声学黑洞梁和阻尼层的横截面积分别为S和Sdamp。声学黑洞梁受到的外界激励作用力F作用在xf处。
在声学黑洞梁结构厚度非均匀区域,结构厚度以幂函数形式变化,声学黑洞梁结构在整个长度范围内的厚度函数为分段函数,即:
式中:hu为梁结构的均匀部分厚度;h0为梁结构声学黑洞部分的截断厚度;p为指数常数,且不小于2。
-
在传统的自由、简支或者固支等约束条件下,梁结构的位移响应函数可以假设为傅里叶正弦或余弦级数形式,这将大大简化计算。然而在梁结构的两端位置处,即x=0和x=l处,对振动位移函数求导后,会出现导数始终为零的现象。那么,单独使用傅里叶正弦或余弦级数形式就无法表示梁结构两端转角的约束边界条件情况。为了解决位移响应函数在边界处导数为零的情况,本文在梁结构的振动位移函数中增加了附加项,以克服边界不连续现象。振动位移函数可以表示为改进傅里叶级数形式,即:
式中:ζ1(x)与ζ2(x)为振动位移辅助函数;Am、a、b为未知系数。
振动位移辅助函数的构造可以选用多种形式,为了简化计算过程,本文选取的辅助函数形式如下:
将式(3)代入式(2)中,可以得到完整的振动位移函数。通过振动位移函数对x连续求导,可得到位移函数的各阶导数,不难看出式(2)在梁结构两端处的导数存在且连续。
-
采用改进傅里叶级数构造位移函数后,可以得到相应能量项,进而使用Rayleigh-Ritz能量法求解。本文利用Hamilton原理获得振动位移函数中各项的未知系数,最终得到声学黑洞梁结构振动求解的统一表达式。
梁结构存在外部作用力时,系统的拉格朗日量可表示为:
式中:V为声学黑洞梁结构的总势能;T为声学黑洞梁结构的总动能;Wf为外力做功。任意边界条件下声学黑洞梁的横向振动总势能V包括结构应变能Vbeam和边界弹簧势能Vspring。阻尼层的应变能和动能分别为Vdamp和Tdamp。
声学黑洞梁结构以应变和应力形式储存的应变能表达式为:
模拟端部弹性边界的弹簧储存势能表达式为:
声学黑洞梁结构的总动能表达为:
声学黑洞区域贴敷的阻尼层储存的应变能表达式为:
阻尼层的动能表达式为:
外力做功的表达式为:
利用Rayleigh-Ritz能量法及Halmton作用原理,分别对振动位移函数中的未知系数取极值,即:
得到一系列关于未知系数的方程组后,将上述方程组进一步整理成矩阵形式,即:
式中:ω为角频率;K、M、Fmat分别为刚度矩阵、质量矩阵和外力矩阵。系数矩阵A可表示为:
求解式(13),即可得到声学黑洞梁结构在不同频率下的振动位移。当外力为零时,可以得到声学黑洞梁结构的固有频率和模态振型。
1.1. 声学黑洞梁模型
1.2. 位移场的改进傅里叶级数表达式
1.3. Rayleigh-Ritz法求解
-
本文选取的声学黑洞梁结构总长度l=1.0 m,宽度b=0.05 m,均匀部分厚度hu=0.01 m,截断厚度h0=0.001 m,均匀部分长度l0=0.5 m,指数常数p=2。声学黑洞梁所用材料密度ρ=7 850 kg/m3,杨氏模量E=2.06×1011 Pa,阻尼损耗因子η=0.005;阻尼层材料密度ρdamp=950 kg/m3,杨氏模量Edamp=5×109 Pa,阻尼损耗因子ηdamp=0.5。该声学黑洞梁沿长度方向的厚度函数为:
-
首先计算无阻尼层声学黑洞梁结构的自由振动特性,并与有限元法的计算结果进行比较。本文使用COMSOL软件建立声学黑洞梁的有限元模型,网格最大单元尺寸不超过0.005 m,满足分析频率要求。为保证COMSOL有限元分析结果的可靠性,需要进行网格尺寸测试,对模型网格进一步加密。若加密后的模型最大模态频率和加密前相差小于1%,即可认为网格尺寸已经收敛,可以得到准确的分析结果。不同网格单元尺寸下声学黑洞梁的模态频率结果如表 1所示。从表 1中可以看出,当单元尺寸为0.001 m时,COMSOL解已经基本收敛,可以用于计算结果的比较。
表 2给出了本文方法和有限元法计算得到的悬臂声学黑洞梁结构的前8阶模态频率,其中均匀端(x=0处)为固支状态,声学黑洞结构端(x=l处)为自由状态。傅里叶级数截断项数N取50、模拟边界的约束弹簧刚度取1×1012时,得到表 2中本文方法的计算结果。由表 2可知,本文方法和有限元法计算结果基本吻合,可以准确求得声学黑洞梁结构的振动特性。在同一台计算机上运行时(处理器为Intel Core i7-7700HQ,内存为8 GB),COMSOL计算需要3 s,本文方法只需要0.48 s,计算效率大大提高。
图 2给出了本文方法和有限元法计算得到的无阻尼层声学黑洞梁结构前21阶模态频率结果。由图 2可知,本文方法和有限元法计算结果几乎一致,再次验证了本文方法的正确性。有限元法在处理声学黑洞结构时,需要根据声学黑洞边缘处最小尺寸进行网格划分,可能存在网格扭曲变形的情况,在参数化分析和结构优化分析时网格难以实现快速重新划分,严重影响求解精度和计算效率。相比之下,本文采用的半解析Rayleigh-Ritz能量法,属于一种无网格化方法,不依赖于传统的网格结构,计算效率和求解精度高,可以快速进行结构参数化分析和结构优化研究。
由于采用了改进傅里叶级数形式,本文需进一步对比分析不同傅里叶级数截断项数N对计算结果的影响。截断项数的大小影响本文方法的收敛速度,表 3列出了不同傅里叶级数截断项数下悬臂声学黑洞梁结构前8阶固有频率的变化情况。由表 3可知,随着截断项数的增加,声学黑洞梁固有频率的计算精度逐渐提高,当截断项数超过50时,前8阶固有频率完全收敛,可见本文采用的改进傅里叶级数形式具有较快的收敛速度。
为进一步验证本文方法所建模型的有效性,通过实验对声学黑洞梁结构进行了模态测试,如图 3所示。模态实验所采用的声学黑洞梁结构长宽尺寸为0.2 m×0.01 m,厚度情况与前文一致。采用力锤法测试声学黑洞梁试件的加速度响应,锤击时使用B&K 3050型数据采集仪采集力锤和加速度计信号,通过计算机中的PULSE Labshop软件进行处理。
实验得到的前6阶模态频率与本文方法的对比情况如表 4所示。从表 4中可以看出实验测量结果与本文方法计算结果吻合良好,特别是前4阶模态频率的相对误差不超过2%,从实验角度验证了本文方法的有效性和准确性。两者误差来源主要包括传感器附加质量效应影响,以及力锤敲击力大小、方向和位置受人为因素影响等。
-
声学黑洞梁结构会出现声学黑洞效应,即变厚度声学黑洞部分会表现出对能量强烈的聚集作用。以无阻尼层声学黑洞梁结构为例进行分析,为了便于比较,使用均匀梁作为参考,除厚度部分外,均匀梁的其他参数与声学黑洞梁完全相同。相比梁结构,阻尼层的弹性模量和密度非常小,对模态频率的影响可以忽略。无阻尼层均匀梁和声学黑洞梁固有频率的变化情况如表 5所示。从表 5中可以看出,除了第1阶外,在相同模态阶次下,声学黑洞梁相比均匀梁,其固有频率大大降低。
图 4给出了无阻尼层情况下,均匀梁和声学黑洞梁(图中ABH梁)的前21阶固有频率变化情况。由图 4可以看出,在相同频率范围内(如2 000 Hz内),声学黑洞梁相比均匀梁的模态阶次更多,意味着固有频率越来越密集。
图 5和图 6给出了无阻尼层均匀梁和声学黑洞梁前6阶模态振型的变化趋势。由图 5和图 6可以看出,均匀梁的模态振型为梁结构的整体变形,而声学黑洞梁结构的模态振型主要集中在声学黑洞部分,意味着外界输入的振动能量会向声学黑洞区域聚集。
-
图 7给出了悬臂边界条件下无阻尼层均匀梁、有阻尼层均匀梁、无阻尼层声学黑洞梁和有阻尼层声学黑洞梁结构的模态损耗因子的变化情况。由图 7可以看出,无阻尼层均匀梁和无阻尼层声学黑洞梁在各个模态频率处的阻尼损耗因子与结构材料相同,增加阻尼层后,均匀梁和声学黑洞的阻尼损耗因子大大增加。除了第1阶模态频率处,声学黑洞梁相比均匀梁,在其他模态频率处的阻尼损耗因子均增大近5倍,这表明声学黑洞结构聚集的能量可以通过阻尼层迅速耗散。由于第1阶模态频率大小和振型形式基本一致,故声学黑洞梁相比均匀梁在此处的模态损耗因子变化并不明显。
-
图 8和图 9分别给出了悬臂边界条件下,在0.1 m处施加1 N的激励力时,有阻尼层均匀梁和有阻尼层声学黑洞梁均方根振速的变化情况。结构振速代表结构振动的强烈程度,可以用于表征振动能量的大小。由图 8可以看出,有阻尼层均匀梁结构在外界激励作用下表现出了整体剧烈振动,振动能量传递到各个位置处,以振速表征的振动能量为27 dB,间隔分布在不同位置,未表现出局部聚集现象。相比之下,由图 9可以看出,有阻尼层声学黑洞梁结构在外界激励作用下主要表现为声学黑洞区域的局部振动,声学黑洞区域的振动能量远远超过其他区域(x≥0.5 m),特别是低频段在声学黑洞梁结构的边界端面处,以振速表征的振动能量超过120 dB,表现出局部聚集现象。声学黑洞区域内聚集的能量可以被贴敷的阻尼层材料进行有效地吸收耗散。
2.1. 准确性和收敛性验证分析
2.2. 均匀梁和声学黑洞梁模态振型比较
2.3. 均匀梁和声学黑洞梁模态损耗因子比较
2.4. 均匀梁和声学黑洞梁振动响应比较
-
本文基于Euler-Bernoulli梁理论,利用改进傅里叶级数形式和半解析能量方法建立了任意边界条件下声学黑洞梁结构振动特性分析的统一模型,研究了任意弹性边界下声学黑洞梁结构的自由振动和强迫振动特性,得到以下结论:
1) 基于改进傅里叶级数形式构建声学黑洞梁结构的振动位移函数,利用Rayleigh-Ritz能量法建立声学黑洞梁结构的振动求解模型,具有较高的准确性和较好的收敛性。
2) 除了第1阶模态频率外,在相同模态阶次下,声学黑洞梁相比均匀梁,其固有频率大大降低,模态频率更加密集,模态振型集中在声学黑洞区域,同时模态阻尼损耗因子增大近5倍,表现出对振动能量强烈的聚集和耗散作用。
3) 在外界激励作用下,均匀梁振动能量会传递到结构各个位置处,以振速表征的振动能量为27 dB,而声学黑洞梁结构在声学黑洞区域的振动能量超过120 dB,远远超过其他区域,特别是在声学黑洞梁结构的边界端面处。
本文以模态损耗因子和均方根振速为表征研究了声学黑洞梁结构振动特性变化规律。后续可基于本文假设的改进傅里叶级数形式,利用Rayleigh-Ritz法建立声学黑洞板壳结构的振动分析模型,将本文方法进一步拓展至二维和三维结构。



 下载:
下载:







