-
开放科学(资源服务)标识码(OSID):

-
根据《中国统计年鉴2024》及公安部数据,中国机动车保有量达4.53亿辆,较2023年增长约16.2%,机动车驾驶员数量突破5.42亿人,新能源汽车保有量同比激增51.5%[1]。《2024年国民经济和社会发展统计公报》显示,2024年我国交通事故死亡人数为61 703人,其中行人死亡占比超过20%,而头部损伤是导致行人死亡的首要原因[2-5]。因此,面向我国复杂的人车混行交通场景,降低行人在事故中的损伤风险,尤其是降低行人头部损伤风险对提升我国道路交通安全具有重要意义。
当前L2级及以上辅助驾驶在乘用车新车渗透率已超过70%,我国典型城市道路交通在中长期将处于传统汽车、智能驾驶汽车与行人、两轮车等弱势交通使用者混行状态,车辆辅助驾驶系统面临更复杂的交通场景安全挑战,而现有车辆主动安全技术虽可降低事故发生概率,但还无法杜绝事故发生,尤其针对出行意图高度随机、缺乏有效防护装置的行人与车辆碰撞事故问题[6-7]。当前研究发现,汽车自动紧急制动系统(AEB)不仅可以在一定程度上缓解车辆与行人的交通冲突,还能在事故不可避免的高风险场景下有效降低行人头部撞击损伤风险[8-9]。文献[10]研究发现行人损伤模式与碰撞速度呈现显著相关性:在低速碰撞(≤30 km/h)情况下,行人与地面的二次碰撞往往造成比车辆直接撞击更为严重的伤害;而当碰撞速度提升至40 km/h及以上时,行人头部损伤则主要源于与车辆的首次接触冲击。文献[11]基于行人运动学响应和头部损伤特征,对比分析完全制动与控制制动策略下不同参数对行人头部一次/二次损伤的影响,验证了制动控制策略对降低行人头部损伤风险的积极作用。文献[12]提出了一种基于转向和制动结合的自适应模型预测控制避碰策略。文献[13]开发了集成制动与转向的紧急避碰系统,通过计算最小避碰距离并优化干预时机来降低碰撞风险。
当前国内外学者针对车辆单一制动、制动与转向协同优化降低事故风险方面进行深入研究,在制动、转向控制参数对行人损伤影响分析方面也开展了相关研究,但针对以行人损伤为目标的车辆控制策略优化问题还需进一步探索,主要表现在:一方面车辆制动过程对行人损伤影响机理尚不明确,另一方面行人损伤结果高度随机,与碰撞环境参数难以形成趋势明显的量化关系,导致车辆控制策略优化困难。
为此,本研究基于中国交通事故深度调查(CIDAS)数据库中的轿车—行人碰撞事故案例,构建基于多体动力学仿真软件MADYMO与优化设计平台ISIGHT的联合仿真环境,实现事故场景高效重建;引入带精英策略的非支配排序遗传算法(NSGA-Ⅱ)对重建模型进行参数优化,研究车辆控制制动策略对头部与车辆接触加速度峰值ACC1、头部与地面接触加速度峰值ACC2和HIC值的影响机制,揭示关键影响因子的变化规律及其相关性;结合自动化仿真与智能优化技术,提出以降低行人头部损伤为目标的车辆制动控制策略,以期为车辆主动安全系统制动曲线优化提供理论依据与工程实现路径,对提升复杂交通场景下行人保护性能具有重要参考价值。
全文HTML
-
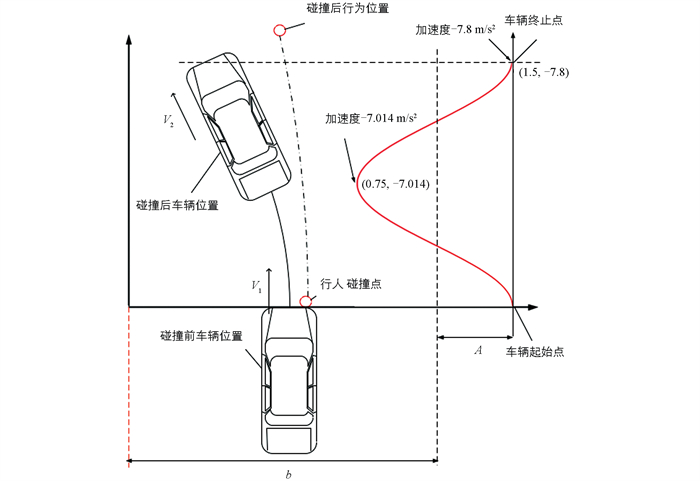
车辆在运行过程中遇到突发行人干扰,车辆采用通过优化的制动系统作为避险方式。假设车辆与行人碰撞前后位置如图 1所示,V1为碰撞时车辆速度,V2为碰撞后车辆速度。通常车辆在紧急制动过程中会采用完全制动方案,通过研究发现分阶段制动对降低行人头部损伤有较好收益。为了便于参数优化,本研究以余弦曲线为基础,通过更改其相位、周期和幅值实现制动曲线控制。车辆制动控制过程如图 1所示,控制制动曲线如图中红色曲线所示,计算公式如下所示:
式中:A为振幅大小;a为周期系数;t为初始相位;b为上下平移距离。
行人在碰撞过程中的头部损伤评价指标采用HIC值。HIC值通过计算头部在任意时间间隔(t1至t2)内平均加速度来量化损伤风险[14],其计算公式如下所示[15-16]:
式中:α(t)表示头部质心的合成加速度,单位为g,1 g=9.8 m/s2;t1-t2表示HIC取最大值时的时间间隔。本研究采取HIC36头部损伤准则,HIC取最大值时的时间间隔为36 ms。
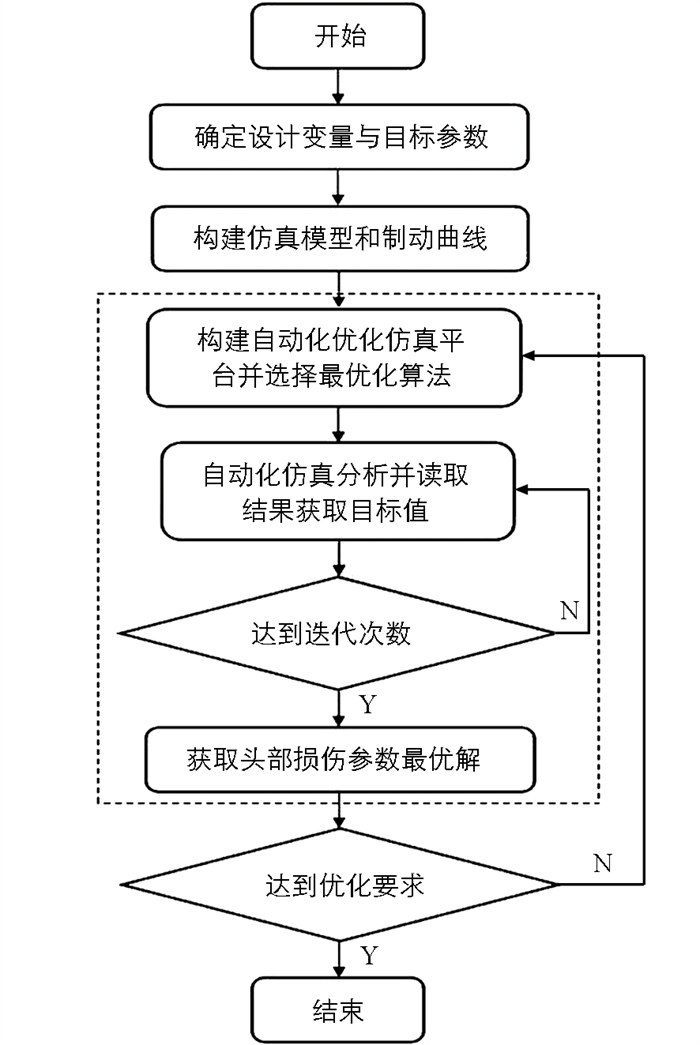
本研究基于ISIGHT 5.9构建优化框架,其中包括MADYMO主程序模块、输入与输出参数计算器模块以及优化算法模块[17],优化框架图如图 2所示。
首先,本研究以制动曲线控制参数为设计变量,以行人头部HIC值为优化目标,借助MADYMO软件对事故场景进行重建,构建碰撞场景仿真分析模型,将设计变量作为仿真分析的输入,将仿真计算HIC值作为优化目标。接着,利用ISIGHT构建自动优化仿真平台,调用MADYMO构建的事故重建模型进行自动计算,并读取优化结果和目标值,利用NSGA-Ⅱ算法分析结果和目标值并进行迭代优化,输出优化平台计算的头部损伤参数最小值和对应的制动曲线控制参数,即为最优结果。最后,将最优结果重新代入仿真模型进行计算,获得除优化目标外所有行人损伤值,以及行人在碰撞过程中的运动响应和三维动画。本研究的优化问题描述如下:
其中:F(X)为目标函数;fi(x)为N维目标集的第i个子目标函数;xj为M维设计变量的第j维列向量。
优化过程将多个子目标函数按照其权重系数与尺度参数进行线性加权组合,构建出用于指导迭代优化方向的总目标函数。给定一组子目标函数,其对应的权重系数为wn,缩放因子为sn,本研究的权重系数和缩放因子均设为1,最优化算法中Objective function值为输出变量的总和,该聚合函数可以在优化过程中动态调整各子目标的贡献,确保算法朝着全局最优解方向高效收敛。
-
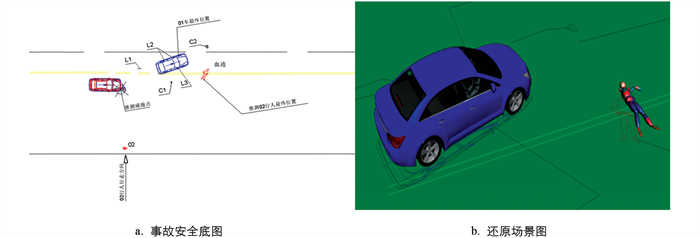
基于CIDAS数据库,以某轿车与行人碰撞事故为例进行模拟分析,案例特征如下:行人突然横穿道路,被车辆前部右侧撞击后死亡;事故车辆(雪佛兰CRUZE型轿车)主要损伤集中于前部发动机罩区域,具体表现为罩盖中部偏右位置呈现显著凹陷变形,车辆其余结构部件未明显形变;由于事故现场缺乏监控视频资料,无法直接通过影像数据验证所构建碰撞模型的有效性。为此,本研究采用事故现场底图作为基础数据,运用PC-Crash 12.0仿真软件平台进行事故场景重建,旨在精确获取涉事车辆的动力学参数及行人碰撞过程中的运动学特征。基于PC-Crash 12.0的仿真重建结果,提取人车碰撞动力学关键参数,并借助MADYMO构建精细化人车碰撞模型。最终,通过对比MADYMO仿真结果与PC-Crash重建场景的动力学响应,验证所建模型的可靠性与准确性。还原场景和事故案例底图如图 3所示。
鉴于事故案例中行人身高为174 cm,体重为75 kg,与MADYMO软件库中第50百分位男性假人模型(Hybrid Ⅲ 50th)具有高度相似性,为保持仿真精度并提高计算效率,本研究直接采用该标准假人模型进行碰撞仿真分析,未进行额外的模型缩放处理。
本研究中轿车主要外形参数如表 1所示,采用MADYMO对事故进行重建。本研究建立了高精度车辆三维模型,重点确保车头部位的几何特征与原事故车型保持高度一致。通过PC-Crash事故还原和MADYMO仿真的对比,验证重建模型的有效性,如表 2所示。
仿真结果表明:事故发生时,行人初始位于车辆右前方,车头右前侧首先与行人下肢发生碰撞接触。碰撞力导致行人上半身绕接触点旋转,头部与发动机罩中右部区域发生二次碰撞,造成头部损伤。随后行人被抛向前方,在空中完成360°旋转后,以下肢着地的方式与地面发生最终碰撞。事故车辆的损伤特征显示,发动机罩中右部出现明显凹陷变形,与仿真中行人头部碰撞位置完全吻合,且车身其他部位未见明显损伤,进一步验证了仿真结果的可靠性。
-
当车辆在同一事故中采用不同控制策略时,车辆与行人的相对运动轨迹发生变化,改变了行人与车辆的接触位置以及与车辆接触后的抛射轨迹,进而影响行人与车辆接触造成的损伤。而行人落地姿态存在不可预测性,可能引发头部与地面的剧烈二次碰撞,进一步加剧损伤风险。这种损伤机制的差异性突显了行人保护系统中空间定位因素的重要性。
课题组在前期研究[18]中对比分析了行人与车头左前方、正前方和右前方碰撞时,智能汽车集成自动紧急转向(AES)系统对行人头部损伤的影响,发现在车辆控制过程中增加合适的偏转角度可以显著降低行人头部受伤风险。因此本研究在现有研究基础上将碰撞时的车速设为40 km/h,车辆带有初始偏转角度,设计两种制动方案:方案1,车辆采用完全制动,制动减速度值恒为-7.8 m/s2;方案2,车辆采用预设余弦曲线作为控制制动曲线,余弦制动曲线如公式(5)所示。在此基础上开展仿真分析,并对仿真实验结果进行数据分析处理,获取Hybrid Ⅲ第50百分位男性假人模型在不同位置下的头部损伤HIC值以及ACC1、ACC2,如表 3所示。
根据车速为40 km/h时两种制动策略行人损伤数据对比仿真结果可知,当行人位于车头前方中间位置时,得到的HIC值、ACC1和ACC2结果普遍高于其他两种位置情况,制动策略对比发现控制制动策略的损伤结果低于完全制动策略,特别是HIC值大幅降低。当行人位于车头前方右侧时,损伤结果整体低于其他两种位置,主要由于行人未在车辆转向方向一侧,使得行人被撞倒后头部未与发动机罩发生直接正面接触,而是头部和车头右侧边轻微擦碰,虽然控制制动策略的ACC1略低于完全制动策略,但控制制动策略的ACC2更高。当行人位于车头前方左侧时,控制制动策略的ACC2和HIC值相对于完全制动策略有小幅度改善,但是ACC1基本上没有改变。
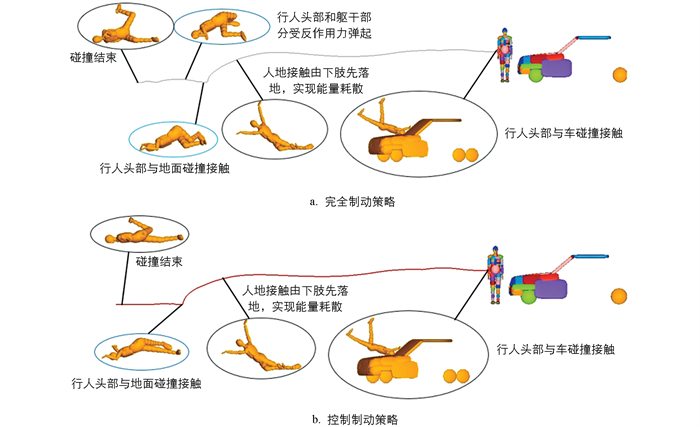
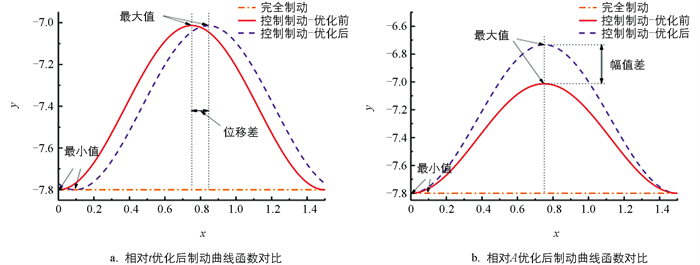
对比分析不同车辆制动策略对行人碰撞动力学的影响。在40 km/h车速下实施完全制动策略时,车辆横向加速度的改变使行人运动学响应产生显著变化。碰撞过程中行人呈现逆时针旋转(θ<270°),并通过下肢—上肢—头部的序列式撞击实现能量耗散。该模式虽将头部首次接触延迟至碰撞序列末端,但地面反作用力引发的二次抛掷运动仍会导致HIC值上升(图 4a)。采用控制制动策略后,系统通过实时调节制动力矩实现了碰撞能量梯级耗散。在此工况下,行人保持逆时针旋转(θ<270°)的同时,其碰撞后运动轨迹呈现渐进式地面接触特征,减少了对地面的冲击力且有效抑制了二次弹起现象,进一步降低对行人头部的损伤(图 4b)。在制动系统条件下,可有效调控行人与地面接触的时空序列,这种基于能量耗散路径优化的损伤缓释机制,为智能紧急制动系统的控制算法设计提供了理论依据。优化控制策略中采用的余弦函数制动曲线,因其渐进式力矩变化特性,在行人与车辆非正交碰撞中,针对中等车速范围(25~50 km/h)的交叉口左转车辆与行人冲突事故,该系统最为适用,其平滑的减速度梯度,能有效协调转向与制动的时空耦合效应,既可实现碰撞能量沿行人运动切向的最优耗散,又能抑制因车辆俯仰导致的二次碰撞风险。
控制制动策略对减轻车头前方右侧行人的损伤未达预期效果,但当行人在车头前方左侧和中间位置时,控制制动策略都能帮助行人降低头部损伤,特别是在行人位于中间时HIC值降低了26.36%,行人位于左侧时HIC值降低了24.12%。
-
本节从控制制动曲线的振动频率、振动幅度和相位出发,选取样本进行相关性分析。分析某一变量时,其余两个变量均保持预设的余弦函数曲线不变,研究曲线变化与行人头部损伤的关联。行人损伤数据如表 4-表 6所示。
如表 5不同振动幅度下的行人损伤仿真数据结果所示,无论行人位于车头前方何种位置,通过增大振动幅度对ACC1的影响几乎为零,结果都略好于完全制动的情况。当行人位于右侧时,HIC值都会处于较低的范围,并且与完全制动策略产生的HIC值相差很小,进一步证明当行人位于车辆前方右侧时,制动曲线对行人HIC的影响较小;当行人位于中间位置和左侧位置时,随着振动幅度减小,ACC2和HIC值相对于原制动曲线策略损伤结果会降低,尤其是当行人位于中间位置时,损伤结果的变化幅度整体较大,当a从0.786变成0.393后,减小振动幅度能够大幅降低中间位置行人的ACC2和HIC值,同时会导致在车头前方右侧位置行人的ACC2急剧增长,可能是由于车头转向后导致行人从车辆侧面滑落,头部先着地引起的。总而言之,随着振动幅度的增大,当行人位置位于中间和左侧时损伤结果呈现总体增大的趋势,行人位于右侧时,影响关联性很小。而不同振动频率下的行人损伤数据和不同相位下的行人损伤数据结果分别如表 4和表 6所示,表现出不确定性。因为相位移动分析在制动曲线优化中占据主导地位,其直接关联时间控制精度、动态响应匹配和多系统协同,同时更符合工程实践中的硬件限制与控制灵活性需求。本研究将从相位变化和振动幅度中选取相位变化进行最优值的求解,通过自动化仿真平台结合最优化算法目标分别以相位量变化和振动幅度为优化变量寻求控制制动曲线的最优解,并研究随优化变量变化的损伤结果趋势。
-
本研究基于NSGA-Ⅱ算法对选取变量进行联合自动化仿真分析HIC和3 ms累积头部质心加速度变化,优化过程中得到共计482组解集,共用时15 h,优化过程中各优化目标认定为同等重要,即具有相同权重,优化过程如图 5所示。
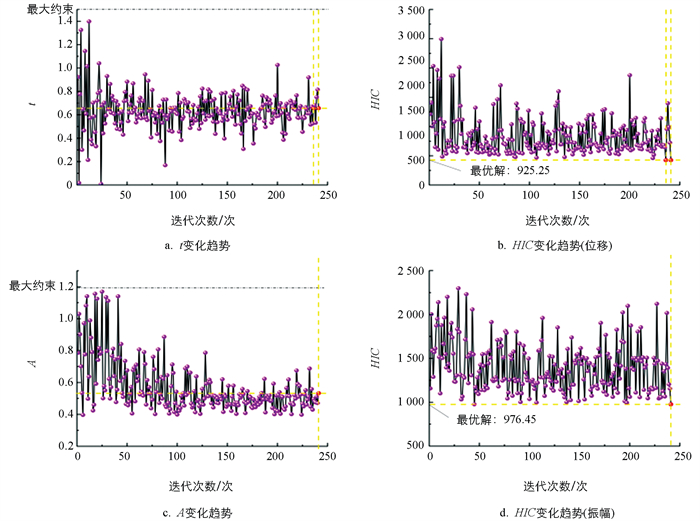
仿真结果表明,在相位变化作为优化变量的情况下,第236次和241次迭代获得了最优解,其中相位参数t=0.656 721 786 7时,HIC指标达到最优值925.25,同时3 ms累计头部质心加速度为1 184.6 m/s2,该组参数构成了最优解集。基于此优化结果推导出的控制制动曲线函数如公式(6)所示,其与基准曲线的对比分析如图 6a所示。当以振幅作为优化变量时,第45次和241次迭代产生了最优解,振幅参数A=0.533 511 860 3对应的HIC值为976.45,3 ms累计头部质心加速度为1 212.2 m/s2,该组参数同样构成了最优解集,其对应的优化制动曲线函数如公式(7)所示,相关曲线对比结果如图 6b所示。
对比分析显示,相位优化方案在HIC指标和头部加速度控制方面均优于振幅优化方案,这一结果验证了相位参数在制动曲线优化中的关键作用。
根据HIC值随相位t变化散点图,如图 7a所示,当t在0到0.57之间变化时,HIC值随相位变化降低,当t在0.57到1.5之间变化时,HIC值随相位变化增大,t在0.35到0.85之间收敛。图 7b所示,3 ms累积头部质心加速度变化趋势与HIC变化大致相同。如图 7c所示,遗传算法对振幅A的取点范围收敛集中在0.4到0.75之间,能够发现在这个范围内HIC值偏离散,振幅越小HIC值不一定会更小,但总体而言HIC随着A的增大而上升。3 ms累积头部质心加速度变化趋势与HIC变化大致相同,如图 7d所示。
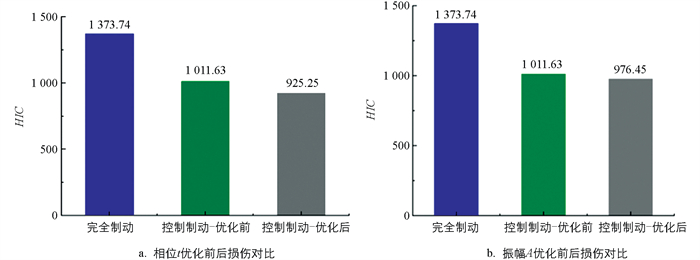
将完全制动曲线、控制制动曲线和优化后的控制制动曲线产生的HIC值进行交叉对比,如图 8所示。研究结果发现,车辆采用预设余弦曲线作为制动控制策略相较于车辆完全制动策略,行人头部HIC值降低26.36%;车辆采用经本研究构建的车辆紧急制动优化框架获得的制动策略,以相位t作为优化变量时行人头部HIC值比优化前的控制制动策略降低8.54%,相较于车辆完全制动时的头部HIC值降低了32.65%。以振幅A作为优化变量时行人头部HIC值比优化前的控制制动策略降低3.47%,相较于车辆完全制动时的头部HIC值降低了28.92%。研究结果说明了本研究构建的车辆紧急制动策略优化框架的有效性。
3.1. 制动策略分析
3.2. 控制制动曲线相关性分析
3.3. 最优化算法分析结果
-
本研究以降低行人头部损伤为目标,提出了结合ISIGHT和MADYMO仿真平台的车辆制动避撞策略的优化框架,并基于CIDAS数据库中某车型与行人碰撞案例,对比分析车辆完全制动、控制制动及通过构建的框架优化后的制动方案对案例中行人碰撞历程和头部损伤的影响关系,研究结果验证了本研究提出的车辆制动策略和优化框架的有效性。主要结论如下:
1) 通过对比真实案例中优化前控制制动策略对车头前方3种位置的行人造成的头部损伤发现,行人位于右侧,制动曲线策略对头部损伤HIC值影响并不明显,当行人位于左侧位置时,会略微改善行人的头部损伤结果,当行人位于中间位置时,能够从头部与车辆接触加速度峰值ACC1、头部与地面接触加速度峰值ACC2和HIC值3方面有效降低损伤结果,证明提出的余弦形式控制制动曲线在降低行人碰撞损伤方面的有效性。
2) 通过对比控制制动曲线的振动频率、振动幅度和相位变化对行人损伤的影响,研究结果表明,振幅A从0.393增大到0.786再增大到1.179时,HIC值从1 011.630上升至1 910.670再上升至2 045.200。当行人位于车头前方中间和左侧位置时随振动幅度的增大,ACC2和HIC值先增大,后在一定区间内保持稳定慢速增长,而相位的变化对行人损伤无明显趋势,而振动频率和相位变化对损伤结果存在不确定性。
3) 通过基于ISIGHT和MADYMO结合基于带精英策略的非支配排序遗传算法(NSGA-Ⅱ)的联合自动化仿真对相位变化以及振幅变化分析结果,当原函数相位变化t向左平移0.656 721 786 7时,优化后控制制动曲线产生的HIC值为925.25,相对于优化前控制制动策略降低的HIC值进一步降低了8.54%,较车辆完全制动时降低了32.65%,有效优化了行人头部损伤。HIC值随着振幅的增大,总体会存在升高趋势,但是并不绝对,例如根据以振幅为输入变量的最优仿真分析结果可知,当振幅A为0.533 511 860 3时,优化后控制制动曲线的HIC值最低,为976.45,行人头部HIC值比优化前的控制制动策略降低3.47%,相较于车辆完全制动时的头部HIC值降低了28.92%。
本研究探讨了车辆紧急制动策略对降低车辆与行人碰撞事故中行人损伤的潜力,为智能驾驶汽车紧急避险策略的设计和开发提供了理论和方法参考。



 下载:
下载: