-
差分方程(系统)作为微分方程及时滞微分方程的离散形式,在经济学、生态学、计算机、系统工程学等学科上有很多应用,取得了不少成果[1-9].模糊差分方程是差分方程的一种推广形式,系统中参数及初始值为模糊数,解为模糊数数列.最近有关模糊差分方程解的动力学行为研究已引起部分学者的关注,取得了一些有意义的成果[10-22],基于此,本文进一步讨论如下三阶非线性模糊差分方程
其中:A是正模糊数;初始值x-2,x-1,x0是正模糊数.
为方便起见,首先给出下列定义:
定义1 A为模糊数,如果A:
$\mathbb{R}$ →[0, 1]满足(ⅰ)-(ⅳ)(ⅰ)A是正规的,即存在
$x \in \mathbb{R}$ 使得A(x)=1;(ⅱ) A是模糊凸的,即对所有t∈[0, 1],
$ {x_1}, {x_2} \in \mathbb{R}$ 使得(ⅲ) A是上半连续的;
(ⅳ) A的支撑,
${\rm{supp}}A = \overline {\bigcup\nolimits_{\alpha \in \left( {0, 1} \right]} {{{\left[A \right]}_\alpha }} } = \overline {\left\{ {x:A\left( x \right) > 0} \right\}} $ 是紧的.A的α-截集表示为
${\left[A \right]_\alpha } = \left\{ {x \in \mathbb{R}:A\left( x \right) \ge \alpha } \right\}$ ,α∈[0, 1],显然[A]α是闭区间.如果${\rm{supp}}A \subset \left( {0, \infty } \right)$ ,则模糊数是正的.显然如果A是正实数,那么A是模糊数且[A]α=[A,A],α∈(0,1].即A是平凡的模糊数.定义2 设A,B是模糊数,[A]α=[Al,α,Ar,α],[B]α=[Bl,α,Br,α],α∈(0,1],模糊数空间的范数为:
距离为
根据文献[11, 13]给出模糊数数列有界和持久性定义如下:
定义3 如果存在一个正实数M(或N)使得
或
则称模糊数数列(xn)是持久的(或有界的).
如果存在正实数M,N>0使得
则称(xn)是有界和持久的.如果范数‖xn‖,n=1,2,…,是无界数列,则称(xn),n=1,2,…,是无界数列.
定义4 如果正模糊数数列(xn)满足方程(1),则称xn是方程(1)的正解.如果正模糊数x满足
则称正模糊数x是(1)式的正平衡点.
定义5 设正模糊数数列(xn),正模糊数x使得
及
如果limn→∞D(xn,x)=0,则n→∞时,模糊数数列(xn)关于D收敛于模糊数x.
定义6 (ⅰ)设方程(1)有正平衡点x,如果对任意ε>0,存在δ=δ(ε)>0,使得方程(1)的每一个正解xn,满足D(x-i,x)≤δ,i=0,1,2,有D(xn,x)≤ε,n>0,则称方程(1)的正平衡点x是稳定的.
(ⅱ)如果它是稳定的且当n→∞时,方程(1)的每一个正解关于D收敛于正平衡点x,则称方程(1)的正平衡点x是渐近稳定的.
全文HTML
-
首先研究方程(1)正解的存在性,需要下面的引理.
引理1[23] 设
$f:{\mathbb{R}^ + } \times {\mathbb{R}^ + } \times {\mathbb{R}^ + } \times {\mathbb{R}^ + } \to {\mathbb{R}^ + }$ 是连续的,A,B,C,D是模糊数.那么引理2[23] 设u∈E~(模糊数空间),[u]α=[u-(α),u+(α)],α∈(0,1].那么u-(α)与u+(α)可以看成(0,1]上的函数,满足
(ⅰ) u-(α)非减和左连续;
(ⅱ) u+(α)非增和左连续;
(ⅲ) u-(1)≤u+(1).
反之,对任意定义在(0,1]满足上面(ⅰ)-(ⅲ)的函数a(α)和b(α),存在u∈E~,使得对任意α∈(0,1],[u]α=[a(α),b(α)].
定理1 考虑方程(1),其中A是正模糊数.那么对任意正模糊数x-2,x-1,x0,(1)式存在唯一正解xn.
证 证明类似于命题2.1[14],略.
下面给出方程(1)模糊正解的性质,需要下面的引理.
引理3 对于差分系统
其中p,q及初始值y-i,z-i,i=0,1,2是正实数.以下结论成立:
(ⅰ)系统(5)的每一个正解(yn,zn)满足当n=3k+i,i∈{1,2,3},k=1,2,…,
(ⅱ)如果
当n→∞,系统(5)的每一个正解(yn,zn)收敛于系统(5)的平衡点(0,0).
(ⅲ)如果
那么(0,0)与
$\left( {\sqrt[3]{{1 - p}}, \sqrt[3]{{1 -q}}} \right)$ 是不稳定的.证 (ⅰ)设{(yn,zn)}是系统(5)的正解.因为yn>0与zn>0,当n≥-2,由系统(5)推出
设vn,wn是下面系统的解,
使得
我们用归纳法证明
假设当k=m≥1,(12)式成立,那么由(9)式得
故(12)式是正确的.由(10)式与(11)式有,当n=3k+i,i=1,2,3,k≥1时
那么由(9),(12),(14)式可知(6)式成立.
(ⅱ)由(6)和(7)式,显然limn→∞yn=0,limn→∞zn=0.
(ⅲ)由(6)和(8)式,显然(0,0)是局部不稳定的.接下来证明平衡点
$\left( {\sqrt[3]{{1 - p}}, \sqrt[3]{{1 -q}}} \right)$ 是局部不稳定的.容易得到系统(5)关于平衡点$\left( {\sqrt[3]{{1 - p}}, \sqrt[3]{{1 -q}}} \right)$ 的线性化系统其中
这里
$\eta =- \sqrt[3]{{\left( {1 -p} \right){{\left( {1 -q} \right)}^2}}}$ ,$\beta =- \sqrt[3]{{{{\left( {1 -p} \right)}^2}\left( {1 -q} \right)}}$ .(15)式的特征方程为由(16)式有6×6矩阵
显然不是所有Δk>0(其中Δk,k=1,2,…,6,是矩阵∑6×6的k阶顺序主子式).因此由定理1.3.2[1]知正平衡解
$\left( {\sqrt[3]{{1 - p}}, \sqrt[3]{{1 -q}}} \right)$ 是局部不稳定的.定理2 考虑模糊差分方程(1),其中A,x-i,i=0,1,2是正模糊数.那么下面的命题成立.
(ⅰ)如果对任意α∈(0,1]使得
那么当n=3k+i,i=1,2,3,
$k \in {\mathbb{N}_ + }$ 时,方程(1)的每一个正解xn满足,(ⅱ)如果(17)式成立,那么当n→∞,方程(1)的每一个正解xn关于D收敛于平衡点x.
证 (ⅰ)设xn是方程(1)具有初始值x-2,x-1,x0的正解,使得
那么按照文献[6]命题2.1的方法,有
$\left( {{L_{n, \alpha }}, {\mathbb{R}_{n, \alpha }}} \right)$ ,n=0,1,…,满足下面带参数的常差分系统因(17)式满足,由引理3(ⅰ)知Ln,α与
${\mathbb{R}_{n, \alpha }}$ 满足(ⅱ)因(18)式成立,那么按照文献[6]的命题2.3的方法,有唯一的平衡点x,其中
设xn是方程(1)的正解,使得(18)式成立.因(17)式成立,应用引理3(ⅱ)于系统(19),有
由(21)式得
定理2(ⅱ)得证.
定理3 考虑模糊差分方程(1),若A是正实数(平凡模糊数)使得0 < A < 1,x-i,i=0,1,2是正模糊数.那么存在不稳定的平衡点0与
$x = \sqrt[3]{{1 -A}}$ .证 显然0是方程(1)的平衡点.对方程(1)的唯一正平衡点x,有下面的关系
由此有
应用引理3(ⅲ)于系统(19),平衡点0与
$x = \sqrt[3]{{1 -A}}$ 是不稳定的.
-
为验证结论的有效性,给出以下例子.
例 考虑三阶非线性模糊差分方程
其中A是正模糊数,且
初始值x-2,x-1,x0满足
由(25)式有
所以
$\overline {\bigcup\nolimits_{\alpha \in \left( {0, 1} \right]} {{{\left[A \right]}_\alpha }} } = \left[{1.2, 4.2} \right]$ .由(25)和(26)式,对α∈(0,1],
则
$\overline {\bigcup\nolimits_{\alpha \in \left( {0, 1} \right]} {{{\left[{{x_{-2}}} \right]}_\alpha }} } = \left[{0.2, 0.6} \right]$ ,$\overline {\bigcup\nolimits_{\alpha \in \left( {0, 1} \right]} {{{\left[{{x_{-1}}} \right]}_\alpha }} } = \left[{0.1, 0.5} \right]$ ,$\overline {\bigcup\nolimits_{\alpha \in \left( {0, 1} \right]} {{{\left[{{x_0}} \right]}_\alpha }} } = \left[{0.1, 0.4} \right]$ .由(23)和(27)式得含参数α∈(0,1]的差分系统
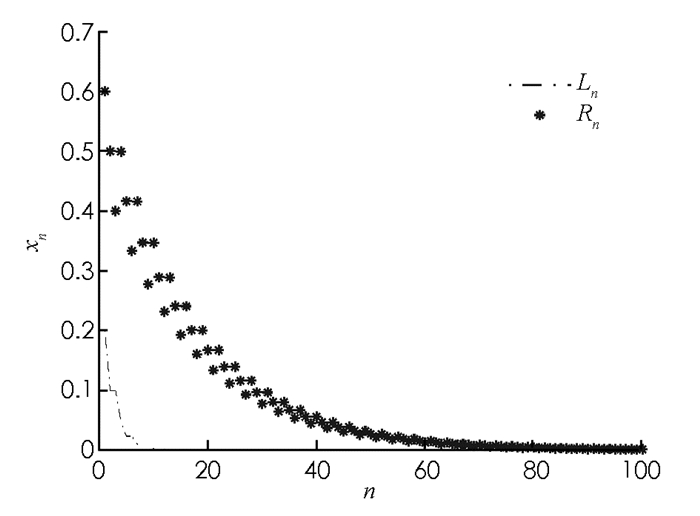
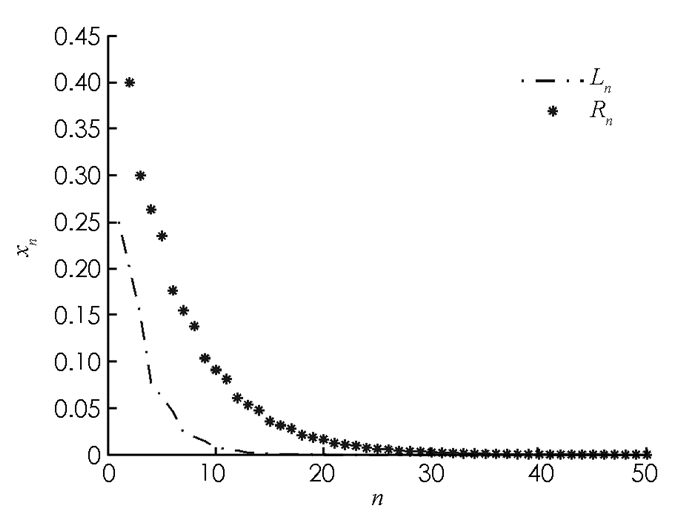
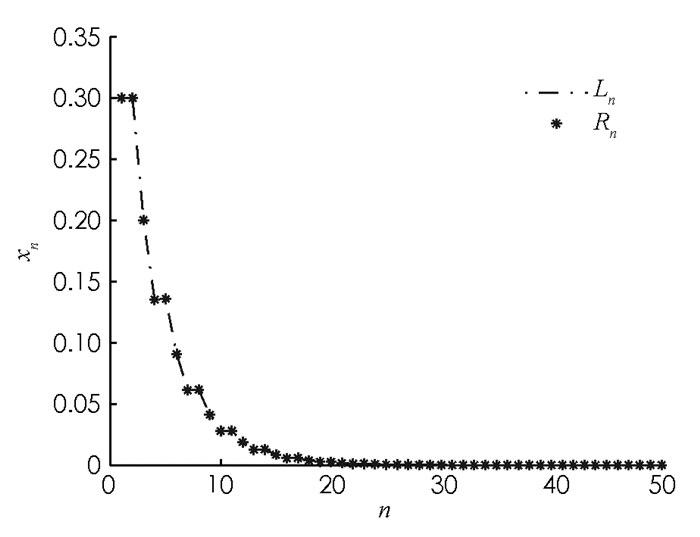
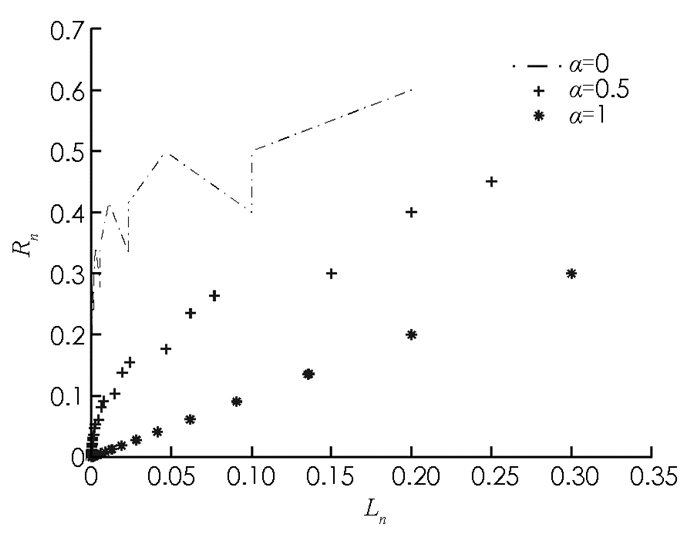
因此Al,α>1,对任意α∈(0,1],即条件(17)满足,所以由定理2,方程(23)的每一个正解xn是有界和持久的.另外,方程(23)有唯一平衡解
$\bar x = 0$ ,且当n→∞时方程(23)的每一个正解xn关于D收敛到唯一平衡点0(图 1-图 4).



 下载:
下载: