-
为了保证传输图像数据的真实性,近年来,学者们提出了多种水印方案[1-3],如Hosny等人[4]借助阿诺德映射来对水印信息进行置乱,然后利用精确极谐波变换处理载体图像,输出极谐波变换矩阵,通过水印嵌入方法,将置乱后的水印信息嵌入到极谐波变换矩阵中,从而完成水印的嵌入.但是,这种水印技术对混合几何攻击的鲁棒性较弱,且并不是所有的极谐波变换矩阵都适合嵌入水印,因此,其不可感知性较低.齐向明等人[5]将宿主图像分成互不重叠的图像块,并分析了每个图像块的纹理和边缘特征,但该技术是一种基于载体特征的水印方法,提取图像的特征点对图像修改比较敏感,且复杂度较高,在水印检测前,需要额外提取图像的特征点.如Wang等人[6]利用四元Fourier变换来处理彩色图像的R,G,B分量,以提取其实部的四元Fourier变换系数,通过对称水印嵌入方法,将水印信息嵌入到初始载体的四元Fourier变换系数中,获取水印图像,随后,根据最小二乘支持向量机来构建几何校正方法,增强水印图像的抗几何失真能力,实验结果验证了其算法的有效性.但该技术是将水印信息嵌入到所有的变换系数中,且其水印嵌入强度忽略了人眼视觉特性,使其不可感知性有待进一步提高,另外,其采用低阶伪Zernike矩来构建几何校正方法,因其不能有效提供载体的多尺度分析,而不能较好地描述载体的鲁棒特征,导致其抗几何失真能力有待提高. Wang等人[7]设计了基于非下采样Shearlet变换和极谐变换矩的图像水印方案,通过非下采样Shearlet变换,可以提供载体图像的近似最优逼近,确认水印的嵌入位置,将二值水印嵌入其中,并利用极谐变换矩阵来预测几何失真变换参数,对攻击水印图像完成校正.但在其水印嵌入过程中,没有考虑像素的水印嵌入强度,使其不可感知性不理想,且其采用的极谐变换系数模并非是载体的鲁棒特征,使得几何校正机制的能力受限.
为了改善水印算法的鲁棒性,并兼顾其不可感知性,本文根据文献[6]的四元Fourier变换思想和几何校正思想,在频域内,提出了新的彩色图像水印方案.通过仿射映射的预处理,混淆二值水印信息,增强其不可感知性;同时,利用四元离散Fourier变换处理彩色载体的最大中心区域,并根据其输出的实部系数矩阵,基于水印融入机制,把加密水印植入到宿主的低频像素中;同时,利用BKF(bessel K Form)分布的形状与尺度参数来训练SVM,以恢复被修改的水印数据内容.通过多组实验来验证该水印算法的抗几何失真能力与不可感知性.
全文HTML
-
四元数是一个复数的推广,它可表示为具有一个实部和3个虚部的四维复数,其模型如下[8]:
其中,w,x,y,z均为实数;i,j,k为虚部矢量,三者之间的关系如下:
由于彩色图像f(x,y)包含了R,G,B 3个分量,因此,也可以利用四元数来充分描述三者之间的关系:
其中,fR(x,y),fG(x,y),fB(x,y)分别是f(x,y)的R,G,B分量.
Fourier变换是将图像从空域转换到频域,可较好地反映像素的灰度变化,是图像信号处理的常用方法[9].为了拓展Fourier变换的优势,Ouyang等人[9]将四元数与Fourier变换结合,提出了四元离散Fourier变换,并将其用于图像信号处理[9]中:
其中,f(u,v)是彩色图像f(x,y)的四元离散Fourier变换结果;MN表示f(x,y)的尺寸为M ×N.
依据文献[9]可知,式(4)对应的可逆变换为:
为了展示式(4)的四元数特点,将其转变为如下模型:
其中,A(u,v)是彩色图像f(x,y)的四元离散Fourier变换对应的实部;C(u,v),D(u,v),E(u,v)则是相应的虚部.
-
由于多尺度多分辨率特征,小波变换被广泛用于图像水印、图像加密等领域.但是,传统的图像小波变换容易受到图像平移的影响,使其鲁棒性不佳,为此,本文引入四元小波变换来解决此不足,它具有近似平移不变性和丰富的相位信息.对于图像f(x,y),其四元小波变换函数fA(x,y)如下所示:
其中,fD(x,y)是离散小波变换结果;H1,H2是部分Hilbert变换;HT是总的Hilbert变换.
利用四元小波变换处理f(x,y),输出系数矩阵Q为:
其中,L代表低频;H代表高频;φ()是尺度函数;ϕ()是小波函数.
在式(8)中,每一行均对应一个四元数:
对于尺寸为M×N的初始图像f(x,y),经过l级的离散小波变换分解后,得到一个(22-lM)(22-lN)维的系数矩阵Q.以图 1(a)为对象,对其进行二级离散小波变换分解,其实部与3个虚部分别见图 2(a)-图 2(d).
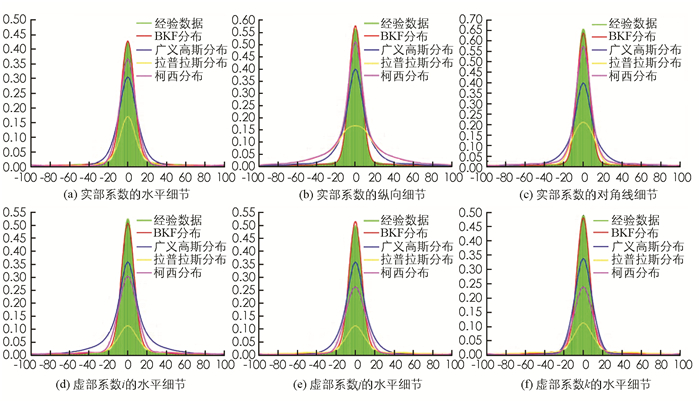
图像特征的多尺度表示是很重要的.随着多尺度几何分析在许多领域中的广泛应用,国内外学者提出了大量的统计模型,统计模型的目的就是用少量的统计参数来描述图像的分布特征,当前,较为成熟的统计模型有:广义高斯分布、柯西分布、拉普拉斯分布以及BKF分布[12].为了利用载体图像的鲁棒特征来训练SVM机制,需要选择出四元小波变换子带系数的最佳拟合分布.在本文中,选择二级四元小波变换的6个高通子带进行测试分析,包括实部系数的水平、纵向以及对角线细节,和虚部系数的水平细节. 图 3显示了二级四元小波变换的6个高通子带的经验直方图的拟合结果.依图可知,BKF分布可以最好地拟合四元小波变换子带对应的经验直方图.因此,本文选用BKF分布的形状与尺度参数来表示图像的鲁棒特征.
根据文献[13]可知,BKF分布的概率密度函数为
其中,p>0,c>0分别是拟合分布的形状、尺度参数;Γ(t)=∫0∞e-uut-1du;K()是改进的贝塞尔函数[14].
依据形状、尺度参数,BKF分布的特征函数可表示为
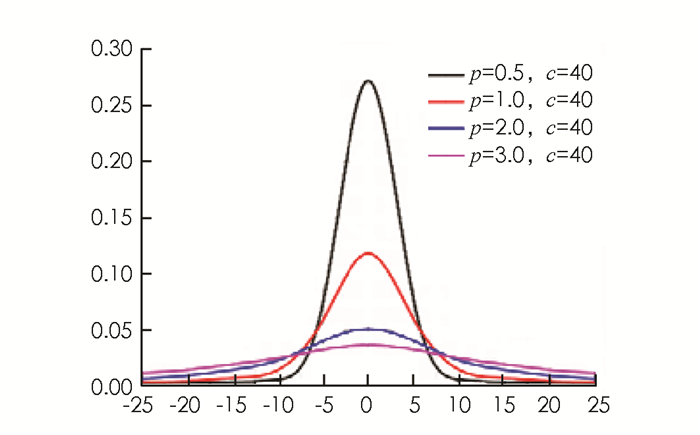
根据上述公式可知,当p=1时,式(11)是一个双指数概率密度函数;当p>1,式(11)接近高斯分布;当p<1,式(11)的分布呈现尖峰形态.不同的形状参数对应的BKF分布形态见图 4.
1.1. 四元离散Fourier变换[8-9]
1.2. 四元小波变换[10-11]
-
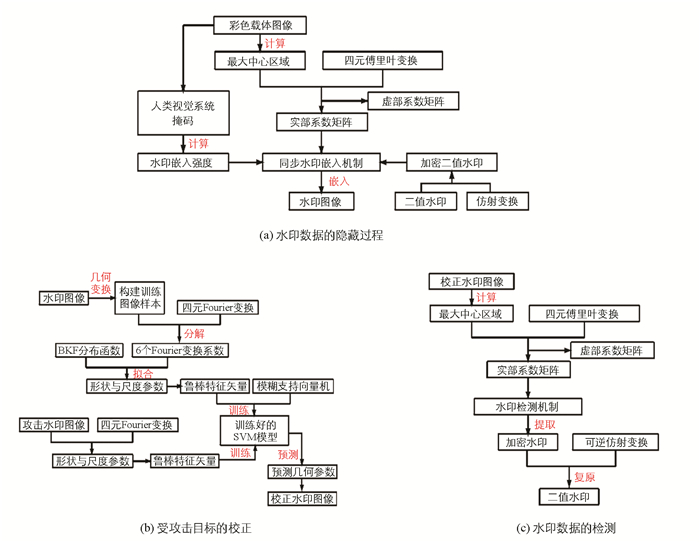
本文所设计的彩色水印方案的数据隐藏过程如图 5所示,主要分为水印数据的嵌入、同步校正与水印检测3个步骤.
-
1) 令I={f(x,y),0≤x<M,0≤y<N}是尺寸为M×N的彩色载体图像.其中,f(x,y)是(x,y)位置处的像素值. W={w(i,j),0≤i<P,0≤j<Q}是二值水印,尺寸为P×Q,且w(i,j)∈[0, 1].为了改善算法的不可感知性,本文通过仿射变换[15]来混淆二值水印,充分破坏其像素空间关系.其中,仿射映射为
其中,(x,y)、(x′,y′)分别是加密前后的像素点坐标;a,b,c,d都是变形系数;e,f是平移系数.
通过式(12)的置乱后,可获取加密水印W′={w′(i,j),0≤i<P,0≤j<Q}.
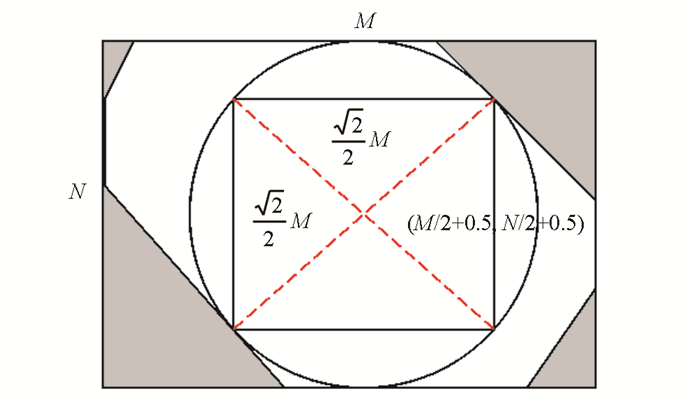
2) 由于图像经过一系列的旋转与反向旋转后,图像的边缘像素通常会丢失.为了改善水印图像的鲁棒性,本文计算出载体图像的最大中心区域,该区域内被旋转与反向旋转操作后,不会丢失像素,具有较高的稳健性.对图像旋转45°时,可获取其最大中心区域,见图 6.为了便于后续的表述,用IC={g(x,y),0≤x,y<t}来表示最大中心区域,其中,t=
$\sqrt {2} $ /2min(M,N).3) 随后,利用四元离散Fourier变换章节的内容,处理最大中心区域IC,输出一个实部系数矩阵A和3个虚部系数矩阵C,D,E.
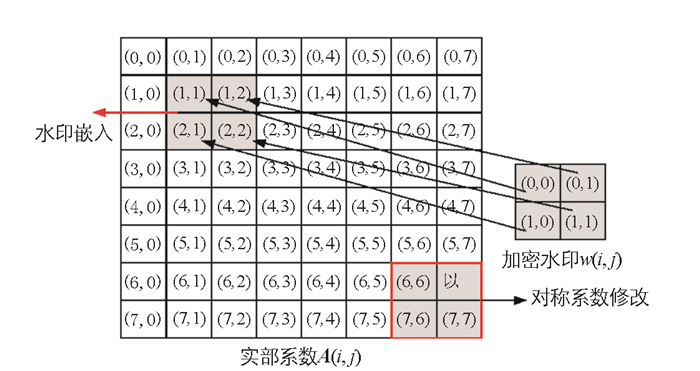
4) 人眼对四元离散Fourier变换的高频信息较为敏感,当把二者水印信息嵌入到这些高频系数中时,会导致其不可感知性较低.因此,在本文算法中,将二值水印嵌入到四元离散Fourier变换的低频系数中.根据四元离散Fourier变换理论可知,当水印图像经过可逆四元离散Fourier变换处理后,其仍需表示为一个纯四元数形式,使其在RGB颜色空间能够传输高质量的水印图像.所以,为了得到彩色水印图像的纯四元数形式,除了将水印嵌入低频系数A(i,j)之外,还必须修改对称四元数傅立叶变换的实部系数A(L-i,L-j),见图 7.根据文献[6],本文设计了同步水印嵌入方法:
其中,A(i,j)代表初始的四元离散Fourier变换系数;A′(i,j)是嵌入水印后的四元离散Fourier变换系数;Δ为水印强度因子;w′(x,y)为加密水印信息;L为系数矩阵的维数.
在进行式(13)的数据隐藏过程中,Δ值的大小对水印性能影响较大.为了兼顾良好的隐秘性与鲁棒性,本文引入人眼视觉系统HSV[16-17]来优化Δ.基于HSV嵌入强度Δ可自适应于彩色图像的特征,以确保最高的透明性.为此,根据彩色图像I的亮度ML、纹理MT与边缘掩码,获取嵌入强度Δ:
其中,ρ∈[0.4,0.5]是权重因子;ML为亮度掩码;MT为纹理掩码;I是彩色载体;EDI()是常见的边缘算子;EDE()是扩展操作;F是滤波操作;Z为HSV掩码.
本文利用HSV掩码来控制水印的嵌入强度Δ.将图 8(a)作为对象,其对应的ML,MT以及EDI分别见图 8(b)-8(d).最终形成的HSV掩码见图 8(e).
-
为了确保提取的二值图像无失真,本文联合QWT(Quaternion Wavelet Transform)与FSVM(Fuzzy Support Vector Machine)方法[17],来恢复受攻击的水印图像.令水印图像为I′{f′(x,y),0≤x≤M′,0≤y≤N′}.则失真校正步骤为:
1) 形成训练数据库.为了充分训练FSVM,需构建合适的训练图像集Hk(k=0,1,2,…,K-1).首先,将3种内容修改类型施加于彩色水印图像,从而形成了训练样本库Ωk.这些几何失真类型的参数分别用txk,tyk,Sk,θk来表示.其中,tx,ty是沿着X,Y轴的运动距离;S是尺度因子;θ为旋转角度.
2) 利用QWT,对这些训练图像Hk(k=0,1,2,…,K-1)进行二级分解;
3) 根据图 3所示的6个高通子带的BKF分布的形状和尺度参数,建立特征矢量p1k,c1k,p2k,c2k,p3k,c3k,p4k,c4k以及p5k,c5k,p6k,c6k.再联合几何失真参数txk,tyk,Sk,θk,形成了相应的训练样本,
4) 把训练样本Ω作为FSVM的输入矢量,对FSVM实施训练,最终得到参数值tx′k,ty′k,S′,θ′k.根据预测结果,对受到攻击的彩色水印图像完成校正.
为了验证所提校正方法的预测精度,从USC-SIPI数据集[18]中任意选择一幅彩色图像作为此次试验的对象,见图 9(a);再利用如下几何失真类型对其修改:10°的旋转攻击、沿Y轴平移15个单位、X与Y轴同时移动15个单位、缩放比例为0.5,输出一组训练数据集,如图 9(b)-9(e)所示.再利用这些数据来训练FSVM,以恢复遭受内容修改的水印图像.
再次从USC-SIPI数据集中挑选彩色样本Barbara实施恢复测试,如图 10(a)所示,再对其施加表 1中的内容修改类型,得到的数据见图 10(b),10(d),10(f),10(h).通过校正过程,得到的恢复图像见图 10(c),10(e),10(g),10(i),其预测的参数见表 1.由表 1数据和图 10可知,所提的几何校正机制能够准确恢复攻击图像,且预测误差较小.
-
通过稳定几何失真校正方法处理后,可获取正确的水印图像为I*.随后,通过如下水印提取方法,将二值水印从I*中检测出来,步骤如下:
1) 根据图 6所示,计算I*的最大中心区域Ic*={g*(x,y),0<x,y<t};
2) 利用四元Fourier变换处理最大中心区域Ic*,输出实部系数矩阵A*和3个虚部系数矩阵C*,D*,E*;
3) 根据如下水印提取方法,从实部系数矩阵A*中的低频系数中复原加密水印:
4) 通过式(18),可获取加密水印W*={w*(i,j),0<i<P,0<j<Q};随后,对W*进行可逆仿射变换,获取二值水印.
2.1. 水印数据的隐藏
2.2. 稳定几何失真校正机制
2.3. 水印信息的提取
-
基于Matlab软件完成该算法的性能测试,同时,为了体现该方案的先进性,将文献[4-6]当作对比组.仿真条件为:DELL vostro1088,3GHz,双核CPU,400GB硬盘以及4G内存.为了兼顾一般性,从USC-SIPI数据集中任意选择3幅彩色载体,见图 11(a)-11(c),尺寸均为256×256;同时,将图 11(d)-11(f)作为二值水印,其大小是64×64.其中,训练图像K=100,a=b=c=1,d=2,e=f=1.5;且选择RBF函数作为FSVM的核函数.衡量指标:(1)不可感知性;(2)鲁棒性.
-
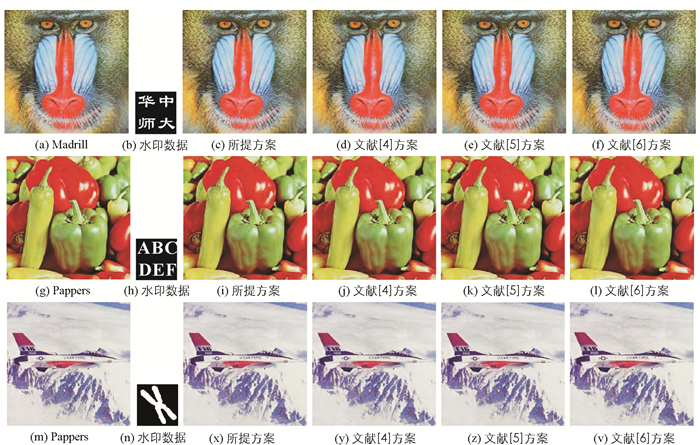
借助本文所提算法、文献[4]、文献[5]以及文献[6]的水印隐藏过程,把图 11(d)-11(f)分别嵌入到图 11(a)-11(c)中,输出的水印数据见图 12.根据水印结果可知,这4种方案都具备良好的不可感知性,非授权用户不能从中直接得到任何有用的线索.
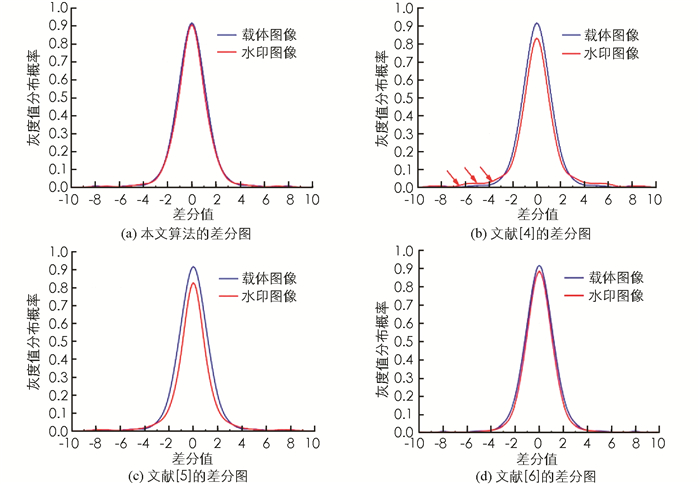
为了体现4种方案的差异,为此,本文利用差分图来客观量化所提算法与文献[4]、文献[5]、文献[6]的优劣,通过分析水印图像与初始载体的灰度分布拟合程度来评估.将图 12(a)、图 12(c)-12(f)视为对象,嵌入率为0.4 bpp,根据文献[3]的方法,输出的差分图曲线如图 13所示.根据测试数据可知,本文方法的水印图像对应的灰度分布与初始载体的拟合度最高,阶梯效应非常小,见图 13(a);文献[6]的差分图也比较理想,无明显的阶梯效应,与所提算法较为接近,但是,其水印图像的灰度分布不理想,见图 13(d).而文献[4]和文献[5]方法的差分图曲线不佳,分别见图 13(b)与图 13(c).原因是所提技术通过联合多种视觉因素来得到子块的量化步长,最大化了水印图像的不可感知性;并根据嵌入强度设计了同步水印嵌入方法,将加密的二值水印嵌入到彩色载体的四元Fourier变换低频系数中,对载体的修改范围较小.而文献[6]是将水印信息嵌入到整个图像的四元Fourier变换系数中,对载体图像的修改范围较大,而且水印嵌入过程中没有考虑人眼视觉特性,使其不可感知性要低于所提技术.文献[4]虽然也对二值水印进行了加密处理,但是,该技术是将水印信息嵌入到整个载体的极谐波变换矩阵中,忽略了人眼视觉特性,对载体图像的修改范围较大,导致其不可感知性不理想.文献[5]利用人类视觉系统的隐秘特性,对每个图像块的纹理特征和边缘特征进行分析,选择隐秘性好的图像块作为嵌入位置,并将加密后的水印信息嵌入到离散小波变换的低频系数中,具有较高的不可感知性.但是,此技术在水印嵌入过程中,没有考虑水印嵌入强度对水印结果的影响,采用经验值来完成水印嵌入,容易造成水印“溢出”或“下溢”的问题,使其隐秘性能要略低于所提技术.
-
为了突出所提技术的抗几何失真能力,以水印图像(图 9(c)-9(e))为样本,分别将方差为0.02的椒盐噪声攻击、45°的旋转、1倍的缩放、以及“旋转+缩放”的组合攻击施加给每幅水印图像,并基于本文所提算法、文献[4]、文献[5]和文献[6]的水印提取机制来复原二值水印,利用PSNR与NC来客观评价复原水印的失真度,数据见表 2.根据测试数据可知,4种技术所提取的二值水印与源水印数据间存在差异,然而,本文方案的鲁棒性最强,其提取的二值水印质量最高,对应的PSNR与NC值始终是最大的.文献[6]算法的抗几何失真能力比较强,要优于文献[4]和文献[5],其对应的PSNR与NC值始终与所提算法较为接近.而文献[4]、文献[5]的抗几何失真能力不佳,当水印图像被攻击时,二者所复原的二值水印均有不同程度的失真,对应的PSNR与NC值都要小于所提技术.主要是因为本文所提水印算法利用被攻击后水印图像的6个高通子带的BKF分布的形状和尺度参数作为特征矢量来训练FSVM模型,这些参数更适合描述图像特征,从而有效提高了二值水印的提取质量.而文献[6]与所提算法类似,都是构建了几何校正方法,将彩色载体的低阶伪Zernike矩阵作为特征矢量来训练最小二乘支持向量机LS-SVM模型,利用训练好的LS-SVM来预测几何失真参数,这些预测结果来校正水印图像,增强了二值水印的提取质量,但是,低阶伪Zernike矩阵无法提供图像的多尺度分析,使其不能很好地描述载体的鲁棒特征,使其几何校正能力要略低于本文所提算法.文献[4]则是利用水印图像的极谐波变换矩阵对应的不变性来抵御几何失真,但是,这种极谐波变换难以抵御混合攻击.文献[5]采用的SIFT技术对噪声攻击较为敏感,存在一定的伪特征点,且SIFT特征无法有效描述图像的分布特征,限制其稳健性.
3.1. 不可感知性测试
3.2. 鲁棒性测试
-
为了确保提取水印信息的质量,本文设计了多元频域变换与稳定几何失真校正的彩色图像水印算法.利用仿射变换来混淆二值水印图像,高度破坏其像素的空间关系,改善水印信息的隐秘程度.利用四元离散Fourier变换和四元小波变换,分别对彩色载体的最大中心区域进行频域变换和二级分解,降低图像对几何变换的敏感性;并根据系数分布函数对应的形状与尺度参数来构建训练样本,完成训练并恢复篡改水印图像的位置.测试数据表明了所提算法具有较高的鲁棒性与不可感知性,所复原的二值水印的失真度较小.




 下载:
下载: