-
在生存分析、环境科学分析、可靠性分析以及寿命测试分析中,数据通常呈现尖峰厚尾的特征,常见的伽马分布、对数正态分布、逆高斯分布和威布尔分布等对此类带有异常值的数据建模效果并不理想.针对这类问题,文献[1-3]通过添加新参数对一些常见的分布进行扩展得到一类新分布族,这类新分布族在建模上具有更好的灵活性.其中文献[4-6]使用这种扩展方法,基于林德利分布提出林德利一般分布(LG).本文对林德利—威布尔分布(LW)进行修正.LW分布使用威布尔分布作为基线概率密度函数,通过增加额外参数,提高林德利分布的适用性和灵活性.然而,LW分布的厚尾特征并不明显,不能对具有高峰度和异常观测值的数据集进行很好地拟合,为了解决这个问题,文献[7]引入含四参数的扩展林德利—威布尔分布(SLW),SLW分布具有比LW分布更宽的峰度范围,适用于具有非典型观测值的数据集.在这个基础上,本文提出了SLW分布的修正形式,即修正的扩展林德利—威布尔分布(MSLW).文献[8-10]指出,类似修正扩展分布更容易修改一些常见的分布,使其具有更高的峰度.因此MSLW与SLW分布相比具有更重的尾部,能更好地拟合带有异常观测值的数据,可以作为SLW分布的替代模型.
全文HTML
-
若随机变量X服从修正的扩展林德利—威布尔分布,记为X~MSLW(λ,α,θ,q),具体表达式为
其中:Z~LW(λ,α,θ)和U~exp(2)独立,λ>0是尺度参数,α>0和θ>0是形状参数,q>0是峰度参数.
-
命题1 假设X~MSLW(λ,α,θ,q),则X的概率密度函数表示为
其中λ>0是尺度参数,α>0和θ>0是形状参数,q >0是峰度参数,且有
证 根据随机表达式(1)和雅可比行列式的方法,计算X的概率密度函数如下:首先做一个变量替换,令
$X = Z{U^{ - \frac{1}{q}}} $ 以及T=U,则有$ Z = X{T^{\frac{1}{q}}}$ 和U=T,变换的雅可比行列式表示为因此,(X,T)的联合概率密度函数为
最后利用
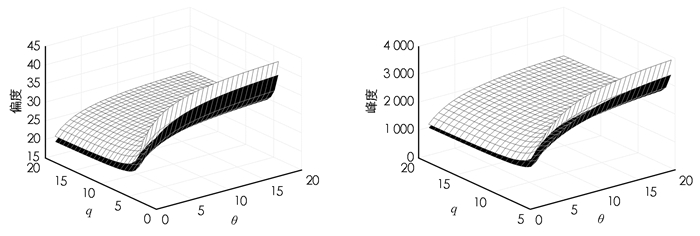
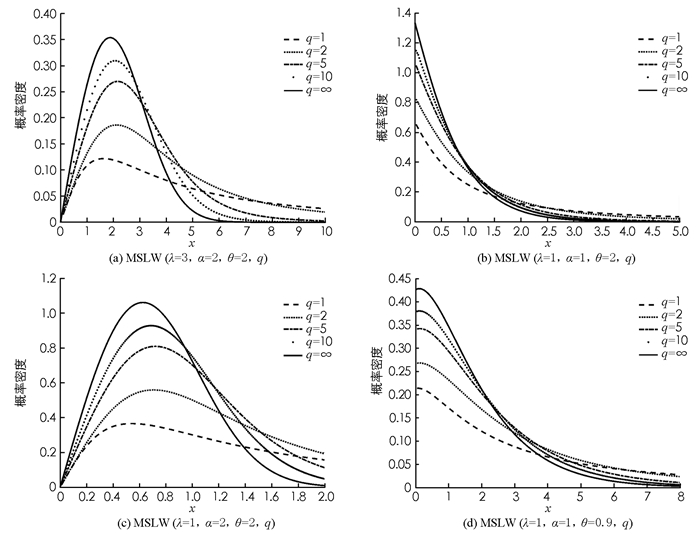
$u=\frac{x t^{\frac{1}{q}}}{\lambda} $ ,就得到X最终的概率密度函数.尺度参数λ,形状参数α和θ,峰度参数q对MSLW分布的概率密度函数的影响如图 1所示,呈现单峰或非增形状.
假设X~MSLW(λ,α,θ,q),那么由MSLW分布的概率密度函数的具体表达式,可以推导以下性质:
1)
$\mathop {\lim }\limits_{q \to \infty } {f_X}(x;\lambda , \alpha , \theta , q) = \frac{{\alpha {\theta ^2}}}{{\lambda (\theta + 1)}}{\left( {\frac{x}{\lambda }} \right)^{\alpha - 1}}\left[ {1 + {{\left( {\frac{x}{\lambda }} \right)}^\alpha }} \right]\exp \left( { - \theta {{\left( {\frac{x}{\lambda }} \right)}^\alpha }} \right) $ .2)
$ \mathop {\lim }\limits_{q \to \infty } {f_X}(x ; \lambda, 1, \theta, q)=\frac{\theta^{2}}{\lambda(\theta+1)}\left(1+\frac{x}{\lambda}\right) \exp \left(\frac{-\theta x}{\lambda}\right)$ .3)
$ F_{X}(x ; \lambda, \alpha, \theta, q)=\frac{2 \alpha \theta^{2} q \lambda^{q}}{\theta+1} \int_{0}^{x} v^{-(q+1)} J_{X}(v ; \lambda, \alpha, \theta, q) \mathrm{d} v$ .注1 (ⅰ)当q=1时,称X服从典型的修正的扩展林德利—威布尔分布,表示为X=ZU-1,记为X~CMSLW(λ,α,θ),并且其概率密度函数为
其中λ>0是尺度参数,α>0和θ>0是形状参数,JX由(3)式给出.
(ⅱ)由性质1)可知,当
$ q \to \infty $ 时,MSLW分布收敛到一般的LW分布[4];性质2)可知,当$ q \to \infty $ 且α=1时,MSLW分布收敛到林德利指数分布[11]. -
可靠性函数和风险率(失效率)函数是两项重要的可靠性指标.其中可靠性函数RT(t)表示一个项目在某个时间t内未发生故障的概率,定义为RT(t)=1-FT(t).MSLW分布的可靠性函数由下式给出
假定某事件的存活时间达到时刻t,那么该事件的风险率函数
$ h_{T}(t)=\frac{f_{T}(t)}{1-F_{T}(t)}$ 可以粗略地解释为在超过时刻t瞬时死亡的条件概率.MSLW分布的风险率函数如下其中JX由(3)给出.不同的参数λ,α,θ,q的取值下,MSLW分布的可靠性函数和风险率函数如图 2所示.由图 2可知,不同的参数取值下,MSLW分布的两种可靠性指标函数表现出多种图形形状,这说明了新的分布MSLW的灵活性.
-
引理1 设Z服从LW(λ,α,θ)分布,则有
其中
$ \varGamma\left(\frac{r}{\alpha}\right)$ ,表示为伽马函数,见文献[7].命题2 设X服从MSLW(λ,α,θ,q)分布,那么,对于r=1,2,…,以及q>r,X的r阶矩如下
其中
$ d(r)=\left(\alpha+\frac{r}{\theta+1}\right) \varGamma\left(\frac{r}{\alpha}\right) \varGamma\left(\frac{q-r}{q}\right)$ .证 由(1)可知,Z和U是相互独立的两个随机变量,所以就有
其中
$ \mathbb{E}\left(U^{-\frac{r}{q}}\right)$ 经计算为$ 2^{\frac{r}{q}} \varGamma\left(\frac{q-r}{q}\right), q>r $ ,$ \mathbb{E}\left(Y^{r}\right)$ 由(6)式给出.推论1 若X~MSLW(λ,α,θ,q),则有
1)
$ \mu_{1} =\mathbb{E}(X)=\frac{2^{\frac{1}{q}} \lambda}{\alpha^{2} \theta^{\frac{1}{\alpha}}} d(1) $ 2)
$ \mu_{2} =\mathbb{E}\left(X^{2}\right)=\frac{2^{\frac{2}{q}} 2 \lambda^{2}}{\alpha^{2} \theta^{\frac{2}{\alpha}}} d(2), q>2 $ ;3)
$\mu_{3} =\mathbb{E}\left(X^{3}\right)=\frac{2^{\frac{3}{q}} 3 \lambda^{3}}{\alpha^{2} \theta^{\frac{3}{\alpha}}} d(3), q>3 $ ;4)
$\mu_{4} =\mathbb{E}\left(X^{4}\right)=\frac{2^{\frac{4}{q}} 4 \lambda^{4}}{\alpha^{2} \theta^{\frac{1}{\alpha}}} d(4), q>4 $ ;注2 偏度和峰度系数由下面两个式子给出
由推论1可知,MSLW分布的偏度和峰度系数值独立于尺度参数λ.
图 3表示形状参数α=0.3的MSLW分布和SLW分布的偏度和峰度系数,由图 3可知MSLW分布的两个系数值均大于SLW分布,可用于拟合具有异常观测值数据的分布.
1.1. 随机表达式
1.2. 概率密度函数
1.3. 可靠性分析
1.4. 分布的矩
-
本节阐述MSLW分布参数估计的最大似然(ML)方法.若X1,X2,…,Xn是来自服从MSLW(λ,α,θ,q)分布,容量为n的随机样本.假设参数未知,其中
$x_{1}, x_{2}, \cdots, x_{n} $ 表示观察值,则对数似然函数为其中
$ c(\lambda , \alpha , \theta , q)=n\log \left( \frac{2\alpha q}{\theta +1} \right)+2n\log (\theta )+nq\log (\lambda ), {{J}_{X}}(x)={{J}_{X}}(x;\lambda , \alpha , \theta , q)$ 由(3)式定义.在实际中,为了得到参数的ML估计,本文选用数值方法求解优化问题其中l(λ,α,θ,q)由(9)式给出.本文使用R软件中optim函数,应用L-BFGS-B算法来求解(10).文献[7]指出,两个形状参数α和θ的存在导致参数可识别性的问题,但如果只有一个形状参数,这个问题就会消失.因此,出于实际目的,在实证分析中,本文使用具有唯一形状参数的MSLW模型版本,即假定α=θ.
-
本节比较4种分布MSLW,MSL,SLW和LW对具有较高峰度的实际数据集建模的有效性.数据来源于http://lib.stat.cmu.edu/datasets/Plasma_Retinol,该数据表明人体中一些微量营养素的血浆浓度存在很大差异,可能会增加某些癌症发生的风险,其包含了14个变量,每个变量下有314个观测值,本文选择其中第13个变量β-血浆进行分析.
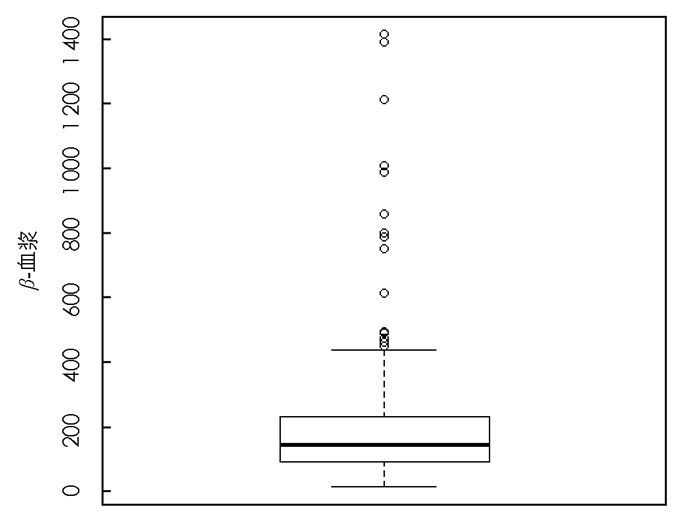
表 1是对β-血浆数据进行描述性统计分析的一个总结,其中n表示样本容量,
$ {\bar{x}}$ 为样本均值,S2为样本方差,βs和βk分别表示样本的偏度和峰度系数,揭示了数据具有较高的峰度,也可以更直观地在箱线图(图 4)中看出.表 2分别给出了4个模型MSLW,MSL,SLW和LW的参数的最大似然估计以及相应的最大对数似然函数值,表明MSLW模型对应的对数似然函数值最大.
为了比较分布的拟合效果,本文考虑Akaike信息准则(AIC)和Bayesian信息准则(BIC).它们分别表示为
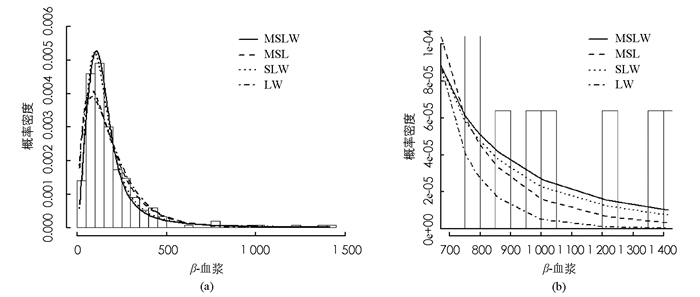
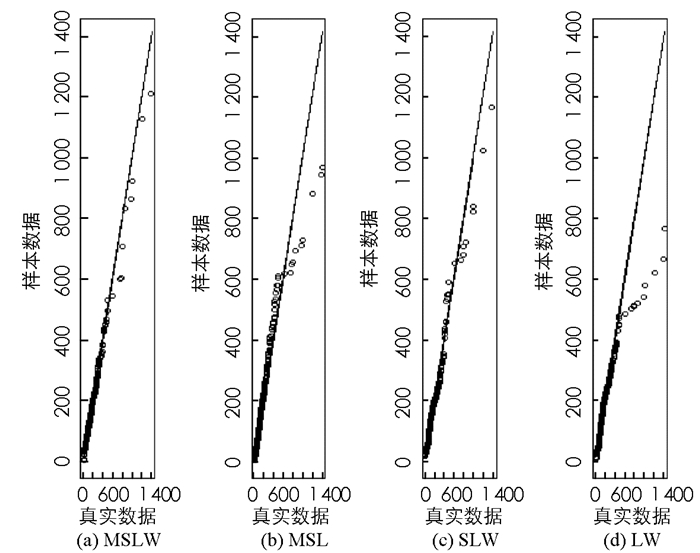
其中:k为分布参数个数,n为样本容量,log lik为对数似然函数的最大值.表 3显示了每个模型对应的AIC和BIC值,以及应用拟合优度Kolmogorov-Smirnov进行检验得到的Kolmogorov-Smirnov统计量(K-S统计量)和检验的P值.可以看出,基于AIC,BIC,K-S统计量和P值,MSLW模型比另外3个模型的拟合效果更好.除此之外,可以更直观地在图 5(a)发现,对于真实数据,MSLW拟合程度更优.图 5(b)直方图尾部的放大图揭示了MSLW分布对具有较高峰度的数据集适用性更强.图 6分别描述了MSLW,MSL,SLW和LW同原始数据的Q-Q图,也同样表明MSLW模型在该数据集上具有更好的拟合效果.
-
引入了LW分布的一个新的扩展形式,新分布表示为LW分布和指数分布的幂这两个独立随机变量的比值,称为修正的扩展林德利—威布尔分布(MSLW).该分布扩大了峰度范围,可用于模拟具有过度峰度和异常观测值的正数据集,实证分析验证了该分布的可行性.



 下载:
下载: