-
针对实际问题,背包问题[1]可构造出一系列子问题,如0-1背包问题[2]、有界背包问题[3]、折扣{0-1}背包问题[4]等.目前求解有界背包问题(BKP)的方法有精确算法和近似算法[5-7].
本文在标准萤火虫算法的基础上结合混沌理论和小生境技术提出混沌小生境萤火虫算法(NCFA)用于求解有界背包问题,并与小生境萤火虫算法(ULFA)、带权重的贪心萤火虫算法(WGFA)[8]进行对比实验,结果表明本文算法能有效解决有界背包问题.
全文HTML
-
有界背包问题[3]是组合优化中经典的NP问题之一,其具体描述如下:
考虑背包问题中的背包容量为C,使用n项特定的物品来填充它,其中第i项物品价值为pi,对应重量为wi,可选择物品个数最多为bi,现选择若干个物品,在保证总重量不超过背包容量C的情况下使得背包内物品的价值总和最大.有界背包问题的数学模型如下:
其中:系数pi,wi,bi(i=1,2,…,n)和C均为正整数.
-
萤火虫算法[9]是基于萤火虫闪光行为的一种启发式算法.萤火虫的吸引度取决于它的亮度,亮度越强吸引度就越强,因而可以将萤火虫亮度与有界背包问题的目标函数相关联,可将目标函数值直接作为萤火虫xi(i=1,2,…,n)的亮度:
同时萤火虫的一部分亮度在传输过程中会被介质吸收.在最大化问题中,萤火虫相对亮度较低者会被相对亮度较高者吸引,相对亮度受萤火虫自身亮度和距离影响,其描述如下:
其中:γ为光强吸收因子,r为两萤火虫之间的欧式距离.两只萤火虫间的吸引度也将随着萤火虫i和萤火虫j之间的距离rij变化而变化.因此,可以定义萤火虫的吸引度β为
其中:β0为萤火虫在距离为r=0时的吸引度,γ为光强吸收因子,r为两萤火虫之间的欧氏距离.若萤火虫i向萤火虫j的方向移动,移动公式如下:
其中:xit,xjt为萤火虫i和萤火虫j在第t代时所处的位置;α为步长因子,rand为一个从0到1均匀分布的随机数,αrand-12为随机搜索项.
-
混沌是自然界广泛存在的一种非线性现象,具有随机性、遍历性、初始条件敏感性等特点[10],本文采用的混沌映射是立方映射[11],其表达式为:
实际问题中,在初始值不为0的情况下都会产生混沌,对比logistic映射,立方映射产生的混沌序列均匀性较好,这里将其用于萤火虫种群的初始化.
-
Levy飞行[12]是一种随机漫步,其步长服从于一个重尾的概率分布,使用Levy飞行的位置更新如下所示:
其中:xit表示个体i在第t代的位置,⊕为点对点乘法,α为步长控制量,dLevy(λ)为随机步长,i=1,2,…,n.由于Levy飞行具有快速增长且方差无限的特点,于是运用于大规模搜索时,其搜索效果比较好[13].由于Levy飞行是短距离的探索和偶尔长距离的飞行相结合,所以若对更新后的萤火虫全部进行Levy飞行将不能保护优秀个体.本文为了使较差萤火虫得到充分利用,于是选取惩罚个体的
$\frac{1}{5}$ 进行Levy飞行.目的是种群在增加全局搜索能力的同时避免破坏较优个体. -
小生境技术[14]包含了共享机制与排挤机制.传统的小生境共享机制采用单一的共享半径与两个个体的距离进行比较,虽然能判断多个子群内的拥挤程度,但是并不能判断子群内个体的优劣.本文提出计算小生境内个体的共享函数如下
其中:fibest和fiavg分别表示个体i与最好个体的适应度差异和个体i与其他个体的平均适应度差异,e1和e2表示个体i的两种共享半径
种群内个体的共享适应度为
其中:n为种群内的个体数,dij为小生境内个体间的欧氏距离.为了保证种群多样性,本文根据共享适应度对所有个体进行排序,并对较差的部分个体进行惩罚:
其中penalty为惩罚系数.
-
为了使算法快速找到问题的最优解,本文利用每次迭代产生的除最优个体外前k个较优个体产生新的位置,并将其用于替换相等数量的最差个体,位置更新公式如下
其中:xnew为更新后的个体,xbest为最优个体,λ为一个属于(0,1)的随机数,xi为除最优个体外的前k个较优个体i=2,3,…,k+1.
-
由于有界背包问题是离散化问题,而萤火虫算法针对连续型问题求解,于是需要一种编码方式将问题中的连续解离散化,本文采用如下编码方式:
其中:bound(k)为背包内第k项物品的可选择数上限,xik为第i个个体的第k个分量,i=1,2,…n.
-
由于萤火虫算法在求解有界背包问题过程中会产生大量不可行解,本文采用文献[6]提出的一种改进贪心算法对不可行解进行修复.
2.1. 标准萤火虫算法
2.2. 混沌思想
2.3. Levy飞行
2.4. 小生境技术
2.5. 局部搜索
2.6. 编码方式
2.7. 对不可行解的修复处理
-
改进后的萤火虫算法(NCFA)用于求解有界背包问题实施步骤具体如下:
Step1 初始化参数,利用混沌理论对萤火虫种群初始化.
Step2 根据式(4)-(7)更新萤火虫位置,利用改进贪心算法修复不可行解.
Step3 根据式(10)-(13)计算Step2中解的共享适应度并排序,对共享半径内的较差个体进行惩罚.
Step4 对种群内被惩罚个体选取一定比例进行Levy飞行,并计算种群内萤火虫适应度.
Step5 利用局部搜索得到的新解替换较差解,利用改进贪心算法修复不可行解.
Step6 计算种群内个体适应度,更新全局最优值及最优解.
Step7 判断是否达到结束条件,若是,转Step8;若否,转Step2.
Step8 输出全局最优值.
-
本文利用3类BKP实例(UBKP,WBKP,SBKP)对混沌小生境萤火虫算法进行测试,每一类都包含10个规模在100~1 000的实例,所有实例数据均来自于文献[6].
本文仿真实验所用硬件环境为:AMD A6-3420M APU with Radeon (TM) HD Graphics 1.50 GHz,内存为4.0 GB,操作系统为64位Windows 7旗舰版.编程语言为MATLAB,编译环境为MATLAB R2018a,并使用MATLAB在编译环境中绘制折线图.
为了验证本文算法的有效性,对3类BKP实例进行仿真实验,并与其他两类算法(ULFA,WGFA[8])实验数据进行对比,其中ULFA是融合了小生境技术与改进贪心算子的萤火虫算法,将其作为测试本文算法的对比算法.各算法的参数设置见表 1.
表 1中γ为光强吸收因子,β0为吸引度,α为步长因子.为了直观比较各算法性能,本文将各算例分别独立运行50次,利用测试结果与理论最优值进行对比,并比较各算法间的最优值、平均值、最差值以及标准差.实验结果见表 2-4,其中Opt是理论最优值,Best是最优值,Mean是平均值,Worst是最差值,Std是标准差.
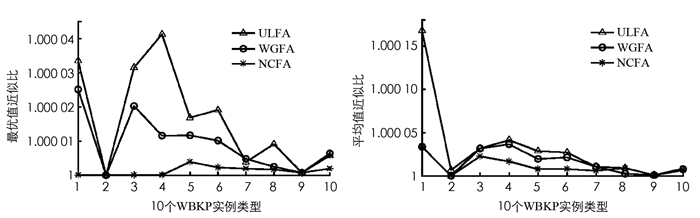
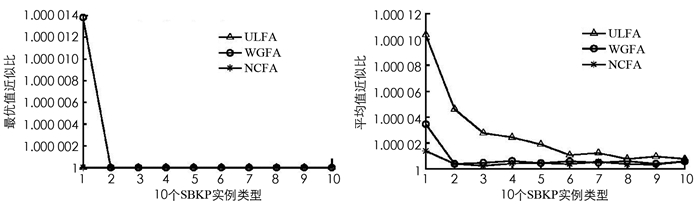
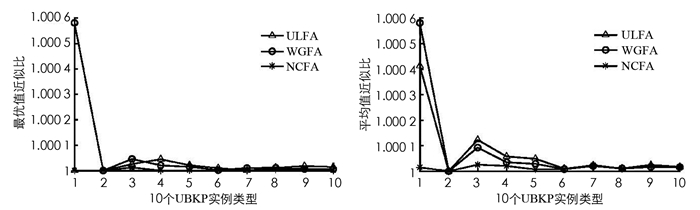
通过表 2-4可以看出3种算法用于求解不同类型的有界背包问题的结果.对于UBKP而言,第1,2,4,6,7,10例算例本文算法均可找到理论最优值,即使不能找到最优值,最终结果也会优于另外两种算法;对于WBKP而言,第1,2,3,4例算例本文算法能寻到理论最优值,除第9例算例外,其他各例均优于其他两类算法;对于SBKP而言,3种算法的寻优结果都较好.本文参考文献[6]的平均近似比和最佳近似比对以上3类算例进行对比,对比结果见图 1-3.
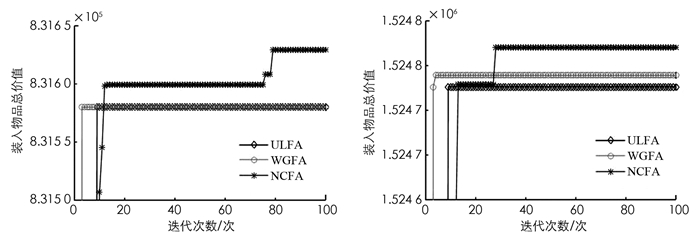
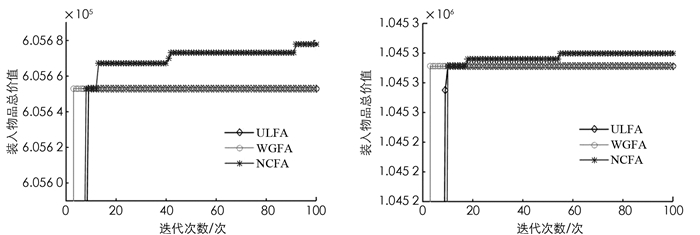
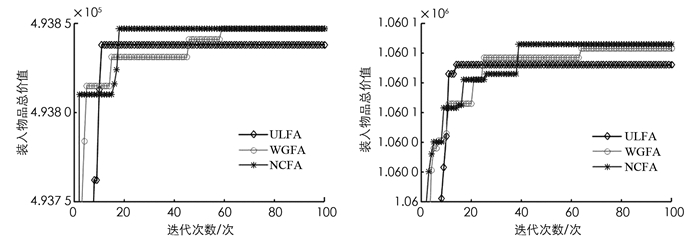
从图 1-3中3组算法针对3类问题的近似比可以看出,NCFA除了在计算WBKP实例8时的平均值近似比劣于其他两种算法外,其他近似比均优于另外两种算法,并且NCFA的近似比曲线较平稳,说明该算法用于求解BKP问题更有效.为了更直观比较3种算法寻优所需要的迭代次数,下面给出3种算法的平均收敛曲线(图 4-6).
从图 4-6收敛曲线可以看出,本文算法均能在100代内搜索到理论最优值,在求解WBKP7时能搜索到相对较优值,本文算法比WGFA更适合用于求解BKP,全局搜索能力更强,能有效跳出早熟区域寻找到理论最优值,可以作为求解BKP的有效算法.
-
本文在萤火虫算法基础上加入改进的小生境技术,在一定程度上增加了全局搜索能力,在算法初期利用混沌初始化得到的解均匀分布在解空间,并利用改进贪心算法增加了有效个体的数量,为后期寻找全局最优奠定了基础,基于萤火虫算法的改进算法NCFA可以有效求解BKP.



 下载:
下载: