-
图像和视频通信已经成为人们日常生活的重要组成部分,使用当前的图像捕获技术,噪声不可避免地在图像中产生,尤其是在低光照条件下获取的图像,最常见的噪声类型是加性白高斯噪声[1](Additive White Gaussian Noise,AWGN).由于噪声降低了图像的视觉质量和计算机视觉算法的性能,因此近年来图像去噪已经成为图像处理方面的热点问题.
图像去噪[2]要求在有效去除噪声和不引入人为特征(阶梯、振铃现象)的同时,尽可能地保留边缘信息和纹理细节.目前,图像去噪[3]方法大致可以分为空间域和变换域两类.空间域去噪以高斯滤波[4]、基于偏微分方程滤波[5]、双边滤波[6]等算法为代表,可以得到较高的峰值信噪比,但在边缘信息和纹理细节方面保留较少.变换域去噪以小波变换[7]、contourlet变换[8]、Curvelet变换[9]等方法为代表,可以很好地保留图像的几何信息,但是该类方法的计算较为复杂.
双边滤波(Bilateral Filter,BF)去噪算法具有容易实现且计算简单的特点,可以识别显著的边缘细节,在消除噪声的同时能够保留部分几何信息.但是,当噪声变大后,双边滤波的抑噪能力会变差. Chaudhury等[10]提出了加权双边滤波(Weigthed Bilateral Filter,WBF)方法,采用鲁棒双边滤波的预处理结果来引导标准双边滤波去噪,对有较大方差的噪声具有鲁棒性,但是由于采用了均值滤波,会使得图像在去噪过程中丢失一些纹理结构.芦碧波等[11]提出了一种利用全变分方式引导双边滤波器进行去噪的方法,该算法在去噪能力和边缘信息保持方面都有所提升,但是利用双边滤波在消除图像中高频部分噪声的同时,也会将分布在高频处的边缘纹理信息滤除. Curvelet变换是建立在小波变换和脊波变换的理论基础之上,继承了小波变换良好的时频分析能力和脊波变换的方向选择特性,能够更好地保持去噪图像的边缘信息,但是在重构过程中容易产生振铃效应和伪影现象.
针对WBF在边缘纹理方面保留不好的问题,通过结合空间域和变换域去噪方法的优点,提出了一种结合Curvelet变换与WBF的图像去噪方法.本文首先使用加权双边滤波器将噪声图像分解为低频图像和高频图像,然后对高频图像应用Curvelet变换,通过设定合适的阈值函数使得图像中保留更多的边缘纹理细节,最后将低频图像和处理后的高频图像进行重构,得到保存有更多几何信息的去噪图像.实验结果表明,相对于其他方法,本文方法在去噪性能方面有了明显的改善,在边缘信息保留方面也有实质性的提高,并且重构过程中避免了振铃、伪影现象的出现.
全文HTML
-
标准双边滤波(Standard Bilateral Filter,SBF)是一种非线性滤波器,可以达到保持边缘、降噪平滑的效果.双边滤波不仅考虑了像素的欧氏距离,还考虑了像素范围域中的颜色差异,其原理是将一个与空间距离相关的高斯函数和一个与灰度距离相关的高斯函数相乘.
其中,x表示像素位置,Ω为像素x的邻域,j是邻域Ω内的像素,I(x)和
$ {\hat I_1}$ (x)分别表示噪声图像和双边滤波后的输出图像,$ {f_{{\sigma _s}}}(x) = {{\rm{e}}^{\left( { - \frac{{{{\left| x \right|}^2}}}{{2\sigma _s^2}}} \right)}}$ 和$ {f_{{\sigma _r}}}\left( t \right) = {{\rm{e}}^{\left( { - \frac{{{{\left| t \right|}^2}}}{{2\sigma _r^2}}} \right)}}$ 分别表示几何邻近关系的空间滤波函数和灰度相似关系的灰度滤波函数,σs和σr表示高斯函数中的标准差,其大小决定了双边滤波器的性能.由于这两个参数与噪声方差有关,不是独立的,因此在鲁棒双边滤波器(Robust Bilateral Filter,RBF)中将这两个参数设置为单独可调整的值.
其中,
$ \bar I(x) = \frac{1}{{{{\left( {2L + 1} \right)}^2}}}\sum\limits_{j \in {{\left\{ { - L, L} \right\}}^2}} {I\left( {x - j} \right)} $ ,L用于控制平滑量.为了在所有噪声水平下获得最佳去噪性能,加权双边滤波器(Weighted Bilateral Filter,WBF)定义为标准双边滤波器和鲁棒双边滤波器的线性组合.
其中,θ1和θ2是最佳权重,一般通过去噪图像和原始图像之间的均方误差(Mean Squared Error,MSE)最小化方式求得.
-
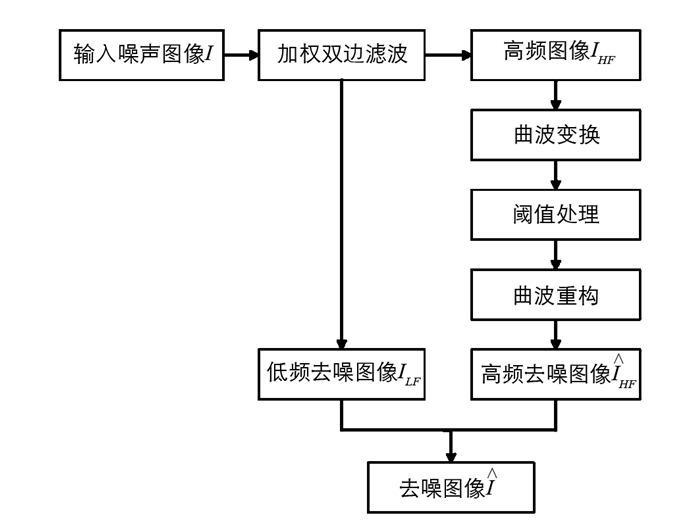
本文方法是在加权双边滤波器(WBF)的基础上,利用Curvelet变换进行去噪的方法.在实现过程中,使用加权双边滤波器将噪声图像分解为低频(Low Frequency,LF)部分和高频(High Frequency,HF)部分,低频图像是加权双边滤波器滤波后的图像,高频图像则需要经过Curvelet的阈值处理,获取分布在高频部分的几何信息,具体流程如图 1所示.
-
利用加权双边滤波器可以将噪声图像I分解为低频图像ILF和高频图像IHF,分解后的图像大部分信息保留在低频部分中,而边缘和纹理细节存在于图像的高频部分中.虽然加权双边滤波器在对噪声图像I平滑滤波的同时,可以利用平均像素方法保留部分的几何细节,但是丢失了大部分分布在高频部分的几何细节.
在处理过程中,WBF需要根据噪声图像I计算出最优权重系数θ1和θ2,然后利用均方误差(MSE)最小化方法估计权重系数.最后,根据公式(3)将噪声图像分解成低频图像ILF和高频图像IHF.
-
在图像处理中,大多数自然图像由曲线线条构成.相对于小波变换而言,Curvelet变换是一种具有高方向灵敏度的多尺度变换,可以很好地捕获到图像的曲线边缘,并且Curvelet变换只需很少的非零系数就能够准确地表示平滑函数和边缘信息.
本文采用第二代快速离散Curvelet变换中的Wrapping算法,该算法是基于特殊选择采样的傅里叶变换的卷绕.
利用二维傅里叶变换将给定的时域函数f[t1,t2]变换至频率域f[ω1,ω2].
对f[ω1,ω2]函数进行重采样
其中,l表示角度.
将插值后的fl与窗函数Uj[ω1,ω2]相乘
其中,j表示尺度.
围绕原点Wrapping局部化
对
$ {{\tilde f}_{j, l}}$ 进行二维傅里叶逆变换,得到离散Curvelet系数CD.Curvelet变换有很好的方向选择性,当选择的方向与图像边缘方向一致时,可以获得较大的图像系数,较小的噪声系数. Curvelet变换通过设定合适的阈值达到图像去噪的目的. Curvelet变换的阈值函数可以分为3种:
硬阈值函数定义为
其中,w和Sδ(w)表示Curvelet实际系数和估计系数,δ表示阈值.
软阈值函数定义为
其中,sgn表示符号函数.
在去噪过程中,硬阈值函数在阈值处不连续,重构信号可能会出现跳跃现象;软阈值函数在|Sδ(w)|>δ时,Sδ(w)与w存在差异,对接近实际信号有很大影响.因此,本文采取软、硬阈值函数相折衷的方式.
其中,0≤α≤1.采取软、硬阈值函数相折衷的方式可以有效避免上述问题的出现,去噪效果更显著,图像纹理更清晰,高频细节更突出.
基于Curvelet变换的阈值去噪方法可以分成3个步骤:
1) 对高频噪声图像进行曲波变换,得到不同尺度上的Curvelet系数;
2) 采取折衷阈值函数,对Curvelet系数做阈值处理;
3) 利用曲波逆变换对阈值处理后的Curvele系数进行重构,得到去噪图像.
-
将高频滤波图像
${\hat I_{HF}} $ 和低频滤波图像ILF融合成一幅图像$ \hat I$ .与采用加权双边滤波器进行去噪的图像ILF相比,本文方法的去噪图像
$ \hat I$ 具有更多的边缘信息和纹理细节.
2.1. WBF图像分解
2.2. 基于Curvelet变换的图像细节保留
2.3. 图像融合
-
所有实验在一台配置为Intel(R) Core(TM)i5-3320 CPU @2.60 GHz和4 GB RAM的笔记本电脑上进行,所有测试均在Matlab 2014a环境下实现.选取数字图像处理常用数据集Set12进行实验,Set12数据集包括Lena,Cameraman,Barbara,House等在内的12张灰度图像,尺寸为256×256.将测试结果与标准双边滤波(SBF)、加权双边滤波算法(WBF)、LPG-PCA、Curvelet变换、WBF+Wavelet和Curvelet-双边滤波联合算法(JBF+Curvelet)等算法进行对比分析.
所有实验中主要是对常见的加性高斯白噪声进行研究处理,通过设定不同的噪声方差(σ=10,20,50),对比所提出的方法和其他方法的去噪性能.加权双边滤波器(WBF)的分解过程主要通过选择两个参数σs和σr的窗口大小来控制.本文算法选择的参数为空间内核σs=4,范围内核σr=20和窗口尺寸为11×11.
-
为了评价算法的去噪性能,采用图像处理中常用的3种指标进行估计:峰值信噪比(PSNR)、结构相似性指数(SSIM)和视觉信息保真度(VIF).
PSNR表示滤波图像的最大像素值与噪声的比值,定义为
其中MSE表示均方误差,fmax和fmin分别表示去噪图像的最大像素和最小像素. PSNR越大,说明去噪图像失真越小,图像的去噪效果越好.
基于感知模型的归一化度量SSIM定义为
其中,
$l\left( {x, y} \right) = \frac{{2{u_x}{u_y} + {c_1}}}{{u_x^2 + u_y^2 + {c_1}}}, c\left( {x, y} \right) = \frac{{2{\sigma _x}{\sigma _y} + {c_2}}}{{\sigma _x^2 + \sigma _y^2 + {c_2}}}, s\left( {x, y} \right) = \frac{{{\sigma _{xy}} + {c_3}}}{{{\sigma _x}{\sigma _y} + {c_3}}} $ 分别表示亮度比较、对比度比较和结构比较,x,y分别为参考图像和去噪图像,ux,uy分别表示图像x,y的均值,σx2,σy2表示x,y的方差,σxy表示x,y的协方差,c1,c2,c3为很小的常数. SSIM从亮度(均值)、对比度(方差)和结构3个层次比较图像失真,但经常用于比较去噪图像与原始图像间的结构相似形,SSIM在[-1, 1]区间范围内取值,其值越接近1,说明两者结构相似性越好,相反相似性越差.VIF通过计算去噪图像与原始图像之间的互信息来衡量去噪图像的质量优劣,该指标与主观视觉具有更高的一致性, VIF可以定义为
其中,M表示小波分解的子带个数,
$ {{{\overrightarrow C }^{N, j}}}$ 表示第j个子带上随机场的N个元素,$ {{{\overrightarrow E }^{N, j}}}$ 和${{{\overrightarrow F }^{N, j}}} $ 分别表示原始图像和失真图像的人类视觉系统模型的输出. VIF值越大,表明图像质量越好. -
使用RBF、WBF、LPG-PCA、Curvelet变换、WBF+Wavelet、JBF+Curvelet和本文算法在加入标准差σ=30的高斯白噪声后,不同算法获得的去噪图形PSNR值分别对应20.87,27.92,28.85,28.36,28.59,28.70,29.68 dB,从而说明本文算法比其他算法具备更优的去噪性能.可以更好地保留图像中的纹理细节和边缘信息,并且很好地抑制边缘细节的扭曲(表 1).
表 1-表 3给出了多个噪声标准偏差情况下,不同去噪方法的PSNR,SSIM,VIF方面的比较结果,该结果是不同算法利用数据集Set12中12张灰度图进行测试的平均值.从表 1,表 2,表 3中可以看出,在不同的噪声标准偏差情况下,本文方法在PSNR,SSIM,VIF指标上比其他去噪方法表现更好,明显地体现出本文方法在去噪方面的优越性.
3.1. 评价指标
3.2. 实验结果分析
-
本文提出一种结合Curvelet变换与加权双边滤波的图像去噪方法,该方法采用加权双边滤波法去除图像中的噪声,然后通过Curvelet变换很好地保留了图像的边缘信息和纹理细节,在图像中恢复这些细节不仅可以提高图像质量,还可以引发用户对图像纹理细节更深层次的理解.通过与其他一些先进图像去噪方法的对比实验可以看出,本文算法在PSNR,VIF和SSIM方面均优于其他算法,并且在有效去除图像噪声的同时,对图像中的纹理和伪像进行了细化.因此,本文方法可以用于诸如医学成像领域,专门增强超声和磁共振图像中的图像质量.



 下载:
下载: