高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

基于鲁棒自适应归一化卷积的遥感图像融合算法

, 

上一篇

下一篇

郭玥, 朱齐亮. 基于鲁棒自适应归一化卷积的遥感图像融合算法[J]. 西南师范大学学报(自然科学版), 2021, 46(1): 13-18. doi: 10.13718/j.cnki.xsxb.2021.01.003
引用本文: 郭玥, 朱齐亮. 基于鲁棒自适应归一化卷积的遥感图像融合算法[J]. 西南师范大学学报(自然科学版), 2021, 46(1): 13-18. doi: 10.13718/j.cnki.xsxb.2021.01.003
shu
GUO Yue, ZHU Qi-liang. Remote Sensing Image Fusion Algorithm Based on Robust Adaptive Normalized Convolution[J]. Journal of Southwest China Normal University(Natural Science Edition), 2021, 46(1): 13-18. doi: 10.13718/j.cnki.xsxb.2021.01.003
Citation: GUO Yue, ZHU Qi-liang. Remote Sensing Image Fusion Algorithm Based on Robust Adaptive Normalized Convolution[J]. Journal of Southwest China Normal University(Natural Science Edition), 2021, 46(1): 13-18. doi: 10.13718/j.cnki.xsxb.2021.01.003
shu

基于鲁棒自适应归一化卷积的遥感图像融合算法

  • 1.

    山西工商学院 计算机信息工程学院，太原 030006

  • 2.

    华北水利水电大学 信息工程学院，郑州 400045

  • 基金项目: 山西省教育厅教育科学“十三五”规划项目(GH-16166)
详细信息
    作者简介:

    郭玥，讲师，主要从事计算机应用研究 .

  • 中图分类号: TP393

Remote Sensing Image Fusion Algorithm Based on Robust Adaptive Normalized Convolution

  • 1.

    College of Computer Information Engineering, Shanxi Technology and Business College, Taiyuan 030006, China

  • 2.

    School of Information Engineering, North China University of Water Resources and Hydropower, Zhengzhou 400045, China

  • 摘要: 针对当前遥感图像融合中容易出现光谱信息失真和边缘细节丢失的问题，提出一种基于鲁棒自适应归一化卷积的全色与多光谱图像融合算法.该方法基于归一化卷积思想，利用投影到子空间的局部信号逼近技术对不规则采样数据进行高分辨率图像重建，自适应归一化卷积中使用的窗函数通过对更多相同意义的样本进行分组，有助于改进分析和提高信噪比，减少不连续面的扩散.实验结果表明，相对于其他优秀融合方法，本文方法更具优势，能够更好地重建光谱信息和保留边缘细节.
    Abstract: Aiming at the problems of spectral information distortion and edge detail loss in remote sensing image fusion, a fusion algorithm of panchromatic and multi-spectral image based on robust adaptive normalized convolution has been proposed. This method is based on the idea of normalized convolution, by which to use local signal approximation technology projected into the subspace to reconstruct high-resolution images of irregularly sampled data. The window function used in adaptive normalized convolution has the same meaning for more grouping of samples helps to improve the analysis and signal-to-noise ratio and reduce the dispersion of discontinuous surfaces. Experimental results show that compared with other excellent fusion methods, the proposed method has more advantages, and can better reconstruct spectral information and retain edge details.
  • 加载中

  • 图 1  提出的融合算法流程图

    下载: 全尺寸图片 幻灯片

    图 2  不同算法在worldwiew-2遥感图像的融合结果

    下载: 全尺寸图片 幻灯片

    表 1  worldwiew-2遥感图像的定量结果

    方法 RMSE RASE NAE LMSE
    HIS_HW 18.08 33.56 0.22 0.47
    NSCT 17.89 33.09 0.21 0.43
    MSVD 19.03 35.11 0.24 0.51
    本文方法 17.59 32.78 0.20 0.41
    下载: 导出CSV
  • [1] KULKARNI J S, BICHKAR R S. Comparative Analysis of Image Fusion Using DCT, DST, DWT, Walsh Transform and Kekre's Wavelet Transform[M]//Advances in Intelligent Systems and Computing. Singapore: Springer Singapore, 2017.
    [2] RESTAINO R, VIVONE G, DALLA MURA M, et al. Fusion of Multispectral and Panchromatic Images Based on Morphological Operators[J]. IEEE Transactions on Image Processing, 2016, 25(6): 2882-2895. doi: 10.1109/TIP.2016.2556944
    [3] HE G Q, XING S Y, XIA Z Q, et al. Panchromatic and Multi-spectral Image Fusion for New Satellites Based on Multi-channel Deep Model[J]. Machine Vision and Applications, 2018, 29(6): 933-946. doi: 10.1007/s00138-018-0964-5
    [4] 焦姣, 吴玲达, 于少波, 等.混合多尺度分析和改进PCNN相结合的图像融合方法[J].计算机辅助设计与图形学学报, 2019, 31(6): 988-996.
    [5] 李旭, 高雅楠, YUE S G.一种尺度感知型遥感图像融合新方法[J].宇航学报, 2017, 38(12): 1348-1353.
    [6] HAMED A A, AL-SAFAR A, TAHA N A. Panchromatic and Multispectral Image Fusion by Combining IHS Transform and Haar Wavelet[J]. Ibn AL- Haitham Journal for Pure and Applied Science, 2017, 30(3): 236-242. doi: 10.30526/30.3.1624
    [7] LIU J H, ZHANG J, DU Y F. A Fusion Method of Multi-spectral Image and Panchromatic Image Based on NSCT Transform and Adaptive Gamma Correction[C]//2018 3rd International Conference on Information Systems Engineering (ICISE). Shanghai: IEEE, 2018.
    [8] GHARBIA R, HASSANIEN A E, EL-BAZ A H, et al. Multi-spectral and Panchromatic Image Fusion Approach Using Stationary Wavelet Transform and Swarm Flower Pollination Optimization for Remote Sensing Applications[J]. Future Generation Computer Systems, 2018, 88: 501-511. doi: 10.1016/j.future.2018.06.022
    [9] LI F L, HONG S H, WANG L. A New Satellite Image Fusion Method Based on Distributed Compressed Sensing[C]//2018 25th IEEE International Conference on Image Processing (ICIP). Athens: IEEE, 2018.
    [10] HE G Q, XING S Y, DONG D D, et al. Panchromatic and multi-spectral image fusion method based on two-step sparse representation and wavelet transform[C]//2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC). Kuala Lumpur: IEEE, 2017.
    [11] RAKSHIT R D, NATH S C, KISKU D R. Face Identification Using some Novel Local Descriptors under the Influence of Facial Complexities[J]. Expert Systems with Applications, 2018, 92: 82-94. doi: 10.1016/j.eswa.2017.09.038
    [12] ZUO B X, HU X Y, LIU S, et al. Delineation of Overlapping Magnetic Field Source Boundaries with a 3-D Multi-layer Convolution Model[J]. Journal of Applied Geophysics, 2018, 150: 74-83. doi: 10.1016/j.jappgeo.2018.01.010
    [13] Priya G P, Venkateswarlu T. An Improved Image Contrast Enhancement Using Multi Resolution Singular Value Decomposition[J]. International Journal of Applied Engineering Research, 2017, 12(18): 7215-7218.
    [14] ZANNI S, DE ROSA A. Remote Sensing Analyses on Sentinel-2 Images: Looking for Roman Roads in Srem Region (Serbia)[J]. Geosciences, 2019, 9(1): 25-43. doi: 10.3390/geosciences9010025
    [15] SUNDAR K J A, JAHNAVI M, LAKSHMISARIT K. Multi-sensor Image Fusion Based on Empirical Wavelet Transform[C]//2017 International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT). Tamil Nadu: IEEE, 2017.
  • 加载中
图( 2) 表( 1)
计量
  • 文章访问数:  1434
  • HTML全文浏览数:  1434
  • PDF下载数:  80
  • 施引文献:  0
出版历程
  • 收稿日期:  2020-02-03
  • 刊出日期:  2021-01-20

基于鲁棒自适应归一化卷积的遥感图像融合算法

    作者简介: 郭玥，讲师，主要从事计算机应用研究
  • 1. 山西工商学院 计算机信息工程学院，太原 030006
  • 2. 华北水利水电大学 信息工程学院，郑州 400045
  • 收稿日期:  2020-02-03
基金项目:  山西省教育厅教育科学“十三五”规划项目(GH-16166)

摘要: 针对当前遥感图像融合中容易出现光谱信息失真和边缘细节丢失的问题，提出一种基于鲁棒自适应归一化卷积的全色与多光谱图像融合算法.该方法基于归一化卷积思想，利用投影到子空间的局部信号逼近技术对不规则采样数据进行高分辨率图像重建，自适应归一化卷积中使用的窗函数通过对更多相同意义的样本进行分组，有助于改进分析和提高信噪比，减少不连续面的扩散.实验结果表明，相对于其他优秀融合方法，本文方法更具优势，能够更好地重建光谱信息和保留边缘细节.

English Abstract

    全文HTML

  • 遥感图像分为高空间分辨率全色图像(panchromatic image，PAN)和高光谱分辨率多光谱图像(multi-spectral image，MS)[1].由于现有技术的局限，遥感卫星很难同时获取具备高空间分辨率和高光谱分辨率的遥感图像.在图像处理中，将具有良好光谱信息的多光谱图像与具有良好空间信息的全色图像进行融合，可以有效提高遥感图像质量[2-3].

    为了满足众多领域对高分辨率和高空间率遥感图像的需求，研究人员已经提出许多遥感图像融合方法，主要分为3种：成分替代方法、多分辨率分析方法和基于物理模型方法[4].成分替代方法是将多光谱图像变换到空间成分与光谱成分分离的新空间上，利用经过处理的全色图像对空间成分进行增强，然后经过逆变换得出具有高空间分辨率的多光谱图像.最广泛使用的成份替代方法主要是主成分分析(principal component analysis，PCA)[5]和IHS(亮度Intensity、色调Hue、饱和度Saturation)方法[6]等，这些方法操作简单，可以有效地消除部分冗余，但是存在容易产生光谱扭曲，空间分辨率不高的问题.多分辨率分析方法采用多尺度分解方式，对目标图像进行多分辨率分解，将提取到的全色图像中的高频信息及相关细节注入多光谱图像.最常用的多分辨率分析方法如非下采样Contourlet变换[7]、小波变换[8]等在融合时会引入较多的人为噪声.基于物理模型的融合方法是根据物理模型采用不同技术手段对低分辨率的多光谱图像进行修复，从而获得具有高分辨率的多光谱图像.该类方法的主要代表为基于压缩感知技术[9]和稀疏表示[10]的融合方法，能够在一定程度上提高遥感图像的融合效果，但是也存在细节丢失的问题.

    目前，大多数遥感图像的融合方法都存在图像光谱失真和边缘细节丢失的现象，只是在失真量上有所不同而已.针对上述问题，本文提出一种基于鲁棒自适应归一化卷积的全色与多光谱图像融合算法，该算法在小面模型(Facet Model)中引入基于归一化卷积的结构自适应函数，提高有效样品的可信度，减少边缘模糊和细节丢失现象的发生.

1.   归一化卷积

    1.1.   小面模型

  • 小面模型(Facet Model)原理是假设将一幅图像划分为若干个连接的区域，满足一定形状限制和灰度分布的单个区域定义为一个Facet[11].灰度分布要求每个Facet的灰度函数是其对应区域内像元行与列的多项式函数，因此可以使用若干个相互连接的Facet来近似一幅图像. Facet模型可以根据灰度函数次数的不同，分为平面或斜面模型，二次或三次模型等.一个二维Facet模型可以通过二元三次多项式逼近二维像素邻域中的灰度值.

    式(1)中：r和c表示局部图像的像素坐标，ki表示拟合系数.

    • 1.2.   标准归一化卷积

  • 归一化卷积[12]是一种依赖于信号模型及其可信度的技术，可以定义为一种利用一组基函数的投影对信号进行建模的方法.考虑基本多项式基：{1，p，q，p2，q2，pq，…}，其中1=[1，1，…，1]T，p=[p1，p2，…，pN]T，q=[q1，q2，…，qN]T，p2=[p12，p22，…，pN2]T由N个输入样本的局部坐标构成.将此多项式基函数用于归一化卷积，使其与泰勒级数展开式相似.再聚焦于a0={p0，q0}的局部邻域内，通过多项式估计a={p+p0，q+q0}位置的强度值.

    式(2)中：局部坐标是相对于中心点a0的N个样本的{p，q}. m0(a0)=[m0，m1，…，mn]T(a0)是投影系数.在小面模型中对所有邻域样本按相同比例应用权重，而归一化卷积则采用一个可使多项式拟合局部化的适用函数.适用函数m0(a0)一般为高斯函数，其大小与分析尺度相当.在正则化卷积中使用的每个输入信号都允许有自己的确定值.

    根据应用类型和处理速度的需要，可以选择多项式的阶数.复杂结构在更高阶的归一化卷积下得到拟合，从而在计算量上得到折衷.由于高阶比原始信号更适合噪声，通常选择一阶归一化卷积.插值的质量也取决于适用函数的规模.为了实现平衡的局部分析，适用性函数必须足够大，以包含足够数量的样本.插值结果应具有最小的模糊性和覆盖大样本，一般采用高斯适用函数实现该目的.

    为了求解a0位置处的投影系数，将在以a0为中心的适用函数s上逼近近似误差.

    式(3)中：信号0≤c(a)≤1的可信度表示在a处测量的信任值，0表示不可靠数据，1表示可靠数据.在包含N个样本的邻域中，最小二乘回归解的矩阵形式为

    式(4)中：M是具有输入强度f(a)的q×1矩阵，X=[x1，x2，…，xp]表示在输入的N个采样点处基函数p的q×p矩阵. W=diag(s)·diag(c)是一个q×q对角矩阵，由函数s与信号可信度的乘积生成.

    在定期采样数据和固定适用性函数的情况下，可以通过使用卷积运算来实现归一化卷积.使用卷积后式(4)可以简化为

    式(5)中：$\hat f $表示插值图像，c·f是图像可信度和强度值的逐像素乘积，⊗是卷积算符.一阶归一化卷积需要9次卷积，并且生成3个图像，分别为插值图像$\hat f $1，$\hat f $p，$\hat f $q，并由以下方程给出.

    式(6)中：p，q，p2，pq以及q2被称为二维基函数的核.信号可信度值中的非均匀性可以通过使用归一化项进行校正，归一化项是式(5)中的分母项和式(6)中的逆元项，即为归一化卷积.

2.   基于鲁棒自适应归一化卷积的融合算法

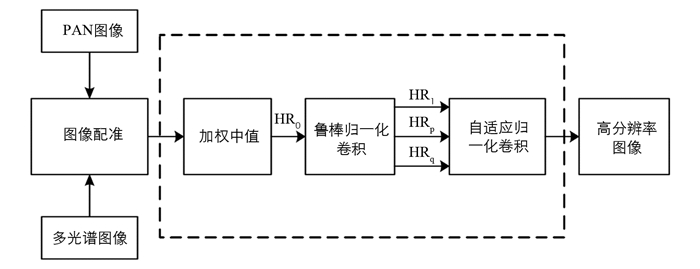
  • 本文采用两步高分辨率方法，如图 1所示.第一步执行图像配准过程，使用梯度移位估计器将全色图像和多光谱图像对齐到公共帧，以达到亚像素的精度.第二步是融合过程，包括3个中间阶段，即加权中值、稳健归一化卷积和自适应归一化卷积.中值滤波器构造鲁棒归一化卷积所需的第一估计HR0.鲁棒归一化卷积使用该估计值，并生成高分辨率图像的改进估计HR1以及2个指令HRp和HRq.自适应归一化卷积利用p和q方向的指令构造适用函数.

    在归一化卷积的情况下，信号的可信度需要预先知道.因此，在a0位置展开多项式之前引入邻域像素光度加权方案[12]，保证邻域获得可信度.此处的可信度是残差f－$\hat f $的高斯函数，并通过分配低权重来消除之间的异常值.

    式(7)中：f(a)和$\hat f $(a，a0)是测量和估计的强度，强度估计是利用s0中心处多项式展开进行的. $\hat f $(a，a0)的适宜范围由光束扩散σr决定，当残差小于σr时，样品的可信度接近1，而残差大于2×σr的样品可信度很低.

    局部平面的一阶二维归一化卷积至少需要3个样本.在一般情况下，由于邻域是局部算子，所以需要对其进行运算.当样本数足够时，适用函数的尺度很小.因此，需要一个锐化重建过程.在输入样本数不足的情况下，应使适用函数更大，以容纳足够的样本，实现稳定的多项式拟合.因此，本文提出了一种针对边缘增强融合过程的自适应适用函数，该函数可为小细节感知的应用提供清晰的图像.

    本文提出的自适应适用性函数是高斯函数，通过适当改变主轴来调节局部有效方向.

    式(8)中：a0={p0，q0}为中心点，根据局部尺度σc，适用函数s通过调整自身大小来收集足够数量的样本. σu和σv是关于局部尺度σc定义的有向高斯核，其定义为

    式(9)、式(10)中：自适应参数σ>0，作为适用函数偏心率的上限.当A=1/2时，本文认为最大偏心距的自适应参数σ=1/2.选择A=1/2的原因，是在鲁棒归一化卷积之后进行了第二次归一化卷积.

3.   实验结果与分析

  • 本文所有实验在一台配置为Intel Xeon E5-2698 (20-Core) CPU @2.20 GHz和NVIDIA Tesla V100 4×16 GB GPU的NVIDIA DGX工作站上进行.采用图 2图像进行自适应归一化卷积融合实验，并将其与色调饱和和Haar变换联合方法(IHS_HW)[6]、非下采样Contourlet变换(NSCT)[7]以及多分辨率奇异值分解方法(MSVD)[13]的实验结果进行对比.

    图 2实验图像的具体参数[14]为：由卫星worldwiew-2拍摄的一组分辨率分别为2 m和50 cm的多光谱图像和全色图像.在测试过程中，鲁棒归一化卷积的适用性函数范围固定在σu=σv=1，光度扩展设置为16位输入图像范围的1%(σr=500).为了更好地评价去雾算法的性能，本文从定性和定量2个方面进行评估.

    • 3.1.   定性分析

  • 图 2给出了不同融合算法在实验图像中的测试结果.从图 2中可以看出，本文的鲁棒自适应归一化卷积方法具有较高的细节层次.定量分析结果表明，自适应归一化卷积方法在重建质量和纹理细节方面更优于其他方法.

    • 3.2.   定量分析

  • 为了进一步验证，本文利用均方根误差(RMSE)、拉普拉斯均方误差(LMSE)、归一化绝对误差(NAE)和相对平均光谱误差(RASE)4个评价指标[15]来验证算法的有效性.

    均方根误差(RMSE)是观测值与真值偏差的平方与观测次数n比值的平方根，其值越大说明融合图像越偏离真实值.

    式(11)中：f(xi)和g(xi)分别表示复原图像和原始图像.

    拉普拉斯均方误差(LMSE)表示原始图像与融合图像的局部对比度，其值越大，图像的降质越大.

    式(12)中：

    归一化绝对误差(NAE)将融合图像的平均绝对误差对原始图像的均值归一化，其值越低，说明融合图像效果越好，该度量定义为

    相对平均光谱误差(RASE)是衡量融合图像光谱质量的一种度量，其值越低，说明融合图像的光谱质量越高，定义为

    式(14)中：M表示原始多光谱图像N个光谱波段的平均辐射值，xi(i=1，2，3)分别对应R，G，B波段.

    表 1给出了基于上述参数的现有图像和本文方法图像的定量结果.重建图像的均方根误差、拉普拉斯均方误差、归一化绝对误差和相对平均光谱误差值越小越好.定量性能测量表明，本文的鲁棒自适应归一化卷积方法优于其他现有方法，其误差较小.

4.   结语

  • 本文提出一种基于鲁棒自适应归一化卷积的全色图像与多光谱图像融合方法，解决了遥感图像融合过程中出现的光谱信息失真和边缘细节丢失的问题.具有鲁棒多项式拟合的自适应适用函数是该方法的新颖之处.适用性函数的扩展和收缩特性使其更具优势，并避免了沿直线和边缘的模糊.由于强度分布在局部分析中被充分忽略，有效的样本确定性减少了角点模糊和更精细的细节.实现结果表明，本文的融合算法性能优于其他算法，而且该方法不仅适用于融合过程，还可以推广到图像修复、双边滤波、运动估计等领域.

参考文献 (15)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回