-
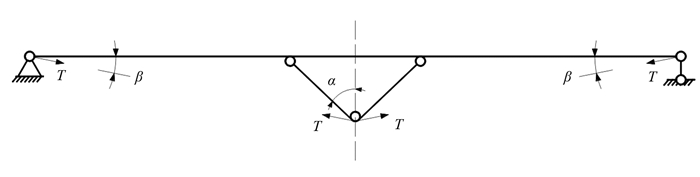
张弦梁结构是由刚性压弯构件上弦(拱)、柔性拉索(钢拉杆)及撑杆组合而成的结构构件,该结构通过撑杆减小梁的弯矩和变形,由索抵消拱端推力,降低对边界条件的要求,从而充分发挥拱结构的受力优势和高强索的抗拉特性[1]. 张弦梁结构最早由日本学者提出,并开展了不同几何参数与力学性能对张弦梁结构整体稳定性能影响的分析[2]. 陆伟等[3]则对索拱结构与张弦梁进行了研究,对比分析了索拱结构及张弦梁性能与其矢高的关系. 随着研究的深入,不同形式的张弦梁结构也得到进一步的研究和应用,董石麟[4]阐述了我国预应力大跨度空间钢结构应用与发展的基本情况. 然而,上述针对张弦梁结构的研究大多集中在撑杆采用单根或多根竖向布置的形式,本文则以采用撑杆斜向布置的预应力张弦梁为研究对象,基于理论推导和数值分析的手段对其稳定性能展开研究,如图 1所示.
全文HTML
-
本文研究的斜撑杆张弦梁如图 1(c)所示,在自重和拉索预应力作用下斜撑杆张弦梁跨中截面分别为下部受拉和上部受压,为了抵消斜撑杆张弦梁在自重作用下的跨中弯矩,可以通过调整拉索预应力的方式完成. 为此,本文在确定拉索预应力大小时即是按照斜撑杆张弦梁在自重和拉索预应力作用下跨中截面弯矩大小相等的原则进行. 在推导自重作用下的跨中弯矩时,可将横梁自重等效为作用在张弦梁上的满跨均布荷载,撑杆自重可以等效为作用在张弦梁上的集中荷载,如图 2所示,其中q为横梁自重引起的均布荷载; Q为撑杆的自重.
根据结构力学知识,可以推得其跨中弯矩为
式中M1为自重工况下的最大跨中弯矩; l为梁的长度; a为撑杆端点距离梁的垂距; α为撑杆和梁中点法线的夹角.
在拉索初始预张力作用下张弦梁的受力分析如图 3所示,其中T为拉索中的预拉力.
利用结构力学知识并结合图 3,可以推得斜撑杆张弦梁在拉索预应力作用下的跨中弯矩为
式中M2为预应力工况下的最大跨中弯矩; β为拉索与梁的夹角.
根据前述自重和初始预应力产生的跨中弯矩数值相等的原则,有:
由式(1)、(2)、(3)有:
-
本文的数值分析采用有限元软件ABAQUS完成,其中撑杆和横梁采用梁单元模拟,单元类型为B31; 而预应力索采用桁架单元模拟,其单元类型为T3D2[5]. 在分析时,横梁的长度为4 800 mm,考虑撑杆倾角为15°,30°,45°和60°,矢高为240,360,480,600 mm. 考虑的荷载情况为集中荷载,施加在横跨梁中. 横梁和撑杆的材料均采用Q345钢,其弹性模量为201 000 N/mm2,采用理想弹塑性模型; 拉索采用强度为1 470 MPa的钢绞线,其弹性模量为160 000 N/mm2,索径ϕ分别为12,14,16,18,20,22 mm[6]. 为了准确反映斜撑杆张弦梁的稳定性能,本文对其进行了非线性屈曲分析,分析时初始缺陷按照最低阶线性屈曲模态施加,缺陷大小取为l/300(l为横梁长度)[7].
1.1. 拉索初始预应力
1.2. 有限元分析方法
-
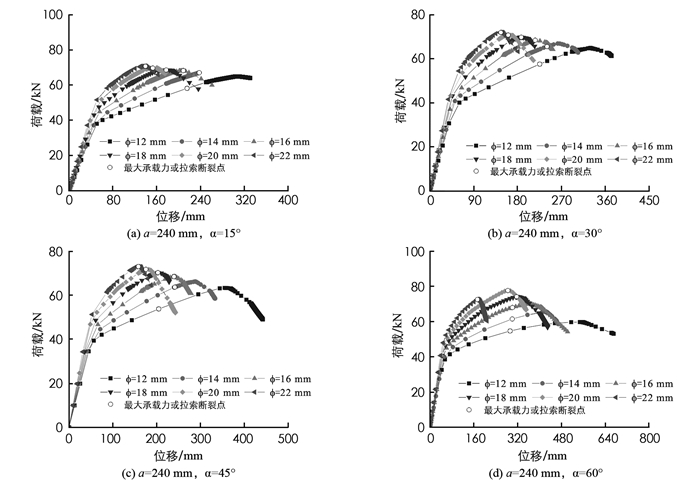
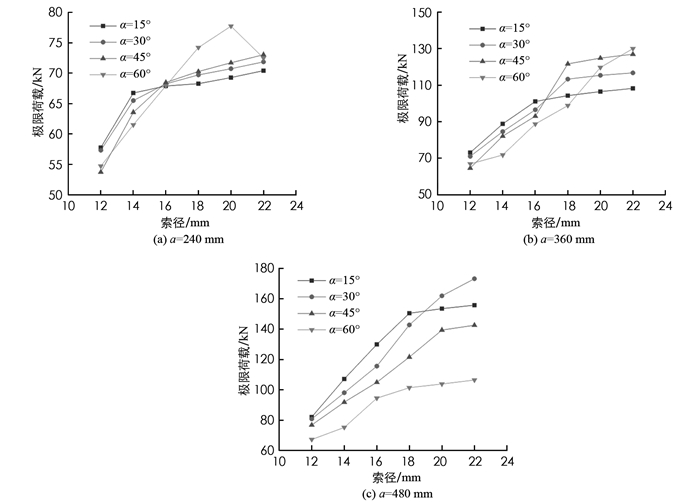
通过非线性屈曲分析,本文考察了拉索直径对斜撑杆张弦梁稳定性能的影响,分析结果如图 4和图 5所示,图中横轴的位移表示张弦梁跨中挠度. 在本文的荷载-位移曲线中,以空心圆圈表示张弦梁达到了最大承载能力或者拉索发生了破坏. 可以看出,无论矢高(a)为240,360,480 mm,结构稳定性能均随拉索直径呈现出类似的变化规律,即增大拉索直径可以提高结构最大承载能力和刚度. 对于撑杆角度而言,当撑杆角度增大时,小索径结构的最大承载能力随之减小,而大索径结构的最大承载力会随之增大.
-
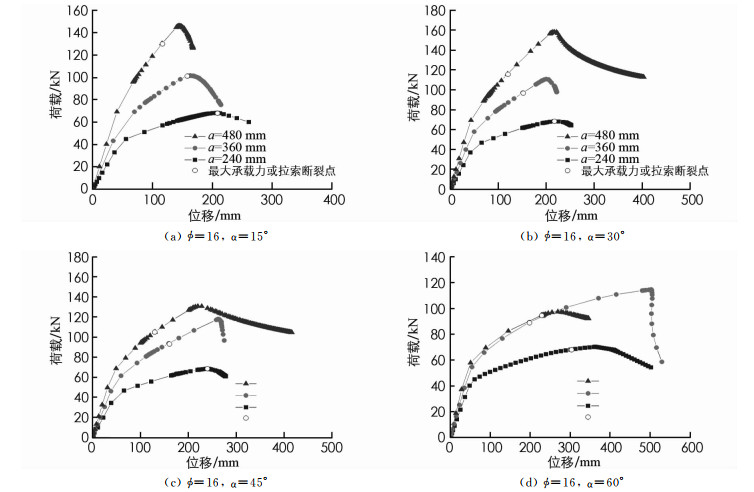
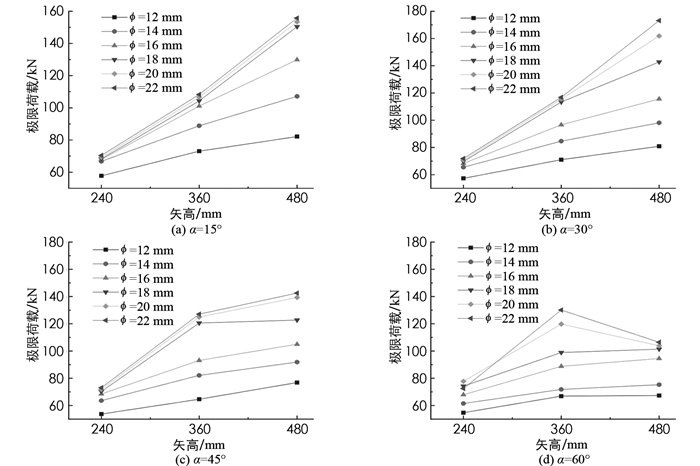
与上一节的方法类似,本节重点考察了矢高对斜撑杆张弦梁稳定性能的影响. 分析结果如图 6和图 7所示,图中横轴的位移表示张弦梁跨中挠度. 可以看出,随着矢高(a)的增加,斜撑杆张弦梁的承载能力和刚度均会明显提升. 由图 6(d)和图 7(d)可以看出,当撑杆夹角过大和长度过长时,其承载能力反而会降低,因为此时对应的撑杆长度较长,撑杆会率先失稳.
2.1. 拉索直径的影响
2.2. 矢高的影响
-
本文通过建立预应力斜撑杆张弦梁模型对其预应力的确定原则及影响结构极限承载能力的因素进行了分析,结论总结如下:
1) 针对斜撑杆张弦梁的特性提出了拉索初始预应力的设计方法,即令预应力与自重产生的跨中截面弯矩相等,基于这个原则推导了初始预应力的计算公式.
2) 对于撑杆布置方式为斜撑杆布置的张弦梁而言,拉索索径与矢高的增大可以有效提升这类结构构件的最大承载力和刚度; 当撑杆角度增大时,小索径结构的最大承载能力会随之减小,大索径结构的最大承载力会增大; 而当结构矢高、撑杆角度均过大时,结构构件会发生撑杆失稳的现象,对结构承载能力产生负面的影响.




 下载:
下载: