高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

基于改进人工蜂群算法的大数据优化

, 

上一篇

下一篇

南楠, 严英占. 基于改进人工蜂群算法的大数据优化[J]. 西南师范大学学报(自然科学版), 2021, 46(3): 20-26. doi: 10.13718/j.cnki.xsxb.2021.03.004
引用本文: 南楠, 严英占. 基于改进人工蜂群算法的大数据优化[J]. 西南师范大学学报(自然科学版), 2021, 46(3): 20-26. doi: 10.13718/j.cnki.xsxb.2021.03.004
shu
NAN Nan, YAN Ying-zhan. Big Data Optimization Based on Improved Artificial Bee Colony Algorithm[J]. Journal of Southwest China Normal University(Natural Science Edition), 2021, 46(3): 20-26. doi: 10.13718/j.cnki.xsxb.2021.03.004
Citation: NAN Nan, YAN Ying-zhan. Big Data Optimization Based on Improved Artificial Bee Colony Algorithm[J]. Journal of Southwest China Normal University(Natural Science Edition), 2021, 46(3): 20-26. doi: 10.13718/j.cnki.xsxb.2021.03.004
shu

基于改进人工蜂群算法的大数据优化

  • 1.

    岭南师范学院基础教育学院，广东 湛江 524048

  • 2.

    中国电子科技集团第54研究所，石家庄 050081

详细信息
    作者简介:

    南楠, 硕士, 讲师, 主要从事计算机应用研究 .

  • 中图分类号: TP391

Big Data Optimization Based on Improved Artificial Bee Colony Algorithm

  • 1.

    Basic Education College, Lingnan Normal University, Zhanjiang Guangdong 524048, China

  • 2.

    China Electronics Technology Group 54th Institute, Shijiazhuang 050081, China

  • 摘要: 针对传统方法无法解决具有5 V独特属性的大数据优化问题, 提出基于改进人工蜂群(Artificial Bee Colony, ABC)算法的大数据优化信号重构算法.该算法通过引导所考虑问题的现有信息来初始化食物源, 在引领蜂阶段使用交叉和变异算子生成候选解, 并使用轮盘赌反向选择机制生成要交叉的食物源, 观察蜂采用Rechenberg 1/5变异规则来自适应地控制扰动大小, 在全局最优解的邻域内提供固定的搜索操作.实验结果表明: 与其他方法相比, 本文算法具有更稳健的最优和平均最优目标函数值, 对大数据优化问题能够产生令人满意的结果.
    Abstract: To solve the problem of traditional methods without solving the big data optimization problem with 5 V unique attributes, an improved artificial bee colony(ABC) algorithm has been proposed to optimize the big data signal reconstruction algorithm. The algorithm initializes the food source by guiding the existing information of the problem under consideration, then uses the crossover and mutation operators to generate candidate solutions in the leading bee stage, and uses the roulette selection mechanism to generate the food sources to be crossed. Finally, the bee adopts Rechenberg 1/5 mutation rule to adaptively control the size of the perturbation, and provide a fixed search operation in the neighborhood of the global optimal solution. The experimental results show that compared with other methods, the proposed algorithm has more robust optimal and average optimal objective function values, which can produce satisfactory results for big data optimization problems.
  • 加载中

  • 图 1  改进ABC算法流程图

    下载: 全尺寸图片 幻灯片

    表 1  将各算法进行1 000个周期的比较

    算法 标准ABC算法 交叉ABC算法 本文算法
    D4 平均 1.67e+01 6.24e+00 6.13e-02
    最佳 1.57e+01 5.87e+00 6.13e-02
    D4N 平均 1.66e+01 6.13e+00 5.92e-02
    最佳 1.59e+01 5.46e+00 5.92e-02
    D12 平均 2.06e+01 1.58e+01 1.94e-03
    最佳 2.02e+01 1.53e+01 1.94e-03
    D12N 平均 2.06e+01 1.57e+01 1.83e-03
    最佳 2.01e+01 1.54e+01 1.83e-03
    D19 平均 2.15e+01 1.82e+01 2.55e-03
    最佳 2.12e+01 1.78e+01 2.54e-03
    D19N 平均 2.14e+01 1.82e+01 2.60e-03
    最佳 2.07e+01 1.80e+01 2.59e-03
    下载: 导出CSV

    表 2  将各算法进行1 000个周期的比较

    算法 DA HDE 本文算法
    D4 平均 4.27e+00 6.54e-02 6.13e-02
    最佳 3.72e+00 6.32e-02 6.13e-02
    D4N 平均 4.46e+00 7.87e-02 5.92e-02
    最佳 3.81e+00 6.01e-02 5.92e-02
    D12 平均 4.48e+00 5.78e-02 1.94e-03
    最佳 3.91e+00 1.98e-03 1.94e-03
    D12N 平均 4.43e+00 1.21e-02 1.83e-03
    最佳 3.98e+00 3.41e-03 1.83e-03
    D19 平均 4.53e+00 1.06e-01 2.55e-03
    最佳 4.02e+00 1.02e-02 2.54e-03
    D19N 平均 4.53e+00 5.76e-02 2.60e-03
    最佳 4.13e+00 2.12e-02 2.59e-03
    下载: 导出CSV
  • [1] WANG Y C, KUNG L, BYRD T A. Big Data Analytics: Understanding Its Capabilities and Potential Benefits for Healthcare Organizations[J]. Technological Forecasting and Social Change, 2018, 126(1): 3-13.
    [2] BEAM A L, KOHANE I S. Big Data and Machine Learning in Health Care[J]. JAMA, 2018, 319(13): 1317-1318. doi: 10.1001/jama.2017.18391
    [3] KONG F S, LIN X L. The Method and Application of Big Data Mining for Mobile Trajectory of Taxi Based on MapReduce[J]. Cluster Computing, 2019, 22(5): 11435-11442.
    [4] OUSSOUS A, BENJELLOUN F Z, AIT LAHCEN A, et al. Big Data Technologies: a Survey[J]. Journal of King Saud University-Computer and Information Sciences, 2018, 30(4): 431-448. doi: 10.1016/j.jksuci.2017.06.001
    [5] ROY C, RAUTARAY S S, PANDEY M. Big Data Optimization Techniques: A Survey[J]. International Journal of Information Engineering & Electronic Business, 2018, 10(4): 41-48.
    [6] WU C R, ZAPEVALOVA E, CHEN Y, et al. Time Optimization of Multiple Knowledge Transfers in the Big Data Environment[J]. Computers, Materials & Continua, 2018, 54(3): 269-285.
    [7] 王小君. 基于人工蜂群算法的数据分类感知研究[J]. 计算机与数字工程, 2018, 46(5): 866-869, 915. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-JSSG201805004.htm
    [8] CAO Y C, LU Y, PAN X Q, et al. An Improved Global Best Guided Artificial Bee Colony Algorithm for Continuous Optimization Problems[J]. Cluster Computing, 2019, 22(2): 3011-3019.
    [9] BRAJEVI CI, STANIMIROVI CP S, LI S, et al. A Hybrid Firefly and Multi-Strategy Artificial Bee Colony Algorithm[J]. International Journal of Computational Intelligence Systems, 2020, 13(1): 810-821. doi: 10.2991/ijcis.d.200612.001
    [10] SUN Y, GAO Y L. An Efficient Modified Particle Swarm Optimization Algorithm for Solving Mixed-Integer Nonlinear Programming Problems[J]. International Journal of Computational Intelligence Systems, 2019, 12(2): 530-543. doi: 10.2991/ijcis.d.190402.001
    [11] SHUKLA S, JAIN M. A Novel System for Effective Speech Recognition Based on Artificial Neural Network and Opposition Artificial Bee Colony Algorithm[J]. International Journal of Speech Technology, 2019, 22(4): 959-969. doi: 10.1007/s10772-019-09639-0
    [12] WANG H, ZHOU X Y, SUN H, et al. Firefly Algorithm with Adaptive Control Parameters[J]. Soft Computing, 2017, 21(17): 5091-5102. doi: 10.1007/s00500-016-2104-3
    [13] YI J H, DEB S, DONG J Y, et al. An Improved NSGA-III Algorithm with Adaptive Mutation Operator for Big Data Optimization Problems[J]. Future Generation Computer Systems, 2018, 88(11): 571-585.
    [14] MAFARJA M, ALJARAH I, HEIDARI A A, et al. Binary Dragonfly Optimization for Feature Selection Using TimeVarying Transfer Functions[J]. Knowledge-Based Systems, 2018, 161(12): 185-204.
    [15] KARABOGA D, KAYA E. Training ANFIS by Using an Adaptive and Hybrid Artificial Bee Colony Algorithm(aABC)for the Identification of Nonlinear Static Systems[J]. Arabian Journal for Science and Engineering, 2019, 44(4): 3531-3547. doi: 10.1007/s13369-018-3562-y
    [16] EL MAJDOULI M A, RBOUH I, BOUGRINE S, et al. Fireworks Algorithm Framework for Big Data Optimization[J]. Memetic Computing, 2016, 8(4): 333-347. doi: 10.1007/s12293-016-0201-6
  • 加载中
图( 1) 表( 2)
计量
  • 文章访问数:  978
  • HTML全文浏览数:  978
  • PDF下载数:  69
  • 施引文献:  0
出版历程
  • 收稿日期:  2020-02-27
  • 刊出日期:  2021-03-20

基于改进人工蜂群算法的大数据优化

    作者简介: 南楠, 硕士, 讲师, 主要从事计算机应用研究
  • 1. 岭南师范学院基础教育学院，广东 湛江 524048
  • 2. 中国电子科技集团第54研究所，石家庄 050081
  • 收稿日期:  2020-02-27

摘要: 针对传统方法无法解决具有5 V独特属性的大数据优化问题, 提出基于改进人工蜂群(Artificial Bee Colony, ABC)算法的大数据优化信号重构算法.该算法通过引导所考虑问题的现有信息来初始化食物源, 在引领蜂阶段使用交叉和变异算子生成候选解, 并使用轮盘赌反向选择机制生成要交叉的食物源, 观察蜂采用Rechenberg 1/5变异规则来自适应地控制扰动大小, 在全局最优解的邻域内提供固定的搜索操作.实验结果表明: 与其他方法相比, 本文算法具有更稳健的最优和平均最优目标函数值, 对大数据优化问题能够产生令人满意的结果.

English Abstract

    全文HTML

  • 无处不在的互联网和移动设备的激增带来了大数据时代个人数据的指数级增长[1, 2], 大数据具有大容量、高速度、多样性、低价值密度和真实性5 V特征[3-4]. 大数据的存在对现实世界优化问题的定义、复杂性和未来发展方向有着不可忽视的影响. 大数据优化问题包含大量的决策变量、目标函数或具有不同数学性质的函数，有时需要实时求解[5]. 传统的数据密集型优化问题已无法应用于大数据优化，迫切需要分析现有技术的性能，确定它们可能存在的缺陷[6], 并考虑与大数据相关的独特属性来探索新的方法.

    人工蜂群(Artificial Bee Colony, ABC)算法是受实际蜜蜂巧妙觅食行为启发而形成的一种最成功的基于群体智能的优化算法[7-8]. ABC算法通过模拟实际蜜蜂的智能食物源搜索、消费和通信行为将人工蜂群分为引领蜂、侦察蜂和观察蜂3类[9]. 引领蜂储存某个食物源的相关信息(蜂窝的距离、方向、食物源的质量等), 并将信息与其他蜜蜂分享[10]. 观察蜂守候在蜂窝里并与各种引领蜂分享相关信息，选择优质食物来源进行搜索. 侦察蜂不使用引领蜂提供的任何信息，而是随机飞行搜索蜂巢附近的新食物源. 由于ABC算法定义良好的蜂蜜阶段、平衡的局部和全局搜索机制、较少的控制参数，已成功用于解决不同工程或实际优化问题[11].

    近年来，有关大数据优化的研究已取得若干成果. 文献[12]提出用于大数据优化的混合多目标萤火虫算法(Firefly Algorithm, FA), 该算法在搜索过程中自动调整控制参数，并采用交叉策略来保持种群多样性. 文献[13]提出基于自适应变异算子改进NSGA-III算法的大数据优化方法，该方法引入自适应变异算子来增强NSGA-III的性能，开发了3种改进的NSGA-III算法来解决一系列大数据优化问题. 文献[14]提出基于二进制蜻蜓算法的特征选择方法，该方法利用8个传递函数将连续搜索空间映射到离散搜索空间，提出时变的S形和V形传递函数利用阶跃矢量对平衡勘探和开发的影响. 该方法在分类准确性、敏感性、特异性、曲线下面积和选择属性数方面具有较高的性能.

    在研究了现有大数据并优化的基础上，本文提出基于改进人工蜂群算法的大数据优化信号重构算法. 该算法对标准ABC算法的食物源初始化、引领蜂阶段和观察蜂阶段进行重要改进，首先利用元启发式算法生成初始食物源，然后在ABC算法的引领蜂阶段与进化算法的特殊选择、交叉算子和变异算子进行杂交，最后观察蜂采取Rechenberg 1/5变异规则来自适应地控制扰动大小，在全局最优解的邻域内提供固定的搜索操作. 为了探索该算法的求解能力，利用CEC 2015年大数据优化大赛上提出的基于不同信号分解的大数据优化问题进行实验. 实验结果表明相对于其他算法，本文提出的方法具有更稳健的最优和平均最优目标函数值，对测试的大数据优化问题都能产生更好的结果.

1.   基于脑电图信号的大数据问题定义

  • 近年来，引入脑电图(Electro Encephalo Graphic, EEG)信号来处理大数据优化，并利用基于群体智能的进化算法对其进行求解. 根据相互依赖的时间序列数量，将从信号测量获得的数据分成6个不同的问题实例D4, D4N, D12, D12N, D19和D19N, 每个时间序列的长度为256. D4, D12和D19分别有4, 12, 19个相互依赖的时间序列. D4N, D12N和D19N也分别有4, 12, 19个时间序列，但它们会随着添加的额外噪声成分而略有变化.

    引入大数据优化问题的主要目标是将实例分为两个子部分：第一子部分应选择尽可能类似于源以获得所需信息，但第二子部分与伪影或噪声相匹配. 设X为表示转换后问题实例的N×M维矩阵，N为时间序列的数量，M为时间序列的长度. S是与X维数相同的另一个矩阵，A是N×N维平方变换矩阵. X, S和A矩阵之间的关系为

    如前所述，主要目的是将S矩阵分为两个子矩阵. 设S1和S2是在分解S矩阵后获得的N×M维矩阵，S1用于表示原始S矩阵，S2表示对应原始S矩阵的测量噪声或伪影. S1和S2矩阵相加获得S矩阵，若用A矩阵对S1和S2进行变换后求和，获得X矩阵.

    由于没有直接的方法将S矩阵分成适当的S1和S2子矩阵，使用皮尔逊相关系数来生成S1和S2, 当用C表示并按式(4)计算的皮尔逊相关系数的非对角线元素被试图最小化为零时，C矩阵的对角线元素被试图最大化.

    式(4)中：covar(X, A×S1)为协方差矩阵，var(X)和var(A×S1)是方差矩阵. 假设S1矩阵，并根据式(4)计算矩阵C, 计算S1和S间的相似度，并控制C的最小化-最大化条件. 定义目标函数f1与C矩阵的非对角线元素最小化和对角线元素最大化特性相关，目标函数f2用于评估S1和S之间的相似度.

    由式(5)、式(6)可以看出，应该将f1和f2函数最小化. 如果将f1和f2函数的权重都设置为1, 并尝试最小化(f1+f2), 则可以定义关于大数据优化概念的单目标问题.

2.   人工蜂群算法

  • 标准人工蜂群(Artificial Bee Colony, ABC)算法分为4个部分：初始化食物来源、引领蜂、观察蜂和侦察蜂.

    • 2.1.   初始化食物来源

  • ABC算法通过初始化与搜索空间中可能的解相对应的食物源来求解优化问题. 设xi是第i个食物源，xij是同一食物源的第j个参数，初始化为

    式(7)中：$x_{j}^{\max }$ 和 $x_{j}^{\min }$分别是第j个参数的上限和下限，rand(0, 1)是从0~1范围内均匀分布的数中随机选择的系数.

    • 2.2.   引领蜂和观察蜂阶段

  • 生成初始食物源后，标准ABC算法将每种食物源分配给一只引领蜂，因此引领蜂数量等于食物源数量，引领蜂负责在指定蜜蜂附近寻找新的食物源. ABC算法通过式(8)对引领蜂这类搜索行为进行建模.

    式(8)中vij是候选食物源vi的第j个参数，vi是xi的邻居食物源，其参数只有第j个候选食物源与xi相同. xij, xkj分别是xi和xk食物源的第j个参数，φ是[-1, +1]之间的随机数，j和k是从{1, 2, …, D}和{1, 2, …, SN}集合中随机确定的索引.

    引领蜂在xi和vi食物源之间进行贪婪选择，以决定在后续循环中所使用的食物源. 设obj(x)为同一食物源的目标函数值的最小解，fit(x)是食物源x的适应度，计算如下式所示.

    将xi食物源代入上式计算其适应度fit(xi), 将vi代替xi食物源代入式(9)计算其适应度fit(vi), 若食物源vi的适合度fit(vi)高于食物源xi的适应度fit(xi), 与xi相关的引领蜂离开xi食物源，则通过设置源特定的试验计数器来用vi替换xi解，该计数器显示访问的食物源未改进为零的次数. 若vi的适合度fit(vi)低于xi的适应度fit(xi), 则引领蜂在将其尝试计数器递增1之后仍会储存xi解.

    当所有引领蜂完成搜索工作并返回蜂巢时，它们通过跳舞向观察蜂告知食物源. 食物源质量和观察蜂可选性之间有很强的关系，为了对这种关系进行建模，ABC算法使用式(10)为每种食物源分配选择概率. 由式(4)可以看出，具有较高适合度值的食物源有更高的偏好概率，当观察蜂选择食物来源时，它会继续在所选食物周围搜索候选者.

    • 2.3.   侦察蜂阶段

  • ABC算法中引领蜂和观察蜂利用现有的食物源生成候选对象. 与侦察蜂相比，引领蜂和观察蜂的开发特征更占优势，为了将开发和侦察平衡地结合起来，本文引入特定控制参数LIMIT. 在ABC算法侦察蜂阶段，如果食物源的试用计数器由引领蜂和观察蜂更新后超过了极限值，则该食物源被丢弃，其引领蜂变成侦察蜂. 侦察蜂在没有使用引领蜂提供任何信息的情况下随机飞离蜂箱，并试图像式(7)中那样发现新的食物源. 通过考虑问题的属性来精确确定要分配给极限参数的值，也可以使用式(11)中给出的参数和解的数量来计算.

    其中SN为解的数量，N为矩阵S的时间序列，M为时间序列的大小.

3.   基于改进ABC算法的大数据优化

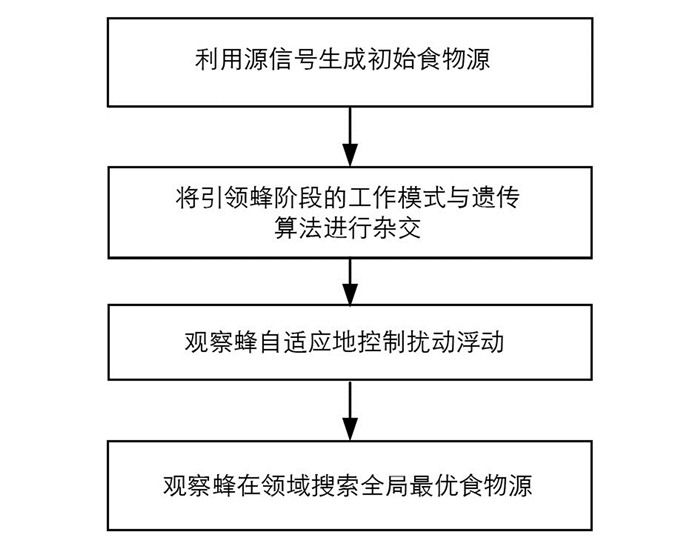
  • 标准ABC算法无法为基于EEG信号的大数据优化问题产生令人满意的结果，因此需要针对大数据优化问题的独特性质来对ABC算法进行改进. 改进ABC算法的具体流程如图 1所示.

    • 3.1.   使用源信号生成初始食物源

  • 标准ABC算法食物源的参数或维度初始值在给定的上下限内随机确定. 为了提高初始食物源或解的质量，分配给解决方案参数的值应该仔细选择，特别是对于大数据优化问题.

    在基于EEG信号的大数据优化问题中，用不同的元启发式算法找到合适的矩阵S1实际上是原始S矩阵的一部分，可以通过引导S矩阵产生初始解. 在所提出的生成模型中，将初始解所有参数直接设置为S矩阵的相应元素，然后通过在(-1e-05)和(+1e-05)之间均匀产生的随机数与S矩阵的适当元素相加进行修改.

    • 3.2.   基于遗传算子的引领蜂阶段

  • 标准ABC算法的引领蜂阶段仅通过扰动一个参数即可在储存的食物源附近生成候选解，但其有限的变异效应会降低收敛性能，特别是针对大数据优化的高维问题. 本文提出的算法在引领蜂阶段引入进化算法的全局最优解、特殊选择、交叉和变异算子信息. 用矩阵的形式来表示该技术对大数据优化问题产生的解，矩阵的每行对应一个独立的时间序列. 为了生成候选对象，应将每个时间序列及所有元素作为一个整体进行评估，即通过基于整个时间序列执行交叉算子和基于时间序列的元素执行变异算子来产生候选解.

    为了提高候选解的质量，采用轮盘赌选择机制来确定要交叉的食物来源，以提高合格候选解的选择概率. 在轮盘赌选择机制中，整个轮盘被分成切片或切槽，每个解用切片或切槽表示，轮盘的插槽尺寸根据个体的适应度值成比例地确定. 引领蜂与通过执行轮盘赌旋转而确定的食物来源相关联. 为了使用交叉遗传算法产生候选者，还需要第二参与者. 当考虑大数据优化问题的难度和决策参数的庞大数量时，可以确定全局最优解是交叉算子最合适的第二参与者.

    假设xi是完成轮盘赌反向选择之后分配给引领蜂的食物源，对应于包含大小为M的N个时间序列的解. xb是直到当前评估为止找到的全局最佳食物源，当尝试确定xi邻域内的候选食物源时，在用于确定交叉算子的可能分割点范围[0, N]处生成由d表示的随机整数. 分配d值后，分别从xi和xb食物源中取出索引为1~d的时间序列和索引为(d+1)~N的时间序列，并将其插入到候选解vi的适当位置. 如果d的值等于零，则将所有时间序列从xb复制到vi, 并且引领蜂有机会直接在全局最优解的附近进行搜索. 如果d的值等于N, 则所有的时间序列都从xi复制到vi, 并且引领蜂在离开之前有机会搜索记忆食物源的一个狭窄邻域.

    在本文所提算法的变异算子中，执行交叉操作后利用xi, xb或同时利用两者的信息生成vi个候选解，食物源vi变异后的候选解为

    式(12)中：Mr表示在[0, 1]区间取值的突变率，β为在(-1e-05)和(+1e-05)之间随机产生的常数. rnd为在[0, +1]范围内产生的随机数.

    计算食物源的适应度，如果vi食物源的适合度fit(vi)值高于食物源的适合度fit(xi)值，则引领蜂离开xi食物源. 此外，如果使用的蜜蜂阶段未完成，则轮盘赌的切片被重新计算. 否则，在将其试验计数器递增1之后，xi食物源在解决方案集中保持不变.

    • 3.3.   全局最优解引导观察蜂

  • 观察蜂选择引领蜂的食物源，并开始在它们周围寻找候选食物源. 为了提高观察蜂选择合格食物源的效率，将所有观察蜂送到全局最优食物源，并仅通过扰动一个参数即可产生敏感候选对象，从而提高改进ABC算法观察蜂阶段的开发能力.

    在算法的初始化阶段，通过在S矩阵的元素上添加(-1e-05)和(+1e-05)之间随机产生的数来生成解. 这种初始化机制导致两个不同解的相同参数之间的差异相对较小，当将该相对较小的差乘以[-1, +1]之间的随机数时，式(8)中的候选生成模型将完全失去其变化效果，并且会降低算法的收敛速度. 本文将xij和xkj参数之间的差乘以与默认配置相比在更宽范围内自适应地确定其幅度的系数(扰动幅度PM), 来提高扰动处理效率. 当为PM赋值时，φ系数在-PM~+PM间随机选择. 为了在给定PM参数的第一个值后对其进行自适应调整.

    Rechenberg 1/5突变规则，根据成功突变与所有突变的比率来确定新的参数，如果φ(m)显示的成功突变比率等于1/5, 则PM值保持不变. 否则，针对随后的围观蜜蜂阶段增加或减少PM值.

4.   实验结果与分析

  • 所有实验均在分布式大数据分析平台上进行，在具有Intel(R)Core(TM)i7-6500U处理器和8.00 GB内存的机器上进行，采用C语言对算法进行编程. 为了分析改进ABC算法的求解能力，对D4, D4N, D12, D12N, D19和D19N实例进行不同的控制参数赋值测试. 在PM为2~15时对本文算法进行测试后，发现PM合适的初始值为10, Mr值为0.75, 如果需要每个周期结束时应用Rechenberg 1/5变异规则来修改PM, 种群大小设置为100.

    表 1给出了在进行1 000个周期后，标准ABC算法、交叉ABC算法[15]与本文算法对D4, D4N, D12, D12N, D19和D19N实例的最佳目标函数值和平均最佳目标函数值.

    由表 1可以看出，与标准ABC算法和交叉ABC算法相比，本文提出的改进ABC算法获得了更稳健的最优和平均最优目标函数值. 这是因为对于所考虑的大数据优化问题，本文算法在引领蜂阶段使用专门的进化算子，并将所有的观察蜂发送到全局最优食物源，然后在其周围生成候选解，这比标准ABC算法的候选生成方法更方便，提高了该算法的求解能力

    表 2给出了本文算法与蜻蜓算法DA[14]、差分算法HDE[16]进行1 000个周期的最佳目标函数值和平均最佳目标函数值.

    由表 2可以看出，与其他元启发式算法相比，本文改进的ABC算法能够为所有6个问题实例产生更好的结果，本文算法的平均最佳目标函数值均优于其他算法. 这是因为本文算法在食物源初始化、引领蜂、观察蜂阶段所做的改进提高了该算法的求解能力.

5.   结语

  • 本文针对大数据优化问题的特点，提出了基于改进ABC算法的大数据优化信号重构算法. 该算法的食物源通过引导所考虑问题的现有信息来进行初始化，然后将引领蜂阶段与进化算法的特殊选择、交叉和变异算子进行杂交，最后对同一算法的观察蜂阶段采用Rechenberg 1/5变异规则自适应调整扰动幅度，在全局最优解的邻域内提供固定的搜索操作. 为了确定改进ABC算法的大数据优化技术得到解的适当性，将其用于解决CEC 2015大数据大赛上提出的大数据优化问题. 与其他算法相比，改进的ABC算法具有更稳健的最优和平均最优目标函数值，对大数据优化问题能够产生令人满意的结果. 未来的工作是采用不同的局部搜索和问题划分方法，进一步完善引领蜂、观察蜂和侦察蜂阶段的搜索机制.

参考文献 (16)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回