高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

基于PSO的航空遥感图像质量恢复算法

, 

上一篇

下一篇

谭晏松, 宋铁成. 基于PSO的航空遥感图像质量恢复算法[J]. 西南师范大学学报(自然科学版), 2021, 46(3): 13-19. doi: 10.13718/j.cnki.xsxb.2021.03.003
引用本文: 谭晏松, 宋铁成. 基于PSO的航空遥感图像质量恢复算法[J]. 西南师范大学学报(自然科学版), 2021, 46(3): 13-19. doi: 10.13718/j.cnki.xsxb.2021.03.003
shu
TAN Yan-song, SONG Tie-cheng. Restoration Algorithm of Aerial Remote Sensing Image Quality Based on PSO[J]. Journal of Southwest China Normal University(Natural Science Edition), 2021, 46(3): 13-19. doi: 10.13718/j.cnki.xsxb.2021.03.003
Citation: TAN Yan-song, SONG Tie-cheng. Restoration Algorithm of Aerial Remote Sensing Image Quality Based on PSO[J]. Journal of Southwest China Normal University(Natural Science Edition), 2021, 46(3): 13-19. doi: 10.13718/j.cnki.xsxb.2021.03.003
shu

基于PSO的航空遥感图像质量恢复算法

  • 1.

    重庆电子工程职业学院 人工智能与大数据学院，重庆 401331

  • 2.

    重庆邮电大学 通信与信息工程学院，重庆 400065

详细信息
    作者简介:

    谭晏松, 副教授, 主要从事软件工程研究 .

  • 中图分类号: TP391

Restoration Algorithm of Aerial Remote Sensing Image Quality Based on PSO

  • 1.

    School of Big Data and Artificial Intelligence, Chongqing College of Electronic Engineering, Chongqing 401331, China

  • 2.

    School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

  • 摘要: 针对现有航空遥感图像恢复算法中出现的冗余伪像和颜色失真现象, 提出一种基于PSO的航空遥感图像质量恢复算法.该算法通过有效的色彩平衡和饱和度调整、色彩还原以及基于粒子群优化(Particle Swarm Optimization, PSO)算法的对比度增强技术来恢复航空遥感图像的质量.实验结果表明: 与其他现有质量恢复方法相比, 通过定性和定量评估, 本文提出的方法可以产生更优的视觉图像, 表现出更好的性能.
    Abstract: Aiming at the phenomenon of redundant artifacts and color distortion in existing aerial remote sensing image restoration algorithms, a restoration algorithm of aerial remote sensing image quality based on PSO has beenproposed. Through effective color balance and saturation adjustment, color restoration and contrast enhancement technology based on particle swarm optimization(PSO) algorithm, the algorithm can restore the quality of aerial remote sensing image. The experimental results show that compared with other existing quality restoration methods by visual and quantitative assessments, the proposed method can produce better visual image and show better performance.
  • 加载中

  • 图 1  本文算法在3个步骤上的测试结果

    下载: 全尺寸图片 幻灯片

    图 2  USC-SIPI航空影像在不同质量恢复方法中的视觉效果

    下载: 全尺寸图片 幻灯片

    图 3  SZTAKI AirChange Benchmark航空影像在不同质量恢复方法中的视觉效果

    下载: 全尺寸图片 幻灯片

    表 1  不同算法在USC-SIPI数据集中的性能评价结果

    算法 DE BIQME NIQMC EME
    LSCN[7] 7.422 8 0.607 2 4.965 1 24.119 1
    MDE[8] 6.901 4 0.420 9 3.958 7 5.913 1
    JEI[14] 7.074 3 0.449 2 3.901 1 7.922 2
    OPHBE[15] 7.553 2 0.610 8 5.118 6 27.365 9
    本文算法 7.708 0 0.613 9 5.342 9 41.122 5
    下载: 导出CSV

    表 2  不同算法在SZTAKI数据集中的性能评价结果

    算法 DE BIQME NIQMC EME
    LSCN[7] 7.269 2 0.504 5 4.736 1 17.111 7
    MDE[8] 7.060 1 0.427 0 4.186 3 9.229 2
    JEI[14] 7.611 6 0.589 8 5.243 4 17.065 5
    OPHBE[15] 7.693 3 0.617 4 5.332 5 22.171 4
    本文算法 7.749 2 0.625 6 5.447 9 35.886 7
    下载: 导出CSV
  • [1] 赵伟, 曾亚. 重庆"一小时经济圈"城市扩展时空特征研究[J]. 西南师范大学学报(自然科学版), 2019, 44(5): 86-94. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xsxb.2019.05.015
    [2] AUDEBERT N, LE SAUX B, LEFÈVRE S. Segment-before-Detect: Vehicle Detection and Classification through Semantic Segmentation of Aerial Images[J]. Remote Sensing, 2017, 9(4): 368-385. doi: 10.3390/rs9040368
    [3] 张强, 李莲芳, 杨世琦, 等. GNSS-R陆面遥感为重要补充的土壤水分监测体系设计[J]. 西南大学学报(自然科学版), 2019, 41(3): 114-119. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-XNND201903017.htm
    [4] SINGH D, KUMAR V. Dehazing of Remote Sensing Images Using Improved Restoration Model Based Dark Channel Prior[J]. The Imaging Science Journal, 2017, 65(5): 282-292. doi: 10.1080/13682199.2017.1329792
    [5] 靳欢欢, 姚继锋, 钟裕标, 等. 一种适用于航空影像的无参考模糊探测方法[J]. 测绘科学, 2019, 44(6): 198-203. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201906029.htm
    [6] LUO S, SHEN H F, LI H F, et al. Shadow Removal Based on Separated Illumination Correction for Urban Aerial Remote Sensing Images[J]. Signal Processing, 2019, 165: 197-208. doi: 10.1016/j.sigpro.2019.06.039
    [7] ZHAN K, SHI J H, TENG J C, et al. Linking Synaptic Computation for Image Enhancement[J]. Neurocomputing, 2017, 238: 1-12. doi: 10.1016/j.neucom.2017.01.031
    [8] SURESH S, LAL S. Modified Differential Evolution Algorithm for Contrast and Brightness Enhancement of Satellite Images[J]. Applied Soft Computing, 2017, 61: 622-641. doi: 10.1016/j.asoc.2017.08.019
    [9] LIU C J, CHENG I, ZHANG Y, et al. Enhancement of Low Visibility Aerial Images Using Histogram Truncation and an Explicit Retinex Representation for Balancing Contrast and Color Consistency[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 128: 16-26. doi: 10.1016/j.isprsjprs.2017.02.016
    [10] KANG X D, HUANG Y F, LI S T, et al. Extended Random Walker for Shadow Detection in Very High Resolution Remote Sensing Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 56(2): 867-876.
    [11] MO N, ZHU R X, YAN L, et al. Deshadowing of Urban Airborne Imagery Based on Object-Oriented Automatic Shadow Detection and Regional Matching Compensation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(2): 585-605. doi: 10.1109/JSTARS.2017.2787116
    [12] 崔浩, 艾海滨, 张力, 等. 透射率全局估计航空影像去雾算法[J]. 遥感信息, 2019, 34(1): 102-110. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-YGXX201901014.htm
    [13] AGARWAL M, SRIVASTAVA G M S. Genetic Algorithm-Enabled Particle Swarm Optimization(PSOGA)-Based Task Scheduling in Cloud Computing Environment[J]. International Journal of Information Technology & Decision Making, 2018, 17(4): 1237-1267.
    [14] JMAL M, SOUIDENE W, ATTIA R. Efficient Cultural Heritage Image Restoration with Nonuniform Illumination Enhancement[J]. Journal of Electronic Imaging, 2017, 26(1): 1-15. doi: 10.1117/1.JEI.26.1.011029
    [15] WU H T, TANG S H, HUANG J W, et al. A Novel Reversible Data Hiding Method with Image Contrast Enhancement[J]. Signal Processing: Image Communication, 2018, 62: 64-73. doi: 10.1016/j.image.2017.12.006
    [16] ZHANG M Y, XU G L, CHEN K M, et al. Triplet-Based Semantic Relation Learning for Aerial Remote Sensing Image Change Detection[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(2): 266-270.
  • 加载中
图( 3) 表( 2)
计量
  • 文章访问数:  948
  • HTML全文浏览数:  948
  • PDF下载数:  79
  • 施引文献:  0
出版历程
  • 收稿日期:  2020-01-10
  • 刊出日期:  2021-03-20

基于PSO的航空遥感图像质量恢复算法

    作者简介: 谭晏松, 副教授, 主要从事软件工程研究
  • 1. 重庆电子工程职业学院 人工智能与大数据学院，重庆 401331
  • 2. 重庆邮电大学 通信与信息工程学院，重庆 400065
  • 收稿日期:  2020-01-10

摘要: 针对现有航空遥感图像恢复算法中出现的冗余伪像和颜色失真现象, 提出一种基于PSO的航空遥感图像质量恢复算法.该算法通过有效的色彩平衡和饱和度调整、色彩还原以及基于粒子群优化(Particle Swarm Optimization, PSO)算法的对比度增强技术来恢复航空遥感图像的质量.实验结果表明: 与其他现有质量恢复方法相比, 通过定性和定量评估, 本文提出的方法可以产生更优的视觉图像, 表现出更好的性能.

English Abstract

    全文HTML

  • 当前，遥感图像在空间、地球科学及军事侦察等领域中得到广泛的应用[1]. 遥感图像除了来自卫星拍摄之外，从飞机上捕获的空中遥感图像也是重要来源[2-3]. 航空影像具有高空间分辨率、高几何保真度及获取成本低的优点，在良好的天气条件下，大气对航空影像的影响甚至可以忽略不计. 但是，航空影像对天气的依赖性仍然很高，在雾霾天气时仍会遭受大气退化的困扰[4-5]. 因此，设计一种用于航空遥感图像质量增强的算法十分必要.

    尽管已经存在许多图像去雾和增强的方法，但是很多方法通常不适合航拍图像，如利用多张图像实现图像恢复的算法[6], 由于过度平滑导致图像信息丢失的链接模型算法[7]等. 为了解决这一问题，科研人员也提出了许多针对航空遥感图像去雾和图像增强的算法. Suresh等[8]提出了一种基于改进的差分演化(modified differentia evolution, MDE)算法来增强卫星图像的对比度，算法取得了很好的增强效果，但是该方法计算十分复杂. Liu等[9]提出了一种基于多尺度Retinex的低能见度航空图像增强方法，该方法通过平衡图像对比度和颜色一致性来对图像进行多尺度表示，并引入直方图截断技术作为后处理策略，有效提高了低能见度航空图像的质量. Kang等[10]提出了一种基于扩展随机游走器(Extended Random Walker, ERW)的阴影检测算法，该算法综合了阴影特性和相邻像素间的空间相关性，实现了去除航空图像阴影和增强对比度的效果. Mo等[11]提出了一种基于区域匹配的阴影补偿方法，该方法基于像素的软阴影检测，并用梯度滤波对软阴影图进行细化，然后利用区域匹配得到的最佳均匀非阴影区域对阴影区域进行补偿，使细节损失和亮度不平衡减少，从而获得极好的视觉效果. 崔浩等[12]针对雾霾天气会导致航空影像色彩失真和信息损失问题，提出了一种基于暗原色先验理论的航空影像去雾算法，该算法通过对透射率进行全局估计和局部优化，利用大气物理模型恢复图像，实现去雾效果.

    上述航空图像恢复方法在一定程度上取得了很好的增强效果，但是大多数方法会导致各种遥感图像上出现冗余伪像和颜色失真现象. 针对这一问题，本文提出了一种基于PSO的航空遥感图像质量增强算法，该算法通过有效的色彩平衡和饱和度调整、色彩还原及基于PSO算法的对比度增强技术，来实现遥感航空图像对比度增强和有效的色彩还原目的.

1.   粒子群优化算法

  • 粒子群优化(Particle Swarm Optimization, PSO)[13]算法属于元启发式算法，它是从自然界中各种生物的行为中获得灵感. 在PSO中，优化问题的潜在解可以表示为搜索空间中的粒子，所有粒子都存在相应的位置、速度和适应度值，粒子群优化就是在解空间中搜索最优粒子. 由于PSO算法中没有交叉阶段，意味着该方法在具有高探索度的粒子中提供高迁移率，能够找到兼具优化问题的最优解，属于全局随机搜索算法.

    PSO初始化为一群随机粒子，然后通过迭代找到最优解. 在每一次迭代中，粒子通过跟踪粒子本身所找到的最优解和整个种群目前找到的最优解两个极值来更新自己的位置和速度. 粒子群优化算法的大致运行步骤：①对粒子群中的每个粒子的位置和速度进行初始化；②计算每个粒子对应的适应度值并进行排序，从而找出当前全局最优的粒子；③从当前搜索到的全局最优粒子出发，更新每个粒子的位置和速度，重复多次迭代过程后，输出满足条件的最优解.

2.   基于PSO的图像质量恢复算法

  • 针对当前航空遥感图像对比度低和色彩失真的问题，本文提出一种图像质量恢复算法，用于提高图像对比度并进行有效的色彩还原. 该算法分3个步骤：①色彩平衡和饱和度调整；②有效的色彩还原；③基于PSO算法的对比度增强.

    • 2.1.   色彩平衡和饱和度调整

  • 给出一个RGB航空遥感图像I作为输入，以红色(R)、绿色(G)和蓝色(B)作为其通道，然后将其标准化为0和1, 如下所示：

    其中，(i, j)表示像素索引，[0, 1]是归一化幅度的范围，S表示遥感图像I标准化后的结果.

    根据灰色世界假设，平均图像颜色为灰色，从而消除了颜色投射. 为了保持这个假设，通道的平均颜色值应该是指数排列的. 此外，指数的使用确保所有像素值都在规定的范围内[0, 1]. 首先计算每个输入颜色通道平均亮度的最小值

    其中，SC表示C∈{R, G, B}的像素颜色幅度，N表示像素总数，它实际上是输入图像的宽度W与高度H的乘积，即N=W×H. 属于每个通道的平均值定义为

    然后，将每个颜色通道与平均图像亮度进一步对齐，并且采用每个像素的指数来完成.

    其中，κC表示每种颜色的指数.

    消除偏色后，再调整图像在色饱和强度(HSI)和色调饱和(HSV)颜色空间中的色彩饱和度(CS).

    从式(5)、式(6)可以看出，通过压缩或放大min{R, G, B}来增强饱和度. 因此，饱和度调整包括两个阶段.

    ① 要覆盖的所有像素量级都是全局对齐的[0, 1]

    其中，minC, WH{S}和maxC, WH{S}代表在所有颜色通道和像素上计算出的最小值和最大值. 在此过程后，至少一个具有最小颜色的像素将为零，并且至少一个具有最大颜色的像素将为1. 因此，像素将部分饱和. ②每个像素的颜色将分类为最小值β、中间值χ和最大值δ共3个部分，这3个值与颜色无关并满足条件β < χ < δ. 归一化后，定义一个变量μ

    通过调整中间元素与最小、最大范围比率来实现移位和缩放过程，即最小值和最大值的压缩和扩展可以通过调节参数λ(0 < λ < 1)来将所得元素保持在[0, 1]范围内.

    最小值和最大值的大小变化会导致颜色偏移，可以通过恢复最小值和最大值之间中间值的原始比率来降低.

    在这一步骤中，由于元素各自的排序索引，它们被重新映射到各自的颜色通道，并获得具有改进的饱和度的图像.

    • 2.2.   色彩还原

  • 步骤2采用一种颜色恢复技术处理步骤1中的RGB饱和图像，以消除任何类型的颜色冲突. 该技术为了使恢复图像满足人类的色彩视觉感知，将色彩保持在一个合理的色彩恒定度内[14]. 所采用的颜色恢复方法为

    其中，Ires和Is分别表示色彩还原图像与饱和度调整后的图像，C(i, j)表示色彩还原函数，可以定义为

    其中， $\hat{I}(i, j)$是基于色度学基础的颜色映射函数，Im(i, j)表示原始输入图像的第m个色带，n是图像通道的数量，η为控制非线性强度，λ为增益常数，本文中两个参数均取值0.2.

    • 2.3.   基于PSO算法的对比度增强

  • 在丰富了不均匀的照明区域后，需要在图像亮度上进行对比度增强处理. 此过程需要非锐化掩模滤波器(Unsharp Masking Filter, UMF). 首先将处理后的RGB图像转换为HSV空间，其中颜色由色彩H表示，颜色的丰富度由饱和度S表示，亮度值由V表示. 在V-通道上执行非锐化掩模增强，UMF的操作可以定义为

    其中，Z是滤波后的V-通道像素，s表示控制因子，决定增强的强度，X表示来自内核的边缘信号.

    UMF的性能在很大程度上取决于所使用的滤波器内核和增益因子的正确设置. 增益因子设置不当会使输出产生增强不足或过增强现象. 内核用于提取局部边缘，当选取过小时会强化噪声，导致对比度增强效果不明显，而选择过大时容易出现伪影. 通过综合考虑，本文取一个3×3大小的内核ζ, 从而在增强图像中提取更薄的边缘和更高的清晰度.

    内核元素的约束由参数a > 0给出. 从内核输出的边缘信号可以表示为

    其中，Δ是分布在像素V周围的3×3邻域像素.

    式(17)输出结果的缩放由控制参数s决定，并且会将其添加到原始图像中，以获得增强的清晰度. 为了获得期望的增强结果，需要PSO算法优化内核参数a和s. 为此，使用这些参数对PSO算法中的粒子进行编码.

    PSO算法中的群由q个粒子组成，即Tj, j=1, …, q. 在潜在解空间中，以随机方式为粒子分配其初始位置. 首先对解空间的总体大小P和最大代数G进行初始化，然后根据粒子的目标函数对其进行更新，并在多个时间步长i=1, …, G中，将其引导至最佳解决方案. 粒子在解空间中徘徊，并被当前的全局最优解Tg吸引. 粒子的运动由其当前最优解 $T_{i}^{q}$控制. 粒子的新位置取决于其原始位置和运动速度. 新的速度矢量由式(19)给出

    其中，v表示速度矢量，n表示惯性常数. 加速度常数表示为cg和cq, 它们是[0, cmax]中的随机数，cmax是介于1.7~2.0之间的最大值.

    根据新的速度，可以更新粒子的新位置

    为了满足a > 0和s > 0两个约束，可以定义为

    通过最大化目标函数来确定信息内容

    其中，ε表示熵，σ表示超范围像素的数量. 经过式(22)后，更新输出边缘信号X并按参数s缩放后，将其叠加到给定的V-通道图像V上，获得具有更高对比度的增强输出V-通道图像Z, 然后将其转换回RGB空间，输出最终的增强图像.

    本文算法分为3个主要阶段，为了更形象地表示，图 1给出了本文算法在3个步骤上的具体中间结果. 从图 1可以看出，低分辨率和颜色失真的图像经过饱和度调整、色彩还原和对比度增强后，可以获得高质量的航空遥感图像.

3.   实验结果与分析

  • 本文所有实验在一台配置为Intel(R) Core(TM)i7-7820X CPU @3.60 GHz和8 GB RAM的机器上进行，所有测试均在Matlab 2017a环境下实现. 采用USC-SIPI图像数据集[15]和SZTAKI AirChange Benchmark数据集[16]两组数据集中的数据用以评价本文方法的性能，并将实验结果与其他图像质量恢复算法，如链接模型算法LSCN [7]、改进的差分演化算法MDE[8]、基于色调映射和同态滤波的JEI算法[14]和序列直方图二进制扩展算法OPHBE[15]等进行比较.

    • 3.1.   数据集和参数设置

  • 在实验测试中，使用了来自USC-SIPI图像数据集和SZTAKI AirChange Benchmark数据集中不同的测试航空遥感图像. USC-SIPI图像数据集包含总共37幅航空遥感图像，这些图像最初以标签图像文件格式(Tag Image File Format，TIFF)存储，其中12幅航空图像的分辨率为512×512，25幅航空图像的分辨率为1 024×1 024. SZTAKI AirChange Benchmark数据集总共包含12幅航空变化检测遥感图像，这些图像最初以位图(Bitmap，BMP)颜色格式存储，每个航空图像的尺寸为952×640.

    本文中使用的实验参数大致设置为解空间的总体大小P=30, 最大代数G=30, PSO算法中的粒子数目q=2, 初始速度值v=0, 惯性常数n=0.8, 加速度常数cg=cq=1.7.

    • 3.2.   定性结果分析

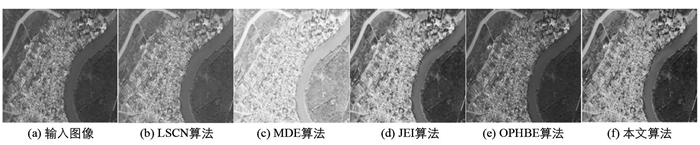
  • 图 2、图 3给出了不同算法利用USC-SIPI和SZTAKI AirChange Benchmark数据集中图像进行的定性增强结果. 从图 2、图 3可以看出，LSCN方法在视觉质量恢复过程中存在边缘信息丢失和振铃效应的现象. JEI方法的视觉质量恢复具有较好的输出效果，但在输出图像中缺少自然性. 利用MDE方法恢复的图像可以得到一个较好的增强结果，但是输出的图像中存在细微边缘和特征过于平滑的现象. OPHBE方法可以提供较好的细节显示和颜色自然度，只是在低亮度区域表现不佳. 与其他几种方法相比，本文方法关注局部细节和色彩平衡，相应的梯度和纹理也相对比较清晰. 因此，本文方法在对比度增强、亮度适应、细节保存和自然色彩之间取得了良好的平衡.

    • 3.3.   定量结果分析

  • 客观评价是通过对各算法结果的指标进行计算，利用图像的离散信息熵(Discrete Entropy，DE)、增强图像的盲图像质量测量(Blind Image Quality Measure of Enhanced images，BIQME)、无参考图像质量度量对比度失真(No Reference Image Quality Metric for Contrast distortion，NIQMC)和增强测度(EME)4个无参考量为评价指标来验证算法的有效性.

    离散信息熵DE代表图像的信息含量，其值越高，说明图像质量越好.

    其中，P(Xi)表示事件Xi发生的概率.

    NIQMC代表图像对比度扭曲的程度，指标的高值表示更丰富的图像色彩.

    其中，γ是权重系数，表示局部和全局之间的相对比例，QL=max{El1, El2, …, El5}和QG=DJS(h, u)分别表示局部变量和全局变量，Eli表示像素li的熵值，DJS(h, u)表示直方图h和像素u的JS散度.

    增强测度EME可由下式给出，其值越大，对比度越高.

    其中，I(i, j)表示原图中互不重叠的某一子块，k1k2表示子块个数.

    BIQME方法从对比度、清晰度、亮度、色彩艳丽度和自然度等方面反映图像的质量，是一种全局的无参考评价方法，其值越大表示图像整体质量越好.

    其中，M表示像素个数，Qmi, Qcc, Qsd, Qcs分别表示原始图像和还原图像在平均强度、对比度变化、结构畸变和色彩饱和度方面的相似性.

    表 1、表 2给出了不同方法利用USC-SIPI和SZTAKI AirChange Benchmark数据集中图像进行定量测试的结果，每个评价指标都是数据集所有图像实验结果的平均值. 对比表 1、表 2中性能指标可以发现，与现有的其他遥感增强方法相比，本文算法的质量参数具有明显的优势.

4.   结语

  • 本文提出一种基于粒子群优化的航空遥感图像质量恢复算法，解决了当前航空遥感图像恢复算法中出现的颜色失真、冗余伪像及信息损失等问题. 该算法可以分为色彩平衡和饱和度调整、有效的色彩还原和基于PSO算法的对比度增强技术3个步骤，从而达到恢复图像质量的目的. 实验结果表明：与其他算法相比，本文算法具有明显优势，可以产生纹理细节清晰度高和色彩自然的视觉图像，表现出更强的图像恢复性能.

参考文献 (16)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回