-
无线传感器网络[1]是指某一区域内的若干个组织良好的分散传感器所形成的无线多跳网络,用于监视和收集来自其周围环境的实时数据,并将这些数据汇总至预定的基站节点. 由于传统WSN存在部署节点策略和网络功能不够灵活、网络资源利用率低以及管理困难等问题,研究人员开发了基于软件定义网络的无线传感器网络[2]. 软件定义无线传感器网络是将网络中的传感器节点进行软件定义,让网络节点得到统一管理,降低节点能耗与部署成本,优化了路由性能,提高WSN的资源利用率[3].
在无线传感器网络使用过程中,传感器节点采集的大量数据需要由无线网络上传至预定基站或者控制器,数据上传路径的选择会直接影响数据的传输速率和传感器的寿命,因此WSN路径优化的目标是在保证数据正常传输的条件下,尽量降低节点能耗,延长整个网络的生命周期[4]. 由于路由问题在WSN中的重要性,引起了众多研究人员的关注. Kaur等[5]为了提高传感器寿命,提出了一种基于蚁群算法和粒子群算法的能量有效聚类和基于树的路由协议,通过基于蚁群和粒子群算法的混合数据聚合来改进簇间数据聚合,提高了网络的生存期. 冉涌[6]提出了一种多事件节能的无线网络传感器协议,该协议采用蚁群优化算法对节点活动和簇间通信进行优化,实现高效节能的目的. 但是,现有的WSN路由协议大多采用分布式算法,在分簇与路由选择间进行大量的信息交换,不适用于软件定义无线传感器网络范例. SDWSN的路由功能主要在集中的控制器中体现,在控制消息中收集链路、节点的状态信息,考虑网络节点的负载问题. Younus等[7]提出了一种用于软件定义无线传感器网络的能量感知多跳路由协议,该算法在网络生存期、平均能耗、分组传递率和时延方面均表现出良好的效果. 近年来,由于群体智能算法具有高效的搜索能力,许多学者将这类算法应用到SDWSN路径优化问题当中. Kumar等[8]提出了一种基于多核并行自适应粒子群优化的无线传感器网络绿色路由算法,该算法在SDWSN的框架下,采用Fork-Join模式的自适应粒子群优化对控制节点的数量和位置进行优化,达到绿色路由和延迟网络寿命的目的. 胡敏等[9]针对现有SDWSN路由协议中存在簇头能量消耗不均衡导致网络生存周期短和能量利用率低的问题,提出了一种基于扰动粒子群优化的能耗均衡路由算法,通过考虑节点的剩余能量、位置和能量来选择簇头,并利用改进粒子群算法来搜索更新最优簇头,在节点能耗均衡方面取得很好的效果,但是该算法仅适用于小型SDWSN网络.
虽然群智能优化方法对SDWSN网络中的路由起到优化作用,但这些算法也存在自身的不足,容易出现局部最优、收敛速度慢和精度不够等问题. 因此,针对SDWSN网络中的路径优化问题,本文提出了一种基于海豚回声定位算法的SDWSN路由算法,该算法通过考虑节点的剩余能量,采用海豚回声定位算法优化WSN中的局部和全局路径,从而实现节约能量,提高传感器网络寿命的目标.
全文HTML
-
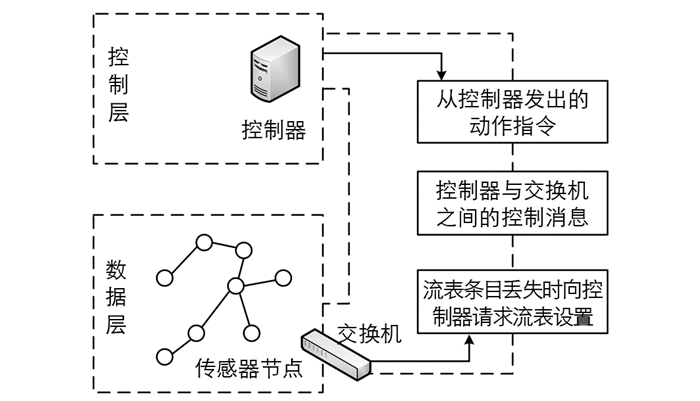
软件定义无线传感器网络是Luo等[10]在2012年首次将SDN引入WSN中,利用软件定义网络的优势解决无线传感器网络中的一些固有问题,与传统的WSN相比,SDWSN范例可以对无线传感器节点进行随机或统一的部署. 图 1给出了一个简单的SDWSN模型,从图中可以看到,SDWSN模型可以分为控制平面和数据平面两个部分,控制平面由控制器组成,用于执行控制器的数据指令或通过路由决策,数据平面由传感器节点和交换机组成,负责数据采集和转发.
-
当网络节点发送kbit数据到距离为d m处的相邻节点时,需要消耗的能量为
式中:Eelec表示接受和发送1bit数据时电路的功耗系数,εfs和εmp分别表示自由空间和多径衰落模型下的功耗常数.
同理,节点接收和处理kbit数据的能量消耗为
式中:Eda表示处理1bit数据时的能耗.
-
假设节点0和节点Y之间的传输距离为d,速率为rc,则成功传输的概率可以表示为
式中:γ表示速率rc对应的信干噪比(Signal to Interference plus Noise Ratio,SINR),Pidle(Y)表示节点Y的空闲概率.
根据幂律路径的损耗模型,上式可以修改为
式中:v表示节点遵循Poisson分布时的空间强度,α表示衰减因子,P和N分别表示节点的传输功率和噪声功率.
经过公式推导,最佳传输距离d′和最大吞吐量S′为
1.1. 网络模型
1.2. 能耗模型
1.3. 数据传输模型
-
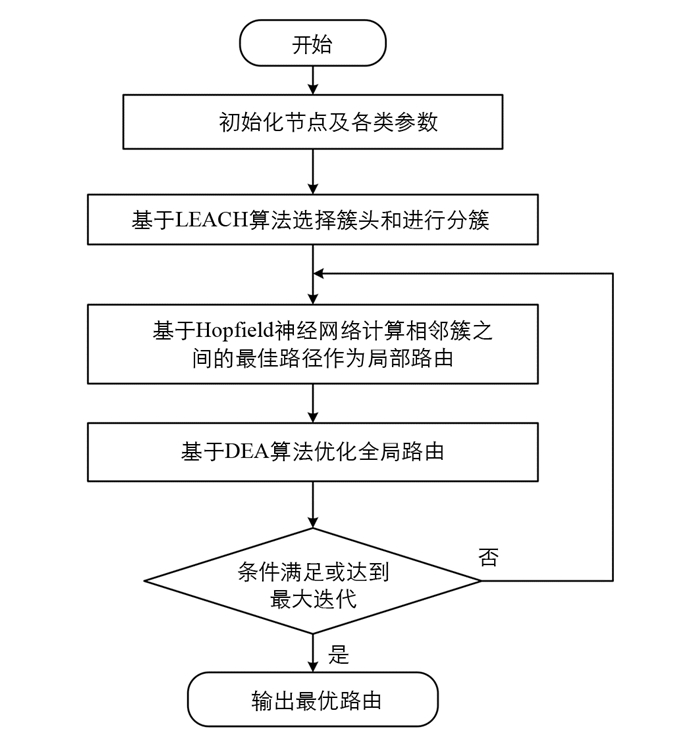
目标跟踪一直是无线传感器网络的热点,随着多媒体和实时传输新技术的出现,对目标跟踪路由的传输性能提出了新的要求. 因此,本文以无线传感器网络的吞吐量和能耗为指标,提出了一种基于海豚回声定位算法((Dolphin Echolocation Algorithm,DEA))的SDWSN路由算法,该算法包括簇头选择、局部路径规划和全局路径优化3个部分,算法流程如图 2所示.
-
簇头选择是将无线传感器网络中的所有传感器划分为多个簇,本文使用低功耗自适应集簇分层型协议(Low Energy Adaptive Clustering Hierarchy,LEACH) [11]对所有节点进行簇头选举. 簇头选出之后,将向周围节点广播自己成为簇头的消息,簇成员根据收到的广播消息选择距离自己最近的簇头加入该簇,并发送包含自己位置和剩余能量的信息.
-
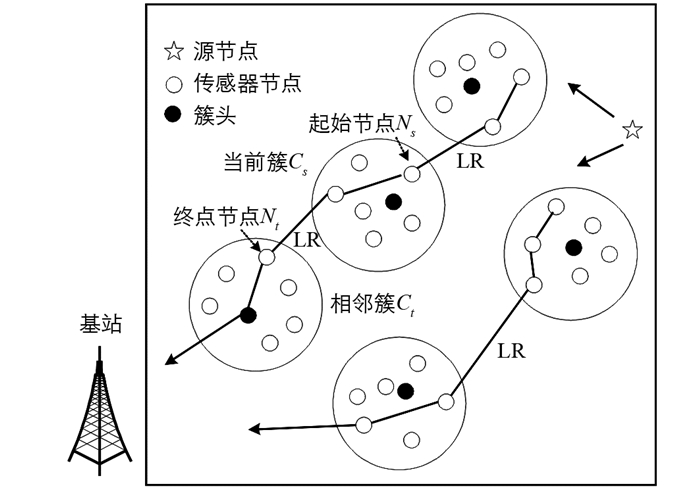
成簇结束后,WSN采用多跳路由技术,在相邻簇之间构造局部路由(Local Routing,LR),如图 3所示. 局部路径的起始点是当前簇Cs中的节点Ns,终点为簇Ct中靠近Cs的节点Nt. 从簇Cs到相邻簇Ct的局部路由集LR(Cs,Ct)被定义为从Cs中的任意节点到Ct中与Cs相邻的所有节点的最优路径. 对于局部路由LR,以吞吐量和能耗为优化目标,适应函数表示为
式中:T表示吞吐量,E表示能量,α表示常数,Ns表示当前簇Cs中的起始节点,Nt表示相邻簇的终点节点.
局部路径的优化借鉴Zhao等[12]计算的最优路径,使用Hopfield神经网络算法计算相邻簇之间的最佳路径作为局部路由,该步骤中的复杂度为O(N),因为假定神经元个数为N,行和列的约束可以看作是约束广度优先搜索,因此,每个路径规划周期的时间复杂度为O(N).
-
全局路径优化的目的是通过选择相邻簇之间的最优路由来构建从目标到宿节点的信息传输完整路径. 对于全局路径,同样以最大化吞吐量和能量消耗效率为目标,在优化过程中涉及多个簇群. 基于LR,全局路径(Global Routing,GR)根据服务需求实现端到端路由优化,所有计算出的局部路径都被分割成P1,…,Pk的集合. 当满足约束条件时,从每个集合中选择一条路径,以形成使目标函数最大化的路径,即为全局路由GR选择最佳路径. 全局路由选择问题可以转换为多选背包问题,目标函数可以表示为
式中:k是路径集合的数量,qp表示第P个集合中路径数,Vpq是p集合中q路径的函数值,此处需要考虑两个约束条件:一个约束条件是需要从每个路径集中选择局部路径,另一个是必须从直接或间接互连的簇中选择局部路径,本文采用DEA算法对全局路径进行优化.
海豚回声定位算法是由Mahesh等[13]开发的一种离散元启发式优化算法. 该算法从海豚利用回声定位的优势发现自然环境并捕食猎物中得到启发,海豚最初在搜索空间周围进行搜索猎物,一旦海豚接近目标,则限制搜索空间,集中精力搜索目标位置,并逐渐增加点击次数. DEA方法可以分为两个阶段:第一阶段,算法执行全局搜索,通过探索一些随机位置来探索整个搜索空间;第二阶段,围绕全局搜索结果进行精确的局部位置搜索,即算法逐渐按照用户定义的曲线进行局部搜索,在DEA算法搜索到目标之前的每一步中,获得接近最优解的概率都会增加.
基于DEA算法的全局路径步骤如下:
步骤1:参数初始化,设定最大循环数N,随机生成NL个可行解,初始化维度为NL×NV的位置矩阵L =[L1,L2,…,LNL],其中NL为海豚需要搜寻位置的数量,NV表示变量数量.
步骤2:将所有计算出的局部路由分割成P1,…,Pk的集,然后根据公式(11)计算每一个变量的目标函数值GR(Li).
步骤3:计算当前循环的收敛因子CF:
式中:CF(pi)用来表示每一次迭代的最优解为全局最优解的概率,CF1表示第一个循环最优解为全局最优解的概率,pi表示第i个循环,N表示循环总次数,p表示收敛曲线次数,通过调整p来修改收敛曲线的形状.
步骤4:计算每个变量的累计适应度,在该步骤中,搜索空间划分为两个区域,即半径为Re的受影响区域和不受影响的其他区域:
式中:k∈[-Re,Re],Aij为Li(j)在Aj中的位置,AF(Aij+k,j)是第j个变量的第(Aij+k)个可取值的累积适应度.
步骤5:查找最佳位置,最优AF对应最佳位置. 因此,如果满足终止条件时,算法终止;否则,查找分配给最佳位置变量的替代方案,令最佳位置处的AF=0.
步骤6:概率确定与分配,对于每个变量lj,计算每一个可取值Aj(i)的概率值:
式中:LAj表示Aj向量的长度. 将当前循环中预定义概率CF(pi)分配给最佳位置所对应各个变量,(1-CF(pi))分配给其他可行值.
步骤7:下次迭代的位置选择,根据计算出的概率值生成下次迭代的NL个可行解.
步骤8:回到步骤2,直到满足条件为止.
基于DEA的全局路径优化的复杂性的大小取决于最大迭代数N和变量数量NV及位置数量NL,以及计算步骤中对累计适应度和概率值等参数的计算. 因此复杂度为O(N×NL×NV+N+ N×NL),时间复杂度是解决问题大小的函数,故时间复杂度为O(N×NL×NV).
2.1. 簇头选择
2.2. 局部路径规划
2.3. 基于DEA的全局路径优化
-
为了评价所提算法的性能,使用MATLAB R2018a软件进行SDWSN优化算法的测试实验,并在相同条件下与蚁群优化算法(Ant Colony Optimization,ACO)[14]、粒子群多优化(Partical Swarm Optimization,PSO)[15]以及灰狼优化算法(Grey Wolf Optimizer,GWO)[16]的任务调度方法相比. 表 1给出了仿真实验环境的详细信息.
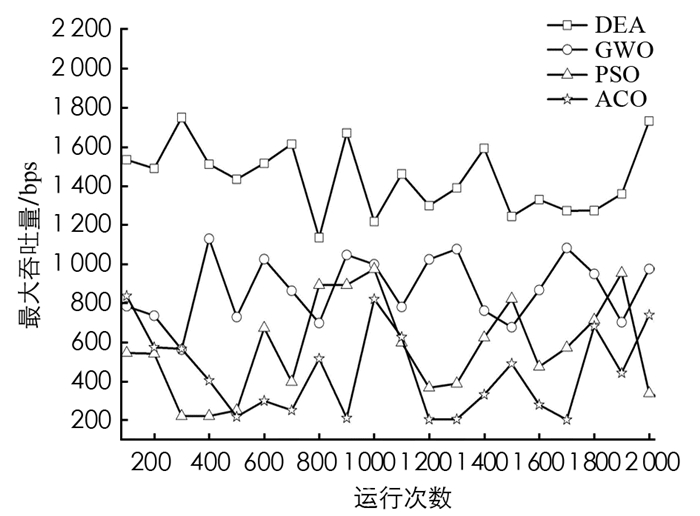
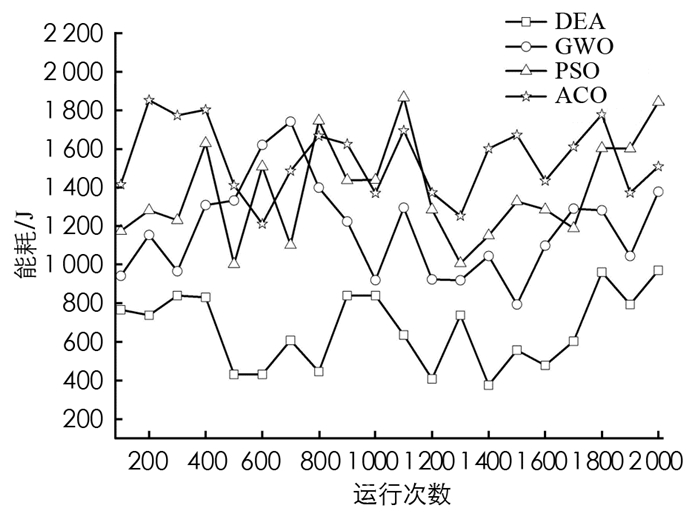
在第一个实验中考虑了45个传感器和9个簇,每个簇具有5个传感器. 对于给定的优化问题,提出的算法与其他对比算法的测试结果进行了比较. 图 4和图 5分别给出了不同优化算法在吞吐量和能量方面获得的结果. 由于DEA、ACO、PSO以及WGO优化算法都是随机性质的算法,因此,测试过程中,在MATLAB工具上对各个算法进行了多次运行仿真,每次运行执行100次迭代,产生一个最优解,多次运行的结果是基于均值公式计算出所有最佳值的平均值.
从图中可以看出,相较于其他算法,所提出的算法在实现最大吞吐量和最小能量消耗方面具有更好的效果. 在图中,DEA在每个区间(从100到2000)产生平均最优解. 因此,DEA算法在给定的实验场景下,在有效地求解出两个目标函数的最优解的同时,也表现出了较好的收敛性.
为了评估所提出的算法在不同规模的SDWSN网络中的性能,在第二个实验中,将不同的算法应用于不同规模的网络模型,如具有20,50,80个传感器以及对应4,10,16个簇的网络模型,用于探索吞吐量和能耗目标函数的最优和最差解,对于吞吐量,最优解是最大吞吐量值,最差解是最小吞吐量值. 然而,在能耗目标函数的情况下,最小值是最优的,最大值是最差解. 表 2-表 3给出了不同规模的网络模型在吞吐量和能耗方面的测试结果. 从表 2和表 3可以看出,与其他算法相比,DEA算法在吞吐量和能耗目标函数方面都能产生最佳解. 在表 2中,对于50个传感器网络,DEA具有901.2 bps作为最大吞吐量的最优解,而其他算法产生次最优解. 在表 3中,DEA算法的能量消耗是给定网络规模中的最小值. 实验表明,DEA算法在SDWSN网络吞吐量和能耗准则上具有最小的损伤.
-
本文以传感器的吞吐量和能量利用率为参数,提出了一种基于海豚回声定位优化算法,用于解决SDWSN网络模型中分布式传感器存在能量消耗大以及网络寿命低等问题. 该算法将SDWSN分为多个域,通过考虑每个域中驻留的传感器数以及节点的剩余能量,利用海豚回声定位算法优化SDWSN中的路由选择来实现节约能量,提高传感器网络寿命的目标. 实验表明,对于给定的优化问题,DEA算法相比于其他算法具有更好的性能,在两个目标函数上都获得了SDWSN中的最优解.



 下载:
下载: