在本文中，$\mathbb{Z}$⁺，$\mathbb{R}$，$\mathbb{R}$ⁿ，$\mathbb{C}$ⁿ和$\mathbb{C}$^n×n分别表示正整数集，实数集，n维实向量空间，n维复向量空间及n×n复矩阵空间. E_n表示n×n维单位矩阵，对一个正整数N，记集合$\vec N$ ={1，2，…，N}. 对任意的x∈$\mathbb{C}$ⁿ，x^H表示x的共轭转置，$\left\| \mathit{\boldsymbol{x}} \right\| = \sqrt {{\mathit{\boldsymbol{x}}^{\rm{H}}}\mathit{\boldsymbol{x}}} $. $\mathbb{G}$=(V，ε)表示由点集V={1，2，…，N}和边集ε∈V×V构成的图. 对任意两个节点l，k∈V，(l，k)∈ε表示节点l与k之间的无向连边. {G_k}_k=1^T是T个$\mathbb{G}$均含有N个节点的子图构成的图序列.

考虑由N个复值神经网络构成的复杂网络系统，其模型描述为：

式(1)中x_i(t)=(x_i1(t)，x_i2(t)，…，x_in(t))^T∈$\mathbb{C}$ⁿ表示第i个神经网络的状态向量，对角矩阵A∈$\mathbb{C}$^n×n表示神经网络的自抑制矩阵，f(x_i(t))=(f₁(x_i1(t))，f₂(x_i2(t))，…，f_n(x_in(t)))^T∈$\mathbb{C}$ⁿ表示神经网络的激活函数，D∈$\mathbb{C}$^n×n表示神经网络内部连接权重矩阵，I(t)是n维的外部输入向量值函数，U_i(t)刻画了网络节点之间的脉冲耦合机制，其具体形式为：

式(2)中t_k表示脉冲时刻满足0 < γ₁ < t_k+1－t_k < γ₂，δ(·)是Dirac脉冲函数，实矩阵Ω_k=(ω_ij(t_k))_N×N∈$\mathbb{R}$^N×N表示t_k时刻切换拓扑对应的邻接矩阵，对任意i，j∈V，若存在(i，j)∈ε，那么ω_ij(t_k)>0，否则ω_ij(t_k)=0. 另外，记G_k为t_k时刻的网络拓扑，$\mathop {\lim }\limits_{t \to t\bar k} {\mathit{\boldsymbol{x}}_i}(t) = {\mathit{\boldsymbol{x}}_i}\left({{t_k}} \right)$.

利用Dirac函数性质，式(1)转化为如下脉冲微分系统

令

则式(3)转化为：

下面给出一些相关的定义、假设和引理.

定义1   对图$\mathbb{G}$=(V，ε)及非空点集L⊆V，称集合$\mathbb{N}$($\mathbb{G}$，L)={k∈V\L|∃l∈L，(l，k)∈ε}为点集L在图$\mathbb{G}$中的邻居节点集.

定义2   对图序列{G_k}_k=1^T，若∪_k=1^TG_k中包含图$\mathbb{G}$的一个生成树，则称图序列{G_k}_k=1^T是节点连通的.

定义3^[17]   对给定图序列{G_k}_k=1^T，若存在一个节点l∈V使得V_k≤V_k－1∪$\mathbb{N}$(G_k，V_k－1)，其中V₀={l}，V_T=V，则称图序列{G_k}_k=1^T是序列连通的.

定义4   对任意i，p∈V，若$\mathop {\lim }\limits_{t \to + \infty } \left\| {{\mathit{\boldsymbol{x}}_i}(t) - {\mathit{\boldsymbol{x}}_p}(t)} \right\| = 0$，则称耦合神经网络式(1)是全局渐近同步的.

定义5^[18]    对给定向量Q=(x₁x₂，…，x_n)∈$\mathbb{R}$ⁿ，称conv(Q)={∑_i=1^mα_ix_i：∑_i=1^mα_i=1，α_i≥0，m≥1}为向量Q的凸包.

假设1   对任意k∈$\mathbb{Z}$⁺，当i≠j时，0≤ω_ij(t_k) < 1，并且0≤∑_j=1，j≠i^Nω_ij(t_k) < 1.

假设2   对任意x，y∈$\mathbb{C}$ⁿ，存在正常数$\mathscr{L}$使得‖f(x)－f(y)‖≤ L ‖x－y‖.

引理1^[17]   若对任意l∈$\mathbb{Z}$⁺，图序列{G_k}_k=(l－1)T+1^lT是节点连通的，那么图序列{G_k}_k=1^(N－1)2T是序列连通的.

引理2^[17]   设x∈I⊆$\mathbb{R}$，常数a≤b，则函数f(x)=ax+(1－x)b在${x^*} = \mathop {\min }\limits_{x \in I} \{ x\} $处取得最大值.

为方便证明，首先引入如下记号.

定理1   基于假设1、假设2，如果存在正整数T使得对任意l≥0，图序列{G_k}_lT+1^(l+1)T是序列连通的，并且

那么，脉冲耦合复值神经网络式(1)是全局渐近同步的.

证  第一步：证明φ(t_k⁺)≤φ(t_k).

对任意i∈V，由假设1可知

因此，由i的任意性可知Φ(t_k⁺)⊆Φ(t_k)，从而可得φ(t_k⁺)≤φ(t_k).

第二步：证明对任意的k∈$ \mathbb{Z} $⁺， $\varphi \left({{t_k}} \right) \le {{\rm{e}}^{\frac{{\tilde \delta }}{2}\gamma }}\varphi \left({t_{k - 1}^ + } \right), {\varphi _k} \le {{\rm{e}}^{\frac{{\tilde \delta }}{2}\gamma }}{\hat \varphi _{k - 1}}$.

当t∈(t_k－1，t_k]时，对任意i，p∈V，定义e_ip(t)=x_i(t)－x_p(t)，由式(4)可知

其中$\mathit{\boldsymbol{\tilde f}}\left({{\mathit{\boldsymbol{e}}_{ip}}(t)} \right) = \mathit{\boldsymbol{f}}\left({{\mathit{\boldsymbol{x}}_i}(t)} \right) - \mathit{\boldsymbol{f}}\left({{\mathit{\boldsymbol{x}}_p}(t)} \right)$.由假设2可得

从而有

由节点i，p的任意性可得

第三步：证明若图序列{G_k}_k=1^T是序列连通的，则$\varphi \left({{t_{T + 1}}} \right) \le {{\rm{e}}^{\frac{{\bar \delta }}{2}\gamma T}}\left({1 - \prod_{s = 1}^T \alpha \left({{t_s}} \right)} \right)\varphi \left({{t_1}} \right)$.

结合式(4)和定义3可知，对任意i∈V_k，

由于$\mathop {\max }\limits_{j \in {V_{k - 1}}} \left\{ {\left\| {{\mathit{\boldsymbol{x}}_j}\left({{t_k}} \right)} \right\|} \right\} \le \mathop {\max }\limits_{j \in V} \left\{ {\left\| {{\mathit{\boldsymbol{x}}_j}\left({{t_k}} \right)} \right\|} \right\}$，根据引理2可知

因此，${\mathit{\hat \Phi }_k} \subseteq \alpha \left({{t_k}} \right){\mathit{\Phi }_k} + \left({1 - \alpha \left({{t_k}} \right)} \right)\mathit{\Phi }\left({{t_k}} \right), {\hat \varphi _k} \le \alpha \left({{t_k}} \right){\varphi _k} + \left({1 - \alpha \left({{t_k}} \right)} \right)\varphi \left({{t_k}} \right)$. 另外，结合第一步和第二步不难得到：${\varphi _k} \le {{\rm{e}}^{\frac{{\tilde \delta }}{2}\gamma }}{\hat \varphi _{k - 1}}, \varphi \left({{t_k}} \right) \le {{\rm{e}}^{\frac{{\tilde \delta }}{2}\gamma }}\varphi \left({t_{k - 1}^ + } \right) \le {{\rm{e}}^{\frac{{\tilde \delta }}{2}\gamma }}\varphi \left({{t_{k - 1}}} \right)$.因此，逐次迭代可得

由V₀是孤立节点集和V_T=V可知

结合第二步可得

所以

由定理条件和式(7)可知，$\mathop {\lim }\limits_{l \to \infty } \varphi \left({{t_{lT + 1}}} \right) = 0$，从而耦合神经网络式(1)是全局渐近同步的.

注1   当∏_s=1^Tα(t_s)=1时，虽然式(5)仍然成立，但在该条件下∑_j=1，j≠i^Nω_ij(t_k)≥1，这与假设1矛盾，并且由式(7)可知，此时无法得到网络的渐近同步性.因此0 < 1－∏_s=1^Tα(t_s) < 1.

推论1   基于假设1、假设2，如果存在正整数T使得对任意l≥0，图序列{G_k}_k=lT+1^(l+1)T是节点连通的，并且

那么耦合复值神经网络式(1)是全局渐近同步的.

注2  在定理1中，不连续脉冲切换拓扑下的序列连通性可解释为：t₀时刻某一复值神经网络节点V₀接收到外来信息，在t₁时刻拓扑结构切换为G₁，V₀在G₁中将信息传递给邻居节点$\mathbb{N}$(G₁，V₀)，此时信息遍历的节点集为V₁=V₀∪$\mathbb{N}$(G₁，V₀).随后，在t₂时刻拓扑结构切换为G₂，V₁中的节点在G₂中将信息传递给邻居$\mathbb{N}$(G₂，V₁)，此时V₂=V₁∪$\mathbb{N}$(G₂，V₁). 以此类推，在t_T时刻拓扑结构切换第T次时，V_T－1在G_T中与其邻居$\mathbb{N}$(G_T，V_T－1) 交换信息，此时V_T=V_T－1∪$\mathbb{N}$(G_T，V_T－1)=V，通过T次切换实现了整个网络的信息遍历，但每次切换的网络拓扑并不总是连通的.

注3   与文献[14-18]讨论的实值耦合神经网络相比，本文研究的脉冲耦合复值神经网络具有更强的信息存储能力和更高效的信息处理能力.在研究方法上，与传统的Lyapunov方法不同，本文主要运用直接误差方法和凸组合技巧来分析耦合网络的同步，理论分析和判定条件更简洁直观.

考虑6个具有双复值神经元的神经网络耦合而成的复杂网络，其模型为：

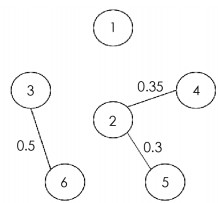
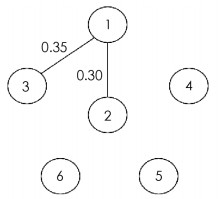
式(8)中x_i(t)∈$\mathbb{C}$²，U_i(t)为脉冲耦合策略式(2)，f(x_i)=(0.7tanh(x_i1(t))，0.7tanh(x_i2(t)))^T

耦合网络式(8)的脉冲拓扑切换图序列如图 1和图 2所示，这里V₀={1}，V₁={1，2，3}，V₂={1，2，3，4，5，6}.由定义3可知，该图序列是序列连通的，且T=2.

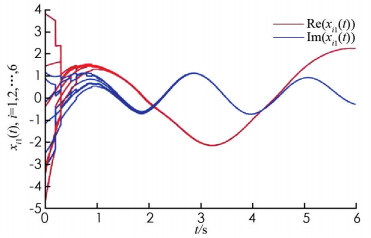
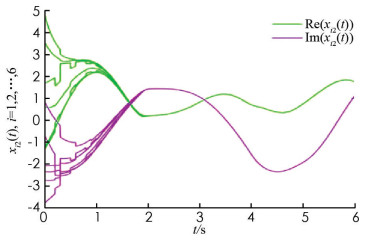
显然，$\alpha \left({{t_{2k - 1}}} \right) = \mathop {\min }\limits_{1 \le i \le 6} \left\{ {\sum\limits_{j \in {V_1}} {\rm{ }} {{\tilde \omega }_{ij}}\left({{t_{2k - 1}}} \right)} \right\} = 0.3, \alpha \left({{t_{2k}}} \right) = \mathop {\min }\limits_{1 \le i \le 6} \left\{ {\sum\limits_{j \in {V_2}} {\rm{ }} {{\tilde \omega }_{ij}}\left({{t_{2k}}} \right)} \right\} = 0.3$.通过计算，$\mathscr{L}$=0.7，$\tilde \delta $=0.464 1.对任意的k∈$\mathbb{Z}$⁺，取0 < t_k－t_k－1≤0.2=γ，那么$\left({1 - \prod_{s = 1}^T \alpha \left({{t_s}} \right)} \right) \times {{\rm{e}}^{\frac{{\tilde \delta }}{2}\gamma T}} = 0.7822 < 1$. 由定理1可知，耦合网络式(8)是全局渐近同步的，同步模拟结果如图 3和图 4所示.

本文研究了由复值神经网络通过脉冲耦合构成的复杂动态网络的渐近同步问题. 不同于以往的连续耦合机制，该网络节点仅在脉冲时刻进行信息交换和拓扑结构的切换. 在序列连通条件下，基于直接误差法及迭代的思想建立了脉冲耦合复值神经网络渐近同步的判定条件. 结果表明在网络耦合中出现不连续通讯时，对节点通讯进行适当地限制也能实现网络的渐近同步. 在以后的工作中，将探讨在脉冲耦合机制下具有随机切换拓扑的脉冲耦合网络的同步问题.