-
随着信息时代的高速发展,大数据成为这个时代最具代表性的标志之一. 如何在规模庞大、结构复杂的高维数据中挖掘出最有价值的信息是研究人员和技术工作的热点关注问题. 特征选择是一种有效的高维数据预处理方法,旨在去除数据中的冗余和不相关信息,降低数据维度和学习算法的计算复杂度,是人工智能基础理论中的热点研究主题.
特征选择[1]可分为嵌入式、封装式和过滤式等诸多方法. 嵌入式特征选择[2]将特征选择与学习器融合,在学习器训练过程中自动地进行特征选择. 该方法缺乏特征选择的可解释性. 封装式特征选择[3]通过从初始特征集合中不断地选择特征子集和训练学习器,根据学习器的性能来对子集进行评价,直到选择出最佳的子集. 多次训练学习器导致封装式特征选择方法的计算复杂度很高. 过滤式方法[4]通过设计特征评估度量或相关统计量,通过阈值法或启发式搜索方法选出具有代表性的特征. 常用的特征评估度量有熵、互信息、信息增益、基尼系数等等. 基于粗糙集[5]、邻域粗糙集[6]和模糊邻域粗糙集[7]的特征选择方法是一类重要的启发式特征选择方法,通过设计具有良好性质的特征评价函数,确保选出的特征子集保持甚至超过原始特征的分类能力,因而得以广泛研究.
启发式特征选择方法需要多次遍历所有候选特征,一些与分类无关或对分类不产生影响的冗余特征可能会被反复计算,在数据维度很高的情况下消耗大量的计算资源. 鉴于此,基于特征聚类的特征选择方法应运而生. 该类方法的主旨思想是通过构建描述数据特征间相似性和关联性的度量,采用某种聚类方法对特征聚类,并在各类簇中选择有代表性的特征作为特征选择子集. 文献[8]利用余弦函数刻画特征向量之间的相似性,采用K-均值对特征聚类,选择每一簇的中心特征构成特征子集. 该方法在特征聚类时仅考虑到特征间的相似性,缺乏特征与决策间的依赖关系,不能确保选出的特征子集具有独立性和最强的辨识能力. 文献[9]基于熵和信息增益概念构建集合间不确定性度量,描述特征间的相关性和特征与决策间的关联性,删除不确定度小于某一阈值的特征,构建以剩余特征为顶点、以特征间的不确定度为边权的最小生成树,通过阈值法获得特征的簇结构,并在每个簇中选择一个与决策关联性最大的特征作为特征选择的特征子集. 该方法既考虑了特征间的相关性,也分析了特征与决策间的关联性,但缺少特征集与决策间的依赖性以及特征集中元素的冗余性等方面的探索.
针对上述现有特征聚类驱动的特征选择存在的缺陷,本文提出一种决策依赖聚类的高维数据特征选择方法. 首先,在邻域粗糙集模型基础上分析了决策关于特征对的依赖度与决策关于单一特征的依赖度间的关系,构建了特征冗余度度量和特征冗余图,依据图割理论获得特征划分子集. 为了获得最优的特征分割,提出了一种簇内特征冗余度最大、簇间特征冗余度最小的聚类簇数评估方法. 通过分析聚类簇中特征关于决策的互信息及特征依存度度量,提出一种中心度和依存度联合的特征子集确定策略,实现高维数据的特征选择.
全文HTML
-
基于聚类思想的特征选择方法是通过构建数据特征间相似性度量,采用K-均值[10]或其他聚类方法将特征划分为不相交的子簇. 现有大部分方法在构建特征相似图时只考虑特征间的相似性,忽略数据的标签信息,导致数据特征与其对应决策类之间缺乏必要的关联性.
本节将基于邻域粗糙集理论构建一种决策依赖的特征聚类方法. 在回顾邻域粗糙集及相关概念基础上,提出一种基于决策依赖度的邻域依赖度增益的构造方法,并探讨了其性质. 基于特征间邻域依赖度度量构建特征相似图,采用谱聚类方法获得特征的类簇结构. 为了获得特征的最优聚类簇数,我们结合簇内冗余度和簇间冗余度给出一种最优特征簇的选择方法.
-
设DIS=〈U,A,V,D〉为一个决策信息系统,其中U={x1,x2,…,xn}为非空论域,A={a1,a2,…,am}为条件属性集,也称特征集,V是对象关于属性的(实数)值集,D为决策属性. 对∀x∈U,B⊆A,x由B确定的δ邻域信息粒[6]为
其中:δ(δ>0)为邻域参数,
${d_B}(x, y) = \mathop {\min }\limits_{{a_i} \in B} \left| {v\left({x, {a_i}} \right) - v\left({y, {a_i}} \right)} \right|$ 为对象x,y∈U关于属性集B的距离函数,v(x,ai)表示x在属性ai下的取值.对任意X⊆U,B⊆A和δ>0,X的关于B的δ下近似和δ上近似[6]分别定义为
下近似可以理解为由邻域信息粒完全包含在X中的对象构成,上近似包含邻域信息粒可能属于X的对象全体. 在知识发现中,上近似和下近似被用于对集合X做逼近描述.
在决策信息系统DIS=〈U,A,V,D〉中,记U关于决策属性集D的划分为U/D={D1,D2,…,DM},则对任意B⊆A和δ>0,决策属性集D的关于B的δ上近似、下近似和边界[11]可分别表示为
决策属性集D关于条件属性子集B的δ正域和依赖度[11]分别定义为
其中:|P|表示集合P的基数. 显然,D关于B的依赖度γBδ(D)是一个不大于1的非负实数. 如果γBδ(D)=1,则D完全依赖于知识B,也就是说,U关于属性集B的δ邻域覆盖是U关于决策D的划分的子覆盖;如果γBδ(D)=0,则D完全独立于B.
-
依赖度反映的是决策属性与条件属性间的依赖关系. 为了探讨属性对间的关系及其对决策产生的影响,本文构建决策依赖属性(特征)间的相似度度量. 该度量既描述决策属性与特征对的依赖性,又刻画特征间的关联性和相似性.
定义1 给定一个决策信息系统DIS=〈U,A,V,D〉,δ>0,对任意ai,aj∈A,简记γ{aj}δ(D)为γajδ(D),称
为特征ai和aj的平均邻域依赖度增益.
根据定义1,γ(ai,aj)δ(D)表示论域U被ai,aj粒化时,δ邻域信息粒被决策D完全正确认识的比例;γaiδ(D)和γajδ(D)分别表示用ai和aj单独粒化U时,对象能够被正确辨识的比例;Γ(ai,aj)δ(D)表示特征ai,aj同时被用于决策时,相对二者单独被用于决策时,被正确辨识的样本比例差值.
性质1 Γ(ai,aj)δ(D)=Γ(aj,ai)δ(D).
证明:显然.
性质2 0≤Γ(ai,aj)δ(D)≤1.
证明:对任意δ>0,ai,aj∈A,对象集U关于{ai,aj}的邻域粒化都是U分别关于ai和aj邻域粒化的子覆盖. 这样,POS{ai}δ(D)⊆POS{ai,aj}δ(D),POS{aj}δ(D)⊆POS{ai,aj}δ(D). 于是,0≤γaiδ(D)≤γ(ai,aj)δ(D)≤1,0≤γajδ(D)≤γ(ai,aj)δ(D)≤1,所以0≤2γ(ai,aj)δ(D)-γaiδ(D)-γajδ(D)≤2,因此,0≤Γ(ai,aj)δ(D)≤1.
性质3 Γ(ai,aj)δ(D)=0当且仅当γ(ai,aj)δ(D)=γaiδ(D)=γajδ(D).
证明:由定义1可知,Γ(ai,aj)δ(D)=0当且仅当2γ(ai,aj)δ(D)=γaiδ(D)+γajδ(D). 由于γaiδ(D)≤γ(ai,aj)δ(D)且γajδ(D)≤γ(ai,aj)δ(D),所以,γ(ai,aj)δ(D)=γaiδ(D)=γajδ(D).
性质3表明:特征ai,aj以及二者的联合{ai,aj}产生的邻域信息粒关于决策的认识是相同的(下近似相同). 在这种情况下,两个特征存在冗余性,最多仅需一个特征即可刻画对象的决策特性.
显然,Γ(ai,ai)δ(D)=0. 该结论表明,同一特征多次联合与独立用于刻画对象的决策是相同的. 从性质2的证明可知,平均联合依赖度增益关于特征数量是单调递增的. 因此,下面性质成立.
性质4 Γ(ai,aj)δ(D)=1当且仅当γ(ai,aj)δ(D)=1且γaiδ(D)=γajδ(D)=0.
根据性质4,如果Γ(ai,aj)δ(D)=1,则决策D独立于特征ai和aj中的任何一个,即论域U中的每个对象都不能被特征ai或aj有效辨识. 然而,决策D完全依赖这两个特征的联合. 也就是说,在论域被特征集{ai,aj}做邻域粒化后,每个对象关于决策D都可以被辨识. 这一事实表明:特征ai和aj是独立的,它们对辨识对象均是必要的.
-
基于1.2节的分析,如果两个特征的联合依赖度增益低,该特征对具有高的冗余度. 反之,如果其联合依赖度增益越高,则特征对决策分类越是必要的,且这两个特征的冗余性越低. 鉴于此,本文构建特征冗余图,并借助图割理论对特征做划分,形成特征冗余簇.
定义2 给定一个决策信息系统DIS=〈U,A,V,D〉,δ>0,记W=(wij)m×m,其中
称W为特征冗余度矩阵.
显然,W是一个相似矩阵,也可修正W,将其对角线元素全赋值为0,表明特征和自身不存在冗余性问题.在后续的特征冗余图图割划分中,特征冗余度矩阵修正与否对后续结果没有实质影响. 将特征集A中的元素作为顶点,将任意两个特征间的冗余度wij作为对应顶点间的边权值,形成一个特征冗余图G. 该图是一个加权无向图.
假设将特征冗余图G划分成k个连通子图A1,A2,…,Ak,构建图割损失函数[12]
其中
$cut(A, B) = \sum\limits_{i \in A, j \in B} {{w_{ij}}} $ . 使损失函数(3)达到最小的图割就是最优特征聚类.设称H=(hij)m×k为指标矩阵,其满足H′H=Ik×k. 这样,(3)式可转化为如下的矩阵形式
其中L=Λ-W,称之为图G的拉普拉斯矩阵,Λ为对角矩阵,其对角线元素分别为冗余度矩阵W对应的行元素之和.
求解(3)式或(4)式的极小值问题是一个NP难问题. 将损失函数(4)连续化,根据Rayleigh-Ritz定理[13],目标函数(4)的最优解H为L的前k个最小非零特征值对应的特征向量按列组成的矩阵.
矩阵H的每个列向量实质上就是图G顶点被分割后的簇标. 为了获取明确的簇标特征,采用常用的K-均值聚类方法对矩阵H的行向量聚类. K-均值聚类结果代表了特征的类簇结构.
-
由于K-均值聚类方法需要事先给定类簇数,但数据特征的类簇数并不明确. 为了获得特征的最优聚类结果,引入一种特征聚类簇数的评估度量方法指导特征类簇数的选取.
假设特征集A的聚类结果为FC={A1,A2,…,Ak},其中Ai={ai1,ai2,…,ai|Ai|}为A的第i簇特征集,称
为Ai的簇内平均冗余度;称
为两个特征簇Ai={ai1,ai2,…,ai|Ai|}和Aj={aj1,aj2,…,aj|Aj|}的簇间平均冗余度.
最优聚类结果应具有簇内特征冗余度最大而簇间特征最不相关的特点,也即簇内平均冗余度最大而簇间平均冗余度最小. 因此,构造如下最优类簇结构评估指标:
最优类簇结构评估指标依赖于聚类方法的不同,也取决于类簇数的选取. 评估指标值Cindex(k)越小,说明簇内的冗余性越大,簇间的冗余性越小,聚类效果越好. 因此,使式(7)达到最小的正整数k′就是特征的最优划分簇数,对应的划分簇是FC={A1,A2,…,Ak′}.
1.1. 邻域粗糙集基本概念
1.2. 决策依赖特征关联性度量
1.3. 基于冗余度的特征聚类
1.4. 最优特征簇结构
-
在特征聚类基础上,本节将探讨簇内特征选择策略. 互信息是度量两个随机变量间相关性的重要指标[14];本文提出一种基于互信息的簇内特征选择方法.
假设特征集A的聚类结果为FC={A1,A2,…,Ak},对任意特征ai∈A,存在唯一类簇Aj,使得ai∈Aj,称
为特征ai的依存度.
特征的依存度表示该特征与其簇内其他特征的平均冗余度. 特别地,如果某一特征簇中仅有一个元素,则该元素的依存度为0.
设对象集关于决策属性D的划分为U/D={D1,D2,…,DM},对任意特征ai∈A,存在唯一类簇Aj,使得ai∈Aj,ai关于决策D的互信息可表示为
其中:
$P\left({R_{\{ ai\} }^\delta (x)} \right) = \frac{{\left| {R_{\left\{ {{a_i}} \right\}}^\delta (x)} \right|}}{{|U|}}, P\left({{D_t}} \right) = \frac{{\left| {{D_t}} \right|}}{{|U|}}, P\left({R_{\left\{ {{a_i}} \right\}}^\delta (x), {D_t}} \right) = \frac{{\left| {R_{\left\{ {{a_i}} \right\}}^\delta (x) \cap {D_t}} \right|}}{{|U|}}.$ 从式(9)可以看出,如果特征ai诱导的邻域信息粒R{ai}δ(x)中绝大部分与相关决策等价类Dt都有较大交集,则ai关于决策D的互信息就大,此时,ai与决策更具相关性,ai的分类能力就很强. 特别地,如果对于任意x∈U都有R{ai}δ(x)=U则I(ai;D)=0,即ai关于决策D的互信息取得最小值0. 此时该特征没有任何分类能力. 由此可见,互信息I(ai;D)可以反映特征与决策之间的相关程度,互信息越大,特征与决策越相关,反之亦然.
对于任意特征簇Ai,设aij∈Ai是满足I(aij;D)=max k=1,2,…,|Ai| I(aik;D)的特征,则aij诱导的邻域信息粒包含在决策等价类中的整体程度最大. 因为簇内特征具有强冗余性,当簇内其余特征与aij共同粒化论域时,只能进一步细化邻域信息粒,对于邻域信息粒包含在决策等价类的整体程度越大的特征,细化能力越弱,该特征在簇内的整体依存度越大. 在这种情况下,特征aij在簇Ai中起着中心点的作用,称特征aij为对应簇Ai的中心特征,称互信息I(aij;D)为簇Ai的中心度.
中心特征是与决策具有最大互信息的特征,是该簇中最具代表性特征. 根据聚类思想,中心特征与该簇中其余特征间具有最大的冗余性. 另一方面,不同簇中的中心特征具有最小的冗余性和最大的独立性,而且,由于特征类簇是按照特征簇内冗余度最大、簇间冗余度最小确定的最优特征分割模式,将每个簇的中心特征作为特征选择子集是合理的,也是足够的. 简记这种特征选择方法为RDCFS.
下面我们以一个具体实例说明中心特征与其依存度和中心度间的关联性. 从UCI数据库中选取glass数据集,并从中随机抽取6个样本,如下表 1.
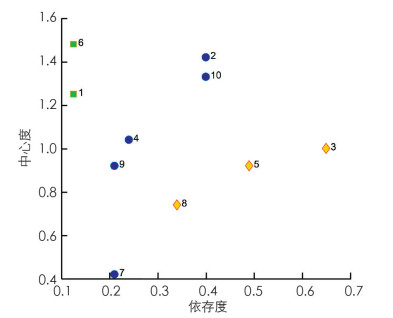
记其特征为A={a1,a2,…,a10},将数据归一化后,按照第1节方法得到特征聚类结果:A1={a1,a6},A2={a2,a4,a7,a9,a10},A3={a3,a5,a8}. 根据式(8)和(9)分别计算10个特征的依存度和中心度,见图 1. 在该图中,同一个类簇中的特征用同一种符号和相同颜色的点表示,不同簇中特征用不同符号和不同颜色表示.
从图 1可以看出,在同一个簇内,中心度越大的特征,在该簇内的依存度也越大,中心特征的依存度最大. 易见,a6,a2和a3的中心度和依存度在对应簇中最大,它们分别就是簇A1,A2和A3的中心特征. 因此,{a2,a3,a6}是A的最优特征选择子集.
综合上述分析,下面给出决策系统的基于决策依赖聚类的特征选择算法.
算法1 基于决策依赖聚类的特征选择算法(RDCFS) 输入:训练数据集IS=〈U,A,V,D〉,m为特征数,邻域参数δ,指定聚类个数范围Ξ; 输出:特征子集S. BEGIN 1.初始化被选特征子集S=Φ,全部特征集合为F; 2.for each k∈Ξ; //
Ξ:指定聚类个数范围3.基于公式(4)实现特征聚类; 4.计算公式(5),(6),(7); 5.end for 6.k′=arg mink Cindex(k); // 选出最优簇类数 7.FC={A1,A2,…,Ak′}; 8.for each Ai∈FC 9.for each ai∈Aj,计算中心度(9); 10. ${{\rm{b}}_{\rm{i}}} = \mathop {\arg \max }\limits_{{\rm{ai}} \in {{\rm{A}}_{\rm{j}}}} {\rm{I}}\left({{{\rm{a}}_{\rm{i}}}; {\rm{D}}} \right)$ ; // 选出每个簇内中心度最大的特征11. end for 12.end for 13.特征子集S={b1,b2,…,bk′}. END
-
为了验证本文提出的特征选择方法的合理性和有效性,从UCI数据库中选取8个数值型数据集,详细信息见表 2. 利用这8个数据集验证本文所提特征选择方法选出的特征子集在分类精度上的性能.
首先以表 2中前4个数据集为例验证根据式(7)选取聚类数的合理性. 实验采取十折交叉验证的方法.根据邻域粗糙集特征选择方法邻域参数的一般选取规则,本文中δ在区间[0.01,0.5]内取值. 给定类簇数的取值范围,以一定步长通过遍历方法得到使式(7)达到最小的聚类数目. 在聚类基础上,在每个簇内选择中心度最高的特征形成特征子集. 采用如下所述邻域投票精度作为特征选择有效性的度量指标.
设特征集A={a1,a2,…,am}的特征选择结果为S={ac1,ac2,…,ack},任意对象xi∈U关于特征子集S的δ邻域信息粒为RSδ(xi)={y∈U|dS(xi,y)≤δ},规定xi的准类别标签diδ为RSδ(xi)中对象的真实标签采用多数投票策略获得的标签,则邻域投票精度为
其中
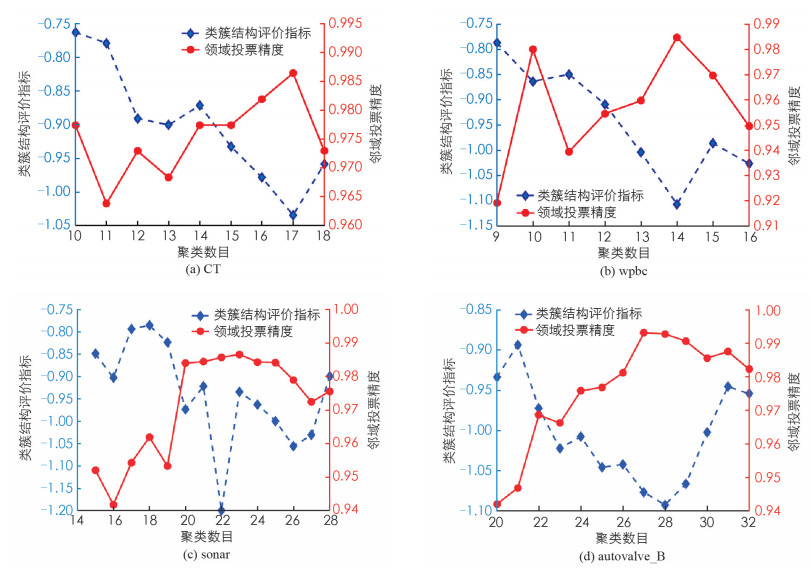
$\left|v\left(x_{i}, D\right)=d_{i}^{\delta}\right|=\left\{\begin{array}{ll}1, & v\left(x_{i}, D\right)=d_{i}^{\delta} \\ 0, & \text { 否则}\end{array}\right.$ ,v(xi,D)为xi的真实类别标签,v(xi,D)=diδ表示xi的真实类别标签与准类别标签相同.图 2绘出了表 2中前4个数据集特征对的不同聚类数目对应的类簇结构评价指标和邻域投票精度的变化情况. 其中不同线形、不同颜色分别代表数据的类簇结构评价指标和邻域投票精度的变化情况.
由图 2分析可知,给定一定的聚类数目范围:在CT和wpbc两个数据集上,类簇结构评价指标达到极小,即将特征分别聚成17类和14类时,邻域投票精度达到最高;在sonar和autovalve_B两个数据集的类簇结构评价指标达到极小时,所选特征的邻域投票精度达到次最高,且当聚类数目逐渐增加时,邻域投票精度呈现下降趋势. 这说明,我们构造的类簇结构评价指标能够驱动确定有效的聚类数目,从而促进特征选择的精度提高.
为了进一步验证本文提出方法的优势,分别与联合谱聚类与邻域互信息的特征选择算法(SCNMI)[15]、基于特征聚类的特征选择方法(FSFC)[16]、模糊粗糙测度特征选择(FRSE)[17]和模糊邻域粗糙集特征选择(FNRS)[7]4种特征选择方法在8个数据集上进行模拟实验比较. 表 3给出了5种特征选择方法对8个数据集做出的特征选择结果,其中的数值代表最终特征选择子集中的特征数.
从表 3可以看出,在8个数据集的实验中,本文所提方法(RDCDS)在7个数据集上都选出了最优(最小)特征子集,尤其对高维数据集具有更好的降维作用.
为了验证特征子集的分类能力,分别采用KNN分类器(本文取K=3)和支持向量机分类器(SVM)对数据集在特征选择前后的分类效果进行了对比实验,各个方法在不同数据集上的分类精度如表 4和表 5所示.
从表 4和表 5可以看出,不论采用KNN分类器还是SVM分类器,在8个数据集的实验中本文所提方法(RDCDS)在5个数据集上取得了最高的分类精度. FNRS在2个数据集上取得了最高KNN分类精度,FSFC只在一个数据集上取得最高KNN分类精度,而SCNMI和FRSE表现最差. 同时,FSFC,FRSE和FNRS分别仅在一个数据集上取得最高的SVM分类精度,SCNMI依然表现最差.
尽管如此,特征选择后的数据分类精度都高于原始数据的分类精度. 这一事实说明原始数据包含冗余和不相关信息,扰乱了对数据的分类学习,进一步证实特征选择的必要性. 上述对比实验表明,从统计学意义上讲,本文提出的特征选择方法得到的特征子集不仅紧凑,数据分类精度还得以显著提高.
-
本文基于邻域粗糙集模型建立了一种特征聚类驱动的特征选择方法. 该方法不同于现有启发式特征选择和基于特征聚类的特征选择,从特征依赖度出发构建了特征冗余图,给出了最优特征冗余图聚类准则和聚类方法. 在此基础上,通过引入簇内特征依存度和中心度的概念,给出了特征依赖聚类的特征选择算法. 理论分析和多个数据集上的对比实验结果表明新提出的特征选择方法不仅可以选出特征数更小的特征子集,其对应的分类精度还得以提高.
本文中最优特征簇结构的评估指标通过遍历方式得到,探索一种特征类簇数自适应确定方法是很有意义的. 通过分析特征与特征间的因果关联,基于有向特征图图割的特征选择方法是一个值得深入研究的问题.



 下载:
下载: