对(1+1)维非线性时间分数阶Klein-Gordon方程(1)做如下的分数复变换^[15]

其中l，λ是任意非零常数，Γ为伽马函数，则可将方程(1)转化为方程

其中$u_{\xi \xi}=\frac{\partial^{2} u}{\partial \xi^{2}}$. 下面对方程(3)进行定性分析. 假设u_ξ=y，方程(3)等价于如下平面动力系统

对系统(4)进行首次积分

再令

可得u₁=0，u_2，3=±$\sqrt{-\frac{\beta}{\gamma}}$(其中${\frac{\beta}{\gamma}}$ < 0). 从而当${\frac{\beta}{\gamma}}$≥0时，系统(4)只有1个平衡点(u₁，0). 当${\frac{\beta}{\gamma}}$ < 0时，系统(4)有平衡点(u₁，0)与(u_2，3，0)，在平衡点(u_i，0)，i=1，2，3处的Jacobi矩阵行列式为

根据平面动力系统理论^[16-17]可知，如果J(u_i，0) < 0则为鞍点，如果J(u_i，0)>0则为中心，如果J(u_i，0)=0则为尖点，因此对于系统(4)有：

1) 当βγ < 0，λ²-l²>0时，将平衡点(u₁，0)，(u_2，3，0)代入(7)式知J(u₁，0)=-$\frac{\beta}{\lambda^{2}-l^{2}}$，J(u_2，3，0)=$\frac{2\beta}{\lambda^{2}-l^{2}}$，从而可知：平衡点(u₁，0)在β>0时为鞍点，在β < 0时为中心；平衡点(u_2，3，0)在β>0时为中心，在β < 0时为鞍点.

2) 当βγ≥0，λ²-l²>0时，将平衡点(u₁，0)代入(7)式知J(u₁，0)=-$\frac{\beta}{\lambda^{2}-l^{2}}$，从而可知平衡点(u₁，0)在β>0时为鞍点，在β < 0时为中心.

3) 当βγ < 0，λ²-l² < 0时，平衡点(u₁，0)，(u_2，3，0)对应的Jacobi矩阵行列式分别为

从而可知平衡点(u₁，0)在β>0时为中心，在β < 0时为鞍点；平衡点(u_2，3，0)在β>0时为鞍点，在β < 0时为中心.

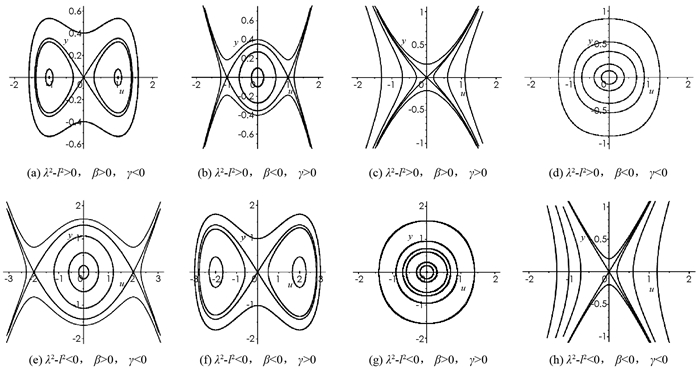
4) 当βγ≥0，λ²-l² < 0时，平衡点u₁(0，0)对应的Jacobi矩阵行列式为J(u₁，0)=-$\frac{\beta}{\lambda^{2}-l^{2}}$，从而可知平衡点(u₁，0)在β>0时为中心，在β < 0时为鞍点.

根据上面的奇点分析，利用Maple软件画出系统(4)在不同参数条件下的相图见图 1.

由平面动力系统理论与方法^[16-17]可知，同宿轨对应着方程(3)的钟状孤波解，异宿轨对应着方程(3)的扭状孤波解，闭轨对应着方程(3)的周期解. 因此根据相图 1中的(a)-(h)，可得出方程(3)的有界行波解的个数及存在性结论为：

1) 系统(4)在λ²-l²>0，β>0，γ < 0时存在两条同宿轨，无穷多个闭轨，从而方程(3)存在两个钟状孤波解和无穷多个周期解(图 1(a)).

2) 系统(4)在λ²-l²>0，β < 0，γ>0时存在两条异宿轨，无穷多个闭轨，从而方程(3)存在两个扭状孤波解和无穷多个周期解(图 1(b)).

3) 系统(4)在λ²-l²>0，β>0，γ>0时不存在闭轨(图 1(c)).

4) 系统(4)在λ²-l²>0，β < 0，γ < 0时存在无穷多个闭轨，从而方程(3)存在无穷多个周期解(图 1(d)).

5) 系统(4)在λ²-l² < 0，β>0，γ < 0时存在两条异宿轨，无穷多个闭轨，从而方程(3)存在两个扭状孤波解和无穷多个周期解(图 1(e)).

6) 系统(4)在λ²-l² < 0，β < 0，γ>0时存在两条同宿轨，无穷多个闭轨，从而方程(3)存在两个钟状孤波解和无穷多个周期解(图 1(f)).

7) 系统(4)在λ²-l² < 0，β>0，γ>0时存在无穷多个闭轨，从而方程(3)存在无穷多个周期解(图 1(g)).

8) 系统(4)在λ²-l² < 0，β < 0，γ < 0时不存在闭轨(图 1(h)).

由上面的定性分析可知，方程(3)存在4个钟状孤波解、4个扭状孤波解和无穷多个周期波解，下面运用辅助方程法讨论方程(1)的一些有界行波解的精确表达式.

运用辅助方程法求解非线性发展方程的精确解是十分有效的，本文运用的辅助方程法是Khater博士在2018年所提出并改进的，辅助方程法的具体步骤如下^[9-10]：

考虑如下的非线性偏微分方程：

其中u(x，t)是未知函数，且P是包含u(x，t)及其各导数的多项式函数.

步骤1：对方程(8)做行波变换u(x，t)=u(ξ)，ξ=lx-λt，其中l，λ是任意非零常数，即方程(8)可化为如下的常微分方程：

其中$\left(\frac{\mathrm{d} u}{\mathrm{~d} \xi}=u^{\prime}, \frac{\mathrm{d}^{2} u}{\mathrm{~d} \xi^{2}}=u^{\prime \prime}, \cdots\right)$，F是包含u(x，t)及其各导数的多项式函数.

步骤2：假设常微分方程(9)的解具有如下形式：

其中a_i，b_i(i=0，1，2，…，n)为待定系数，n由齐次平衡原则确定，f(ξ)满足如下常微分方程

其中α，ϑ，δ，a是非零常数且a>0，a≠1.

步骤3：将方程(10)，(11)代入方程(9)，合并a^±if(ξ)，i=0，1，2，…，n的各次幂系数，并令各次幂系数等于零，得到关于a₀，a_i，b_i，l，λ(i=1，2，…，n)的代数方程组，结合Maple软件求解代数方程组，可得a₀，a_i，b_i，l，λ(i=1，2，…，n)的值.

步骤4：通过方程(11)的解和步骤3的值，由假设(10)得出方程(9)的解，进而可获得方程(8)行波解的精确表达式.

方程(11)的解有如下3种情形：

情形1：如果ϑ²-4αδ>0且δ≠0，那么有

情形2：如果ϑ²-4αδ < 0且δ≠0，那么有

情形3：如果ϑ²=4αδ且δ≠0，那么有

下面利用辅助方程法来讨论方程(1)的有界行波解，通过该方法得出了方程(1)的两组不同参数的解，则具体根据方程(3)的最高阶导数项u″(ξ)与最高阶非线性项u³(ξ)的平衡原则，有n+2=3n得n=1，根据上述方法可设方程(3)的解具有如下形式：

其中：a₀，a₁，b₁为待定系数；将方程(15)及其导数代入方程(3)，合并a^±if(ξ)，i=0，1，2，3的各次幂，并令各次幂的系数等于零，得到关于a₀，a₁，b₁，l，λ的代数方程组为：

结合Maple软件求解方程组(16)，得出以下两种情形.

情形1：

其中l为任意非零常数.

情形2：

其中l为任意非零常数.

由(15)，(17)式与方程(11)的解(13)、分数复变换(2)可得方程(1)的有界行波解为：

其中ϑ²-4αδ < 0且δ≠0，l为任意非零常数.

由(15)，(17)式与方程(11)的解(12)、分数复变换(2)可得方程(1)的有界行波解为：

其中ϑ²-4αδ>0且δ≠0，l为任意非零常数.

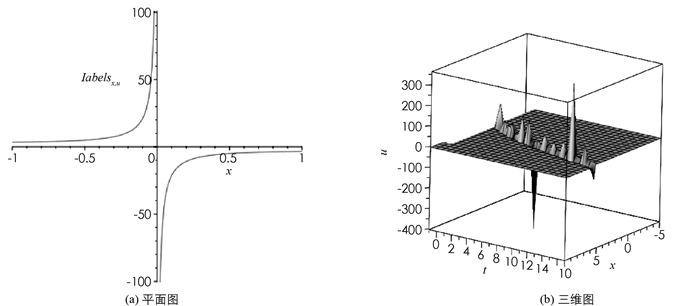
进而可得解(19)，(20)为周期解，且在β < 0时对应系统(4)的相图 1(b)的闭轨，在β>0时对应系统(4)的相图 1(e)的闭轨；解(21)，(22)为扭状孤波解，且解(21)在β < 0时对应系统(4)的相图 1(b)的两条异宿轨，解(22)在β>0时对应系统(4)的相图 1(e)中的两条异宿轨. 取α=2，ϑ=-3，γ=$\frac{1}{5}$，l=3，λ=$\sqrt{13}$，β=-2，δ=1，θ=$\frac{1}{2}$，运用Maple软件给出u₇的平面图和三维图见图 2.

由(15)，(18)式与方程(11)的解(13)、分数复变换(2)可得方程(1)的有界行波解为

其中ϑ²-4αδ < 0且δ≠0，l为任意非零常数.

由(15)，(18)式与方程(11)的解(12)、分数复变换(2)可得方程(1)的有界行波解为

其中ϑ²-4αδ>0且δ≠0，l为任意非零常数.

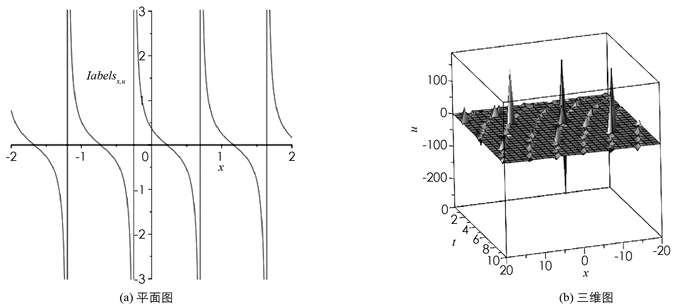
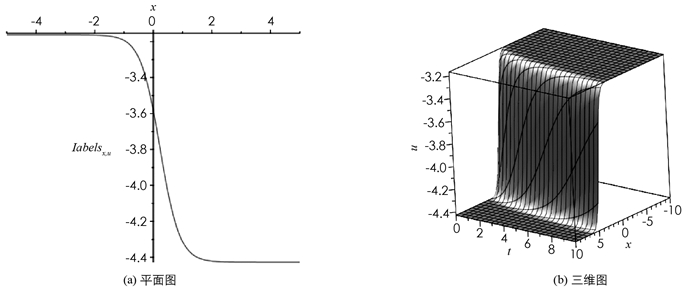
由上述解知：解(23)，(24)为周期解，在β < 0时对应系统(4)的相图 1(b)中的闭轨，在β>0时对应系统(4)的相图 1(e)中的闭轨；解(25)，(26)为扭状孤波解，解(25)在β < 0时对应系统(4)的相图 1(b)的两条异宿轨，解(26)在β>0时对应系统(4)的相图 1(e)中的两条异宿轨. 取α=5，ϑ=3，γ=-6，l=-2，λ=$\sqrt{\frac{42}{11}}$，β=-1，δ=1，θ=$\frac{1}{2}$时运用Maple软件给出u₁₁的平面图和三维图见图 3；取α=2，ϑ=-3，γ=5，l=3，λ=-$\sqrt{13}$，β=-2，δ=1，θ=$\frac{1}{2}$时运用Maple软件给出u₁₄的平面图和三维图见图 4.

注1  解(25)与解(21) 分别是图 1(b)中的两条异宿轨对应的扭状孤波解的两种不同表达式，解(26)与解(22)分别是图 1(e)中的两条异宿轨对应的扭状孤波解的两种不同表达式.

本文利用平面动力系统理论与方法以及辅助方程法，讨论了非线性时间分数阶Klein-Gordon方程有界行波解的存在性及精确表达式，其中包括双曲函数解、三角函数解；由定性结论可知方程(1)还存在4个钟状孤波解和无穷多个周期解，在此用辅助方程法还没能给出其精确表达式.