-
图的标号来源于1967年Rosa提出的优美树猜想,它的出现使得很多生活中的实际问题得到解决,如优美图可应用在密码设计、通讯网络编址、交通物流控制、雷达脉冲编码及X射线密码技术等[1-4]. 由于图形能够直观有效地解决实际生活中的一些难以解决的问题,所以衍生了图论的一系列应用. 因此,研究图的标号不仅能丰富图论的研究成果,而且能更广泛地应用于实际生活中的问题.
文献[4]提出了顶点魔幻全标号,之后该标号被越来越多的学者关注和研究. 通过文献[4-9]可知,在满足一定的条件下,特殊图圈图Cn、路图Pn,Km,m,Km,m-e以及Kn存在顶点魔幻全标号. 该标号的研究成果主要集中在特殊图,针对一般图的结果较少,研究方法绝大多数都是传统方法,利用计算机算法来研究的文献非常少见.
太阳图常被用来刻画环形网络,该网络在网络设计、网络建设中有着重要应用,标号理论是研究环形网络的方法之一. 文献[7]指出图G-sunG*在
$e>\left(-1+\sqrt{1+8 n^{2}}\right) / 2$ 时不存在顶点魔幻全标号,其中图G是任意n阶图. 文献[10-11]给出了当n≥3且1≤m≤$\lfloor(n+1) / 2\rfloor$ 时,图p(n,m)存在魔幻常数k=9n+2,10n+2,11n+2的顶点魔幻全标号. 通过文献[12]可知,太阳图存在{a,d}-点反魔幻边标号,其中d={1,4}.本文利用顶点魔幻全标号优化算法得到有限点内的随机图标号,进一步研究太阳图Sn,GSn,Sn,m以及图P(n,1)的顶点魔幻全标号. 通过分析算法结果,发现上述几类太阳图的标号特性,总结出若干定理并给出证明.
全文HTML
-
图G(p,q)表示的是包含p个顶点,q条边,且顶点集合为V(G),边集合为E(G)的简单连通图. 顶点v的度记为d(v);Cn指的是n个顶点的圈图.
定义1[3] 对于给定的图G(p,q),如果存在常数k和一一映射f:V(G)∪E(G)→{1,2,…,p+q},使得对每个顶点v∈V(G)都满足
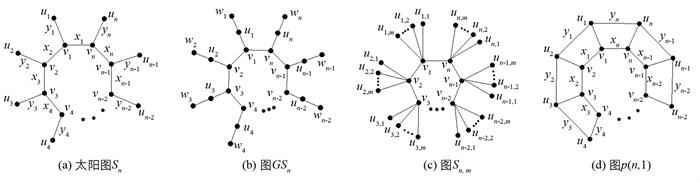
$f(v)+\sum\limits_{u \in N(v)} f(u v)=k$ ,其中N(v)表示与顶点v所关联的顶点的集合,k为魔幻常数,则称f是图G(p,q)的顶点魔幻全标号(vertex-magic total la b eling),简称VMTL图.定义2[3] 太阳图Sn是由n个顶点的Cn和n片叶子组成,其中Cn的每一顶点只能与一片叶子邻接,如图 1(a)所示. 在太阳图Sn的每一个叶子节点悬挂一个点构成的图记为图GSn,如图 1(b)所示.
定义3 [3] Cn的每个顶点vi(i∈{1,2,…,n})连接m个顶点ui(i∈{1,2,…,m})所构成的图记为图Sn,m,如图 1(c)所示.
定义4[3] 将太阳图Sn的每个叶子相连构成的图记为图p(n,1),如图 1(d)所示.
顶点魔幻全标号算法基于解空间的递归搜索算法,为了方便介绍算法步骤,下面给出优化前的解空间的定义.
定义5 对于度序列{d(vi)}(i=1,2,…,p),相同的一类图G(p,q)都存在一个表(如表 1),设u,v∈V(G),uv∈E(G),映射f:V(G)∪E(G)→{1,2,…,p+q},满足f(v),f(uv)∈[1,p+q],
$f(v)+\sum\limits_{u \in N(v)} f(u v)=k$ ,其中N(v)指顶点v的关联点,则称表 1为图G(p,q)的VMTL解空间.
-
对于图G,当图G满足VMTL时,存在映射:f:V(G)∪E(G)→{1,2,…,p+q},即所有的标号总和C为
其中,Sp和Sq分别表示顶点和边的标号值总和.
图G的每个顶点满足
当图G满足VMTL时,魔幻常数k的取值范围为
根据公式(1)及定义5实现VMTL算法,并在算法中增加判断函数对解空间进行优化,删除不满足判断函数条件的解空间,减少算法的时间复杂度,判断函数如公式(2)所示:
其中优化算法为
解空间优化算法 Requre 初始化解空间,图G的度序列及相同d(v)的个数 Repeat 从训练集解空间中选择标号值样本{(1,k-1),(2,k-2),…,(p+q,k-p+q)}; 参数更新|d(vi)+1| ←符合条件的样本个数 Until 样本集筛选完成 顶点魔幻全标号优化算法实现的主要思路如下:
(i) 由文献[12]中的非同构图算法生成有限点内的所有非同构图;
(ii) 获取图G的度序列、魔幻常数,同时结合定义5得到解空间;
(iii) 利用解空间优化算法对解空间进行优化,将不可用的解空间删除;
(iv) 搜索解空间得到满足条件的标号值.
顶点魔幻全标号优化算法实现如下:
VMTL算法 Input 图G(p,q)的邻接矩阵 Output 标号结果 Begin 1. C ←(p+q)(p+q+1)/2 2. for i ← 1 to p+q 3. k ← (i+C)/p 4. 利用算法1得到当前k值下的解空间φ(p,q,k) 5. if(|φ| < p) 6. continue; 7. else 8. Search for a combination of labels φ(p,q) 9. if φ(p,q) satisfies the VMTL conditions 10. return VMTL matrix 11. end if 12. end Search 13. end if 14. end for 15. if(图G存在VMTL) 16. output(VMTL结果矩阵) 17. else 18. output(输出该图的邻接矩阵) 19. end if End
-
利用算法得到了图Sn,GSn,Sn,m及图P(n,1)(3≤n≤6)的VMTL标号,经过分析得到以下标号结论:
定理1 对于太阳图Sn,当n≥3时存在魔幻常数k=5n+3的顶点魔幻全标号.
证 太阳图Sn的顶点集合
边集合为
即
对于太阳图Sn(n≥3),根据算法执行结果,分析得到该图存在以下标号:
太阳图Sn的顶点和边标号集合分别为
由f(vi)和f(ui)的标号可知f(vi)和f(ui)两两互不相交,且为顶点集f(v)到数集{n,n+2,2n+2,2n+3,2n+4,…,3n,3n+2,3n+3,…,4n}的一一映射. 同理,f(xi)和f(yi)两两互不相交,且为边集f(e)到数集{1,2,…,n-1,n+1,2n+1,2n,2n-1,…,n+3,3n+1}的一一映射. 则f(v)∪f(e)={1,2,…,4n},对于图中任意点vi,w为v1的关联点,魔幻常数k满足以下公式:
所以,f是太阳图Sn的顶点魔幻全标号,使得太阳图Sn为魔幻常数k=5n+3的顶点魔幻全标号图,即定理1成立. 以图S15为例,将标号结论应用到图标号中,得到图S15的VMTL标号如图 2(a)所示.
定理2 对于图GSn,当n≥3时存在魔幻常数k=8n+2的顶点魔幻全标号.
证 设图GSn的顶点集合为
边集合为
即
对于图GSn(n≥3),根据算法执行结果,分析得到该图存在以下标号:
对于图GSn,有
可知f(vi),f(ui)和f(uivi)两两互不相交,且为f1→{1,3,5,…,6n-1}的一一映射;f(wi),f(uiwi)和f(v1vn),f(vnvn-1),…,f(v2v1)为f2→{2,4,6,…,6n}的一一映射. 使得
对于图中任意点vi,k满足公式
即定理2成立,以图GS10为例,将标号结论应用到图标号中,得到图GS10的VMTL标号如图 2(b)所示.
定理3 广义太阳图Sn,m(n≥3,m>1)不存在顶点魔幻全标号.
证 由顶点魔幻全标号优化算法可知图Sn,m(n≥3,m≥2)不存在标号,即算法输出为图的邻接矩阵. 设图Sn,m(n≥3,m≥2)的顶点集合为
边集合为
如图 1(c)所示. 即|V|=n+mn,|E|=n+mn,如果图Sn,m存在顶点魔幻全标号,由定义1可知标号集合为
由图Sn,m可知
由文献[8]的定理5可以得到k取最小值时,图中d(v)=m+2的顶点及其关联边取标号集合{1,2,…,2n+mn},且顶点集合{v1,v2,…,vn}两顶点之间的关联边取标号集合{1,2,…,n}. k取最大值时,d(v)=2的顶点集合u={u1,1,u1,2,…,un,m}取标号值{2n+1,2n+2,…,2n+2mn}. 即
当图Sn,m满足顶点魔幻全标号时,有kmin≤kmax,结合公式(3)和(4),当图Sn,m存在顶点魔幻全标号时,n和m满足m2n+m-3n+1≤0. 通过分析可知,当n≥3,m=1时有解,该图为太阳图,其标号规律如定理1;而当n≥3,m>1时无解,因此不存在顶点魔幻全标号. 定理3成立.
定理4 对于图P(n,1),当n≥3时存在魔幻常数k=10n+1的顶点魔幻全标号.
证 设图P(n,1)的顶点集合为
边集合为
即V|P(n,1)|=2n,E|P(n,1)|=3n,所以f(v)∪f(e)={1,2,…,5n}. 对于图P(n,1)(n≥3),根据算法执行结果,分析得到该图存在以下标号:
对于图p(n,1),其顶点和边的集合分别为
f(vi)和f(ui)两两互不相交,且点标号为f(v)→{3,8,13,18,…,3+5(n-1),5,10,15,…,5n}的一一映射. f(xi)和f(yi)两两互不相交,且边标号为f(e)→{1,6,11,…,1+5(n-1),2,7,12,…,2+5(n-1),4,9,14,…,4+5(n-1)}的一一映射. 使得f(v)∪f(e)={1,2,…,5n},k满足公式
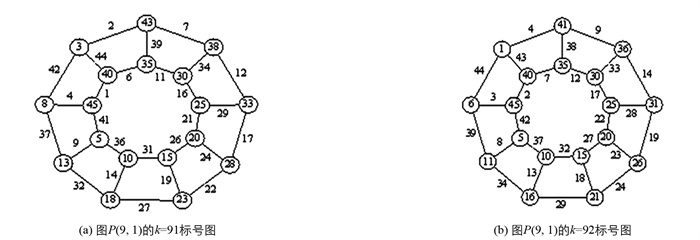
$k=f\left(v_{1}\right)+\sum\limits_{w \in N\left(v_{1}\right)} f\left(w v_{1}\right)=10 n+1$ .综上所述,定理4成立. 以图P(9,1)为例,由标号结论得到图P(9,1),k=91的VMTL标号如图 3(a)所示.
定理5 对于图P(n,1),当n≥3时存在魔幻常数k=10n+2的顶点魔幻全标号.
证 由定义理4可知图P(n,1)的f(v)∪f(e)={1,2,…,5n},由算法可知图P(n,1)(n≥3)存在以下标号:
同定理4,点标号为f(v)→{1,6,11,16,…,1+5(n-1),5,10,15,…,5n}的一一映射. 边集合为f(e)→{2,7,12,…,2+5(n-1),3,8,13,…,3+5(n-1),4,9,14,…,4+5(n-1)}的一一映射. 使得f(v)∪f(e)={1,2,…,5n},k满足公式
定理5成立. 以图P(9,1)为例,由标号结论得到图P(9,1),k=92的VMTL标号如图 3(b)所示.
-
本文利用VMTL算法得到有限点内的VMTL图集,通过对标号集合分析得到:太阳图Sn当n≥3时存在魔幻常数k=5n+3的顶点魔幻全标号;图GSn当n≥3时存在魔幻常数k=8n+2的顶点魔幻全标号;图P(n,1)当n≥3时存在魔幻常数k=10n+1和k=10n+2的顶点魔幻全标号. 同时得到广义太阳图Sn,m(n≥3,m≥2)不存在顶点魔幻全标号,并证明了结论的正确性.



 下载:
下载: