-
传染病是由各类病原体引起的能在人与人、动物与动物或者人与动物之间传播的一类疾病. 传染病的爆发可能会对人类的公共卫生安全和生命健康造成重大伤害,故传染病的监督防治一直是人类重视的工作内容. 数学动力学模型是用来分析传染病传播和控制问题的重要工具之一. 文献[1]将人群分为易感者(S)、感染者(I)、康复者(R),建立了著名的SIR仓室模型来研究传染病. 此后,仓室模型得到了广泛地研究[2-16]. 特别地,文献[2-4]考虑了医院治疗有限的因素,采用了以下不同的治疗函数:
或者
考虑到人口规模非恒定,且生存资源有限,用指数增长来描述人口增长不太符合实际情况. 基于此,文献[5, 11, 12]中的传染病模型里采用了非线性出生率函数. 文献[11]在没有疾病的情况下,假设人口增长的方程:
其中,d是死亡率常数,b(N)N是出生率函数,且b(N)必须满足3个条件:
(1) b(N)>0;
(2) b(N)是连续可微的,且b′(N) < 0;
(3) b(0+)>d>b(∞).
并提出b(N)可以采取的一种形式为:
$\bar{b}(N)=\frac{A}{N}+c, A>0, d>c>0$ .当传染病在传播时,自由活动的人群中会有患病者和易感者,病人中的一部分会去医院,患病者的另一部分在未察觉到自身患病时会感染他人. 所以,本文将人群分为易感者(S)、感染者(I)、住院者(H)、康复者(R). 传染病爆发时,由于医院的物资、空间、医护人员都是有限的,病人数目过多时,医院不可能接受全部病人. 另外,医院的医疗资源紧张程度也会对感染者是否选择去就医产生一定影响. 鉴于此,考虑非线性出生率
$\bar{b}(N)=\frac{A}{N}+B, (B < \mu)$ 和医院容纳量,建立了如下模型:其中:S(t),I(t),H(t),R(t)分别表示t时刻易感者、感染者、住院者以及康复者的数量,N表示总的人口数量,N=S+I+H+R,A表示人口输入数量,B和μ分别是出生率和自然死亡率,ε1和ε2分别是感染者与住院者的因病死亡率,β是感染率,γ1是感染者的自愈率,γ2是住院者的治愈率,r是已感染的人去医院就医的转移率,K表示医院所能收治的病人最大数目.
全文HTML
-
定理1 当初始值满足S(0)>0,I(0)>0,H(0)>0,R(0)>0时,模型(1)的解(S(t),I(t),H(t),R(t))对于任意t>0是正的且一致有界的.
证 首先证明对于任意的t>0,有I(t)>0. 由模型(1)的第二个方程可得
因此对于任意t>0,有I(t)>0.
再证明对于任意的t>0,H(t)>0成立. 否则,存在t1>0是使得H(t)=0成立的最小时刻. 因为H(0)>0,故当t∈[0,t1)时,有H(t)>0. 根据模型(1)的第三个方程,得
从而存在δ1>0,使得t∈(t1-δ1,t1),有H(t) < 0. 这与当t∈[0,t1)时,H(t)>0矛盾. 故对于任意的t>0,H(t)>0.
由模型(1)的第4个方程可得
由t>0,H(t)>0,I(t)>0可知,对于任意t>0,R(t)>0.
最后,证明对于任意t>0,S(t)>0成立. 否则,存在t2>0是使得S(t)=0成立的最小时刻. 因为S(0)>0,故当t∈[0,t2)时,有S(t)>0. 根据模型(1)的第一个方程有
故存在δ2>0,使得当t∈(t2-δ2,t2)时S(t) < 0. 这与当t∈[0,t2)时S(t)>0矛盾. 所以,对任意t>0,S(t)>0.
接下来证明解的一致有界性. 令N(t)=S(t)+I(t)+H(t)+R(t),由模型(1)可得
则有
即模型(1)的解是一致有界的.
由定理(1)可知,
$\mathbb{R}_{+}^{4}$ 的内部是关于模型(1)的正不变集. 类似地,也可证明$\mathbb{R}_{+}^{4}$ 是模型(1)的正不变集. 因此,我们可在可行域:内对模型(1)进行研究.
-
利用文献[6]中的下一代矩阵方法,计算出模型的基本再生数:
令模型(1)中右端的4个方程等于0,可得模型的无病平衡点:
$\boldsymbol{E}_{0}=\left(\frac{A}{\mu-B}, 0, 0, 0\right)$ 定理2 若R0 < 1,则模型(1)无病平衡点E0局部渐近稳定;若R0>1,则E0不稳定.
证 模型(1)在平衡点E0处的雅可比矩阵:
其特征方程:
特征根为
显然λ1,λ3,λ4都小于0,当R0 < 1时,λ2 < 0. 所以,若R0 < 1,无病平衡点E0局部渐近稳定.
当R0>1时,λ2>0,此时,E0不稳定.
定理3 当
$\frac{\beta A}{(\mu-B)\left(\mu+\varepsilon_{1}+\gamma_{1}\right)} < 1$ 时,E0全局渐近稳定.证 对V函数
沿着模型(1)的解轨线求导,得
在G内有
$S \leqslant \frac{A}{\mu-B}$ . 当$\frac{\beta A}{(\mu-B)\left(\mu+\varepsilon_{1}+\gamma_{1}\right)} < 1$ 时,$\frac{\mathrm{d} V}{\mathrm{~d} t} \leqslant 0. \frac{\mathrm{d} V}{\mathrm{~d} t}=0$ 当且仅当I=0,H=0. 所以,$\left\{(S, I, H, R) \in G \mid \frac{\mathrm{d} V}{\mathrm{~d} t}=0\right\}$ 的最大不变集是{E0}. 由LaSalle不变集原理[9]可知,E0全局渐近稳定.
-
令模型(1)右边的4个方程等于0,得
在方程组(2)中,通过计算可得
由方程组(2)中的第二个方程,可得
将上述S*,H*的表达式代入,得
合并计算,得到一个关于I*的一元二次方程
其中:
因为B<μ,所以
R0与M有如下等价关系
若R0>1,则有M>0,又由于p < 0,此时方程(3)必存在一个正根. 当R0=1时,M=0成立,由于p < 0,若q>0,此时方程(3)必存在一个正根;若q < 0,方程(3)不存在正根. 当R0 < 1时,
定义
则有等价关系
当满足R0 < 1且q>0时,有
1) R0=R0c⇔方程(3)有一个正根;
2) R0>R0c⇔方程(3)有两个正根;
3) R0<R0c⇔方程(3)没有正根.
此外当R0 < 1且q < 0,方程(3)不存在正根.
综上所述,有如下定理:
定理4 对于模型(1),有
1) 若R0>1,存在唯一的地方病平衡点;
2) 若R0≤1且q < 0,不存在地方病平衡点;
3) 若R0=1且q>0,存在唯一的地方病平衡点;
4) 若R0c < R0 < 1且q>0,存在两个地方病平衡点;
5) 若R0=R0c < 1且q>0,存在唯一的地方病平衡点;
6) 若R0<R0c < 1且q>0,不存在地方病平衡点.
-
本节将利用如下引理来计算分析后向分支存在的参数条件.
引理1[10] 考虑如下具有一般参数φ的常微分系统:
其中0是系统(4)的一个平衡点,满足f(0,φ)= 0. 假设:
(A1)
$\mathscr{A}=D_{x} f(\bf{0}, 0)=\left(\frac{\partial f_{i}}{\partial x_{j}}(\bf{0}, 0)\right)$ 是系统(4)在x= 0,φ=0时的线性化矩阵. 0是$\mathscr{A}$ 的单特征值,且$\mathscr{A}$ 的其他特征值具有负实部;(A2)
$\mathscr{A}$ 的0特征根有非负的右特征向量w和左特征向量v.设fk是f的第k个分量,定义:
则系统(4)在x=0处的局部动力学性质完全由a,b决定:
1) 若a>0,b>0. 当φ < 0,|φ|≪1时,x=0局部渐近稳定,且存在一个正的不稳定的平衡点;当0 < φ≪1时,x=0是不稳定的,且存在一个负的局部渐近稳定的平衡点;
2) 若a < 0,b < 0. 当φ < 0,|φ|≪1时,x=0是不稳定的;当0 < φ≪1时,x=0局部渐近稳定,且存在一个正的不稳定的平衡点;
3) 若a>0,b < 0. 当φ < 0,|φ|≪1时,x=0是不稳定的,且存在一个局部渐近稳定的负平衡点;当0 < φ≪1时,x=0是稳定的,且存在一个正的不稳定的平衡点;
4) 若a < 0,b>0. 当φ从负变为正时,x=0的稳定性从稳定变为不稳定,相应的一个负的不稳定的平衡点变为正的局部渐近稳定的平衡点.
由上述引理可以知道:当a>0,b>0时,系统会在φ=0处出现后向分支. 若a < 0,b>0,系统在φ=0有前向分支. 下面将运用引理1来找出模型(1)中前向分支、后向分支的存在条件,定义
定理5 若R*>1,模型(1)在R0=1处发生后向分支;若R* < 1,则模型(1)在R0=1处有前向分支.
证 选择β作为分支参数,当R0=1时,有
下面验证模型(1)在无病平衡点
$\boldsymbol{E}_{0}=\left(\frac{A}{\mu-B}, 0, 0, 0\right)$ 处满足引理1中的A1,A2条件. 根据引理1,记x=(S,I,H,R),有f在(E0,β*)处的线性化矩阵为
A的特征方程:
显然0是A的特征单根,且其他特征根都具有负实部. 引理1中的A1成立.
计算A的0特征根的右特征向量w,有
结果为
同理计算左特征向量v:
可得
引理中的A2满足.
下面计算参数a,b. 根据a,b的表达式和v可知,只需计算f2在(E0,β*)处的各项偏导数. 结果为
其余偏导数都为零. 由此可得:
显然,b>0是成立的. 接下来讨论a的情况,将β*的表达式代入a,可得
根据R*的定义,则有
由引理1可知,当R*>1时,模型(1)在R0=1处发生后向分支. 若R* < 1时,模型(1)在R0=1处出现前向分支.
3.1. 地方病平衡点的存在性
3.2. 后向分支
-
下面对理论结果进行简单的数值模拟.
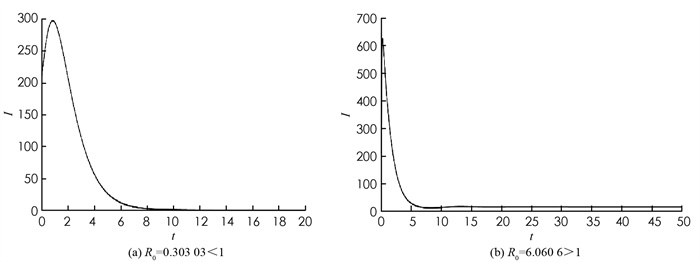
令A=10,B=0.001,β=0.003,μ=0.1,r=0.5,K=200,γ1=0.2,γ2=0.8,ε1=0.2,ε2=0.1. 此时,R0=0.303 03 < 1,其感染者(I)的数量随时间变化见图 1(a),可以看到无病平衡点局部渐近稳定.
令A=20,B=0.001,β=0.03,μ=0.1,r=0.5,K=200,γ1=0.2,ε1=0.2,γ2=0.8,ε2=0.1. 这时,R0=6.060 6>1. 在这种情况下,无病平衡点不稳定,存在一个地方病平衡点,疾病不能被消灭(图 1(b)).
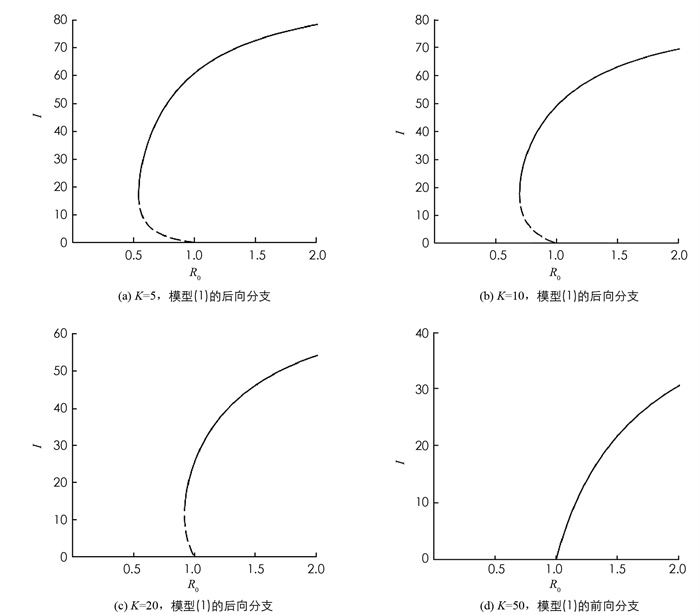
由R*的表达式可知,K越大,R*越小,模型(1)出现后向分支的可能性越低. 选取参数值:A=20,μ=0.008,r=0.5,B=0.001,γ1=0.1,γ2=0.3,ε1=0.1,ε2=0.05. K分别取5,10,20,50,对应的R*分别为:5.667 520 352,2.881 267 908,1.488 141 687,0.652 265 954 5,数值模拟得到图 2. 可以看到随着K的增大,R*在减小,模型(1)出现后向分支的区域越小. 当K增大到一定程度时,R* < 1,后向分支消失,出现前向分支,这与定理5的结论一致.
-
本文将人群分为易感者(S)、感染者(I)、住院者(H)、康复者(R). 考虑到非线性出生率和医院收治能力有限,本文建立了一类SIHR模型. 我们对模型的动力学性质进行了分析和讨论,得到了:R0 < 1时,无病平衡点局部渐近稳定. 同时定理4指出地方病平衡点的存在情况. 基于此,运用文献[10]中的定理,得到了后向分支的存在条件,即:当R*>1,模型会在R0=1处发生后向分支. 分析定理5中的R*,可知K与R*成反比,增大K会使得后向分支出现的可能性降低. 那么,增大医院容纳量,提高医疗条件,尽可能收治病人,有助于控制病情的传播. 另外,本文未对地方病平衡点的稳定性进行探讨,之后可以进一步讨论.



 下载:
下载: