本节讨论没有水流的影响，及q=0的情形下，系统(2)的Turing不稳定性.

假设(u_*，v_*)是系统(2)的常数稳态解，将系统(2)在(u_*，v_*)处线性化，令ϕ=u-u_*，φ=v-v_*，则有

其中f₁=f_u(u_*，v_*)，f₂=f_v(u_*，v_*)，g₁=g_u(u_*，v_*)，g₂=g_v(u_*，v_*). 用矩阵表示为

其中

在一维Neuman边界条件情形下，系统(4)解的形式为

其中$k=\frac{n \pi}{L}$，$n \in \mathbb{N}^{+}$. 要寻求系统(4)的非平凡解，则需

其中

如果系统(4)是一个线性不稳定的系统，那对于某些$n \in \mathbb{N}^{+}$，当t ∞时，Ψ(x，t)将会趋于无穷. 即在(5)式的解中某个ω存在正实部，或者矩阵M_k=-k²D + J的某个特征值有正实部，这取决于M_k的迹和行列式值的符号：

在(5)式中ω=ω(k)是决定稳态(u_*，v_*)稳定性的特征值. 对于k=0，(6)式的两个根满足

假设

这意味着稳态(u_*，v_*)在没有空间作用的情况下是线性稳定的. 现在对于k>0，(6)式的两个根满足

因为d₁>0，d₂>0并且假设(10)式成立，那对于所有$k=\frac{n \pi}{L}$，$n \in \mathbb{N}^{+}$都有ω₁^k+ω₂^k < 0. 因此，如果对于所有k>0都有ω₁^kω₂^k>0，那么(u_*，v_*)仍然保持稳定. 如果对于某些k>0有ω₁^kω₂^k < 0，那么(u_*，v_*)变得不稳定，这种由扩散导致的不稳定性通常被称作Turing不稳定，意味着模式的形成.

假设(10)式成立，当d₁g₂+d₂f₁>0时，Det(M_k)在k²=k_min²=$\frac{d_1 g_2+d_2 f_1}{2 d_1 d_2}$处取得最小值. 这时Det(M_k)>0等价于(d₁g₂+d₂f₁)²-4d₁d₂|J|>0. 那么系统(2)的空间齐次稳态解(u_*，v_*)可能失去稳态当且仅当

和

同时成立. 在(12)，(13)式同时成立的情况下，将Det(M_k)=0的两根设为k₁²，k₂²

当存在$n \in \mathbb{N}^{+}$，使得k²∈(k₁²，k₂²)，那空间齐次稳态(u_*，v_*)就会失去稳定，发生Turing不稳定，就有空间模式的形成. 故模式的形成只需不等式k₂-k₁>$\frac{\pi}{L}$成立即可.

经计算(k₂-k₁)²=$\frac{\left(d_1 g_2+d_2 f_1\right)-2 \sqrt{d_1 d_1 \mid \boldsymbol{J}\mid}}{d_1 d_2}$，则k₂-k₁>$\frac{\pi}{L}$等价于

事实上不等式(15)是不等式(13)的充分条件. 通过上面讨论得出如下定理.

定理1  假设(10)，(12)，(15)式同时成立的情况下，系统(2)的空间齐次稳态解(u_*，v_*)会发生Turing不稳定.

接下来考虑在发生Turing不稳定后，加入对流的情况，即系统(2)中q>0.

在一维的Neuman边界条件下，经计算可得dF_xx-qF_x=-λF的特征值分别为：λ₀=0，对应特征函数$F_0=C \mathrm{e}^{\frac{q}{d} x}$；λ_k=dk²+$\frac{q^2}{4 d}$，k=$\frac{n \pi}{L}$，$n \in \mathbb{N}^{+}$，对应特征函数F_k=C$\left[\mathrm{e}^{\frac{q}{2 d} x}\left(\frac{q}{2 k d} \sin k x+\cos k x\right)\right]$.

这时系统(4)解的形式变为

同上讨论，(6)式变成：

其中

M_k的迹和行列式值为：

已知ω₁^k+ω₂^k < 0.Det(M_k)=0可写成：

其中a=$\frac{1}{16 d_1 d_2}$，b=$\left(\frac{d_1 k^2}{4 d_2}+\frac{d_2 k^2}{4 d_1}-\frac{g_2}{4 d_1}-\frac{f_1}{4 d_2}\right)$，c=d₁d₂k⁴-(d₁g₂+d₂f₁)k²+|J|.

在q=0时，若系统(2)发生Turing不稳定则k²∈(k₁²，k₂²)，此时d₁d₂k⁴-k²(d₁g₂+d₂f₁)+|J| < 0. 由此可知当q>0时，只有一个正解q_*²=Q_*，

此时若$q < \sqrt{Q_*}$则ω₁^k+ω₂^k < 0，ω₁^kω₂^k < 0，空间齐次稳态解(u_*，v_*)仍然不稳定；若$q < \sqrt{Q_*}$ω₁^k+ ω₂^k < 0，ω₁^kω₂^k>0，空间齐次稳态解(u_*，v_*)重新稳定. 综上讨论，得出以下结论：

定理2  假设(10)，(12)，(15)式同时成立，系统(2)的空间齐次稳态解(u_*，v_*)会产生Turing不稳定. 加入对流项之后，当$q < \sqrt{Q_*}$时，空间齐次稳态解仍然不稳定；当$q>\sqrt{Q_*}$时，空间齐次稳态解会重新稳定.

标准的Lotka-Volterra捕食-食饵模型假设单位捕食率只依赖于食饵的数量. 但在大多数情况下，特别是当捕食者需要花更多时间去寻找食物时，更适合的捕食-食饵系统应建立在所谓的比例依赖性理论上^[12]. 也就是说，单位捕食者增长率应该是食饵与捕食者比值的函数. 文献[13-14]讨论了扩散驱动捕食-食饵模型产生空间结构的一些条件. 近年来一些研究者研究了比例依赖(即反应项具有收获率)的捕食-食饵模型^[15-16]. 我们考虑生活在河流生态系统中的捕食和食饵种群的相互作用，研究以下具有捕食者收获率的反应-扩散-对流比例依赖捕食-食饵模型的时空模型

其中：u(x，t)，u(v，t)分别代表食饵与捕食者的密度，r表示食饵的内在增长率，K代表环境容纳量，c代表捕获率，c₁代表转化系数，m代表半捕获饱和常数，e代表捕食者死亡率，h代表收获率. 为了方便，对系统(19)进行无量纲化：

仍记变量为u，v，x，t，q，则系统(19)可以写成

其中：$\alpha=\frac{c K}{m r}$，$\gamma=\frac{e}{r}$，$\beta=\frac{c_1 c}{r}$，$\delta=\frac{h}{r}$，$d=\frac{D_2}{D_1}$.

系统(20)对应的常微分系统为

计算可知模型(21)有唯一的正平衡点E_*=(u_*，v_*)=$\left(1-\alpha+\frac{\alpha(\gamma+\delta)}{\beta}, \left(\frac{\beta-\delta-\gamma}{\gamma+\delta}\right) u_*\right)$的充要条件是

(H₁) δ₁ < δ < β-γ，其中δ₁=max$\left\{0, \beta-\gamma-\frac{\beta}{\alpha}\right\}$.

模型(21)在E_*的Jacobian矩阵为

其中：

对应的特征多项式为

对于Jacobian矩阵J_(u*，v*)有如下结论.

引理1  1) 如果(H₁)成立，则f₁g₂-f₂g₁>0.

2) 如果

(H₂)αβ²+β(γ+δ)² < α(γ+δ)²+(γ+δ+1)β²成立，则f₁+g₂ < 0.

3) 如果

(H₃)αβ²+β(γ+δ)²>α(γ+δ)²+(γ+δ+1)β²成立，则f₁+g₂>0.

通过对Jacobian矩阵J的讨论，可得出如下结论.

定理3  假设(H₁)成立. 如果(H₂)成立，系统(21)的唯一正平衡点E_*是局部渐进稳定的；但如果(H₃)成立，系统(21)的唯一正平衡点E_*是不稳定的.

系统(21)正平衡点E_*也是系统(20)的空间齐次稳态解. 由定理1知，发生Turing不稳定当且仅当

在发生Turing不稳定后, 根据定理2知, 当$q>\sqrt{Q_*}$, 不稳定的E_* = (u_*, v_*) 空间齐次稳态解会重新稳定, 其中Q_*的表达式见定理2.

下面利用Matlab对上诉模型进行数值模拟，以此来验证以上理论分析的结果.

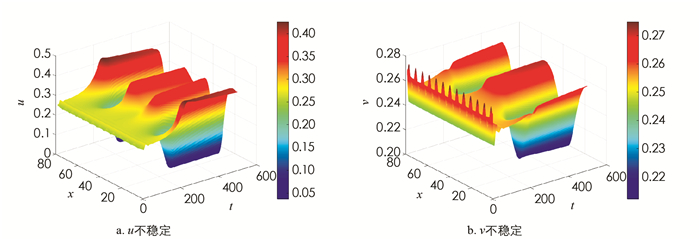
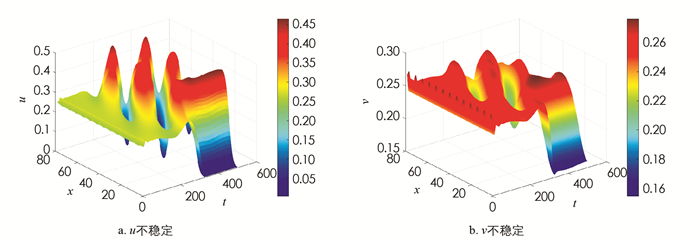
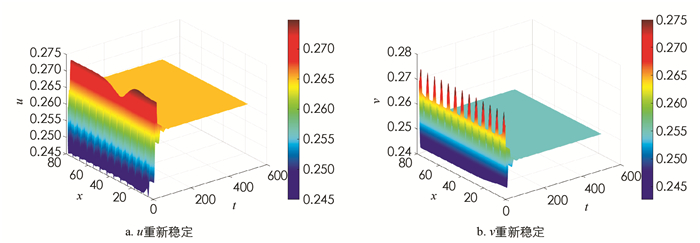
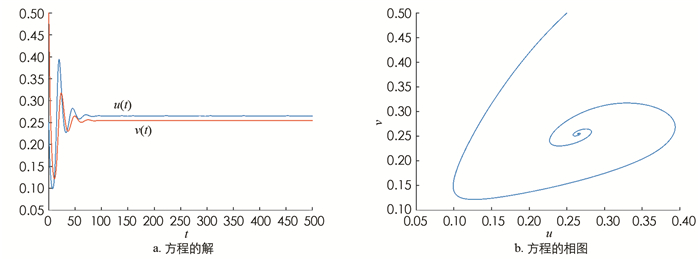
取参数为α=1.5，β=1.0，γ=0.01，δ=0.5. 此时正常数平衡点E_*=(0.265，0.255)是渐近稳定的(图 1). 现加入扩散，取d=50，L=25π，(u₀，v₀)=(0.265+0.01sin(x)，0.255+0.01sin(x))，(22)式的4个不等式均满足，此时发生Turing不稳定，有空间模式形成(图 2). 在发生不稳定后加入对流项. 在前面取定的参数情况下，计算得k₁²=0.121 2，k₂²=0.300 2，取n=4，则k²=0.16∈(k₁²，k₂²). 此时Q_*=0.360 6，取q=0.2，$q < \sqrt{Q_*}$，此时正常数平衡点仍然不稳定(图 3)；但取q=1.5，则$q>\sqrt{Q_*}$，正常数平衡点重新稳定(图 4).

我们利用反应―扩散―对流方程来描述河流生态系统中的捕食者与食饵的相互作用，研究了在河流长度一定的条件下发生Turing不稳定性的一些必要条件，还研究了对流项对Turing不稳定的影响. 发现存在一个对流系数临界值，当对流系数大于临界值时会使发生Turing不稳定的常数平衡解重新稳定，但当对流系数小于临界值时，加入对流项对Turing不稳定性不产生影响. 但本文研究的情况比较特殊，本文中的边界条件是一维Neuman边界条件，还假设了对流项系数相等. 如果对流项系数不等，那么河流长度无限长等情况都有待进一步研究.