-
众所周知,原油是工业生产的命脉,对国家的经济发展、贸易往来等多方面起着至关重要的作用. 原油期货(Crude Oil Future)是以远期石油价格为标的物的一类石油期货,自期货诞生以来,学者们就对其产品设计、定价方法、期现关系理论等展开了研究. 文献[1]提出双因素模型,该模型较好地预测了原油期货价格的趋势,其方程如下:
其中:dW1与dW2是标准布朗运动的增量,且dW1dW2=ρdt,μ是升值率,σ1与σ2是波动率,
$ \alpha=\mu-\frac{\sigma^2}{2 k} $ ,k是均值回复率. 文献[2]提出现货价格的双因子模型,该模型将对数现货价格分解成短期波动和长期均衡,短期波动X1t假定其服从期望为0的O-U过程,长期均衡X2t服从布朗运动. 其模型如下:其中k,μ,σ1,σ2为模型参数. 文献[3]根据期货价格的特征,建立仿射期限结构模型,该模型假定现货价格的自然对数可以分解成多个状态变量的和:
其中Xit(i=1,2,3,…,n)表示影响价格变化的因素.
原油期货的定价模型一般会假设随机变量服从连续随机过程,但是如遇战争等突发事件大概率会导致原油价格出现跃动,并且会影响很多相关产业[4-6]. 在此方面,很多学者也进行了分析研究,并得出相关的实用性模型[7-9].
文献[10]将跳跃扩散过程引入到石油期货价格的定价模型中,揭示了期货价格的变化特征. 文献[11]研究了天然气价格跳跃下的期货动态定价模型. 文献[12]则通过商品期货研究,建立了跳跃-扩散模型,其模型表示如下:
其中:Xt为标的资产的状态向量,JdNt(λ)是跳跃强度为λ的跳跃过程,J为跳跃强度.
依据受2020年疫情影响的我国原油期货价格特征,本文在文献[13]三因素原油期货定价模型的基础上考虑价格的跳跃性,并结合现货价格[14-15]的相关关系进行建模研究.
首先设现货价格取自然对数后可以分解如下:
其中:短期偏离X1t和中期偏离X2t均服从O-U过程,期望为0,而长期均衡X3t服从布朗运动. 其模型如下:
其中:k1,k2分别为短期偏离变量、中期偏离变量的均值回复率;μ为长期均衡变量的漂移率;σ1,σ2,σ3分别为X1t,X2t,X3t的波动率;dW1,dW2,dW3分别为X1t,X2t,X3t的标准布朗运动增量,且有
N1,N2和N3分别表示跳跃强度h1,h2和h3的泊松过程,J1,J2和J3分别为X1t,X2t和X3t的跳跃度大小,N1,N2和N3相互独立. 为了能够更好地推导出期货价格的解析解,选择跳跃度大小满足正态分布. 假设Ji(i=1,2,3)服从正态分布,即
另外,为了确保x1t和x2t的长期零均值,分别定义c1和c2为c1=h1γ1,c2=h2γ2.
为合理求得期货价格,加入风险溢价因子,建立本文研究的模型如下:
全文HTML
-
针对带有跳跃性因素的原油期货定价模型(1),对其进行求解,得到原油期货的定价公式. 求解步骤如下:
1) 求解X1t,X2t,X3t
对(1)式中的第一个等式同乘ek1t并且移项,且由微分d(uv)=udv+vdu得
两边积分得
移项同时除以ek1t,即得X1t的表达式为
同理由(1)式中的第二个等式求得X2t的表达式为
对(1)式中的第三个等式两边积分并移项即得X3t的表达式为
2) 求解lnSt的期望
为了求得期货价格,先求解lnSt的期望和方差. 按期望性质首先有
由
$ {\mathrm{d}} W_i(s)=\sqrt{\Delta s} U_i $ ,i=1,2,3,本文中Δs,Δt都表示时间增量,故有又EU1=0,所以
由泊松过程的定义知
即得
从而
由此得到X1t的期望,同理可得X2t和X3t的期望,它们分别为
进而可得lnSt的期望:
3) 求解lnSt的方差
按方差的性质有
首先求解X1t,X2t,X3t的方差:
同理求得
接下来求解Cov(X1t,X2t),Cov(X1t,X3t),Cov(X2t,X3t)
同理求得
进而可得lnSt的方差:
4) 模型的解析解
由对数正态分布的特性lnE[St]=E[lnSt]+
$ \frac{1}{2} D\left[\ln S_t\right] $ 可知,若给定状态变量初始值,根据F(0,t)=E[St]得到初始时刻的期货价格解析解:所以t时刻的期货价格解析解:
其中T为期货到期期限,(2)式即为考虑跳跃性因素的原油期货定价模型的解析解.
-
若一天内只发生一次跳跃,则泊松过程就是伯努利过程,将(1)式离散化并移项得
同理求得
其中:Ui(i=1,2,3) 为标准正态随机变量,Bi(i=1,2,3)为独立的伯努利随机变量,且有
本文给出如下记号:
其中wt1=x1t-(1-k1Δt)x1t-Δt+λ1Δt=
$ \sigma_1 \sqrt{\Delta t} U_1+J_1 B_1 $ .我们选取n个Δx1t=x1t-x1t-Δt数据,由于Δx1t服从正态分布,剔除异常数据后计算出均值
$ \overline{\Delta x_{1 t}} $ ,方差s. 本文由($ \overline{\Delta x_{1 t}} $ -3s,$ \overline{\Delta x_{1 t}} $ +3s)之外的数据获得m1个跳跃数据.n-m1个正常数据的密度函数为
样本的似然函数为
需要估计的参数有Θ1={k1,λ1,σ1},对数似然函数为:
进而似然方程为:
即得方程组
解得
m1个跳跃数据wt1的密度函数为
样本的似然函数为
需要估计的参数Θ2={γ1,δ1},对数似然函数为
进而得似然方程为
解得
同理得
至此,考虑跳跃性因素的原油期货定价模型中的所有参数有了详细的估计公式. 利用此定价公式和参数估计方法,可以依据疫情环境下具体原油期货合约的数据,对跳跃性因素下的原油期货进行分析和定价.
-
采用平均绝对误差(MAE)和均方根误差(RMSE)统计量,评价模型的拟合和预测能力[14],公式如下:
其中:
$\tilde{F}(t, T)$ 为预测值;F(t,T)为真实值. -
选取上海期货交易所的4种短期主力合约(期限均为1年),选取4种长期合约(期限均为3年). 将4种长期期货合约价格的对数均值作为长期均衡变量的观测值;将所有长期合约价格的均值对数值减去所有短期合约价格的均值对数值的结果作为短期偏离的观测值;将现货价格的对数值减去短期偏离值和长期均衡值之和所得的差值做为中期偏离的数值;原油现货价格从Choice金融终端软件取得. 选取上海期货交易所的4种短期主力合约(期限均为1年),短期期货合约代码分别为sc1907,sc1908,sc1909,sc1910;选取4种长期合约(期限均为3年),长期合约代码分别为sc2103,sc2106,sc2109,sc2112. 将2019年1月至6月的期货合约数据按上述方法处理后得到短期偏离、中期偏离、长期均衡值. 在数据日期选择方面,由于上海期货交易中心在法定节假日没有期货合约交易数据,所以本文剔除了大庆原油现货价格法定节假日的数据,以便与上海原油期货价格数据保持一致. 由三因素原油期货定价模型的参数估计表达式,利用excel表格进行模型参数的计算,得到三因素原油期货定价模型的参数如表 1所示.
我们选取上海期货交易所的4种短期主力合约(期限均为1年),短期期货合约代码分别为sc2007,sc2008,sc2009,sc2010;选取4种长期合约(期限均为3年),长期期货合约代码分别为sc2203,sc2206,sc2209,sc2212. 短期偏移变量、中期偏移变量、长期均衡变量的取值均按照上述方法获得. 对2020年1月至6月的期货合约数据进行参数的估计,同样剔除了大庆原油现货价格法定节假日的数据. 由模型的参数估计方法,在n=116个数据中经过计算得到3类跳跃数据,其数据量分别为m1=43,m2=67,m3=36,计算出h3=0.310 3. 利用excel表格进行参数的计算,得到带有跳跃性因素的原油期货定价模型的参数如表 2所示.
-
利用三因素原油期货定价模型对sc1911原油期货进行预测,预测期限为2019年8月. 依据三因素原油期货定价模型的解析解公式得出预测值,依据上海期货交易所的每日结算价得到原油期货合约的真实值. 对两种数据的比较结果见表 3.
利用三因素原油期货定价模型对sc2108原油期货合约进行预测,预测期限为2020年8月. 依据三因素原油期货定价模型的解析解公式得出预测值,通过上海期货交易所的每日结算价得到原油期货合约的真实值,如表 4所示.
为了更精确得到模型的拟合和预测能力,本文给出了模型的拟合能力评价标准,利用公式(3)和公式(4)对三因素模型得到的预测值与真实值进行计算,得到三因素原油期货模型拟合能力评价值如表 5所示.
由于模型拟合能力评价值越小说明模型的预测能力越好,从表 5中得出三因素模型对2019年的原油期货合约预测能力较好,对于2020年该模型的预测能力较差.
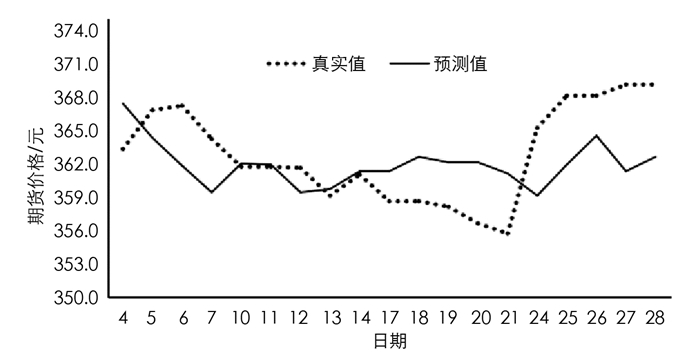
利用带有跳跃性因素原油期货定价模型对sc2108原油期货进行预测,预测期限为2020年8月. 依据考虑跳跃性因素的原油期货定价模型解析解公式(2)得出预测值,通过上海期货交易所的每日结算价得到sc2108原油期货合约的真实值,如表 6所示.
依据预测值和真实值数据绘制出对比图(图 1).
进一步给出模型的拟合能力评价标准. 利用公式(3)和公式(4)对考虑跳跃性因素的原油期货定价模型得到的预测值与真实值进行拟合能力评价,其中:FMAE=-0.535,FRMSE=3.7637.
经与表 5中得出的拟合能力评价值比较,三因素模型对2019年的原油期货合约预测能力较好,对于2020年该模型的预测能力较差. 考虑跳跃性因素的原油期货模型对受疫情影响的2020年的原油期货价格的预测能力较好,说明该模型具有一定的科学性和实用性,可为从事原油期货的研究及实务人员从事相关研究和实务操作提供一定的理论依据和参考信息.



 下载:
下载: