高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

面向不完备单值中智信息的三支决策模型

, 

上一篇

下一篇

杨海龙, 任欢欢. 面向不完备单值中智信息的三支决策模型[J]. 西南师范大学学报(自然科学版), 2023, 48(7): 1-10. doi: 10.13718/j.cnki.xsxb.2023.07.001
引用本文: 杨海龙, 任欢欢. 面向不完备单值中智信息的三支决策模型[J]. 西南师范大学学报(自然科学版), 2023, 48(7): 1-10. doi: 10.13718/j.cnki.xsxb.2023.07.001
shu
YANG Hailong, REN Huanhuan. Three-Way Decision Model Facing Incomplete Single-Valued Neutrosophic Information[J]. Journal of Southwest China Normal University(Natural Science Edition), 2023, 48(7): 1-10. doi: 10.13718/j.cnki.xsxb.2023.07.001
Citation: YANG Hailong, REN Huanhuan. Three-Way Decision Model Facing Incomplete Single-Valued Neutrosophic Information[J]. Journal of Southwest China Normal University(Natural Science Edition), 2023, 48(7): 1-10. doi: 10.13718/j.cnki.xsxb.2023.07.001
shu

面向不完备单值中智信息的三支决策模型

  • 陕西师范大学 数学与统计学院，西安 710119

  • 基金项目: 国家自然科学基金项目(12171293)
详细信息
    作者简介:

    杨海龙，教授，博导，主要从事智能信息处理、三支决策与粗糙集的研究 .

  • 中图分类号: O225;TP18

Three-Way Decision Model Facing Incomplete Single-Valued Neutrosophic Information

  • School of Mathematics and Statistics, Shaanxi Normal University, Xi'an 710119, China

  • 摘要:

    首先，给出了单值中智信息系统和不完备单值中智信息系统的概念，在此基础上，利用平均值法将一个不完备单值中智信息系统补全为完备的单值中智信息系统；然后，基于补全的单值中智信息系统给出了对象间的相似度的定义，进一步建立了面向不完备单值中智信息的三支决策模型；最后，通过例子阐述了模型的具体应用，并讨论了模型中的参数对决策结果的影响.

    Abstract:

    Firstly, the concepts of single-valued neutrosophic information systems and incomplete single-valued neutrosophic information systems are given. On the basis of these conceptions, an incomplete single-valued neutrosophic information system is converted into a complete single-valued neutrosophic information system by supplementing the missing values with mean value method. Then similarity degrees between objects are defined based on the supplemented single-valued neutrosophic information system. Furthermore, a three-way decision model facing incomplete single-valued neutrosophic information is constructed. Finally, the application of proposed model is illustrated by an example. Besides, the influence of the parameters in the model on the decision results is discussed.

  • 加载中

  • 图 1  当α变化时的决策结果

    下载: 全尺寸图片 幻灯片

    表 1  损失函数

    C ¬C
    πP(接受) γPP γPN
    πB(不承诺) γBP γBN
    πN(拒绝) γNP γNN
    下载: 导出CSV

    表 2  不完备单值中智信息系统

    a1 a2 a3
    u1 (0.6，0.4，0.3) (*，*，*) (0.3，0.4，0.8)
    u2 (0.4，0.1，*) (0.9，0.2，0.3) (0.5，0.6，0.7)
    u3 (0.5，0.5，0.3) (*，0.1，0.4) (0.7，*，0.9)
    u4 (0.2，0.7，0.6) (0.5，0.4，0.6) (*，*，0.3)
    下载: 导出CSV

    表 3  由平均值法诱导的完备单值中智信息系统

    a1 a2 a3
    u1 (0.6，0.4，0.3) (0.7，0.4，0.7) (0.3，0.4，0.8)
    u2 (0.4，0.1，0.4) (0.9，0.2，0.3) (0.5，0.6，0.7)
    u3 (0.5，0.5，0.3) (0.7，0.1，0.4) (0.7，0.5，0.9)
    u4 (0.2，0.7，0.6) (0.5，0.4，0.6) (0.5，0.5，0.3)
    下载: 导出CSV
    算法1  基于不完备单值中智信息系统的三支决策的算法
    输入：不完备单值中智信息系统、损失函数和参数α(0 < α < 1)
    输出：每个对象u∈U的三支决策结果
    1)将不完备单值中智信息系统中的未知值用该属性下其他对象对应的属性值的平均值补全，得到补全的完备单值中智信息系统.
    2)对每个属性a∈A，计算对象间的相似度Sa(u，v).
    3)由公式(1)，计算对象间关于属性集A的相似度Sim(u，v).
    4)计算[u]SRα和P(C|[u]SRα).
    5)计算期望损失E(π·|[u]SRα)(·=P，B，N).
    6)基于期望损失计算得分函数sc(E(π·|[u]SRα))和精确度函数ac(E(π·|[u]SRα)).
    7)由(P*)-(N*)得到每个对象的三支决策结果.
    下载: 导出CSV

    表 4  关于供应商的不完备单值中智信息系统

    a1 a2 a3 a4 d
    u1 (0.37，0.25，0.41) (0.31，0.47，0.38) (*，*，*) (0.55，0.72，0.95) 0
    u2 (0.82，*，0.11) (0.29，0.21，0.63) (0.43，0.56，0.72) (0.09，*，0.10) 0
    u3 (0.79，0.80，0.45) (0.72，0.43，0.55) (0.22，0.59，0.31) (0.45，0.47，0.54) 1
    u4 (*，*，0.33) (0.93，0.47，0.63) (*，0.56，0.72) (0.38，0.23，0.66) 1
    u5 (0.23，0.87，0.92) (0.55，0.82，0.37) (0.79，0.73，0.23) (0.52，0.42，0.36) 0
    u6 (0.45，0.03，0.72) (0.49，0.50，*) (0.95，0.31，0.40) (0.65，0.39，0.10) 1
    u7 (0.57，0.42，0.69) (0.54，0.21，0.94) (0.52，0.21，0.46) (*，0.49，*) 0
    u8 (0.79，0.20，0.41) (0.74，0.31，0.29) (0.82，0.59，*) (0.09，0.38，0.10) 0
    u9 (0.33，0.70，0.56) (0.66，*，*) (0.27，0.36，0.74) (0.82，0.37，0.44) 1
    u10 (0.42*，0.33) (0.91，0.52，0.55) (0.53，0.71，0.23) (0.69，0.88，0.65) 0
    下载: 导出CSV

    表 5  损失函数

    γPP γBP γNP γPN γBN γNN
    u1 (0.21，0.55，0.62) (0.30，0.62，0.58) (0.51，0.28，0.77) (0.97，0.52，0.31) (0.46，0.50，0.07) (0.53，0.35，0.47)
    u2 (0.39，0.35，0.54) (0.50，0.17，0.45) (0.73，0.43，0.38) (0.88，0.61，0.15) (0.84，0.32，0.28) (0.36，0.52，0.62)
    u3 (0.14，0.25，0.87) (0.24，0.72，0.55) (0.85，0.04，0.29) (0.47，0.32，0.68) (0.55，0.49，0.90) (0.24，0.62，0.59)
    u4 (0.53，0.47，0.57) (0.80，0.62，0.84) (0.65，0.71，0.54) (0.71，0.54，0.63) (0.57，0.35，0.60) (0.44，0.17，0.65)
    u5 (0.11，0.44，0.56) (0.37，0.29，0.64) (0.73，0.53，0.17) (0.62，0.58，0.33) (0.47，0.29，0.28) (0.46，0.53，0.91)
    u6 (0.26，0.35，0.93) (0.56，0.47，0.56) (0.81，0.38，0.56) (0.54，0.69，0.37) (0.28，0.37，0.25) (0.14，0.16，0.45)
    u7 (0.42，0.70，0.87) (0.45，0.13，0.28) (0.64，0.88，0.43) (0.90，0.32，0.54) (0.46，0.82，0.84) (0.29，0.55，0.73)
    u8 (0.54，0.14，0.37) (0.64，0.56，0.33) (0.93，0.27，0.35) (0.85，0.73，0.22) (0.67，0.13，0.47) (0.25，0.77，0.64)
    u9 (0.34，0.71，0.49) (0.52，0.25，0.38) (0.77，0.36，0.54) (0.55，0.58，0.27) (0.62，0.25，0.61) (0.46，0.38，0.49)
    u10 (0.38，0.75，0.82) (0.39，0.48，0.75) (0.52，0.61，0.22) (0.80，0.52，0.40) (0.67，0.55，0.44) (0.33，0.23，0.71)
    下载: 导出CSV

    表 6  关于供应商的由平均值法诱导的完备单值中智信息系统

    a1 a2 a3 a4 d
    u1 (0.37，0.25，0.41) (0.31，0.47，0.38) (0.57，0.51，0.48) (0.55，0.72，0.95) 0
    u2 (0.82，0.47，0.11) (0.29，0.21，0.63) (0.43，0.56，0.72) (0.09，0.39，0.10) 0
    u3 (0.79，0.80，0.45) (0.72，0.43，0.55) (0.22，0.59，0.31) (0.45，0.47，0.54) 1
    u4 (0.53，0.47，0.33) (0.93，0.47，0.63) (0.57，0.56，0.72) (0.38，0.23，0.66) 1
    u5 (0.23，0.87，0.92) (0.55，0.82，0.37) (0.79，0.73，0.23) (0.52，0.42，0.36) 0
    u6 (0.45，0.03，0.72) (0.49，0.50，0.54) (0.95，0.31，0.40) (0.65，0.39，0.10) 1
    u7 (0.57，0.42，0.69) (0.54，0.21，0.94) (0.52，0.21，0.46) (0.47，0.49，0.43) 0
    u8 (0.79，0.20，0.41) (0.74，0.31，0.29) (0.82，0.59，0.48) (0.09，0.38，0.10) 0
    u9 (0.33，0.70，0.56) (0.66，0.44，0.54) (0.27，0.36，0.74) (0.82，0.37，0.44) 1
    u10 (0.42，0.47，0.33) (0.91，0.52，0.55) (0.53，0.71，0.23) (0.69，0.88，0.65) 0
    下载: 导出CSV

    表 7  关于属性a1的相似度Sa1(u，v)

    Sa1(u，v) u1 u2 u3 u4 u5 u6 u7 u8 u9 u10
    u1 1.000 0 0.312 5 0.385 0 0.385 0 0.337 5 0.402 5 0.380 0 0.395 0 0.452 5 0.467 5
    u2 0.312 5 1.000 0 0.407 5 0.372 5 0.150 0 0.255 0 0.292 5 0.417 5 0.265 0 0.345 0
    u3 0.385 0 0.407 5 1.000 0 0.405 0 0.242 5 0.347 5 0.385 0 0.490 0 0.357 5 0.377 5
    u4 0.385 0 0.372 5 0.405 0 1.000 0 0.277 5 0.382 5 0.400 0 0.415 0 0.392 5 0.472 5
    u5 0.337 5 0.150 0 0.242 5 0.277 5 1.000 0 0.395 0 0.357 5 0.232 5 0.385 0 0.305 0
    u6 0.402 5 0.255 0 0.347 5 0.382 5 0.277 5 1.000 0 0.462 5 0.337 5 0.430 0 0.395 0
    u7 0.380 0 0.292 5 0.385 0 0.400 0 0.395 0 0.462 5 1.000 0 0.375 0 0.407 5 0.372 5
    u8 0.395 0 0.417 5 0.490 0 0.415 0 0.232 5 0.337 5 0.375 0 1.000 0 0.347 5 0.387 5
    u9 0.452 5 0.265 0 0.357 5 0.392 5 0.385 0 0.430 0 0.407 5 0.347 5 1.000 0 0.420 0
    u10 0.467 5 0.345 0 0.377 5 0.472 5 0.305 0 0.395 0 0.372 5 0.387 5 0.420 0 1.000 0
    下载: 导出CSV

    表 8  对象间的相似度

    Sim(u，v) u1 u2 u3 u4 u5 u6 u7 u8 u9 u10
    u1 1.000 0 0.330 6 0.370 6 0.373 1 0.375 6 0.366 3 0.378 8 0.337 5 0.372 5 0.398 1
    u2 0.330 6 1.000 0 0.356 3 0.366 3 0.283 8 0.333 1 0.348 8 0.514 4 0.334 4 0.308 8
    u3 0.370 6 0.356 3 1.000 0 0.398 8 0.357 5 0.355 6 0.399 4 0.381 9 0.400 6 0.411 3
    u4 0.373 1 0.366 3 0.398 8 1.000 0 0.332 5 0.341 9 0.391 9 0.361 9 0.389 4 0.433 8
    u5 0.375 6 0.283 8 0.357 5 0.332 5 1.000 0 0.414 4 0.389 4 0.355 6 0.365 6 0.372 5
    u6 0.366 3 0.333 1 0.355 6 0.341 9 0.414 4 1.000 0 0.400 0 0.380 0 0.376 3 0.373 1
    u7 0.378 8 0.348 8 0.399 4 0.391 9 0.389 4 0.400 0 1.000 0 0.351 3 0.388 8 0.378 1
    u8 0.337 5 0.514 4 0.381 9 0.361 9 0.355 6 0.380 0 0.351 3 1.000 0 0.323 8 0.339 4
    u9 0.372 5 0.334 4 0.400 6 0.389 4 0.365 6 0.376 3 0.388 8 0.323 8 1.000 0 0.394 4
    u10 0.398 1 0.308 8 0.411 3 0.433 8 0.372 5 0.373 1 0.378 1 0.339 4 0.394 4 1.000 0
    下载: 导出CSV

    表 9  期望损失

    E(πP|[u]SR0.37) E(πB|[u]SR0.37) E(πN|[u]SR0.37)
    u1 (0.878 1，0.532 7，0.417 2) (0.396 5，0.548 3，0.173 2) (0.521 5，0.318 1，0.580 7)
    u2 (0.880 0，0.610 0，0.150 0) (0.840 0，0.320 0，0.280 0) (0.360 0，0.520 0，0.620 0)
    u3 (0.347 8，0.287 9，0.755 7) (0.436 7，0.577 9，0.728 8) (0.620 9，0.191 5，0.435 2)
    u4 (0.630 8，0.503 8，0.599 2) (0.706 7，0.465 8，0.709 9) (0.557 3，0.347 4，0.592 5)
    u5 (0.549 5，0.548 8，0.366 8) (0.451 4，0.290 0，0.330 3) (0.529 9，0.530 0，0.650 6)
    u6 (0.461 0，0.550 3，0.503 1) (0.389 0，0.400 7，0.327 1) (0.480 1，0.213 5，0.484 0)
    u7 (0.759 2，0.473 3，0.685 4) (0.455 0，0.326 5，0.485 0) (0.494 4，0.695 7，0.560 3)
    u8 (0.737 3，0.319 7，0.285 3) (0.655 3，0.269 8，0.393 8) (0.770 9，0.456 0，0.473 3)
    u9 (0.439 9，0.651 1，0.379 5) (0.565 7，0.250 0，0.465 5) (0.668 4，0.368 4，0.518 0)
    u10 (0.647 9，0.624 5，0.572 7) (0.551 3，0.513 8，0.574 5) (0.432 9，0.374 6，0.395 2)
    下载: 导出CSV

    表 10  当α=0.37时期望损失的得分函数和精确度函数

    sc(E(πP|[u]SR0.37)) sc(E(πB|[u]SR0.37)) sc(E(πN|[u]SR0.37)) ac(E(πP|[u]SR0.37)) ac(E(πB|[u]SR0.37)) ac(E(πN|[u]SR0.37))
    u1 0.730 4 0.611 6 0.470 4 0.601 1 0.324 1 0.554 4
    u2 0.865 0 0.780 0 0.370 0 0.508 7 0.538 5 0.486 5
    u3 0.296 0 0.354 0 0.592 9 0.587 4 0.616 8 0.523 6
    u4 0.515 8 0.498 4 0.482 4 0.611 5 0.709 0 0.577 6
    u5 0.591 3 0.560 5 0.439 6 0.464 6 0.402 6 0.602 6
    u6 0.479 0 0.530 9 0.498 0 0.481 3 0.366 3 0.482 0
    u7 0.536 9 0.485 0 0.467 1 0.707 0 0.469 1 0.529 3
    u8 0.726 0 0.630 7 0.648 8 0.507 8 0.519 5 0.594 1
    u9 0.530 2 0.550 1 0.575 2 0.414 9 0.514 2 0.581 0
    u10 0.537 6 0.488 4 0.518 8 0.602 6 0.564 4 0.417 2
    下载: 导出CSV

    表 11  当α=0.36时期望损失的得分函数和精确度函数

    sc(E(πP|[u]SR0.36)) sc(E(πB|[u]SR0.36)) sc(E(πN|[u]SR0.36)) ac(E(πP|[u]SR0.36)) ac(E(πB|[u]SR0.36)) ac(E(πN|[u]SR0.36))
    u1 0.703 8 0.591 8 0.459 3 0.601 0 0.325 4 0.566 2
    u2 0.865 0 0.780 0 0.370 0 0.508 7 0.538 5 0.486 5
    u3 0.296 0 0.354 0 0.592 9 0.587 4 0.616 8 0.523 6
    u4 0.522 8 0.498 3 0.462 1 0.624 0 0.679 6 0.574 0
    u5 0.550 9 0.534 9 0.525 6 0.449 6 0.410 0 0.543 6
    u6 0.495 8 0.529 9 0.481 2 0.477 1 0.353 4 0.458 6
    u7 0.536 9 0.485 0 0.467 1 0.707 0 0.469 1 0.529 3
    u8 0.702 8 0.636 1 0.686 8 0.502 4 0.512 8 0.596 4
    u9 0.545 6 0.545 7 0.566 6 0.417 0 0.524 9 0.571 5
    u10 0.537 6 0.488 4 0.518 8 0.602 6 0.564 4 0.417 2
    下载: 导出CSV

    表 12  当α=0.365时期望损失的得分函数和精确度函数

    sc(E(πP|[u]SR0.365)) sc(E(πB|[u]SR0.365)) sc(E(πN|[u]SR0.365)) ac(E(πP|[u]SR0.365)) ac(E(πB|[u]SR0.365)) ac(E(πN|[u]SR0.365))
    u1 0.703 8 0.591 8 0.459 3 0.601 0 0.325 4 0.566 2
    u2 0.781 9 0.719 1 0.496 7 0.507 5 0.532 7 0.523 5
    u3 0.296 0 0.354 0 0.592 9 0.587 4 0.616 8 0.523 6
    u4 0.519 9 0.498 6 0.470 9 0.618 7 0.692 2 0.575 7
    u5 0.550 9 0.534 9 0.525 6 0.449 6 0.410 0 0.543 6
    u6 0.495 8 0.529 9 0.481 2 0.477 1 0.353 4 0.458 6
    u7 0.536 9 0.485 0 0.467 1 0.707 0 0.469 1 0.529 3
    u8 0.726 0 0.630 7 0.648 8 0.507 8 0.519 5 0.594 1
    u9 0.545 6 0.545 7 0.566 6 0.417 0 0.524 9 0.571 5
    u10 0.537 6 0.488 4 0.518 8 0.602 6 0.564 4 0.417 2
    下载: 导出CSV

    表 13  当α=0.375时期望损失的得分函数和精确度函数

    sc(E(πP|[u]SR0.375)) sc(E(πB|[u]SR0.375)) sc(E(πN|[u]SR0.375)) ac(E(πP|[u]SR0.375)) ac(E(πB|[u]SR0.375)) ac(E(πN|[u]SR0.375))
    u1 0.830 0 0.695 0 0.530 0 0.584 3 0.330 9 0.500 0
    u2 0.865 0 0.780 0 0.370 0 0.508 7 0.538 5 0.486 5
    u3 0.277 9 0.355 8 0.624 4 0.584 6 0.583 4 0.530 4
    u4 0.509 6 0.497 1 0.498 0 0.601 0 0.732 7 0.579 9
    u5 0.576 6 0.551 2 0.473 8 0.459 5 0.405 1 0.576 1
    u6 0.454 3 0.531 8 0.519 4 0.488 2 0.384 3 0.510 1
    u7 0.536 9 0.485 0 0.467 1 0.707 0 0.469 1 0.529 3
    u8 0.726 0 0.630 7 0.648 8 0.507 8 0.519 5 0.594 1
    u9 0.530 2 0.550 1 0.575 2 0.414 9 0.514 2 0.581 0
    u10 0.537 6 0.488 4 0.518 8 0.602 6 0.564 4 0.417 2
    下载: 导出CSV

    表 14  当α=0.38时期望损失的得分函数和精确度函数

    sc(E(πP|[u]SR0.38)) sc(E(πB|[u]SR0.38)) sc(E(πN|[u]SR0.38)) ac(E(πP|[u]SR0.38)) ac(E(πB|[u]SR0.38)) ac(E(πN|[u]SR0.38))
    u1 0.830 0 0.695 0 0.530 0 0.584 3 0.330 9 0.500 0
    u2 0.865 0 0.780 0 0.370 0 0.508 7 0.538 5 0.486 5
    u3 0.277 9 0.355 8 0.624 4 0.584 6 0.583 4 0.530 4
    u4 0.509 6 0.497 1 0.498 0 0.601 0 0.732 7 0.579 9
    u5 0.550 9 0.534 9 0.525 6 0.449 6 0.410 0 0.543 6
    u6 0.479 0 0.530 9 0.498 0 0.481 3 0.366 3 0.482 0
    u7 0.467 5 0.524 8 0.517 8 0.724 2 0.432 0 0.529 7
    u8 0.760 2 0.621 3 0.568 2 0.514 4 0.531 4 0.580 6
    u9 0.523 8 0.551 8 0.578 5 0.414 0 0.510 0 0.584 6
    u10 0.495 2 0.458 5 0.550 0 0.611 6 0.570 2 0.410 5
    下载: 导出CSV
  • [1] YAO Y Y. Three-Way Decisions with Probabilistic Rough Sets [J]. Information Sciences, 2010, 180(3): 341-353. doi: 10.1016/j.ins.2009.09.021
    [2] YAO Y Y. An Outline of a Theory of Three-Way Decisions [M]//Rough Sets and Current Trends in Computing. Heidelberg: Springer, 2012: 1-17.
    [3] YAO Y Y. The Superiority of Three-Way Decisions in Probabilistic Rough Set Models [J]. Information Sciences, 2011, 181(6): 1080-1096. doi: 10.1016/j.ins.2010.11.019
    [4] WANG H B, SMARANDACHE F, SUNDERRAMAN R. Single Valued Neutrosophic Sets [J]. Multispace Multistruct, 20104: 410-413.
    [5] ATANASSOV K T. Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96. doi: 10.1016/S0165-0114(86)80034-3
    [6] JIAO L, YANG H L, LI S G. Three-Way Decision Based on Decision-Theoretic Rough Sets with Single-Valued Neutrosophic Information [J]. International Journal of Machine Learning and Cybernetics, 2020, 11(3): 657-665. doi: 10.1007/s13042-019-01023-3
    [7] CHUTIA R, GOGOI M K, FIROZJA M A, et al. Ordering Single-Valued Neutrosophic Numbers Based on Flexibility Parameters and Its Reasonable Properties [J]. International Journal of Intelligent Systems, 2021, 36(4): 1831-1850. doi: 10.1002/int.22362
    [8] QIN K Y, WANG L. New Similarity and Entropy Measures of Single-Valued Neutrosophic Sets with Applications in Multi-Attribute Decision Making [J]. Soft Computing-A Fusion of Foundations, Methodologies and Applications, 2020, 24(21): 16165-16176.
    [9] ZHANG X H, BO C X, SMARANDACHE F, et al. New Inclusion Relation of Neutrosophic Sets with Applications and Related Lattice Structure [J]. International Journal of Machine Learning and Cybernetics, 2018, 9(10): 1753-1763. doi: 10.1007/s13042-018-0817-6
    [10] PENG J J. An Outranking Approach for Multi-Criteria Decision-Making Problems with Simplified Neutrosophic Sets [J]. Applied Soft Computing, 2014, 25: 336-346. doi: 10.1016/j.asoc.2014.08.070
    [11] 杨海龙, 任欢欢, 焦丽. 单值中智信息下的一种新型三支决策模型[J]. 陕西师范大学学报(自然科学版), 2022, 50(3)1-6. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SXSZ202203001.htm
    [12] GRZYMAŁA-BUSSE J W. Characteristic Relations for Incomplete Data: A Generalization of the Indiscernibility Relation [M]//Rough Sets and Current Trends in Computing. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004: 244-253.
    [13] LIU D, LIANG D, WANG C. A Novel Three-Way Decision Model Based on Incomplete Information System [J]. Knowledge-Based Systems, 2016, 91: 32-45. doi: 10.1016/j.knosys.2015.07.036
    [14] XUE Z A, XIN X W, YUAN Y L, et al. Intuitionistic Fuzzy Possibility Measure-Based Three-Way Decisions for Incomplete Data [J]. Journal of Intelligent & Fuzzy Systems, 2018, 35(5): 5657-5666.
    [15] LUO C, LI T, HUANG Y, et al. Updating Three-Way Decisions in Incomplete Multi-Scale Information Systems [J]. Information Sciences, 2019, 476: 274-289. doi: 10.1016/j.ins.2018.10.012
    [16] ZHAN J M, YE J, DING W P, et al. A Novel Three-Way Decision Model Based on Utility Theory in Incomplete Fuzzy Decision Systems [J]. IEEE Transactions on Fuzzy Systems, 2022, 30(7): 2210-2226. doi: 10.1109/TFUZZ.2021.3078012
    [17] WEN H L, XIA F, TANG H X. Three-Way Decision for Incomplete Real-Valued Data [J]. Journal of Intelligent & Fuzzy Systems: Applications in Engineering and Technology, 2020, 39(5): 7843-7862.
    [18] LUO J F, FUJITA H, YAO Y Y, etal. On Modeling Similarity and Three-Way Decision under Incomplete Information in Rough Set Theory [J]. Knowledge-Based Systems, 2020, 191: 1-14.
    [19] LUO J F, HU M J, QIN K Y. Three-Way Decision with Incomplete Information Based on Similarity and Satisfiability [J]. International Journal of Approximate Reasoning, 2020, 120: 151-183. doi: 10.1016/j.ijar.2020.02.005
  • 加载中
图( 1) 表( 15)
计量
  • 文章访问数:  412
  • HTML全文浏览数:  412
  • PDF下载数:  201
  • 施引文献:  0
出版历程
  • 收稿日期:  2022-06-07
  • 刊出日期:  2023-07-20

面向不完备单值中智信息的三支决策模型

    作者简介: 杨海龙，教授，博导，主要从事智能信息处理、三支决策与粗糙集的研究
  • 陕西师范大学 数学与统计学院，西安 710119
  • 收稿日期:  2022-06-07
基金项目:  国家自然科学基金项目(12171293)

摘要: 

首先，给出了单值中智信息系统和不完备单值中智信息系统的概念，在此基础上，利用平均值法将一个不完备单值中智信息系统补全为完备的单值中智信息系统；然后，基于补全的单值中智信息系统给出了对象间的相似度的定义，进一步建立了面向不完备单值中智信息的三支决策模型；最后，通过例子阐述了模型的具体应用，并讨论了模型中的参数对决策结果的影响.

English Abstract

    全文HTML

  • 三支决策[1-3]是处理决策问题的一个有效方法，其核心思想是将一个论域划分为三个两两不相交的部分，对每个部分制定相应的策略，以及对三分和策略进行评价. 三支决策的模型和理论已经被广泛研究并应用到了众多领域.

    单值中智集[4]作为直觉模糊集[5]的推广，能有效描述不确定性[6-10]. 单值中智集与三支决策的融合也被广泛研究[11-19]. 然而，如何建立基于不完备单值中智信息系统的三支决策模型，尚未有文献涉及.

    本文针对不完备单值中智信息系统. 首先，利用平均值法将不完备单值中智信息系统补全为完备单值中智信息系统；然后，基于补全的完备单值中智信息系统建立三支决策模型；最后，通过选择产品供应商的例子阐述新模型的应用，并详细分析了模型中参数变化对决策结果的影响.

1.   预备知识

  • 本节给出所需的一些基本概念.

    • 1.1.   单值中智集与单值中智数

  • 定义1[4]  设U是一个论域，U上的一个单值中智集Ã可表示为如下形式：

    其中：$\forall u \in U, T_{\tilde{A}}(u), I_{\tilde{A}}(u), F_{\tilde{A}}(u) \in[0,1], T_{\tilde{A}}(u), I_{\tilde{A}}(u) \text { 和 } F_{\tilde{A}}(u)$和$ F_A^{\sim}(u)$分别称为正确隶属函数、不确定隶属函数和错误隶属函数. 称三元组$ \left(T_A^{\sim}(u), I_A^{\sim}(u), F_A^{\sim}(u)\right)$为一个单值中智数，单值中智数p简写为$ p=\left(T_p, I_p, F_p\right)$，其中$ T_p, I_p, F_p \in[0, 1]$.

    定义2[10]   设p，q为两个单值中智数，k是一个大于0的实数，定义下面两个运算：

    1) $ p \oplus q=\left\langle T_p+T_q-T_p \cdot T_q, I_p \cdot I_q, F_p \cdot F_q\right\rangle ;$

    2) $ k p=\left\langle 1-\left(1-T_p\right)^k, \left(I_p\right)^k, \left(F_p\right)^k\right\rangle .$

    文献[9]指出了单值中智数排序方法的不足，并给出了单值中智数的一个新排序方法.

    定义3[9]  设p=(Tp，Ip，Fp)和q=(Tq，Iq，Fq)是两个单值中智数，

    1) 若sc(p) < sc(q)，则称p小于q，记作p≺q；2) 若sc(p)=sc(q)，ac(p) < ac(q)，则p≺q；3) 若sc(p)=sc(q)，ac(p)=ac(q)，Ip < Iq，则p≺q；4) 若sc(p)=sc(q)，ac(p)=ac(q)，Ip=Iq，则称p等于q，记作p=q，

    其中$ s c(p)=\frac{T_p+\left(1-F_p\right)}{2} \text { 和 } a c(p)=\frac{T_p}{T_p+\left(1-F_p\right)}$分别为p的得分函数和精确度函数.

    文献[9]证明了定义3中给出的排序方法可以比较任意两个单值中智数.

    • 1.2.   三支决策

  • 文献[1]基于贝叶斯决策理论阐述了三支决策的过程. 设U为非空有限集，R是U上的一个等价关系，$ [u]_R=\{v \in U \mid(u, v) \in R\}$是u的等价类. 设$ \mathit{\Psi}=\{C, \neg C\}$是状态集，$ \mathit{\Lambda}=\left\{\pi_P, \pi_B, \pi_N\right\}$，πN}是行动集，其中状态$ C \text { 和 } \neg C$分别表示对象属于C和不属于C，$ \pi_P, \pi_B, \pi_N$分别表示对u采取的3个行动，即决定$ u \in \mathit{POS}(C), u \in \mathit{BND}(C), u \in \mathit{NEG}(C)$. 损失函数是采取某种行动带来的损失，具体如表 1所示.

    在表 1中，γPP，γBP和γNP分别表示当对象u属于C时，采取πP，πB和πN这3种行为带来的损失；γPN，γBN和γNN分别表示当对象u不属于C时，采取πP，πB和πN这3种行为带来的损失，应满足条件γPP≤γBP≺γNP，γPN≤γBN≺γNN. 对每个对象采取3种不同行动的期望损失分别为：

    其中P(C|[u]R)和P(¬C|[u]R)分别表示等价类[u]R中的对象属于C和不属于C的条件概率.

    根据最小风险贝叶斯决策理论，得到如下决策规则：

2.   不完备单值中智信息下的三支决策模型

  • 本节将建立面向不完备单值中智信息的三支决策模型.具体的，将一个不完备单值中智信息系统补全为完备单值中智信息系统，然后基于补全的完备单值中智信息系统建立三支决策模型.

    定义4  单值中智信息系统是一个四元组(U，A，V，f)，其中U={u1，u2，…，un}为对象的非空有限集，A={a1，a2，…，an}为属性的非空有限集，V=∪a∈AVa，Va为a的属性值之集，f：U×A→V为信息函数，满足$ \forall u \in U, a \in A$，有f(u，a)∈Va，且f(u，a)是一个单值中智数.

    定义5  不完备单值中智信息系统是一个四元组(U，A，V，f*)，其中U为对象的非空有限集，A为属性的非空有限集，V=∪a∈AVa，Va为a的属性值之集，f*：U×A→V为信息函数，满足∀u∈U，a∈A，有f*(u，a)∈Va，且f*(u，a)为单值中智数，且至少存在一个(u，a)∈U×A使得f*(u，a)是一个含未知值的单值中智数.

    对于一个不完备单值中智信息系统，采用平均值法补全未知(缺失)值，即单值中智数中的未知值用该属性下其他对象的已知属性值的平均值代替，从而一个不完备单值中智信息系统可被补全为一个完备的单值中智信息系统，称之为由平均值法诱导的完备单值中智信息系统.

    例1  表 2所示是一个不完备单值中智信息系统(U，A，V，f*)，其中“*”表示该值未知. 利用平均值法，表 2被补全为一个完备的单值中智信息系统(见表 3).

    文献[8]提出了两个单值中智数之间的相似度如下：

    定义6[8]  设p=(Tp，Ip，Fp)和q=(Tq，Iq，Fq)是两个单值中智数，定义p和q之间的相似度为

    基于定义6，从不完备单值中智信息系统出发，基于诱导的完备单值中智信息系统给出对象间的相似度的定义.

    定义7  设(U，A，V，f*)是一个不完备单值中智信息系统，(U，A，V，fc)是由平均值法诱导的完备单值中智信息系统.∀u，v∈U，对象u和v的相似度定义为：

    其中#A表示A中属性的个数，Sai(u，v)=S(fc(u，ai)，fc(v，ai))是对象u和v关于属性ai的相似度.

    例2  (续例1)根据表 3和定义7，可得对象之间的相似度如下：

    进一步给出不完备单值中智信息系统中α相似关系和α相似类的定义.

    定义8  设(U，A，V，f*)是一个不完备单值中智信息系统，(U，A，V，fc)是由平均值法诱导的完备单值中智信息系统. ∀α∈[0, 1]，U上的α相似关系定义为：

    ∀u∈U，u关于α相似关系SRα的α相似类定义为：

    例3  (续例2)令α=0.4，根据定义8，可得α相似关系SRα如下：

    $ S R^{0.4}=\left\{\left(u_1, u_1\right), \left(u_1, u_2\right), \left(u_1, u_3\right), \left(u_2, u_1\right), \left(u_2, u_2\right), \left(u_2, u_3\right), \left(u_3, u_1\right), \left(u_3, u_2\right), \left(u_3, u_3\right), \left(u_4, u_4\right)\right\}$进一步，可得α相似类为：

    在三支决策理论框架下，结合定义3和决策准则(P)-(N)可得面向不完备单值中智信息的决策规则如下：

    $ \left(\mathrm{P}^*\right) \text { 若 } s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)<s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right), \operatorname{ac}\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)<a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right), \text { 或 }$

    $ s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)=a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right), I_{\mathrm{E} P}<I_{\mathrm{E}_B} ;$

    $ \text { 且 } s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^a\right)\right)<s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)<a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_p \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right)=a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^a\right)\right), I_{\mathrm{E}_p}<I_{\mathrm{E}_N};$

    $ \text { 则 } u \in P O S(C) \text {. }$

    $ \left(\mathrm{B}^*\right) \text { 若 } s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)<s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)<a c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)=a c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right), I_{\mathrm{E}_B}<I_{\mathrm{E} P};$

    $ \text { 且 } s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^a\right)\right)<s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^a\right)\right) \text {, 或 }$

    $s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)<a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right) \text {, 或 } $

    $ s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right)=a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right), I_{\mathrm{E}_B}<I_{\mathrm{E}_N} ;$

    $ \text { 则 } u \in B N D(C) \text {. }$

    $\left(\mathrm{N}^*\right) \text { 若 } s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)<s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right) \text {, 或 } $

    $ s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)<a c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^a\right)\right)=s c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^a\right)\right), a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^a\right)\right)=a c\left(\mathrm{E}\left(\pi_P \mid[u]_{S R}^a\right)\right), I_{\mathrm{EN}}<I_{\mathrm{E} P} ;$

    $ \text { 且 } s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)<s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)<a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right) \text {, 或 }$

    $ s c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)=s c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right), a c\left(\mathrm{E}\left(\pi_N \mid[u]_{S R}^\alpha\right)\right)=a c\left(\mathrm{E}\left(\pi_B \mid[u]_{S R}^\alpha\right)\right), I_{\mathrm{EN}}<I_{\mathrm{EB}};$

    $ \text { 则 } u \in N E G(C) \text {. }$

    其中

    本文提出的三支决策模型的关键步骤可总结为下面的算法1.

3.   模型的应用

  • 本节利用一个选择产品服务商的决策问题的例子，阐述面向不完备单值中智信息的三支决策模型的有效性和可行性.

    随着互联网的发展，数据变得尤为重要，越来越多的企业开始关注数字化转型，利用大数据技术为其服务. 为提高数据管理能力，某公司想要选择一个数据产品服务商. 设U={u1，u2，…，u10}为10个供应商，A={a1，a2，a3，a4}为4个条件属性(其中a1表示“产品质量”，a2表示“处理能力”，a3表示“售后服务”，a4表示“购买成本”)，D={d}为决策属性. 该领域的专家根据条件属性为每个供应商给出评价值，评价值为单值中智数. 由于某些原因，其中一些数据值是缺失的. 关于供应商的不完备单值中智信息系统如表 4所示，其中决策属性值d=1表示专家推荐该供应商，d=0表示专家不推荐该供应商. 下面利用本文提出的模型对10个供应商做出评判. 给定α=0.37.

    由表 4可以得到两个状态集：C={u3，u4，u6，u9}，¬C={u1，u2，u5，u7，u8，u10}. 它们分别代表推荐的供应商集合和不推荐的供应商集合. 损失函数如表 5所示，每个损失是一个单值中智数.

    按照算法1给出步骤如下：

    1) 将不完备单值中智信息系统补全为完备单值中智信息系统，如表 6所示.

    2) 根据表 6计算对象关于属性ai(i=1，2，3，4)的相似度Sai(u，v)，这里仅展示Sa1(u，v) (表 7).

    3) 计算对象间的相似度Sim(u，v)(表 8).

    4) 由定义8可得对象的相似类：

    计算条件概率P(C|[u]SR0.37)如下

    5) 计算期望损失(表 9).

    6) 计算期望损失的得分函数和精确度函数(表 10).

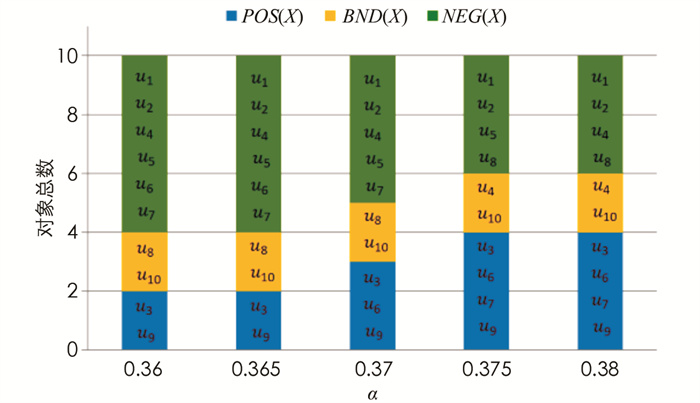
    7) 根据准则(P*)-(N*)，可得三支决策结果：

    a) u3，u6，u9∈POS(C)；

    b) u8，u10∈BND(C)；

    c) u1，u2，u4，u5，u7∈NEG(C).

    根据上述决策结果，建议该公司选择供应商u3，u6或u9；同时，供应商u8和u10需要进一步考虑；而供应商u1，u2，u4，u5和u7则不太合适.

4.   参数变化对决策结果的影响分析

  • 本节讨论参数α变化对模型的影响分析.选取α=0.36，0.365，0.37，0.375，0.38，损失函数的得分函数和精确度函数的结果分别展示在表 10-14中. α不同取值产生的决策结果如图 1所示.

    由图 1可看出，随着α的增大，被划分到正域的对象增多. 对于决策者来说，选择不同的α，意味着产生不同的决策结果. 在处理实际问题时，需要根据实际情况具体分析，以选取最适合的α.

5.   结语

  • 本文研究了不完备单值中智信息下的三支决策模型. 将不完备单值中智信息系统补全为完备的单值中智信息系统，基于补全的完备单值中智信息系统计算对象间的相似度，进一步建立三支决策模型. 最后，利用选择产品供应商的例子阐述了模型的应用，并对模型中的参数进行了敏感性分析. 本文没有考虑信息表动态变化的情形，不完备动态单值中智信息下的三支决策模型是一个有意义的研究课题.

参考文献 (19)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回