-
在机器人感知领域中,对视觉信息的关注程度越来越高,其中同时定位与地图构建算法是该领域的重要方向. SLAM能够在没有任何先验信息的情况下,通过摄像机或激光雷达等传感器采集环境信息,来估计自身的运动模型和构建所处的环境地图,在智能飞行器、智能手机、机器人和AR/VR设备中,SLAM是不可或缺的底层支持算法,通过快速实时的运算和估计,不仅能使设备与环境更加深入的交互,更有利于顶层应用广泛而高效的开发.所以,科研技术人员一直在追求更加有效和快速的方法来实现SLAM.近年来,人们在SLAM领域取得了重大进展,例如,在视觉SLAM方面(Visual SLAM),最著名的ORB-SLAM就是一种基于特征点的SLAM系统[1],ORB-SLAM通过提取采集的图像的特征点进行帧间特征匹配,进而采取非线性优化完成相机位姿的估计,从而实现了自定位功能.进一步,PL-SLAM[2]在ORB-SLAM基础上引入了特征线,使系统在低纹理场景下更具鲁棒性.除此之外,经典SLAM还包括基于扩展卡尔曼滤波的MSCKF[3],基于单目相机的MonoSLAM[4],与特征点不同的直接法匹配系统LSD-SLAM[5],以及加入了IMU惯性传感器的融合算法OKVIS[6],ROVIO[7],VIORB[8]等等.这些SLAM算法主要优化了位姿和稀疏地图点,因在优化过程中忽略了误差较大的地图点,所以并不能形成真正用于导航和场景理解的地图.因此,从实际情况来看,仅凭稀疏地图点以及机器人的行动轨迹并不能完整地构建导航地图,也无法有效地进行机器人避障与自主探索.在建图方面,算法RGBD-SLAM[9]通过利用较为可靠的深度信息提高了传统迭代最近点算法(Iterative Closest Point,ICP)的精度和鲁棒性.然而,以上算法仍然忽略了误差较大的地图点,而通过实践发现部分特征点来自场景里的动态事物投影点,因此这些无法识别的动态障碍物将会影响机器人的导航和避障[10-12].
在SLAM系统的静态场景建图方面,常采用简单的点云构图[13],即通过传感器模型(Sensor Model,SM)求得空间点云,网格化后生成体素,从而形成点云体素占有地图.然而该算法消耗的计算资源非常大且不利于地图的维护,尤其是在大规模场景重建的情况下效率非常低,为了提高效率,就需要计算各个网格的占有概率. Dia和Mottin提出了一种应用于一维至三维的基于逆传感器模型的概率网格地图算法[14],这种算法为地图的实时更新提供了可能.进一步,在概率网格地图的基础上发展出了应用最为广泛的建图方法是Hornung提出的八叉树地图OctoMap[15],利用八叉树数据结构作为基础,压缩了点云地图的存储,同时进行网格占用概率的估计,与WHELAN T等[16]的点云建图方法相比大范围提高了建图的效率,减少了存储空间的消耗.然而,为了能够高效应用于计算能力较差或存储容量较低的终端,作为底层支持算法的SLAM希望构建的是更加小巧便捷的地图.对于树状数据结构而言,比八叉树更精简的是四叉树,四叉树的节点数量接近八叉树的二分之一.而目前的研究中四叉树常见于激光雷达SLAM算法,由于激光雷达进行的是平面二维扫描,因此获得的场景信息极为有限,为此,本文重点研究了视觉SLAM中的四叉树建图算法.
在实际的室内环境中,视野中的动态事物能够被传感器捕捉,因此动态事物的运动方向以及运动状态会影响机器人的导航,被称之为“交通管制问题”.交通管制问题使机器人的定位与建图功能受到限制,甚至可能导致无法完成可靠的避障、路径规划与自主探索.为此,文献[17]通过深度学习的方法实现了常见室内事物的语义识别,并赋予其现实含义,进而提出了基于语义识别的SLAM算法.但是,该方法的图像多目标识别的效果有限,且运算复杂度较高,因此,较难应用于机器人的基础底层定位建图.
本文在ORB-SLAM系统上进行改进,首先在补充点云数据进行稠密重建的基础上对三维点云进行完全的地面二维投影,通过该降维运算,构建携带三维信息的二维导航地图,并利用四叉树结构进行储存,相比于八叉树三维地图,本文的二维建图方法能够高效实现更大规模的可靠建图.在机器人的实际运行过程中,对偏差较大的特征点创建动态矢量,并对其利用改进的K-means算法进行分析判断,从而识别出动态障碍物矢量;在两帧之间推测出动态障碍物的行动方向和速度,进而在概率表示的网格地图中完成标识,为机器人实时自动导航提供动态障碍物的可靠信息.最后,采用安装了RGBD相机的室内移动机器人对本文算法进行实际测试,实验结果表明:本文的二维建图算法能够在动态室内场景中实现精准的自定位与环境地图重建,所得的二维导航地图占用极小的空间,在未使用深度学习的条件下能够提供丰富的环境语义信息,实现机器人的自主导航和避障.
全文HTML
-
本节介绍和推导本文采用的数学模型.主要包括ORB-SLAM的建模方法和优化方法,概率网格地图的构建模型,地面提取的随机抽样一致(Random Sample Consensus,RANSAC)算法,点云投影变换算法以及四叉树地图储存的相关算法,利用这些数学模型,构建基于四叉树的二维网格建图模型.
-
ORB-SLAM算法采用光束平差法(Bundle Adjustment)优化机器人定位信息.首先建立像素点与空间点的相机的传感器模型:
其中z指的是像素深度值,pu,v指代图像像素坐标,K为相机内参数矩阵,T为位姿,Pw为世界坐标.
将公式(1)表示成s=h(x,y),这里观测量s即公式(1)中的pu,v,(x,y)分别代表了位姿T和地图点Pw.引入传感器观测误差e=s-h(x,y),即相机观测以及标定误差. ORB-SLAM因采用非线性图优化方法因此无需关注噪声类型.在系统运行时,图像随着时间不断加入系统,累积的状态采用(x1,x2,…,xm,y1,y2,…,yn)表示,因每一帧包含大量观测的地图点,因此y的数量远大于x的数量,即m≫n.建立代价函数:
对xi和yi进行一阶泰勒展开:
其中,Fi,j和Ei,j为雅可比矩阵.
利用高斯牛顿法对上式进行优化.在优化时,ORB-SLAM对该代价函数的大误差项用Huber回归损失函数进行线性替换,以消除大误差项对优化造成的影响,即
其中,δ为误差阈值.当误差超过该阈值,将采用Huber函数进行滤波.从公式(4)可以看到,将误差较大的项在公式(2)的累加方程中以一次函数替换,减少了二范数增长过快对优化效果的影响.而在公式(2)中大误差来源于位姿值和地图点位置的不匹配,主要包括两帧图像之间特征点的误匹配和从动态障碍物提取了特征点两种情况.对于机器人自定位来说,这种误差点均需要消除,但是对于动态场景的地图构建,由于需要捕获动态障碍物特征点的移动方向,大误差点却是非常重要的计算参量.
-
与Huber函数不同,随机抽样一致算法[18]在ORB-SLAM中主要用于误匹配消除.该算法主要在数据集中选取子集并拟合函数,即计算子集外的元素与子集拟合的函数的相关性,若相关性高则子集拟合可以近似替代数据集拟合;若相关性低则再次选取新的子集.迭代上述过程直到选取的子集最能拟合数据集内大多数元素为止,即可理解成为最符合整个样本空间的拟合函数.
-
机器人在进行自定位后,将位姿与图像数据传入建图程序进行同步建图,建图算法基于的是贝叶斯后验概率模型.机器人处在室内静态环境中,通过视觉传感器数学模型建立外部环境.考虑到传感器存在噪声的影响,此类不确定因素的概率分布模型称为概率传感器模型(Sensor Model,SM).而在检测到外部信息的数据后,通过外部数据建立地图和动态障碍物的模型称为逆传感器模型(Inverse Sensor Model,ISM)[14].首先定义建立的地图网格之间相互独立.假定Ω表示三维空间,并定义为空间参考系(Spatial Reference),N为网格的个数,i为网格下标,c为网格基础单元,mi为二元随机变量. mi表示了c的占有概率. mi∈(oi,ei),即oi和ei分别表示占有和空白两种情况,由于表示网格单元是否占有的随机变量具有互斥特性,因此:
对于地图的概率分布可由全部网格单元概率累乘求出:
利用传感器的输入数据求解的地图概率分布可由公式(6)展开:
其中,s是传感器的观测值,x是运动模型数据(即机器人的位姿).在给定传感器测量值s1:t和位姿数据x1:t时,每个单元mi的占有概率oi可根据t时刻及之前的观测值和运动模型由马尔可夫特性和贝叶斯准则计算得出:
同理,相同网格单元的非占有概率p(ei|s1:t,x1:t)与公式(8)的形式一致.根据公式(5)的关系将单元占有概率和非占有概率的比值进行计算,可得:
其中,等号左边的分母是由式(5)可得.再利用对数变换公式将式(9)重写为
利用公式(10)在SLAM系统运行时迭代计算每一个网格单元的占有概率,等式右边的第一项即为逆传感器概率模型,第二项为迭代项,第三项为传感器模型.由于RGB-D相机采集的点云是投影于三维空间
${s_t} \in {\mathbb{R}^3}$ 上的,故需对其进行二维投影操作,将三维空间点云投影至以地面为基准的二维地图上(本文假设室内环境的地面是理想平面).首先本文设置了两个高度阈值下高度阈值hdown和上高度阈值hup.对于机器人二维导航而言,过高的障碍物可以忽略,因此在hup以上的点云在处理中将会剔除,从而大量减少建图需要处理的地图点.下高度阈值是为了消除地平面法向量提取误差而设置的缓冲区.设$g \in {\mathbb{R}^2}$ 为地面参考系,表示为相对于初始相机位姿的变换矩阵Tg.设pg为二维网格单元,则二维地图点观测值投影为其中,f函数表示从三维点投影到二维点映射.由公式(12)可知,f函数在投影过程中可能在二维网格地图上产生重合点,这是由多个三维单元重叠投影到同一二维地图区域上引起的.虽然投影得到的二维地图单元混合了传感器噪声,但是,本文不对此噪声进行处理,而是在工程上采用点云的降采样滤波.
进一步,对三维体素的概率进行投影生成二维网格占有概率:
投影后即可生成二维网格的逆传感器占有概率模型.通过将视觉三维传感器模型转化成二维传感器模型,减少了大量三维体素的概率计算,提高了效率.
-
对于三维空间数据的二维投影需要基准平面,以地面为基准,而对于地平面提取与世界坐标系的构建在SLAM建图领域一直被忽视.在地面机器人SLAM算法与稠密建图中,以地平面的视野扩张方向作为相机位姿调整的基准更加适合二维网格建图.目前,SLAM算法中通常以相机的初始位姿作为世界参考系的原点和轴向.本文首先计算地平面相机初始位姿与地平面的姿态矫正矩阵,该矩阵代表了从相机初始位姿参考系到地面参考系的变换,并作为二维建图的基准进行系统初始化.设Tg为变换矩阵,Pmark为初始化标志物,该标志物由一条容易提取特征点的三角形构成,平置于相机初始视野内的地面上,利用一致性拟合算法RANSAC拟合地平面:
1) 从RGBD相机初始帧抓取的点云图中提取地面标志物点云.
2) 设定地面方程公式为Ax+By+Cz=D和误差值,随机抽选3个点进行平面构建,计算其他点云是否在误差内满足该平面公式,记录内点和外点个数.
3) 重复循环第二步,直到选出大多数点满足误差内的平面公式,取出该平面的A,B,C值形成地平面法向量.
可见,RANSAC算法的迭代次数较多,因此,该算法只在第一帧初始化或机器人视野中再次出现Pmark的情况下求解变换矩阵,避免大量的迭代计算.
根据地平面法向量计算原相机坐标系(世界坐标系)到地平面坐标系的变换矩阵Tg:
其中,四元数qx和qy表示旋转.将世界坐标系的z轴调整至与地平面法向量一致,则无需进行平移和x与y轴的变换.因此,通过公式(13)和公式(14)即可得出Tg,该地平面变换矩阵可将世界坐标系中的地图点转化成为地面坐标系的地图点.
-
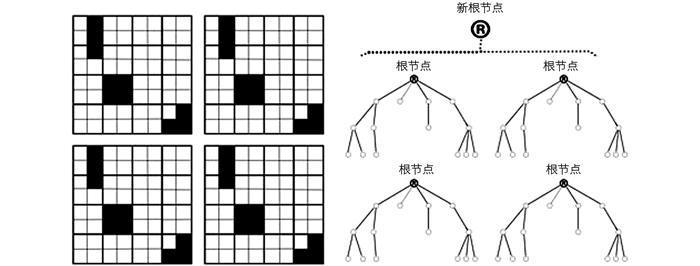
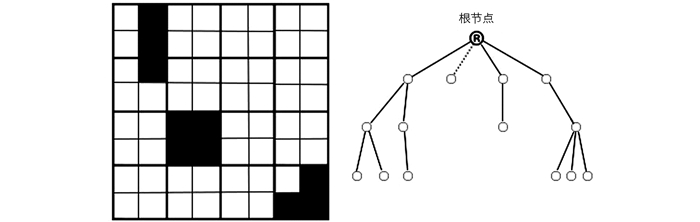
最后,对投影产生的二维地图数据采用四叉树数据结构保存,可提高地图的存储和搜索的效率.文献[15]的八叉树结构是针对三维空间数据构建的,所需的节点数是四叉树的两倍.二维地图由于将三维空间点投影至二维平面点,且对投影重叠部分进行了数据降采样滤波,减少了大量的无关地图点,因此,更适用于场景的大规模建图.四叉树结构如图 1所示.从图 1可知对于64单元的网格地图存储仅需要14个节点,与点云数据和八叉树相比节省了大量的储存空间.
本文对地图的四叉树存储采用动态方法,如图 2,每一帧都以四叉树形式保存,当有新的图像帧加入系统,会生长出新的四叉树.当4个四叉树数据结构匹配后会整合成新的四叉树,更新根节点和叶子节点,其中保存的网格占有概率会实时更新.设定网格分辨率,以占据网格的初始概率为0.9,空闲网格的初始概率为0.1,在初始帧情况下建立视野区域并按照网格分辨率分割.根据相机初始位姿加首帧二维投影观测值,计算每个网格是否占有,占有则概率值为0.9,否则概率值为0.1.进一步,利用式(10)和式(13)迭代更新其占有、空闲概率值,如果占有概率值达到0.9则视为占有网格,若空闲概率低于0.1则设为空闲概率,未更新的区域占有概率设为0.5,表示其网格的状态为未知情况.占有概率的运算是对概率值的对数变换进行运算,保存在节点中的值也是对数值,将节点值进行反对数变换后即可得到真正的占有概率.通过对数变换,可将乘除运算转化为加减运算.公式(16)为t时刻的地图概率状态的对数更新.
其中,log9是观测到占有情况加上的量,log4是观测到空闲情况减去的量,通过对之前的概率进行更新,即可迭代计算每个网格在观测情况下的概率值.
建立生长型四叉树数据结构对二维网格地图进行储存,系统每加入一帧图像关键帧,则更新现有四叉树叶子节点的节点资料,并根据新加入的地图点方向构建与上一帧独立的新的四叉树数据结构.创建栈数据结构,其中存在一个初始四叉树,将新的四叉树压栈,如图 2所示,当匹配到4个相关树时将该栈释放,并设置根节点形成新的四叉树同时更新所有叶节点资料.将新的四叉树压入新栈,树的深度加1.当形成更深的四叉树时意味着二维地图在生长扩大.
1.1. ORB-SLAM的优化模型构建
1.1.1. 随机抽样一致算法
1.2. 空间网格地图的概率模型构建
1.3. 地平面投影变换与地面坐标初始化
1.4. 生长型四叉树数据结构
-
ORB-SLAM系统在特征点提取方面划分了视野网格,将采集的图像设置成64*48个区域,目的在于保证从视野中均匀地提取特征点,这使得视野中存在动态障碍物时,容易获取动态障碍物区域的ORB特征点.而在ORB-SLAM系统中,大误差点会被Huber函数降幂替换,除了Huber函数,应用在单目单应矩阵计算的RANSAC算法也会将误差点进行剔除,而被剔除的大误差特征点在实践中有一部分是从动态障碍物体上提取的.
此外,大误差点除了来自动态障碍物之外,还有一个重要的来源是两帧图像的特征点误匹配. Sift特征提取算法[19]的特征信息丰富,对于旋转、视角变换、光线变化等都具有较好的匹配效果,是目前最准确的特征提取算法.然而由于Sift算法计算量大且计算要求较高,因此难以在计算能力有限的设备上完成实时运算.基于此,本文的方法不改变ORB-SLAM原有的提取模式,首先对可能出现的所有误匹配点进行其动态矢量的计算,接着重点对动态矢量进行处理,动态矢量的公式如下:
其中,Vec为动态障碍物运动方向,i为动态障碍物索引,Pw表示特征点的世界坐标,t为时间帧索引.
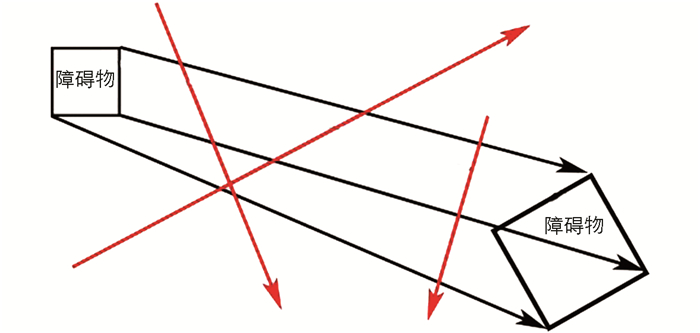
本文利用了改进后的K-means进行动态障碍物矢量的提取,剔除误匹配点.从几何上进行分析,如图 3所示,同一障碍物上的多个特征点同时误匹配的概率低于单一特征点的误匹配概率.因此将公式(17)求出的大量动态矢量作为输入,利用矢量的相似性指标,通过聚类算法求解动态障碍物矢量集合.
图 3中的左右方格是同一个障碍物的两帧位姿,反映到障碍物的特征点矢量即为图中黑色的向量,相对的特征点误匹配矢量则为红色向量.本文利用了K-means聚类算法对动态矢量进行聚类提取出动态障碍物矢量,并结合相机对应的位姿数据,求得动态障碍物的速度和移动方向,这里的速度是根据网格地图分辨率来计算的网格速度,即为曼哈顿距离与帧间时差的比值.另需要说明矢量的相似性聚类是通过两步进行的,第一步是聚类矢量的起始点,利用选取欧氏距离作为相似度指标的K-means聚类算法将起始点相近的矢量聚成一类;第二步则对第一步中聚类而来的集合再进行以矢量投影作为相似度指标的聚类,这需将K-means算法的迭代公式改为
根据公式(18)将矢量聚类:随机选取向量bk,计算剩余向量ai与选取向量之间的投影,再求投影值与选取向量之间的差值.考虑到矢量投影可能大于被投影矢量,因此补充幂运算求该差值的平方.经迭代,从起始点聚类的集合中得到动态障碍物矢量的聚类结果,并计算其平均值,此即为动态障碍物的移动矢量,该移动矢量将被用于导航算法.
-
由于在系统运行中,动态障碍物的信息变动较大,变动速度较快,因此不适合直接对生长四叉树的节点进行添加删除和更新操作.为了避免频繁搜索和读写四叉树节点,新建数组结构,专门存储动态障碍物信息,该数组集合通过索引与四叉树网格地图建立联系,将障碍物矢量起点和终点的位置经过地面坐标系变换以及二维网格地图投影后存入障碍物数组,该矢量信息可用于机器人的自主导航的动态避障工作[20-21].
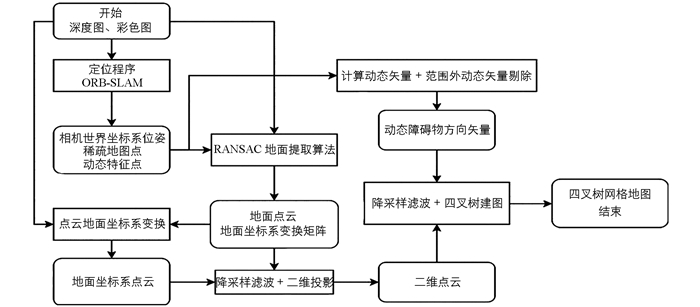
最后,将基于生长四叉树结构的二维建图算法流程图总结如图 4所示.
2.1. 动态障碍物识别
2.2. 二维网格地图的动态障碍物概率叠加
-
建图实验利用了搭载Kinect.v1深度摄像机(RGB-D Camera)的小强机器人.小强机器人集成了运动模块和驱动程序,可以进行自主的地图探索,如图 5所示.深度摄像机由彩色摄像机和一个深度传感器构成,可以发射红外结构光,用于深度信息的测量.代码基于ORB-SLAMv2的RGB-D版本[1]开发,无需进行对极几何和极线搜索的运算.
为了比较本文二维投影四叉树建图与八叉树建图的效率和存储空间消耗,设置一项对比试验,选取nyud数据集dining_room序列中的5帧图像,对其进行八叉树三维重建和四叉树二维重建,对比两者的运行时间、树结构节点数和存储空间消耗数据,从而比较二者算法的性能优劣.对不同分辨率选取进行了实验,讨论分辨率选择对建图效果的影响.对地面提取进行误差实验,讨论地面法向量提取误差对下高度阈值选择的影响.
最后应用小强机器人在实际室内场景中运行ORB-SLAM2和三维稠密点云的二维投影四叉树建图程序,验证本文方法的实际运行效果.
-
图 6(a)显示了ORB-SLAM在室内环境下的稀疏建图,从该图中可知稀疏地图点信息量较少,不能获得准确的障碍物信息,因此无法利用稀疏点地图进行有效导航. 图 6(b)显示了环境的稠密三维点云图,从该图可知该地图缺乏地面提取的信息.因此,将图 6(b)经过地面坐标变换投影后生成二维点云图,如图 6(c)所示.由图 6(c)可知,二维投影点云图能够较好地提取真实场景中障碍物的信息和机器人导航中所需的地面信息,因此,基于二维点云图生成的地图能够有效地应用于机器人导航.
图 7所示为体素地图和网格地图.网格地图相较于体素地图缺少了高度维,但是在实际SLAM程序中,可以通过设置阈值来使一定高度范围内的障碍物投影,因此即使地图缺少高度维数据,二维网格地图对于地面机器人导航仍然具备理论上的可靠性.
表 1显示了八叉树与四叉树在不同分辨率下的速度与容量对比.分辨率越高的意味着在SLAM系统中建图范围越广,地图容量就会越大.从表 1可以看出四叉树建图的地图容量远小于八叉树地图,建图速度也同样远高于八叉树建图. 表 2显示了不同场景下3种地图模式的性能比较,从表中可知四叉树投影地图的性能要优于八叉树地图,树的深度一致是由于树深度取决于地图范围,而四叉树的节点数是八叉树的一半.对于室内地面机器人而言,本文的三维视觉投影二维四叉树地图更加适用于视觉SLAM系统.
在投影过程中,上高度阈值是投影障碍物的上限,在阈值以上的障碍物假定为对自主导航无影响障碍物,因此不对其进行投影.下高度阈值是对地面提取误差的修正,在地面提取有误差的情况下,下高度阈值太低会造成将部分地面也投影成障碍物,影响机器人的导航判断,高度太高则会忽略实际障碍物的投影,法向量对高度阈值的影响如图 8所示,这里假设场景地面范围为300,法向量偏差值为0-π/4(0-0.79),下高度阈值根据偏差来进行设置,当偏差过大,需要重新验证地面的提取是否可靠,偏差较大需要对法向量提取过程进行噪声滤波.
图 9显示了小强机器人结合ORB-SLAM和三维重建程序的实际室内场景运行效果,建图采用了ROS的Rviz三维可视化平台[22]显示.建图程序将视野中提取的三维障碍物投影至二维网格地图建立了可导航地图.白色代表了可行区域,黑色代表了障碍物,灰色是未知网格单元.从图(9)左中可见,本文提出的四叉树建图算法具有较高场景环境的重建精度,但由于缺乏对四叉树概率值进行动态调整,导致概率地图的误差累积,因此,图像中间和右边仍然存在少部分的错误障碍物投影.
3.1. 八叉树建图与投影四叉树建图
-
针对传统SLAM无法建立高效可导航地图的缺点,本文在ORB-SLAM和八叉树建图的基础上,建立了基于四叉树的二维投影网格地图算法,与八叉树地图和点云地图相比,四叉树建图算法大量降低了地图存储空间,提高了建图速度,适合地图的大规模重建.实验结果表明:基于四叉树的二维网格建图算法能够高效地应用于室内地面机器人的场景地图重建和自主导航,由于本文算法有效地处理了动态障碍物,因此能够为机器人自主导航提供更加丰富的语义信息,具有较强的实用性,能够实时生成用于机器人自主导航和路径规划的地图.



 下载:
下载: