-
近年来人体内肿瘤与免疫系统之间的相互关系逐渐成为研究的热点问题,其中借助数学动力学模型来研究二者随时间演化的动力学性态成为一条重要的研究途径[1].特别地,文献[2]将免疫系统分为两个子类,即狩猎细胞(细胞毒性T淋巴细胞)和静息细胞(T辅助细胞),并借助经典捕食-食饵模型研究了肿瘤与免疫细胞的相互关系.考虑到静息细胞向狩猎细胞的转化需要时间,文献[3-4]在文献[2]的基础上研究了转化时滞对系统动力学性态的影响,发现时滞可能会使系统产生周期解.文献[3-4]考虑的是离散时滞,即假设转化时间是一个固定的常数.若假设转化时间在某一个值附近波动,则考虑分布时滞会更加准确[5].
同时,由于单靠人体自身免疫往往无法消除肿瘤,因此在肿瘤免疫系统中考虑各种治疗并研究其效果是非常有意义的.当前常用的治疗方法有化疗、免疫治疗及放射治疗[6-8].本文在文献[2]的基础上同时考虑化疗、免疫治疗及分布时滞得到如下动力学模型:
其中:M(t),N(t),Z(t)分别表示t时刻肿瘤细胞、狩猎细胞(CTL细胞)、静息细胞(辅助性T细胞)的数量;U(t)表示药物的浓度;r1和r2分别为肿瘤细胞和静息细胞的内禀生长率;α为狩猎细胞对肿瘤细胞的杀灭率;β1和β2为静息细胞向狩猎细胞的转化率;bi(i=1,2)为环境容纳量;di(i=1,2,3)为相应细胞死亡率及药物的衰减率;p为辅助性T细胞外部免疫输入率,代表免疫治疗的强度;v为化学药物的输入率,ai(i=1,2,3)为化疗药物对相应细胞的杀伤率.本文假设静息细胞向狩猎细胞的转化时间依概率密度函数k(s)分布,满足k(s)≥0且
$\int_0^\infty k (s){\rm{d}}s = 1$ .
全文HTML
-
首先讨论系统(1)平衡点的存在性.定义
则可得如下定理1.
定理1 系统(1)的平衡点存在性情况如下:
(ⅰ)系统总存在无肿瘤-无免疫平衡点E1=(0,0,Z1,U1),其中
(ⅱ)若a1 < a1*成立,则存在无免疫平衡点E2=(M2,0,Z2,U2),其中
(ⅲ)若p>p*成立,则存在无肿瘤平衡点E3=(0,N3,Z3,U3),其中
(ⅳ)若a1 < a1**,p>p*成立,则存在共存平衡点E4=(M4,N4,Z4,U4),其中
证 这里仅证明无肿瘤平衡点E3和共存平衡点E4的存在性.令系统(1)中的4个等式右边为零,则得到以下方程组:
由方程组(2)第4个等式解出
${U_3} = \frac{v}{{{d_3}}}$ ,代入第2个等式得到${Z_3} = \frac{{{d_1}{d_3} + {a_2}v}}{{{\beta _1}{d_3}}}$ ,进而由第3个等式可得显然Z3>0,U3>0.注意到
知此时存在无肿瘤平衡点E3.
若共存平衡点E4存在,显然N4=N3,Z4=Z3,U4=U3.将N4,Z4,U4代入方程组(2)的第一个等式,计算得
注意到
知此时存在共存平衡点E4.定理证毕.
-
首先讨论时滞为零的情况,此时系统(1)变为如下常微分方程:
由于时滞不改变平衡点的存在性,计算系统(3)在平衡点Ei(i=1,2,3,4)处的雅可比矩阵得:
其中Ai=r1-2r1b1Mi-αNi-a1Ui,Bi=β1Zi-d1-a2Ui,
${C_i} = - {r_2}{b_2}{Z_i} - \frac{p}{{{Z_i}}}$ .则系统(3)在平衡点Ei(i=1,2,3,4)处的特征方程为从而可得如下定理2.
定理2 系统(3)各平衡点稳定性情况如下:
(ⅰ)如果a1>a1*,p < p*成立,则无肿瘤-无免疫平衡点E1局部渐近稳定;
(ⅱ)假设a1 < a1*.如果p < p*成立,则无免疫平衡点E2局部渐近稳定;
(ⅲ)假设p>p*.如果a1>a1**成立,则无肿瘤平衡点E3局部渐近稳定;
(ⅳ)若共存平衡点E4存在,即a1 < a1**,p>p*成立,则必然局部渐近稳定.
证 (ⅰ)对无肿瘤-无免疫平衡点E1=(0,0,Z1,U1),由(4)式可得对应的特征值分别为:
显然λ1 < 0,λ2 < 0.如果a1>a1*成立,有λ3 < 0.注意到
从而当p < p*时λ4 < 0,E1局部渐近稳定.
(ⅱ)对无免疫平衡点E2=(M2,0,Z2,U2),由(4)式可得对应的特征值分别为:
显然λ1 < 0,λ2 < 0,λ3 < 0.从而当p < p*成立时,λ4 < 0,E2局部渐近稳定.
(ⅲ)对无肿瘤平衡点E3=(0,N3,Z3,U3),由(4)式可得对应的特征方程为:
则有特征值λ1=-d3,λ2= r1-αN3-a1U3. λ3,λ4是下列二次方程的两个根:
显然λ1 < 0.注意到
知λ3,λ4一定有负实部.从而当λ2 < 0,即r1-αN3-a1U3 < 0或a1>a1**时E3局部渐近稳定.
(ⅳ)对共存平衡点E4=(M4,N4,Z4,U4),由(4)式可得对应的特征方程为:
则系统(3)在E4处的特征值分别为λ1=-d3,λ2= -r1b1M4,λ3,λ4是下列二次方程的两个根:
显然λ1 < 0,λ2 < 0.注意到
知λ3,λ4一定有负实部,从而只要共存平衡点E4存在则局部渐近稳定.定理证毕.
定理3 系统(3)任意两个平衡点不可能同时稳定.
证 若无肿瘤-无免疫平衡点E1局部渐近稳定,即有a1>a1*,p < p*成立,此时E2,E3,E4不存在.因此平衡点E1不可能与其他平衡点同时稳定.若无免疫平衡点E2存在且局部渐近稳定,即有a1 < a1*,p < p*成立,则此时E3,E4不存在,因此平衡点E2不可能与其他平衡点同时稳定.若无肿瘤平衡点E3存在且局部渐近稳定,即有p>p*,a1>a1**成立,此时E4不存在,因此E3,E4不可能同时稳定.定理证毕.
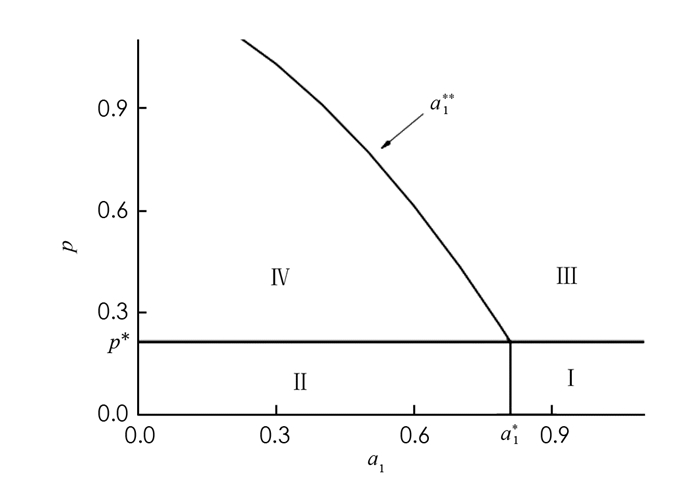
注 对系统(3)容易证明如果a1>a1*,则M(t)→0(t→∞),从而知只要化疗效果足够好,即化疗效应参数满足a1>a1*,则肿瘤细胞一定会被清除掉. 图 1为系统(3)在a1-p参数平面上的分支图,其中区域Ⅰ,Ⅱ和Ⅲ分别表示无肿瘤-无免疫平衡点E1、无免疫平衡点E2、无肿瘤平衡点E3的稳定区域;区域Ⅳ表示共存平衡点E4的稳定区域.再由定理2和定理3可知,如果要在免疫细胞持续生存的条件下清除掉肿瘤细胞,需要在保证化疗效果较好的前提(a1>a1**)下加大免疫治疗使得免疫治疗输入参数满足p>p*(见图 1参数区域Ⅲ).当免疫治疗强度较大,化疗效果较小,即a1 < a1**,p>p*时,肿瘤与免疫细胞可能共存(见图 1参数区域Ⅳ).
1.1. 平衡点的存在性
1.2. 平衡点的稳定性
-
本节考虑分布时滞对平衡点稳定性的影响.取核函数为弱核,即k(s)=me-ms,m>0,则
$\frac{1}{m}$ 为平均时滞.引入新的变量此时系统(1)变为如下等价的常微分方程:
系统(3)的共存平衡点等价于系统(5)的正平衡点E*=(M4,N4,Z4,Y4,U4),其中Y4=Z4.
讨论系统(5)正平衡点E*的稳定性.计算E*处的雅可比矩阵得:
从而可得特征方程如下:
定义
则可得如下结论.
定理4 (ⅰ)若mcr≤0,则正平衡点E*对所有时滞都局部渐近稳定.
(ⅱ)若mcr>0,则当m>mcr时,正平衡点E*局部渐近稳定;当0 < m < mcr时,正平衡点E*不稳定,且在m=mcr处发生Hopf分支.
证 由(6)式可得系统在正平衡点E*处有特征值λ1=-d3 < 0,λ2=-r1b1M4 < 0,其余特征值为下列三次方程的3个根:
其中
注意到L2(m)>0,L3(m)>0.由赫尔维兹判据可知,3个根都具有负实部,即E*局部渐近稳定的充要条件是
代入Li(m)(i=1,2,3)计算可得:
若mcr≤0,则Q(m)>0对所有的m>0成立;若mcr>0,则
从而知:若mcr≤0,则正平衡点E*对所有时滞都局部渐近稳定;若mcr>0,则当m>mcr时正平衡点E*局部渐近稳定,当0 < m < mcr时E*不稳定,当m=mcr时Q(mcr)=0,易知特征方程(6)有一对纯虚根.接下来由文献[9]知只需验证Hopf分支发生的横截条件.由(7)式可以得到:
从而由文献[9]知,系统(5)在m=mcr处发生Hopf分支.
-
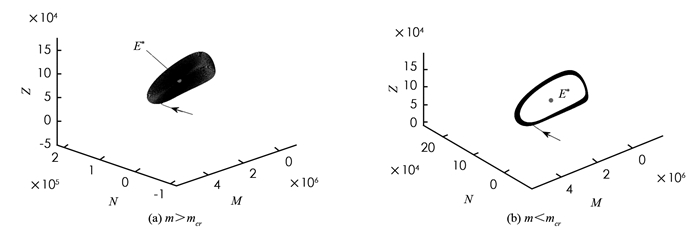
我们取定一组参数,r1=1.1,r2=0.06,b1=2×10-7,b2=1×10-7,β1=6.2×10-7,β2=5×10-7,α=1.101×10-5,p=0.3,v=0.8,d1=0.041 2,d2=0.01,d3=0.9,a1=0.1,a2=0.02,a3=0.02,则可以得到系统(5)正平衡点E*=(1.427 6×106,6.330 9×104,9.512 5×104,9.512 5×104,0.888 9).通过计算可得mcr=3.284 1,取m=5,则此时正平衡点E*是局部渐近稳定的;取m=3.1,则此时正平衡点E*不稳定. 图 2是系统(5)的相图,从中可以看到平均时滞比较小时,即当m>mcr时,正平衡点E*是一个稳定的焦点;当平均时滞增加越过一个阈值,即当m < mcr时,正平衡点E*不稳定,系统在E*附近通过Hopf分支产生周期解.从而可知分布时滞的引入可能导致系统产生周期震荡现象,进而可以解释肿瘤的复发现象.



 下载:
下载: