-
文献[1-3]表明基因改造蚊子是预防和控制蚊媒疾病的有效武器.文献[4-5]中提出重组后的工程共生细菌,标记为Serratia AS1.他们观察到蚊子在交配过程中,Serratia AS1细菌可以从携带细菌的蚊子转移到未携带的蚊子身上,并且Serratia AS1细菌可以附着在产下的卵上,并被从这些卵中孵化出来的幼虫吞食,随后附着在这些幼虫体内并在幼蚊中被大量繁殖,这些现象说明Serratia AS1细菌不仅可以在蚊子种群中水平传播,也可以垂直传播到下一代.此外,Serratia AS1细菌对蚊子的寿命和繁殖力没有明显的负面影响.因此,我们考虑将蚊子通过生物方法使其携带Serratia AS1细菌,来控制疾病的传播.
文献[6-8]建立了在离散时间、连续时间下转基因细菌在蚊子种群中传播行为的数学模型,为以后研究转基因细菌在蚊子中的传播行为的相关数学模型奠定了基础,但仅考虑了转基因细菌可以从携带细菌的幼蚊转到未携带细菌的幼蚊,没有考虑细菌在成蚊之间的传播.本文的Serratia AS1细菌不仅可以在蚊子种群之间通过繁殖传给下一代,同时还可以通过交配活动从携带细菌的成蚊传到未携带细菌的成蚊中.因此为了更加全面地分析共生工程细菌Serratia AS1细菌在蚊子中的传播,我们建立了Serratia AS1细菌下蚊子具有阶段结构的数学模型.
全文HTML
-
首先,令l1,x,l2,y分别表示野生幼蚊、野生成蚊、携带细菌幼蚊、携带细菌成蚊的数量.随后,记
$\frac{{{a_1}{x^2}}}{{x + y}}$ 为野生成蚊和野生成蚊交配产生的后代的出生函数,其中a1表示野生成蚊与野生成蚊交配后野生幼蚊的出生率.记$\frac{{{a_2}{y^2}}}{{x + y}}$ 为携带细菌成蚊和携带细菌成蚊交配后携带细菌幼蚊的出生函数,其中a2表示携带细菌成蚊与携带细菌成蚊交配产生后代为携带细菌幼蚊的出生率.记$\frac{{{p_1}{a_3}xy}}{{x + y}}$ 为野生成蚊和携带细菌成蚊交配后产生的后代中一部分为未带菌幼蚊和一部分为携带细菌幼蚊的出生函数,其中a3表示野生成蚊和携带细菌成蚊进行交配产生后代的出生率,p1表示产生的后代中野生幼蚊所占的比值.接下来考虑Serratia AS1细菌在蚊子种群中的水平传播.令c为野生的成年蚊子与携带细菌的成年蚊子的性接触率,γ为携带细菌成蚊与野生成蚊交配后野生成蚊变为携带细菌成蚊的概率,得到细菌在蚊子种群中的水平传播函数为$\frac{{rcxy}}{{x + y}}$ .最后,考虑蚊子种群的特点,规定几个常用参数.记δ为幼蚊的成熟率,μ1为幼蚊的死亡率,则μ2为成蚊的死亡率,α为幼年蚊子种群之间进行竞争的概率.至此,我们得到了系统(1).本系统的
$\frac{{rcxy}}{{x + y}}$ 和$\frac{{{p_1}{a_3}xy}}{{x + y}}$ 等传播项体现了细菌在蚊子之间的水平传播和成蚊之间的垂直传播,因而更加全面地反映了工程细菌在蚊子种群中的传播方式.
-
我们首先分析下列两个系统:
易求得系统(2)和系统(3)的正平衡点分别为
$\mathit{\boldsymbol{E}}_1^c = (l_1^{(0)}, {x^{(0)}}), \mathit{\boldsymbol{E}}_2^c = (l_2^{(0)}, {y^{(0)}})$ ,其中引理1 当a1δ>μ1μ2+δμ2时,系统(2)仅存在正平衡点
$\mathit{\boldsymbol{E}}_1^c$ 且全局渐近稳定;当a2δ>μ1μ2+δμ2时,则系统(3)仅存在正平衡点$\mathit{\boldsymbol{E}}_2^c$ ,且全局渐近稳定.证 首先,计算系统(2)在
$\mathit{\boldsymbol{E}}_1^c$ 的雅可比矩阵为经计算,当δa1>μ1μ2+δμ2时,DetJ1>0,TrJ1 < 0.因此J1的两个特征值含有负实部,则
$\mathit{\boldsymbol{E}}_1^c$ 局部渐近稳定.下面分析
$\mathit{\boldsymbol{E}}_1^c$ 的全局稳定性.构造函数${B_1}({l_1}, x) = \frac{1}{{\alpha {l_1} + 1}}$ 有将(4)式沿着系统(2)求导,得到
由Dulac定理[9]可知,系统(2)在平面内无极限环,则
$\mathit{\boldsymbol{E}}_1^c$ 全局渐近稳定.参考以上方法,$\mathit{\boldsymbol{E}}_2^c$ 全局渐近稳定.参考系统(2)和系统(3)正平衡点的分析,得到系统(1)的边界平衡点为
经分析,下面定理显然成立.
定理1 系统(1)的边界平衡点
$\mathit{\boldsymbol{E}}_i^{(0)}(i = 1, 2)$ 存在的充分必要条件为${a_i} > {\mu _2} + \frac{{{\mu _1}{\mu _2}}}{\delta }, i = 1, 2$ .下面分析边界点$\mathit{\boldsymbol{E}}_1^{(0)}$ 和$\mathit{\boldsymbol{E}}_2^{(0)}$ 的局部稳定性.定理2 当
$\gamma c < {\mu _2}\left[ {1 - \frac{{{a_3}(1 - {p_1})}}{{{a_1}}}} \right]$ 成立时,$\mathit{\boldsymbol{E}}_1^{(0)}$ 局部渐近稳定;当$\gamma c > {\mu _2}\left( {\frac{{{p_1}{a_3}}}{{{a_2}}} - 1} \right)$ 成立时,$\mathit{\boldsymbol{E}}_2^{(0)}$ 局部渐近稳定.证 首先,计算系统(1)在
$\mathit{\boldsymbol{E}}_1^{(0)}$ 的雅可比矩阵为其中
经计算,当
$\gamma c < {\mu _2}\left[ {1 - \frac{{{a_3}(1 - {p_1})}}{{{a_1}}}} \right]$ 时,DetJ3>0,TrJ3 < 0.因此J3的两个特征值含有负实部.结合引理1,当$\gamma c < {\mu _2}\left[ {1 - \frac{{{a_3}(1 - {p_1})}}{{{a_1}}}} \right]$ 时,系统(1)的边界平衡点$\mathit{\boldsymbol{E}}_1^{(0)}$ 局部渐近稳定.类似地,当$\gamma c > {\mu _2}\left( {\frac{{{p_1}{a_3}}}{{{a_2}}} - 1} \right)$ 时,系统(1)的边界平衡点$\mathit{\boldsymbol{E}}_2^{(0)}$ 局部渐近稳定.接下来研究系统(1)边界点的全局稳定性.限于技术原因,仅考虑γ=0,系统(1)简化为以下系统:
经分析得到下面定理.
定理3 当a1 < a3(1-p1)且a2>a3p1时,系统(5)的边界点平衡点
$\mathit{\boldsymbol{E}}_2^{(0)}$ 全局渐近稳定;当a2 < a3p1且a1>a3(1-p1)时,系统(5)的边界点平衡点$\mathit{\boldsymbol{E}}_1^{(0)}$ 全局渐近稳定.证 首先,利用文献[8]中的变量代换.令
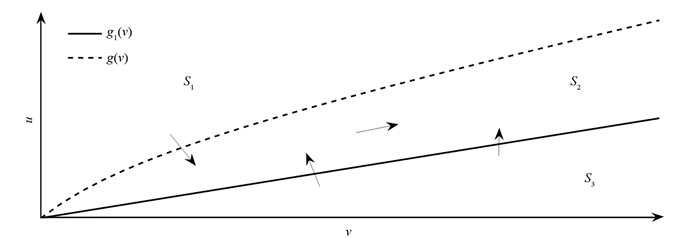
$ u = \frac{{{l_2}}}{{{l_1}}}, v = \frac{y}{x}$ ,得到下面系统:接下来分析由u和v张成的向量场平面图(图 1).令(6)式的第1,2方程的右端为零,得到下面两个函数:
根据g(v),g1(v),向量场可以分为3部分S1,S2和S3,其中
记
经计算,当a2>a3p1且a1 < a3(1-p1)时,g2(v)>0(v>0)恒成立.因此(v,u)∈S1时,(v,u)最终进入S2.当(v,u)∈S3时,(v,u)最终进入S2.当(v,u)∈S2时,S2为不变集.需保证
$\frac{{{\rm{d}}u}}{{{\rm{d}}t}} > 0, \frac{{{\rm{d}}v}}{{{\rm{d}}t}} > 0$ ,不妨设$(v, u) \to \mathit{\boldsymbol{K}} = ({k_1}, {k_2}), \mathit{\boldsymbol{K}} \in {S_2}$ ,此时$\frac{{{\rm{d}}u}}{{{\rm{d}}t}} + \frac{{{\rm{d}}v}}{{{\rm{d}}t}} > 0 = 0$ .另一方面由其中
${q_1} = \frac{{{a_2}{v^2} + {a_3}(1 - {p_1})v - {a_3}{p_1}uv - {a_1}u}}{{1 + v}}$ ,q2=u-v,二者矛盾.或者当ki(i=1,2)→+∞时$\frac{{{\rm{d}}v}}{{{\rm{d}}t}} \to 0$ ,$\frac{{{\rm{d}}u}}{{{\rm{d}}t}} \to + \infty \left( {\frac{{{\rm{d}}v}}{{{\rm{d}}t}} \to + \infty , \frac{{{\rm{d}}u}}{{{\rm{d}}t}} \to 0} \right)$ ,显然矛盾.因此u→+∞,v→+∞(t+∞).由于对∀M∈$\mathbb{R}$+,存在t0使得当t>t0时,有v(t)>M.因此
$\frac{{{\rm{d}}{l_1}}}{{{\rm{d}}t}} + \frac{{{\rm{d}}x}}{{{\rm{d}}t}} < - \left[ {{\mu _2} - \frac{{{a_1}}}{{1 + M}}} \right]x - {\mu _1}{l_1}$ .设μ2=μ1+ε,ε>0,则记
$\frac{{{\rm{d}}{l_1}^*}}{{{\rm{d}}t}} + \frac{{{\rm{d}}{x^*}}}{{{\rm{d}}t}} = - {\mu _1}({l_1}^* + {x^*})$ ,取初始值为(l10,x0),有(l1*+x*)→0(t>t0).根据比较定理有(l1+x)→0(t→+∞),因此l1→0,x→0(t→+∞).易证l2,y有界,结合引理1可知(l2,y)→(l2(0),y(0))(t→+∞).因此$\mathit{\boldsymbol{E}}_2^{(0)}$ 全局吸引.类似地,令$u = \frac{{{l_2}}}{{{l_1}}}, v = \frac{y}{x}$ ,则$\mathit{\boldsymbol{E}}_1^{(0)}$ 全局吸引得证. -
直接对系统(1)的地方病平衡点进行分析是困难的.同样地,利用文献[8]中的变量代换.令
$u = \frac{{{l_2}}}{{{l_1}}}, v = \frac{y}{x}$ ,得到系统(7):下面分析系统(7)的正平衡点.令系统(7)的第2,4方程的右端为零,计算得到
将(8)式代入(7)式的第1方程中,并且令该方程为零,得到
其中A1=b1+a2γc,A2=b1+b2+a3γc,A3=b2+a1γc,记b1=(a2-a3p1)μ2,b2=[a3(1-p1)-a1]μ2.另外,记函数F(v)的判别式为Δ.则对于系统(1)正平衡点存在性的讨论,即为对系统(7)的正解讨论,从而将其转化为对二次函数F(v)的正解讨论,因此得到下面定理.
定理4 (i)当Δ < 0时,则系统(1)没有地方病平衡点.
(ii) 当Δ>0且A1A3>0,A1A2>0成立时,系统(1)没有地方病平衡点.
(iii) 当Δ=0且A1A3>0,A1A2 < 0成立时,系统(1)有且仅有一个地方病平衡点E1.
(iv) 当Δ>0且A1A3 < 0,A1A2>0成立时,系统(1)有且仅有一个地方病平衡点E1.
(v) 当Δ>0且A1A3>0,A1A2 < 0成立时,系统(1)有两个地方病平衡点E1和E2.
接下来,我们仅考虑两种特定参数下的两个系统.令a1=a2,p1=0,得到下面系统:
经过分析该系统的地方病平衡点得到下面定理.
定理5 当
$\gamma c < {\mu _2}\left( {1 - \frac{{{a_3}}}{{{a_1}}}} \right)$ 时,系统(9)有且仅有一个地方病平衡点E1,且E1是一个鞍点.证 类似系统(7)正解存在的讨论方法,只讨论二次函数F1(v)的正解即可.经计算
由于Δ>0,且函数F1(v)的对称轴小于零,则当
$\gamma c < {\mu _2}\left( {1 - \frac{{{a_3}}}{{{a_1}}}} \right)$ 时系统(9)有且仅有一个正平衡点.令v1为F1(v)的一个正解,令系统(9)的第3,4方程右端为零,计算得到显然l11>0,则x1>0.根据
$u = \frac{{{l_2}}}{{{l_1}}}, v = \frac{y}{x}$ 可知l21>0,y1>0.因此系统(9)存在一个地方病平衡点.接下来,分析系统(9)正解的稳定性.记系统(9)的正解为E1=(u1,v1,l11,x1).计算系统(9)在E1的雅可比矩阵为
随后,可得系统(9)在E1的特征多项式中的常数项h0.记h0=h1+h2,其中
由于
$\gamma c < {\mu _2}\left( {1 - \frac{{{a_3}}}{{{a_1}}}} \right)$ ,且a3 < a1,所以h1 < 0,h2 < 0,即h0 < 0.故系统(9)有且仅有一个地方病平衡点E1,且E1是一个鞍点.接下来,令a1=a2,p1=1 2,α=1,我们得到下面模型:
参考定理5的证明得到下面定理.
定理6 当
$\left[ {{a_1}\gamma c + \left( {\frac{{{a_3}}}{2} - {a_1}} \right){\mu _2}} \right]\left[ {{a_1}\gamma c + \left( {{a_1} - \frac{{{a_3}}}{2}} \right){\mu _2}} \right] < 0$ 时,则系统(10)有且仅有一个地方病平衡点E1.
2.1. 边界平衡点
2.2. 正平衡点的存在性
-
本文根据Serratia AS1细菌在蚊子种群中的传播特点,建立了蚊子种群动力学模型.我们得到系统边界平衡点的局部稳定性和正平衡点的存在性.随后,我们得到仅在垂直传播下,若参数满足a1 < a3(1-p1)和a2>a3p1条件,最终仅有携带细菌的蚊子存活;若参数满足a1>a3(1-p1)和a2 < a3p1条件,最终仅有野生蚊子存活.最后在特定参数下得到若参数满足
$\gamma c < {\mu _2}\left( {1 - \frac{{{a_3}}}{{{a_1}}}} \right)$ ,则野生蚊子和携带细菌的蚊子共存.综合以上分析,若最终仅有携带细菌蚊子存活,可以有效抑制疟原虫的生长,即可以有效抑制疟疾的传播.



 下载:
下载: