-
开放科学(资源服务)标志码(OSID):

-
拉索的振动具有强烈的几何非线性特点,长时间的振动可能导致桥梁断裂、拱结构倒塌,进而造成人员伤亡、危害国民经济[1-3]. 拉索的非线性动力学研究,起源于16世纪,成形于18世纪中期[2]. 同时,拉索也是应用力学学科研究的基本元素,是分析各种动力学现象的经典模型,在土木工程中,拉索可能存在面内振动和面外摆动的耦合内共振现象[4],也可能存在拉索—梁组合模型之间相互耦合共振的现象[5],还可能存在拉索—拱组合模型之间相互耦合共振的现象[6].
20世纪末期,Irvine系统地研究拉索的模态、频率,给出了拉索各模态之间可能发生耦合共振的条件并提出了重要的Irvine系数,该参数是与拉索几何参数有关的重要参数,对拉索动力学特征分析起着尤为重要的作用[7]. 1992年,Perkins等利用一阶摄动分析方法,研究了由参数激励和强迫激励引起的拉索面内和面外周期运动的存在性和稳定性,分析了稳定分岔条件. 结果表明,当拉索面内的自振频率与面外的自振频率之间满足2∶1关系时,面内的稳定性会降低,面外的稳定性会增强[8]. 2009年,Wang等利用多尺度法研究了具有多个内共振的拉索的非线性响应,得到拉索的平均方程和近似解. 利用频率—响应曲线和激励—响应曲线分析了平均方程及其稳定性,还分析了激励幅值对拉索的频率—响应曲线的影响[9]. 2018年,Zhao等研究了双频激励下温度对悬索非线性振动特性的影响,研究发现,温度变化对软化或硬化型弹簧的性能、响应幅值、共振范围、分支交叉和分支数目、稳态解的数目和相位都有影响[10-11].
针对拉索的非线性振动特征分析,许多文献都忽略了弯曲刚度的影响. 实际工程中,拉索的弯曲刚度随着其直径的增大而增大,且弯曲刚度会影响拉索的自振频率,进而可能导致拉索的振动性质发生改变,因此,研究特大直径斜拉索的振动特征时忽略弯曲刚度可能并不合理. 为此,吴庆雄等推导了考虑弯曲刚度影响的拉索面内、面外耦合振动的理论公式,接着采用有限差分法验证了该公式的正确性[12]. 赵跃宇等研究了弯曲刚度对拉索面内、面外的1阶固有频率及高阶固有频率的影响,研究结果表明,弯曲刚度对面外固有频率的影响大于面内,弯曲刚度对固有频率的影响随着模态函数阶次的增加而增大[13]. 吕建根等在文献[13]的基础上进一步研究了弯曲刚度对拉索面内、面外内共振的影响,获得了有意义的结论[14].
本文将桥面简化为一个质量块,建立了索桥耦合动力学模型,将该耦合动力学模型分解为一个强迫振动模型与一个参数振动模型,针对参数振动模型进行了系统的动力学分析,研究了拉索面内、面外的耦合内共振,且进一步分析了弯曲刚度对拉索振动特征的影响,得出了一些有价值的结论,能给实际工程提供一些理论指导.
全文HTML
-
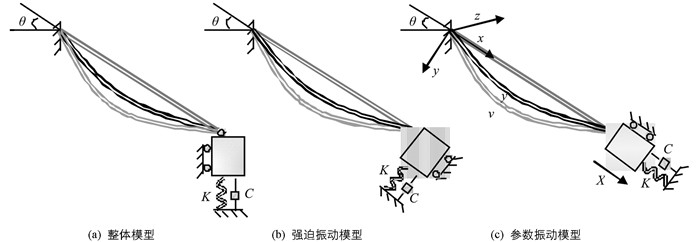
首先建立索桥耦合振动模型,如图 1所示,图 1(a)为整体模型,其可分离为一个强迫振动模型图 1(b)与一个参数振动模型图 1(c),本文的研究对象仅针对图 1(c),即只分析索桥耦合系统的参数振动. 本文只考虑拉索的抗弯刚度,忽略了扭转刚度与剪切刚度对拉索振动特征的影响,且认为拉索在重力作用下的静态平衡构型为抛物线. 为便于推导拉索面内、面外的耦合非线性振动方程,首先建立笛卡尔坐标系,拉索的跨径方向设为x轴,y轴正方向垂直于x轴向下,z轴正方向垂直于重力平面向内.
图 1中v表示拉索的y轴方向的动态位移,X表示桥面的滑动位移,K为桥面的刚度,C为桥面的阻尼,θ为斜拉索的倾角,且本文用u表示拉索x轴方向的动态位移,w表示拉索z轴方向的动态位移.
由哈密顿变分原理可得
式(1)中δkv为拉索的动能,δ∏为拉索的势能,δw′为拉索所受非保守力做功.
根据式(1)可得
式(3)中H表示拉索的初始张力,EI为拉索的弯曲刚度,m为拉索的单位质量,τ为拉索的动张力,且其表达式为
式(4)中EA为拉索的拉伸刚度.
在本文建立的参数振动模型下,动张力τ不仅与拉索的初始垂度等几何非线性因数有关,还与桥面的滑动位移有关. 考虑桥面的滑动位移,且忽略拉索轴向的位移,式(4)可转变为
式(5)中l为拉索的跨径.
将式(5)代入式(2)中可得
拉索的振动特征主要受其一阶模态的影响,因此根据一阶模态叠加法可将动态位移v和w分别表示为
式(8)和式(9)中,φ1,φ2表示振型函数,q1,q2表示振动函数.
将式(8)和式(9)代入式(7)且使用Galerkin法可得
式(7)中“·”为时间t的一阶导数,其他系数表达式为
根据牛顿第二定律可得桥面的振动方程为
将式(8)和式(9)代入式(12)可得
式(13)中的系数表达式为
联立式(10)和式(11)与式(13)且考虑拉索的黏性阻尼可得斜拉索—桥耦合参数振动方程组,即
式(14)中“··”为时间t的二阶导数,
${\tilde \eta _9} = \int\limits_0^l {{\xi _v}} \varphi _2^2{\rm{d}}x, {\rm{ }}{\tilde \vartheta _7} = \int\limits_0^l {{\xi _w}} \varphi _2^2{\rm{d}}x, {\xi _v}$ 和ξw分别为y轴和z轴方向的黏性阻尼系数.
-
近几十年来,随着学者们的不断努力,非线性振动领域蓬勃发展,进一步完善了多种非线性定量分析方法,例如多尺度法、平均法、渐进法等. 多尺度法具有较高的精度,且非常适用于弱非线性系统的振动特征分析,因此本文亦选择多尺度法[13-17]. 为方便多尺度法的运用,需对公式(14)进行处理,即将式(14)转变为
式(15)中ε为无量纲的小参数,其他系数表达式分别为
将式(15)的解设为
式(16)中T0=t,物理意义为时间t的快变化;T1=εt,物理意义为时间t的慢变化. x11,x21,x31为派生系统的周期解,x12,x22,x32为派生系统的修正解.
将式(16)代入式(15)并整理小参数ε的同次幂得到ε0次项
ε1次项
式(17)与式(18)中,
${D_0} = \frac{\partial }{{\partial {T_0}}}, {D_1} = \frac{\partial }{{\partial {T_1}}}$ .将式(17)的解设为
式(19)中的cc为共轭项,A1,A2,A3为派生系统的振幅,i为虚数单位.
将式(19)代入式(18)中可得
观察式(20)可知索桥耦合系统存在ω3≈ω1≈ω2(1∶1∶1)这种共振模式,下面将基于龙格—库塔(Runge-Kutta)方法来分析该系统的1∶1∶1共振.
-
龙格—库塔方法的精度高,因此被广泛地运用于工程中,由于此算法采取了较好的措施对误差进行抑制,所以其计算原理也较复杂,下面将简单介绍其计算原理.
针对一阶精度的欧拉公式有
式(21)中h表示计算步长,且yi+1的表达式完全等价于y(xi+1)的Taylor展开式的前两项,即局部截断误差为O(h2).
用点xi处的斜率k1与点xi+1处的斜率k2的加权平均值作为平均斜率k*的近似值,那么就会得到二阶精度的改进欧拉公式:
依次类推,如果在区间[xi,xi+1]内多预估几个点的斜率k1,k2,…,km,并用它们的加权平均数作为平均斜率k*的近似值,且增加计算次数,可以提高截断误差的阶,它们的误差估计可以用f(xi,yi)在xi处的Taylor展开来表示. 于是可考虑用函数f(xi,yi)在若干点上的函数值的线性组合来构造瑞利—金斯公式,构造时要求近似公式在f(xi,yi)处的Taylor展开式与解y(x)在xi处的Taylor展开式的前面几项重合,从而使瑞利—金斯公式达到所需要的阶数. 换而言之,在[xi,xi+1]这一步内计算多个点的斜率值,然后将其进行加权平均,再作为平均斜率k*的近似值,即可构造出更高精度的计算公式,这就是龙格—库塔方法的原理.
一般的龙格—库塔方法形式为
式(23)即为p阶龙格—库塔方法,其中ai,bij,ci为待定系数
当然,学术界常用的是四阶龙格—库塔方法,也就是在[xi,xi+1]上用4个点的斜率加权平均作为平均斜率k*的近似值,构成一系列四阶龙格—库塔计算公式.
令式(23)中p=4,可得四阶龙格—库塔方法的计算形式为
当选择一定的初始扰动条件,就能基于四阶龙格—库塔计算原理,通过MATLAB编程脚本程序求得索桥耦合系统的位移响应.
-
如果拉索的弹性模量E=2.0×1011 Pa,单位质量m=30 kg/m,跨径l=120 m,截面惯性矩I=1.75×10-5 m4,截面面积A=0.015 m2,拉索的张力H=2×106 N,桥面的等效质量M=6.5×105 kg,等效刚度K=5×106 N/m,此时的物理参数刚好使得ω3≈ω1≈ω2,为方便区分,设此时的1∶1∶1共振模式为模式1. 如果拉索的弹性模量E=2.0×1011 Pa,单位质量m=30 kg/m,跨径l=350 m,截面惯性矩I=1.75×10-5m4,截面面积A=0.015 m2,拉索的张力H=4×106 N,桥面的等效质量M=13×105 kg,等效刚度K=5×106 N/m,此时的物理参数也刚好使得ω3≈ω1≈ω2,为方便区分,设此时的1∶1∶1共振模式为模式2. 选择上面这两套物理参数都刚好使得ω3≈ω1≈ω2,即索桥耦合系统之间存在1∶1∶1共振模式.
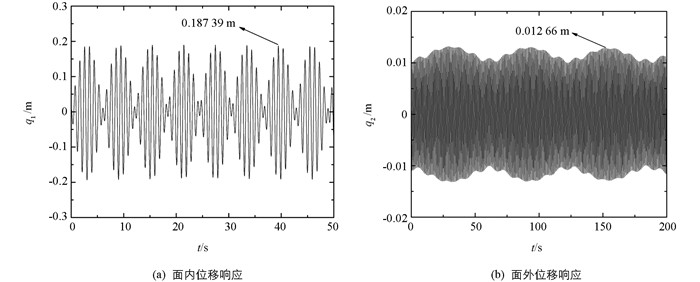
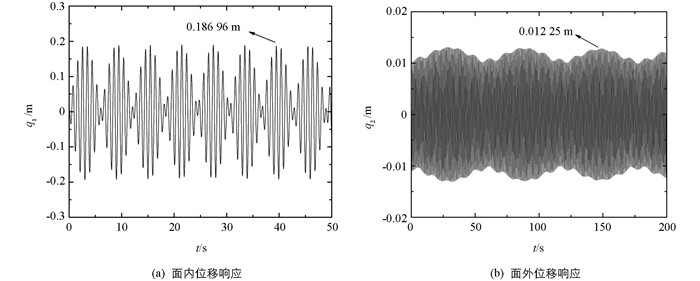
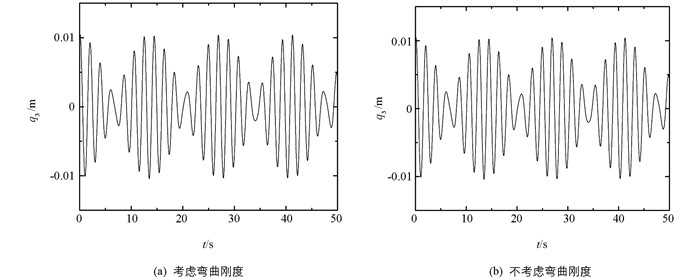
初始扰动条件为[0.01,0.01,0.01,0.01,0.01,0.01 m],忽略该系统所受阻尼,使用四阶龙格—库塔方法可得到模式1下拉索面内、面外、桥面的位移响应曲线,如图 2、图 3、图 4所示.
观察并对比图 2、图 3、图 4可得知:索桥耦合系统发生1∶1∶1共振时,拉索面内和面外都存在一定的位移,但面内的振动位移远大于面外的摆动位移;能量在拉索面内、面外以及桥面之间往复传递,且能量具有“拍”的特点;考虑弯曲刚度对拉索振动特征影响时,拉索面内的振幅为0.187 39 m,不考虑弯曲刚度对拉索振动特征影响时,拉索面内振幅为0.186 96 m,减少了0.000 43 m;考虑弯曲刚度对拉索振动特征影响时,拉索面外的振幅为0.012 66 m,不考虑弯曲刚度对拉索振动特征影响时,拉索面外振幅为0.012 25 m,减少了0.000 41 m;弯曲刚度会使得振幅增加,但由于本文是考虑的小直径斜拉索,因此拉索面内、面外振幅值的增加较小,但是针对特大直径拉索振动特征分析时需考虑弯曲刚度引起的拉索振幅的变化.
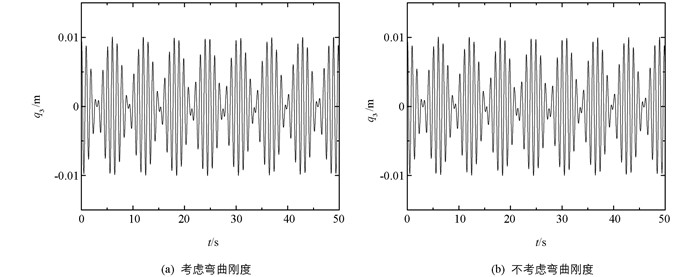
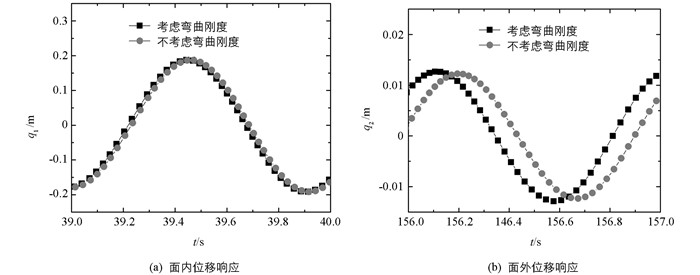
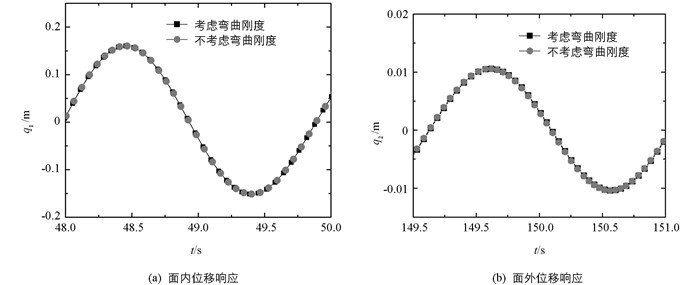
从图 2、图 3得知:对于小直径拉索,弯曲刚度对拉索振幅的影响较小,但从图 2、图 3中不能得知弯曲刚度对发生共振的条件的影响,为了更加清晰地分析弯曲刚度对拉索面内、面外发生共振的条件的影响,取图 2、图 3中的局部数据得到图 5.
观察图 5得知:弯曲刚度并没有改变拉索共振的性质,但拉索发生共振的条件却明显有向左偏移的趋势,且面内偏移的趋势不明显,但面外偏移的趋势很显著,即弯曲刚度对面外发生共振的条件有明显的影响.
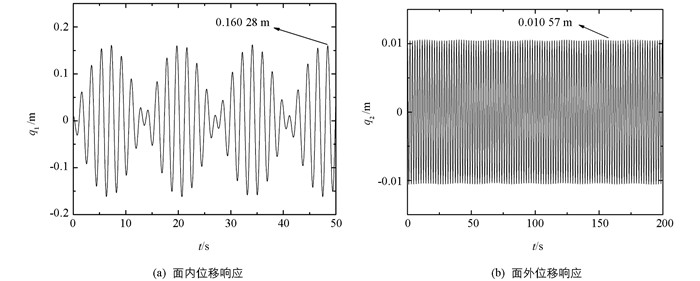
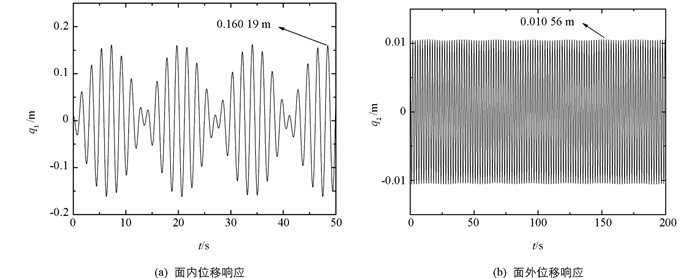
同理,使用四阶龙格—库塔方法可得到模式2下拉索面内、面外、桥面的位移响应曲线,如图 6、图 7、图 8所示.
观察并对比图 6、图 7、图 8可得知:与模式1相似,模式2下的拉索在面内和面外都存在一定的位移,但面内的振动位移远大于面外的摆动位移;能量在拉索面内、面外、桥面之间往复传递,且能量具有“拍”的特点;考虑弯曲刚度对拉索振动特征影响时,拉索面内的振幅为0.160 28 m,不考虑弯曲刚度对拉索振动特征影响时,拉索面内振幅为0.160 19 m,减少了0.000 09 m;考虑弯曲刚度对拉索振动特征影响时,拉索面外的振幅为0.010 57 m,不考虑弯曲刚度对拉索振动特征影响时,拉索面外振幅为0.010 56 m,减少了0.000 01 m;模式2下的弯曲刚度对振幅的影响相比模式1下弯曲刚度对振幅的影响小,这是因为随着档距与张力的增加涉及到弯曲刚度项的系数值会下降,即针对张力较大的大跨越拉索振动特性分析时,可忽略弯曲刚度对振幅的影响.
同理,与模式1类似,取图 6、图 7中的局部数据得到图 9. 从图 9可发现:弯曲刚度几乎没有使得模式2发生共振的条件左偏,这同样是因为大张力、大跨径拉索的振动方程中涉及到弯曲刚度项的系数值较小,即可忽略大张力、大跨径拉索的弯曲刚度对其共振发生的条件的影响.
-
本文建立了索桥耦合动力学模型,并推导了该模型的振动方程,通过多尺度法分析了该系统存在的共振模式,并介绍了四阶龙格—库塔方法的计算,最后通过算例分析得知:
1) 拉索面内、面外、桥面之间的耦合效应非常强烈,即能量在拉索面内、面外、桥面之间往复传递,能量形式具有“拍”的特点. 工程中应避免耦合效应的发生,从而提高结构的安全性.
2) 索桥耦合系统发生1∶1∶1共振时,拉索在面内和面外都存在一定的位移,但面内的振动位移远大于面外的摆动位移,因系统发生共振时,面外的位移也仅为百分之几,那么对于考虑多种因素影响(如桥台与拉索之间的相互作用、风雨激励、覆冰等)的索桥耦合系统的动力学建模,可忽略面外的摆动位移,从而提高效率.
3) 弯曲刚度对拉索面外振幅的影响更为显著,针对小直径拉索动力学分析时,可忽略弯曲刚度对拉索振动特征的影响,但针对特大直径拉索动力学分析时,需考虑弯曲刚度对拉索振动特征的影响.
4) 对于小跨径、小张力的拉索,弯曲刚度不会改变拉索共振的性质,但会使得拉索发生共振的条件具有向左偏移的趋势,且面内偏移的趋势不明显,但面外偏移的趋势很显著.
5) 对于大跨径、大张力的拉索,因涉及到弯曲刚度项的系数值随着档距与张力会下降,即针对张力较大的大跨越拉索振动特性分析时,可忽略弯曲刚度对拉索发生共振的条件的影响.



 下载:
下载: