下述定理表明了模型(1)的解的非负性和有界性.

定理1  ${\mathbb{R}}_ + ^2$是模型(1)的解的正不变集，且满足非负初始条件(即x(0)≥0，y(0)≥0)的解最终落入下列区域中.

其中

证  对于模型(1)，当x>0，y>0时，有x′|_x=0=by>0，y′|_y=0=gx>0. 因此${\mathbb{R}}_ + ^2$是模型(1)的解的正不变集.

进一步，由模型(1)的第一个方程得

其中，

因此

这意味着对于任意小的ε>0，存在T>0，使得当t>T时，有x < M+ε. 所以由模型(1)的第二个方程得

其中

进一步有$0 \le \mathop {\lim \sup }\limits_{t \to \infty } y\left( t \right) \le {N_\varepsilon }$. 由于ε是任意小的正数，于是有

因此，满足非负初始条件的解最终落入区域Ω={(x，y)|0≤x≤M，0≤y≤N}中，其中

为了求得模型(1)的平衡点，令模型(1)的右边为零，得到

方程组(2)的正解即为模型(1)的内平衡点. 显然，模型(1)总存在灭绝平衡点E₀=(0，0).

由方程组(2)的第一个方程可以得到

其中，在(0，M)内b-cx(1+αx)>0，当x≠0时，将(3)式代入方程组(2)的第二个方程有

记

根据模型(1)的正不变集Ω可知，G(x)=0在(0，M)内的零点对应模型(1)内平衡点的横坐标x. 可以通过判断方程G(x)=0在区间(0，M)内根的存在性确定模型(1)内平衡点的存在性.

对函数G(x)求导得到

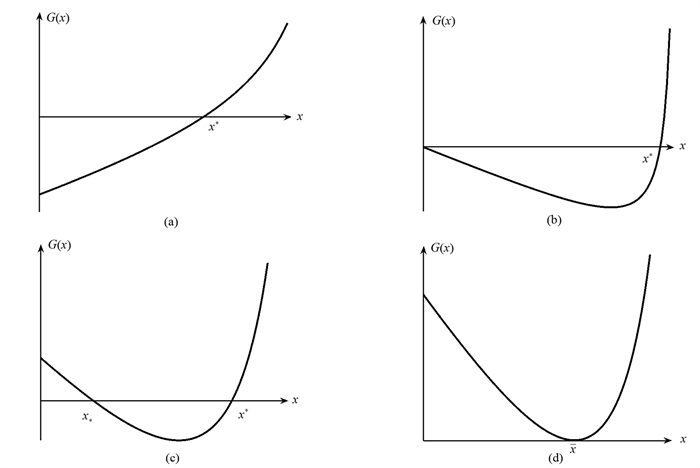
易知函数G(x)有以下性质：

于是关于方程G(x)=0正根的存在性有如下几种情形：

(i) 当g≥e(m+g)时，有G′(x)>0，当且仅当G(0) < 0时函数G(x)在区间(0，M)内有唯一零点，记为x^*.

(ii) 当g < e(m+g)时，由于$G'''$(x)>0，故若G″(0)>0时有G″(x)>0，即G(x)的图形是上凹的，若G″(0) < 0，则存在x₀使得G(x)在区间(0，x₀)内是凸的，在区间(x₀，M)内是凹的. 此时，如果G′(x)=0，则G(x)在区间(0，M)内有唯一的极小值点x其中x₀ < x故

① 若G(0) < 0或G(0)=0且G′(0) < 0，则函数G(x)在区间(0，M)内有唯一零点，记为x^*.

② 若G(0)>0，G′(0) < 0且G(x) < 0，则函数G(x)在区间(0，M)内有两个不同的零点，分别记为x_*和x^*，其中x_* < x < x^*.

③ 若G(0)>0，G′(0) < 0且G(x)=0，则函数G(x)在区间(0，M)内有一个二重零点，记为. 当G(0)=0时，

因此，关于模型(1)在正不变集Ω上平衡点的存在性有如下定理：

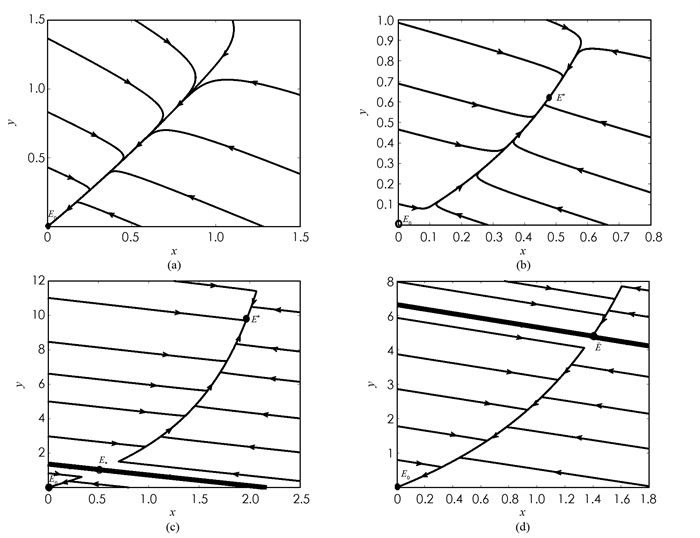
定理2  (i) 当满足下列条件之一时，模型(1)在区域Ω上有唯一的内平衡点E^*=(x^*，y^*)，

① μ(m+g) < bg(图 1(a));

② μ(m+g)=bg且gbk < μ(bec-μc-αbμ)(图 1(b)).

(ii) 当μ(m+g)>bg，$\frac{{k{{\left( {m + g} \right)}^2}}}{b}$+αμ(m+g)+c[g-e(m+g)] < 0且G(x) < 0时，模型(1)在区域Ω上有两个内平衡点E_*=(x_*，y_*)和E^*=(x^*，y^*)，其中x_* < x < x^*(图 1(c)).

(iii) 当μ(m+g)>bg，$\frac{{k{{\left( {m + g} \right)}^2}}}{b}$ +αμ(m+g)+c[g-e(m+g)] < 0且G(x)=0时，模型(1)在区域Ω上有唯一的内平衡点E =(x，y)(图 1(d)).

注：其中y_*，y^*和均由式子$y = \frac{{\left( {m + g} \right)\left( {1 + \alpha x} \right)x}}{{b - cx\left( {1 + \alpha x} \right)}}$和对应的x给出; 由于G′(0) < 0意味着g < e(m+g)，因此定理2中的(i)②，(ii)，(iii)未明确指出g < e(m+g).

关于模型(1)的平衡点的局部稳定性有如下结论：

定理3  (i) 对于模型(1)的灭绝平衡点E₀=(0，0)，当μ(m+g)>bg或μ(m+g)=bg且μ(bec-μc-αbμ)≤gbk时是渐近稳定的; 当μ(m+g) < bg或μ(m+g)=bg且μ(bec-μc-αbμ)>gbk时是不稳定的.

(ii) 对于内平衡点，E_*是不稳定的，E^*是渐近稳定的，E是鞍结点.

证  (i) 模型(1)在E₀=(0，0)处的Jacobi矩阵为

则它的特征值分别为

易知，当μ(m+g)>bg时λ₁ < λ₂ < 0，故E₀=(0，0)是稳定的结点; 当μ(m+g) < bg时λ₁ < 0 < λ₂，故E₀=(0，0)是不稳定的鞍点; 当μ(m+g)=bg时λ₁ < 0=λ₂，故E₀=(0，0)是高阶奇点.

为了分析当μ(m+g)=bg时平衡点E₀=(0，0)的稳定性，将模型(1)在原点处线性化得

做以下变换

则模型(5)变为

其中

系统(6)的线性部分满足局部中心流形存在的条件^[12]，故设系统(6)在原点处的局部中心流形为v=h(u)=au²+o(u³)，两边关于t求导得$\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \left[ {2au + o\left( {{u^2}} \right)} \right]\frac{{{\rm{d}}u}}{{{\rm{d}}t}}$，结合系统(6)可得

将v=h(u)=au²+o(u³)代入(7)式，并比较左右两边u的同次幂系数可得

即

将(8)式代入系统(6)的第一个方程，得到中心流形上的解满足

若μ(bec-μc-αbμ)-gbk≠0，则E₀=(0，0)为鞍结点. 若μ(bec-μc-αbμ) < gbk，则在u>0一侧E₀=(0，0)是渐近稳定的; 若μ(bec-μc-αbμ)>gbk，则在u>0一侧E₀=(0，0)为鞍点，是不稳定的.

若μ(bec-μc-αbμ)=gbk，则

因此，当μ(bec-μc-αbμ)=gbk时，E₀=(0，0)是渐近稳定的. 综上所述，当μ(m+g)>bg或μ(m+g)=bg且μ(bec-μc-αbμ)≤gbk时，E₀=(0，0)是渐近稳定的; 当μ(m+g) < bg或μ(m+g)=bg且μ(bec-μc-αbμ)>gbk时，E₀=(0，0)是不稳定的.

(ii) 下面讨论模型(1)的内平衡点的稳定性.

模型(1)在任一内平衡点E处的Jacobi矩阵为

由方程组(2)的第一个方程可知

由方程组(2)的第二个方程可知

故

从而

将(3)式代入(10)式可得

对于内平衡点E^*=(x^*，y^*)，有G′(x^*)>0，即det(J (E^*))>0，因此E^*是渐近稳定的; 对于内平衡点E_*=(x_*，y_*)，有G′(x_*) < 0，即det(J (E_*)) < 0，因此E_*是不稳定的; 对于内平衡点E =(x，y)，有G′(x)=0，即det(J (E))=0，此时E_*和E^*重合为一个平衡点E，它是一个鞍结点.

在这一节，讨论平衡点的全局稳定性.

定理4  系统(1)没有闭轨.

证  令

取Dulac函数B(x，y)= $\frac{1}{{xy}}$，则

向量域〈BP，BQ〉的梯度为

当x>0，y>0时，$\nabla $·〈BP，BQ〉严格小于零. 由Dulac判别法知，不存在完全含于xy平面第一象限的闭轨.

定理5  对于模型(1)，

(i) 若只存在灭绝平衡点E₀=(0，0)，则一定是全局渐近稳定的.

(ii) 若μ(m+g) < bg，则内平衡点E^*=(x^*，y^*)是全局渐近稳定的.

证  (i) 若只存在灭绝平衡点E₀=(0，0)，则一定有μ(m+g)>bg，此时E₀=(0，0)是渐近稳定的，又因为系统(1)没有闭轨，根据Poincaré-Bendixson定理知，第一象限的任一轨道都收敛至灭绝平衡点E₀=(0，0).

(ii) 当μ(m+g) < bg时，系统(1)存在灭绝平衡点E₀=(0，0)和内平衡点E^*=(x^*，y^*)，其中E₀=(0，0)是不稳定的，E^*=(x^*，y^*)是渐近稳定的，又因为系统(1)没有闭轨，根据Poincaré-Bendixson定理知，第一象限的任一轨道都收敛至稳定的内平衡点E^*=(x^*，y^*).

以下对本文建立的模型进行数值模拟，以此来验证以上分析的正确性.

1) 取参数为b=0.58，α=0.01，m=0.3，μ=0.3，g=0.3，c=0.1，e=0.5，k=0.05，此时μ(m+g)>bg，模型(1)的灭绝平衡点E₀=(0，0)在Ω上是全局渐近稳定的(图 2(a)).

2) 取参数为b=0.8，α=0.01，m=0.3，μ=0.3，g=0.3，c=0.7，e=0.3，k=0.05，此时μ(m+g) < bg，模型(1)在Ω上存在唯一的内平衡点E^*=(0.478 43，0.622 3)，该平衡点E^*=(0.478 43，0.622 3)是全局渐近稳定的(图 2(b)).

3) 取参数为b=0.48，α=0.03，m=0.3，μ=0.3，g=0.483，c=0.15，e=0.752 3，k=0.002，此时，x=1.419 6，且μ(m+g)>bg，$\frac{{k{{\left( {m + g} \right)}^2}}}{b}$ +αμ(m+g)+c[g-e(m+g)] < 0，G(x) < 0，模型(1)在Ω上存在两个内平衡点E_*=(0.513 5，1.016 1)，E^*=(1.971 8，9.807 3). 其中，灭绝平衡点E₀是局部渐近稳定的，内平衡点E_*是不稳定鞍点，E^*是局部渐近稳定的. 此时种群发展的最终状态取决于模型(1)的初始条件，初始值位于E_*稳定流形下方的解将会收敛至灭绝平衡点E₀，初始值位于E_*稳定流形上方的解将会收敛至内平衡点E^*，初始值在E_*稳定流形上的解将会收敛至内平衡点E_*. 因此双稳定现象发生(图 2(c)中粗线代表它的稳定流形).

4) 取参数为b=0.475 86，α=0.03，m=0.3，μ=0.301 122 16，g=0.483，c=0.149，e=0.752 3，k=0.002，此时，x=1.399，且μ(m+g)>bg，$\frac{{k{{\left( {m + g} \right)}^2}}}{b}$ +αμ(m+g)+c[g-e(m+g)] < 0，G(x)=0，模型(1)在Ω上存在唯一内平衡点E =(1.399，4.412 7). 其中，灭绝平衡点E₀是局部渐近稳定的，内平衡点E是鞍结点. 此时种群发展的最终状态取决于模型(1)的初始条件，初始值位于E稳定流形下方的解将会收敛至灭绝平衡点E₀，初始值位于E稳定流形上方或在稳定流形上的解将会收敛至内平衡点E. 因此双稳定现象发生(图 2(d)中粗线代表它的稳定流形).

本文讨论了一个由常微分方程系统给出的幼年-成年两阶段结构模型，描述了其同类相食的动力学行为. 分析了模型平衡点的存在性和稳定性，通过Dulac定理排除了模型周期解的存在性，从而得到了模型的全局动力学行为. 通过对相应结果进行数值模拟发现在一定条件下系统会出现双稳定现象. 值得思考的是，该模型忽略了环境中的资源与同类相食行为之间的相互作用. 为了了解这二者的相互作用如何影响种群的长期动力学行为，下一阶段将对模型(1)做一些改进，考虑把资源作为状态变量或重要参数，使其更具有现实意义.