本文考虑以下状态方程：

性能指标为

其中：T>0，A∈${\mathbb{R}}$^n×n，B∈${\mathbb{R}}$^n×m，Q∈${\mathbb{R}}$^n×n，R∈${\mathbb{R}}$^m×m.

经典的LQ问题为：对于受控系统(1)，在平方可积的控制函数空间中，寻找最优控制，极小化二次性能指标J(·). 但在实际问题中，控制函数通常带有一定的约束. 本文中考虑使得系统状态达到特定目标的控制集，即状态带有终端约束的LQ问题. 对于状态的预期目标x_T∈${\mathbb{R}}$ⁿ，定义控制函数类

带终端约束的LQ问题(简记为CLQ问题)描述如下：

对于给定的x₀，x_T∈${\mathbb{R}}$ⁿ，寻找控制u^*(·)∈U，使得

如果满足(2)式的u^*(·)存在，则其被称为CLQ问题的最优控制，相应的状态x^*(·): = x(·；x₀，u^*(·))被称为最优状态，(x^*(·)，u^*(·))被称为最优对. 上述问题称为带有终端约束的线性二次最优控制问题(简称为CLQ问题).

为了保证控制集U的非空性和CLQ问题的可解性，我们在本工作中作如下假设：

(A) 系统(1)在区间[0，T]上精确能控，即Rank(B，AB，…，A^n-1B)=n；Q为半正定矩阵，R为正定矩阵.

引理1   系统(1)在[0，T]上精确能控的充要条件为系统(1)的Gram矩阵Ψ(0，T)可逆，其中

Φ(·)满足

采用拉格朗日乘子法，我们首先将CLQ问题转化为无约束的LQ问题. 引入拉格朗日泛函：

其中x(T)：=x(T；x₀，u(·))为系统(1)的状态在t=T处的值. 对于给定的λ，无约束的LQ问题即(LQ)_λ问题为：

对于给定的λ，x₀∈${\mathbb{R}}$ⁿ，寻找u^*_λ(·)∈L²(0，T；${\mathbb{R}}$^m)使得

如果对于某些参数λ∈${\mathbb{R}}$ⁿ，(LQ)_λ问题的最优控制u_λ^*(·)对应的系统(1)的状态满足条件

那么我们可以证明u_λ^*(·)也是CLQ问题的最优控制.

引理2   若(x_λ^*(·)，u_λ^*(·))为(LQ)_λ问题的最优对，且满足x_λ^*(T)=x_T，则(x_λ^*(·)，u_λ^*(·))也是CLQ问题的最优对.

证    因为u_λ^*(·)为(LQ)_λ问题的最优控制，所以对任意的u(·)∈L²(0，T；${\mathbb{R}}$^m)，满足x(T；x₀，u(·))=x_T，有

由此可得J(u_λ^*(·))≤J(u(·))，即u_λ^*(·)为CLQ问题的最优控制. 证毕.

利用引理2，求解CLQ问题的最优控制，就可以转化为求解如下两个子问题：

(1) (LQ)_λ问题的最优控制问题；

(2) 选择特定的参数λ*∈ ${\mathbb{R}}$n，使得(LQ)λ*问题的最优状态满足xλ**(T): = x(T；x0，u(·))=xT.

对于(LQ)_λ问题的可解性，有如下定理.

定理1    基于假设(A)，对任意的λ∈${\mathbb{R}}$ⁿ，(LQ)_λ问题唯一可解，并且u_λ^*(·)是(LQ)_λ问题的最优控制当且仅当(x_λ^*(·)，y_λ^*(·))满足如下耦合的正倒向方程：

证   (LQ)_λ问题唯一可解性可以用文献[1]第七章定理2.1的方法得到. 现在证明定理的剩余部分.

(必要性)若u_λ^*(·)是(LQ)_λ问题的最优控制，那么对任意的ε∈${\mathbb{R}}$，性能指标满足：

我们记

由系统(1)的线性特征，可得x_ε(·)=x_λ^*(·)+εx⁰(·). 这样

由ε的任意性，可得

另一方面，由方程组(4)容易得到

两边积分，从而

由(5)式和(6)式可得

又由u(·)的任意性，得到

(充分性) 若(x_λ^*(·)，y_λ^*(·))满足方程组(4)，那么对任意的u(·)∈L²(0，T；${\mathbb{R}}$^m)，

结合(6)式，可知(5)式成立. 展开J_λ(u_λ^*(·)+εu(·))并利用(5)式，可推出

因此，u_λ^*(·)是(LQ)_λ问题的最优控制. 证毕.

定理1给出了最优控制的开环表示，而在应用中，人们更希望给出闭环表示，即状态反馈形式. 接下来，我们就研究CLQ问题的闭环表示. 我们引入Riccati方程：

和两个常微分方程(简称ODE)：

关于方程(7)，(8)，(9)的适定性，读者可以参考文献[1, 5].

引理3   方程(7)存在唯一的解P(·)∈C([0，T]；S₊ⁿ)；方程(8)，(9)分别存在唯一的解φ(·)，y_λ(·)∈C([0，T]；${\mathbb{R}}$ⁿ)，其中S₊ⁿ表示n阶的半正定矩阵集.

定理2   对任意的λ∈${\mathbb{R}}$ⁿ，(LQ)_λ问题的唯一最优对(x_λ^*(·)，u_λ^*(·))有如下表示

其中φ(·)，y_λ(·)分别是方程(8)，(9)的解.

证    设x(·)是如下ODE的解

其中u_λ^*(·)=R^-1B^Ty_λ(·). 由定理1知，只需要方程(9)的解也满足方程

即可得u_λ^*(·)是(LQ)_λ问题的最优控制. 为证方程(9)的解也满足方程(11)，构造

利用方程(7)-(9)，我们可以得到

且$\hat {\boldsymbol{x}}$(0)=P(0)y_λ(0)+φ(0)=O_ny_λ(0)+x₀=x₀. 所以$\hat {\boldsymbol{x}}$(·)为方程(10)的解，由方程(10)解的唯一性知x(·)=$\hat {\boldsymbol{x}}$(·)=P(·)y_λ(·)+φ(·). 再次由方程解的唯一性得y_λ(·)=y(·)，因此结论成立. 证毕.

下面引入辅助系统

其中：$\hat {\boldsymbol{A}}$(·)=A-P(·)Q，$\hat {\boldsymbol{B}}$(·)=(${\boldsymbol{BR}}^{-\frac{1}{2}}$，P(·)${\boldsymbol{Q}}^{\frac{1}{2}}$).

引理4   系统(12)在[0，T]上精确能控的充要条件是系统(1)在[0，T]上精确能控.

证    设x(T；x₀，u(·))=x_T，令$\hat{\boldsymbol{u}}(\bullet)=\left(\begin{array}{l} \boldsymbol{R}^{\frac{1}{2}} \boldsymbol{u}(\bullet) \\ \boldsymbol{Q}^{\frac{1}{2}} \boldsymbol{x}(\bullet) \end{array}\right)$，则系统(12)表示为：

易知x(·)满足该方程，再由该方程解的唯一性，知$\hat {\boldsymbol{x}}$(·)=x(·)，从而$\hat {\boldsymbol{x}}$(T；x₀，$\hat {\boldsymbol{u}}$(·))=x_T，即得系统(12)精确能控等价于系统(1)精确能控. 证毕.

通过引入

则系统(12)的Gram矩阵为$\hat {\mathit{\pmb{Ψ}}}$(0，T)=$\int_0^T \hat {\mathit{\pmb{Φ}}}(s) \hat {\boldsymbol{B}}(s)\hat {\boldsymbol{B}^{{\rm{T}}}}(s) \hat {\mathit{\pmb{Φ}}}^{{\rm{T}}}(s)$ds. 由系统(1)能控性的假设和引理4，可知$\hat {\mathit{\pmb{Ψ}}}$ (0，T)可逆. 现在通过$\hat {\mathit{\pmb{Ψ}}}$(0，T)的可逆性来研究P(T)的可逆性.

引理5    P(T)是正定矩阵.

证   由P(·)，$\hat {\mathit{\pmb{Φ}}}$(·)满足的方程，直接计算知，

进一步对两边在[0，T]上积分，有

从而

由$\hat {\mathit{\pmb{Ψ}}}$(0，T)=$\int_{0}^{T} \hat{{\mathit{\pmb{Φ}}}}(s) \hat{\boldsymbol{B}}(s) \hat{\boldsymbol{B}}^{\mathrm{T}}(s) \hat{{\mathit{\pmb{Φ}}}}^{\mathrm{T}}(s) \mathrm{d} s$可知其半正定，且$\hat {\mathit{\pmb{Ψ}}}$ (0，T)可逆，故$\hat {\mathit{\pmb{Ψ}}}$ (0，T)正定. 最后，由$\hat {\mathit{\pmb{Ψ}}}$(0，T)正定以及$\hat {\mathit{\pmb{Ψ}}}$(T)可逆可得P(T)是正定矩阵. 证毕.

现在我们可以综合前面的结果，得到CLQ问题的可解性.

定理3   (LQ)_λ^*问题的最优控制u_λ^*(·)是CLQ问题的最优控制，其中λ^*=P^-1(T)(φ(T)-x_T).

证    由引理5知P(T)可逆，从而λ*存在. 由定理2知，对(LQ)λ*问题的最优状态xλ**(·)，有

最后由引理2知，u_λ^*(·)是CLQ问题的最优控制，即得结论. 证毕.

根据定理3，可以得到CLQ问题的基于状态反馈的最优对的计算方法. 具体计算步骤如下：

1) 选取最优参数λ^*.

① 解得Riccati方程(7)和ODE(8)的解P(·)，φ(·).

② 求解最优参数λ^*=P^-1(T)(φ(T)-x_T).

2) 解得最优参数λ^*所对应ODE(9)的解y_λ^*(·).

3) 求解最优对(xλ**(·)，uλ**(·))：

现在，我们通过一个具体的例子，利用上述计算方法，得到CLQ问题的最优对.

例1    考虑CLQ问题，其中T=1，x₀=0，A=1，B=1，x_T=1，Q=1，R= $\frac{1}{3}$.

解：将条件数据代入Riccati方程(7)得其精确解为

由ODE(8)解得

进而可以计算最优参数：

再由ODE(9)解得

最后可以计算最优对为

由例1可知，即便对于1维系统，要求解CLQ问题仍然十分复杂，这就促使我们研究上述计算方法的数值算法. 接下来我们上述的计算方法给出数值计算的版本，首先将时间区间[0，T]均分为N份，即有

其中t_i=$\frac{T}{N}$N =：iτ，i=0，1，…，N. 下面列出的是基于状态反馈的CLQ问题的数值算法.

CLQ问题数值算法：

1) 分解半正定矩阵为Q=Q₀^TΛQ₀，其中Q₀为n阶正交矩阵，

定义

2) 选取最优参数λ^*的近似值λ.

① 求解Riccati方程(7)如下：

采用Euler方法求解ODE(8)，得到其数值解φ_i，i=0，1，…，N.

② 求解近似最优参数λ

3) 利用Euler方法求解近似最优参数λ所对应ODE(9)，得到其数值解y_i，i=0，1，…，N.

4) 求解近似最优对(x_i，u_i)，i=0，1，…，N：

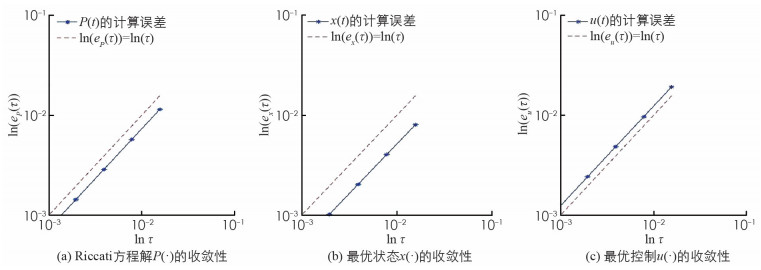
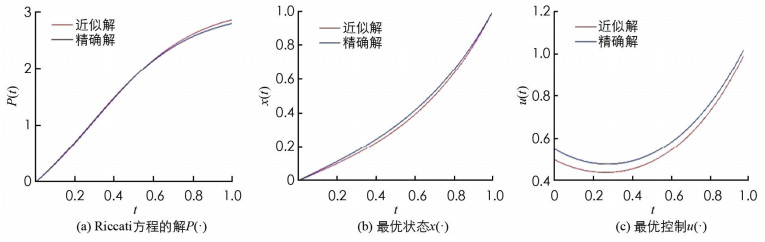
取N=2⁵，用数值算法得到例1的数值解，和精确解的比较见图 1.

为验证算法的收敛性，对于Riccati方程，定义其误差和步长的关系为：$e_{{\boldsymbol{P}}}(\tau)=\frac{1}{N+1} \sum\limits_{i=0}^{N}\left|\boldsymbol{P}_{i}-\boldsymbol{P}\left(t_{i}\right)\right|$，其中P(·)为Riccati方程的精确解，P_·为近似解. 类似地定义e_x(τ)，e_u(τ). 图 2展示了算法的收敛性，从图 2中可看出算法的收敛速度能够达到一阶.

本文利用参数选择的方法对带有终端约束的LQ问题给出了可解性的理论结果，同时基于最优控制的闭环表示给出了计算最优对的数值算法. 与基于开环表示的确定/随机系统的LQ问题算法相比，本文算法的优势在于：避免了条件数学期望的计算，避免使用梯度下降法等算法^[6-10]，从而大大减少了计算量.