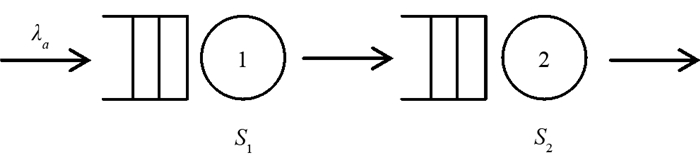
本文研究图 1所示的串联排队系统，该系统由两个站串联而成，每个站有一个服务器，并且服务器前的缓冲区无限大. 顾客的到达过程为更新过程，顾客到达系统后依次在每个站接受服务，服务完成后离开系统. 系统的服务规则为先到先服务(first come first served，FCFS)，每个服务器的服务时间服从一般分布.

假设系统的到达率为λ_a，相邻顾客到达时间间隔为X，X服从一般分布. 第1个站和第2个站的服务器的服务时间分别记为S₁和S₂. X，S₁和S₂的平方变异系数分别为C_a²，C_S1²和C_S2²，且

其中E(X)和D(X)分别表示到达时间间隔的期望和方差，E(S_i)和D(S_i)，i=1，2分别表示第1个站和第2个站的服务器的服务时间的期望和方差. 串联排队系统中第1个站和第2个站的服务强度分别记为ρ₁和ρ₂，且

令ρ=max{ρ₁，ρ₂}. 串联排队系统中第1个站和第2个站的平均排队时间分别记为W₁和W₂.

近年来，机器学习快速发展，广泛应用于数据挖掘、人工智能、医疗保健、排队等领域. 与传统回归方法相比，机器学习能够分析和挖掘数据中的规律，并对新的样本进行预测，适合处理复杂的回归问题. 下面介绍机器学习中常见的回归算法.

机器学习中常见的线性回归模型为多元线性回归(multiple linear regression，MLR)、岭回归(ridge regression，Ridge)以及套索回归(lasso regression，Lasso). 线性回归模型属于一种监督学习算法，研究两个随机变量之间的线性关系. 该模型可表示为

其中：X表示线性回归模型的自变量集合，Y表示线性回归模型的因变量，β表示偏回归系数，ε表示模型拟合后每一个样本的误差项.

为了求解线性回归模型的参数，将该模型的目标函数表示为^[16]

其中：λ为目标函数的惩罚系数，‖β‖₁和‖β‖₂²分别表示回归系数β的l₁和l₂正则项. 该目标函数由最小二乘误差平方和与正则项组成. 当λ=0时，该目标函数退化为MLR的目标函数；当λ≠0，α=0时，该目标函数退化为Ridge的目标函数；当λ≠0，α=1时，该目标函数退化为Lasso的目标函数. 对于Ridge和Lasso回归而言，寻找合理的λ值是平衡模型方差和偏差的关键. MLR的目标函数通过最小二乘误差平方和的方法获得；Ridge是一种替代最小二乘的压缩估计拟合方法，通过正则化减少方差，能够将系数向零的方向进行压缩，在MLR中实现变量重要性的筛选；Lasso也是通过正则化减少方差，与Ridge的差异在于Lasso可以将系数压缩至零，能够实现变量的筛选，得到输出参数较少的稀疏模型^[21].

对于比较复杂的非线性回归模型，需要在因变量和多个自变量之间构建复杂的非线性关系. 机器学习的非线性回归算法主要包括K近邻(k-nearest neighbor，KNN)、支持向量机(support vector machine，SVM)、决策树(decision tree，DT)、随机森林(random forest，RF)、梯度提升树(gradient boosting decision tree，GBDT)以及极端梯度提升(extreme gradient boosting，XGBoost)算法. 本文将以上非线性回归算法分为3类：递归划分方法、黑箱方法和集成学习方法^[22].

递归划分方法主要包括决策树(DT)算法. 该算法按照一定的规则持续拆分数据，每次将数据划分为两个相对一致的子集，直到达到目标，从而形成树状结构，直观反映变量的重要性，但该算法结构不稳定，容易产生过拟合的现象.

黑箱方法包括K近邻算法(KNN)以及支持向量机(SVM)算法. 这类算法的输入到输出过程是通过一个模糊的“箱子”进行处理. KNN通过比较已知样本和预测样本的相似度，寻找最相似的k个样本作为未知样本的预测. 采用多重交叉验证法选取最佳k值. SVM利用某些支持向量构成的“超平面”，将不同类别的样本点进行划分，SVM算法与其他单一的算法相比，能够将低维不可分的空间转化为高维的线性可分空间，具有较高的预测准确性，但其最大的缺点是容易受共线性影响，运算成本高. 这类方法对数据缺失较敏感，处理大规模数据的效率较低.

集成学习方法通过选择某种结合策略将若干弱学习器集合起来，以得到一个预测效果较好的强学习器. 随机森林(RF)、梯度提升树(GBDT)以及极端梯度提升(XGBoost)算法是一类以决策树(DT)为基学习器的集成学习算法. RF采用多棵决策树的投票机制，即将多棵树的回归结果进行平均，最终得到样本的预测值. 类似的，GBDT也是通过对多棵树的结果进行综合，不同的是每棵树是从之前所有树的残差中学习的，并以新树每个叶子的信息增益来进行最后的全局预测. XGBoost采用了随机森林的思想，作为升级版的GBDT算法，XGBoost使用损失函数的一阶导和二阶导作为残差的近似值，而GBDT仅利用损失函数的一阶导作为残差的近似值. 集成学习方法通常优于单一的回归方法，但预测速度明显下降，随着学习器数目的增加，所需的存储空间也急剧增加^[23].

通常采用线性回归模型以及非线性回归模型进行预测时，需要将不同模型的运行时间成本和准确率进行对比分析，从中选择合理的模型进行预测. 本文将准确率作为衡量标准，选择较优的模型对串联排队系统的平均等待时间进行预测.

为了生成机器学习所需的训练集数据，首先对串联排队系统进行模拟，得到不同参数下串联排队系统的平均等待时间.

将参数C_a²，E(S₁)，E(S₂)，C_S1²，C_S2²，ρ作为模型的输入参数，使用MATLAB对图 1所示的串联排队系统进行模拟，其中参数取值如表 1所示. 为了生成机器学习所需的训练集数据，使用表 1所列的参数范围，模拟了11 494种不同参数组合下的串联排队系统，其中相邻顾客的到达时间间隔和每个站的服务时间均服从伽马分布.

对于每个串联排队系统，模拟运行30个样本，每个样本取第400 001个顾客到600 000个顾客在第1个站和第2个站的等待时间的平均值分别作为第1个站和第2个站的平均等待时间，其中平均等待时间的置信水平大于95%，保证了模拟数据的可靠性.

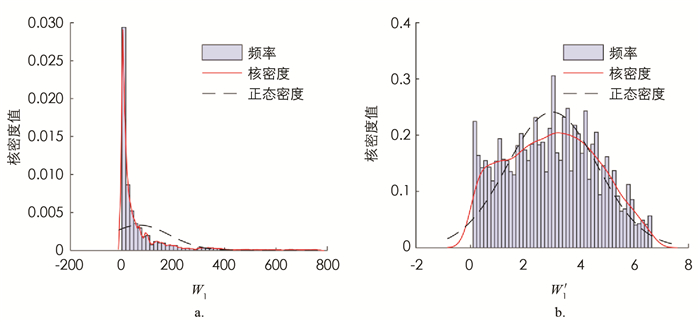
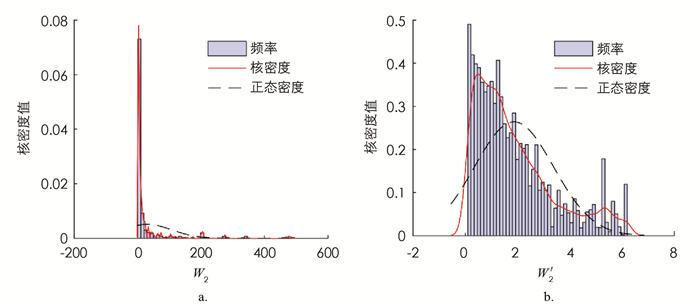
在对训练集数据进行建模分析之前，需要对数据进行预处理以满足模型的要求. 对于等待时间非常小的数据，即使预测值只有微小的偏差，其相对误差也会非常大，造成整体的平均误差偏大，影响预测效果. 因此，本文选取第1个站和第2个站的平均等待时间均大于0.1的数据进行分析. 从图 2和图 3的分布来看，模拟得到的串联排队系统的第1个站和第2个站的平均等待时间均呈现严重的右偏现象，为了满足机器学习模型的数据要求，提高模型精度和训练效率，本文对第1个站的平均等待时间W₁和第2个站的平均等待时间W₂分别进行对数处理，令

计算模拟得到的数值W_i和W′_i(i=1，2)的核密度如图 2，3所示. 从图中可知经过对数处理后，W′₁的分布近似服从正态分布，W′₂的右偏现象明显有所缓解，W′_i，i=1，2的值域均缩小到[－2，8]之间，采用W′_i加快了梯度下降求最优解的速度，即机器学习训练的速度.

本文采用python的sklearn程序包构建模型，将数据集按照85%和15%的比例随机分为训练集和测试集. 将具有两个站的串联排队系统的到达时间的平方变异系数C_a²、平均服务时间E(S_i)、服务时间的平方变异系数C_Si²以及瓶颈站的服务强度ρ作为特征，分别预测第1个站的平均等待时间W₁和第2个站的平均等待时间W₂.

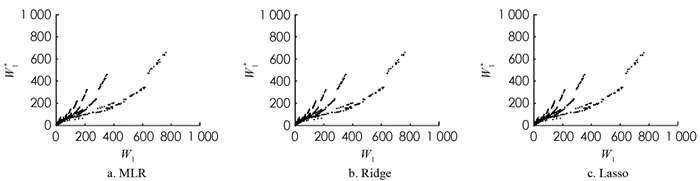
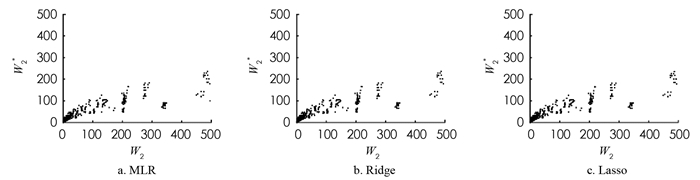
对于线性回归模型，即多元线性回归(MLR)、岭回归(Ridge)以及套索回归(Lasso)，利用10重交叉验证的方法确定最佳的λ值，如表 2所示. 基于最佳λ值使用训练集学习相应的线性回归模型，并对测试集进行预测. 基于线性回归模型预测的第1个站和第2个站的平均等待时间以及其模拟值如图 4，5所示，其中W_i，i=1，2表示第i个站平均等待时间的模拟值，W_i^*，i=1，2表示第i个站平均等待时间的预测值.

由图 4，5可知，MLR，Ridge和Lasso回归在W_i，i=1，2较小时的预测较准确，但对于平均等待时间较长的情况预测不准确. 为了定量的评估模型，使用平均相对误差$ r=\frac{\left|W_2-W_2^*\right|}{W_2}$来衡量模型的准确性，MLR，Ridge和Lasso回归对于第1个站的平均等待时间预测的平均相对误差分别为65.02%，65.03%，65.04%；对于第2个站的平均等待时间预测的平均相对误差分别为80.57%，80.57%，80.51%. 由此可知，3种线性回归模型对于串联排队系统的平均等待时间预测误差较大. 由于MLR，Ridge和Lasso回归均为线性回归模型，串联排队系统中顾客的平均等待时间与顾客的到达时间分布、服务器的服务时间分布等因素有着复杂的非线性关系，因此，使用线性回归对平均等待时间预测的效果不佳.

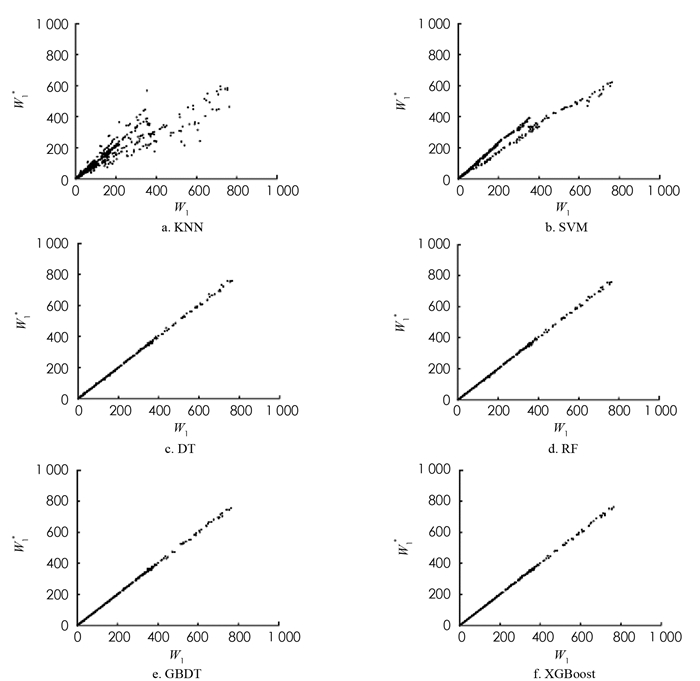
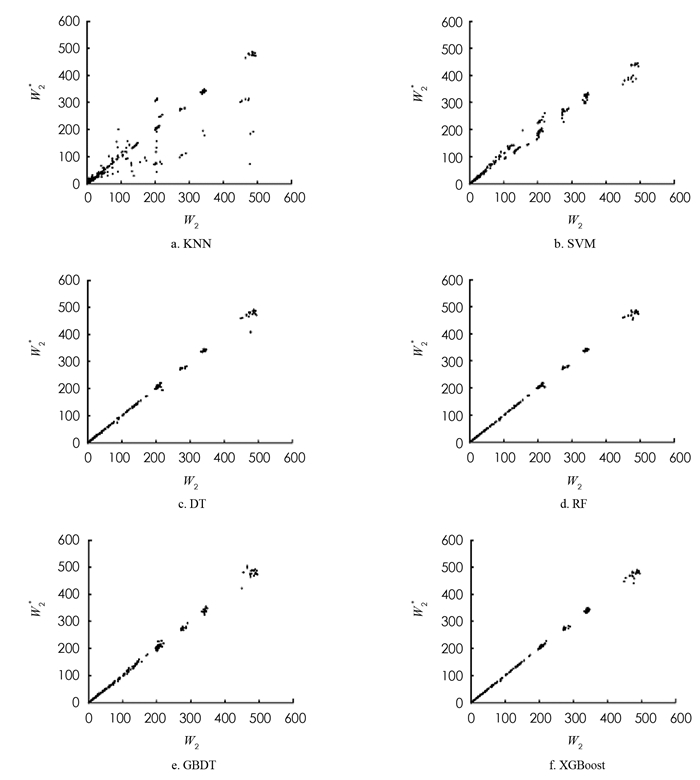
下面使用非线性回归模型对串联排队系统的平均等待时间进行预测，其中包括K近邻(KNN)、支持向量机(SVM)、决策树(DT)、随机森林(RF)、梯度提升树(GBDT)以及极端梯度提升(XGBoost)算法. 大多数机器学习算法都需要对参数进行设置，参数设置不同，学习得到的模型性能往往有显著的差异. 因此，使用非线性回归模型对平均等待时间进行预测时，需要对参数调优. 为了提高参数优化的效率，使用10重交叉验证的方法调整参数，并通过网格搜索找到最佳的参数组合. 各模型参数的范围和最优值如表 3所示，其中参数最优值(x₁，x₂)中x₁和x₂分别表示预测W₁和W₂所设定的模型参数.

对于上述非线性回归模型，使用最优的参数组合对训练集数据进行学习，并对测试集进行预测. 非线性回归模型预测的第1个站和第2个站的平均等待时间及其模拟值如图 6，7所示. DT，RF，GBDT以及XGBoost算法的预测效果明显优于KNN和SVM算法，这是由于RF，GBDT和XGBoost是基于DT的集成学习算法，结合了对所有弱学习器的预测，优于单一的学习器.

为了比较DT，RF，GBDT以及XGBoost算法的预测效果，将平均相对误差r作为模型的评价标准，4种模型的第1个站的平均等待时间的平均相对误差分别为3.42%，2.33%，2.79%，1.60%，第2个站的平均等待时间的平均相对误差分别为8.34%，4.13%，3.34%，1.86%. 实验结果表明，DT算法对于第2个站的平均等待时间的预测效果较差，XGBoost算法对第1个站和第2个站的平均等待时间的预测准确率分别为98.40%和98.14%，对串联排队系统的平均等待时间的预测较优.

目前，对于到达过程为更新过程，服务时间服从一般分布的排队系统的平均等待时间的研究均采用近似方法. 文献[24]研究了GI/G/1排队系统的平均等待时间. 文献[6]基于文献[24]的方法使用排队网络分析方法(QNA)研究了具有非马尔可夫性的串联排队系统的平均等待时间. 基于布朗运动，文献[7]利用一阶矩和二阶矩的近似方法提出了使用QNET方法估计串联排队系统中顾客的平均逗留时间.

为了验证本文方法的有效性，下面分别对GI/G/1-G/1系统以及M/G/1-G/1系统的平均等待时间的误差进行比较.

系统1：在GI/G/1-G/1串联排队系统中，假设相邻顾客到达时间间隔服从伽马分布，X~Gamma$\left(\frac{1}{5}, \frac{150}{\rho}\right) $，第1个站和第2个站的服务时间分别为S₁~Gamma$\left(\frac{1}{8}, 200\right) $，S₂~Gamma(2，15)，令ρ={0.1，0.2，…，0.9}.

系统2：在M/G/1-G/1串联排队系统中，假设到达过程为泊松过程，相邻顾客到达时间间隔服从指数分布$X \sim \exp \left(\frac{\rho}{30}\right) $，第1个站和第2个站的服务时间分别为$S_1 \sim {Gamma}(2,10), S_2 \sim {Gamma}\left(\frac{10}{9}, 27\right) $，令ρ={0.1，0.2，…，0.9}.

对于上述串联排队系统，分别采用Kingman方法以及本文提出的XGBoost方法对第1个站的平均等待时间进行预测；使用QNA，QNET以及本文提出的XGBoost方法对第2个站的平均等待时间进行预测，各种方法预测的相对误差如表 4，5所示.

由表 4可知，在不同的繁忙程度下，对于第1个站的平均等待时间，XGBoost方法、Kingman方法的平均相对误差分别为0.43%，28.02%. Kingman方法是对平均等待时间上限的近似分析，其预测效果比XGBoost方法差.

对于第2个站的平均排队时间，XGBoost方法、QNA方法以及QNET方法的平均相对误差分别为0.56%，30.49%以及19.42%. 相比于其他方法，XGBoost方法的相对误差最小且平均误差均小于1%. 在繁忙程度ρ较小时，顾客的平均等待时间较短，相对误差较大. 由此可知，本文提出的XGBoost方法明显优于其他方法，并且在繁忙程度ρ较大时，预测效果最佳.

在M/G/1-G/1排队系统中，第1个站的平均等待时间存在精确解析表达式，因此，仅对第2个站的平均等待时间的相对误差进行比较. QNA方法、QNET方法均通过考虑离去过程的一阶矩和二阶矩来刻画串联排队系统中第1个站对第2个站的影响. 虽然这些方法很容易计算平均等待时间的近似值，但是其计算的精确度不高. 由表 5可知，当ρ={0.1，0.2，0.3，0.5，0.6，0.8，0.9}时，本文提出的XGBoost方法相对误差最小，XGBoost方法、QNA以及QNET方法的平均相对误差分别为0.83%，4.58%以及3.55%. XGBoost方法的平均相对误差最小，QNET方法优于QNA方法，这是由于QNA方法在平方变异系数较大的情况下，参数分解方法的性能下降导致预测效果不佳^[7]. 综上所述，XGBoost方法优于其他方法，近似效果较好，能够比较准确地计算串联排队系统的平均等待时间.

本文采用机器学习中的线性回归算法和非线性回归算法预测串联排队系统的平均等待时间. 将仿真的通用性与机器学习的计算效率相结合，提高了平均等待时间预测的准确性. 大量的数值实验表明，XGBoost方法对平均等待时间的预测效果较好.

本文主要研究了两个站的串联排队系统，未来可以使用该方法对其他排队系统进行深入研究，例如具有多个服务站的串联排队系统、具有有限缓冲区的串联排队系统、具有批量服务的串联排队系统以及复杂的排队网络等.