研究选取中华人民共和国教育部制定的《普通高中数学课程标准(2017年版)》^[5](以下简称“课程标准”)和2020-2022年15套新高考试卷为分析对象.

评价与课程标准的一致性研究工具起源于美国，诺曼·韦伯(Webb)认为“一致性”是指各种事物之间相匹配的程度，即事物各要素之间相互融合形成一个和谐的整体^[6]. 安德鲁·帕特(Andrew Porter)和约翰·史密森(John Smithson)在吸收韦伯一致性分析模式的基础上，仅保留了一致性最核心的学习主题和认知水平两个维度来构建其研究矩阵，即SEC(Surveys of Enacted Curriculum)一致性分析模式^[7]. 由于其研究矩阵建立的自主性比较强，数据量化直观，并且可以借助Matlab软件中的函数运算得到具体的一致性指数及临界值^[8]，研究采取SEC一致性分析模式为研究框架. 据此，研究提出如下的分析过程：(1) 在“内容主题×认知水平”二维矩阵的框架下对新高考数学试题、课程标准进行编码、统计；(2) 对二维矩阵的数据进行归一化处理得到比率值，再将比率值代入Porter一致性系数公式，即得出两者的一致性程度，其中Porter一致性系数公式：

其中n是单元格总数，i表示任意单元格(1≤i≤n)，X_i和Y_i表示两个矩阵中对应的单元格比率值. 一致性系数p与一致性程度成正比(0≤p≤1)，p值越大一致性程度越高.

课程标准将课程内容划分为了预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动5个主题，但因“数学建模活动与数学探究活动”强调学生自主参与，试题对于此主题的考查通常与前4个主题知识相结合，因此，本研究只针对前4个主题进行分析.

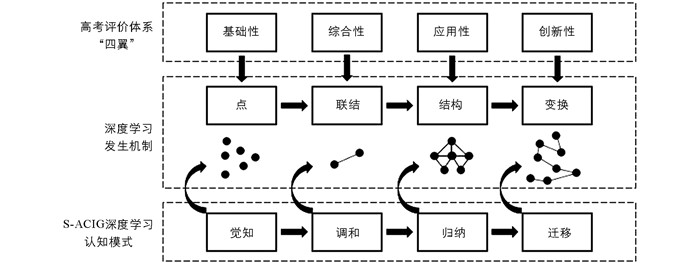
中国高考评价体系理论框架^[8]中“四翼”考查要求回答了高考“怎么考”的问题，其既是评价学生素质高低的基本维度，也是评价高考试题质量优劣的基本指标. 据此，研究以深度学习理论作为指导框架，参照深度学习品质测评工具^[9]，使“四翼”评价维度与深度学习发生机制^[10]成映射关系(表 1).

由表 1可知，“四翼”评价维度的命题要求与深度学习发生机制的4个阶段特征在划分的基本思想上具有一致性，在逻辑上具有匹配性，两者不同程度地融合了知识获取水平、实践操作要求、思维认知层次等学习品质，体现了从量变到质变对学习者深度发展水平的测量与评价，同时深度学习发生机制与S-ACIG认知模式存在如图 1所示的对应关系^[11].

对于数学认知水平，TIMSS^[12]发布了从知道、应用、推理3个维度考查数学认知能力的评价体系；沈南山等^[13]将数学认知能力水平划分为：知道事实、应用规则、数学推理和非常规问题解决4个层次；顾泠沅等构建了数学认知水平分析4层次框架，分别为：计算——操作性记忆水平、概念——概念性记忆水平、领会——说明性理解水平、分析——探究性理解水平^[14-15].

综合上述理论基础与分析结论，将数学认知水平划分为觉知、调和、归纳、迁移4个层级，每一层级的具体阐述、划分依据和对应课程标准的行为动词如表 2所示.

由此搭建出5×5二维矩阵，如表 3所示.

1) 课程标准编码

课程标准对每一个主题下的知识内容都做出详细的要求，依据行为动词对具体内容标准进行认知水平归类，建立“内容主题×认知水平”二维矩阵. 以“复数”这一节课标的内容要求为例，如表 4所示.

研究对课程标准编码结果进行统计，首先得到课程标准各主题内容与认知水平下的知识点数目，共146个知识点，再将原始数据进行归一化处理，得到其比率值，如表 5所示.

2) 对新高考数学试题的编码

与对课程标准的编码相似，参照2020-2022年新高考数学试卷及答案对数学试题进行编码，首先分析试题所考查的内容主题，再对应该主题下具体目标所考查的认知水平；其次按照评分标准对试题各解题步骤进行归类赋分并填入相应的二维矩阵单元格中，选择题与填空题也按解题步骤的权重进行赋分.

以2021年新高考1卷第5题为例：

已知F₁，F₂是椭圆C：$\frac{x^2}{9}+\frac{y^2}{4}=1$的两个焦点，点M在C上，则|MF₁| · |MF₂|的最大值为(     )

A. 13 B. 12 C. 9 D. 6

本小题为单选题，分值5分，具体解题步骤及编码过程见表 6.

按照上述方式对15套新高考试题进行编码，统计各试卷二维矩阵中每个单元格的分值，并进行归一化处理形成二维矩阵比率表. 上述试卷分析过程，由2名研究生和1名一线教师独立进行，出现分歧点通过讨论达成共识后再计算得出15套试题各主题、水平下的比率值. 以2022年新高考1卷为例，其内容认知分布比率如表 7所示.

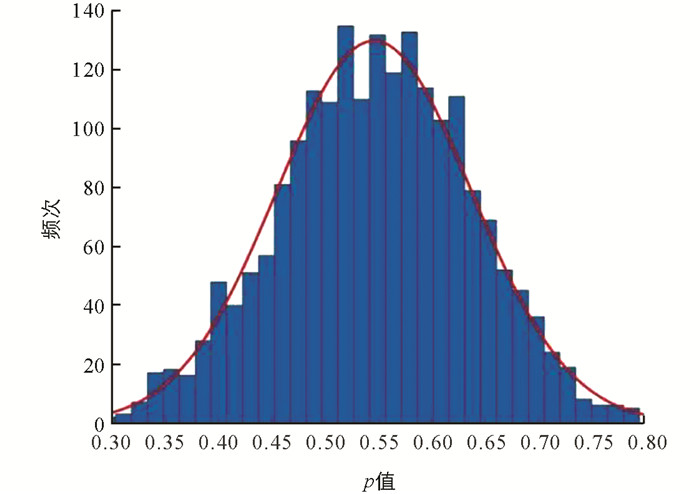
研究采用Matlab软件中的Unidrnd函数^[16]，将课程标准中146个具体内容随机赋值到一个4×4的矩阵A中，再将试卷总分150分随机赋值到另一个4×4的矩阵B中；对A，B两个矩阵进行归一化处理后得到相应的p值，重复此过程2 000次，即可得到一个关于p值的正态分布曲线；选取95%水平参考值为一致性系数p值的临界值，p值达到此临界值即具有统计学意义上的显著一致性，由此可以得出试卷与课程标准一致性表现良好的结论. 通过Matlab软件计算，得到研究p值的正态分布图(图 2)，判断p值是否具有显著一致性的临界值为0.717，即若试卷与课程标准的p值大于0.717，则试卷与课程标准具有显著一致性.

研究将课程标准数据比率表和15套新高考试卷比率表分别代入一致性系数公式中，计算15套新高考试卷与课程标准的Porter一致性系数如表 8所示.

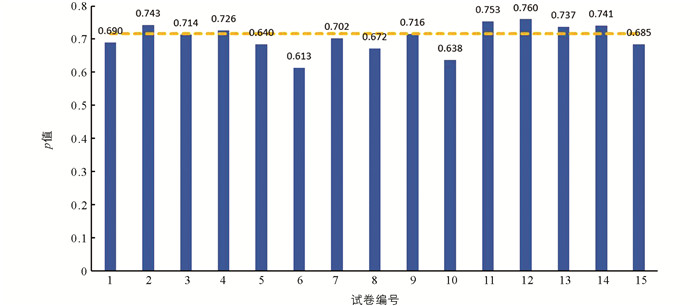
15套新高考试卷与课程标准的一致性系数如图 3所示，其中虚线表示0.717，即具有统计显著性的参考值.

由图 3可知：①仅有6套新高考试卷(2022年新高考2卷、2022年天津卷、2020年新高考1卷、2020年新高考2卷、2020年北京卷、2020年天津卷)与课程标准的一致性高于0.717，即具有统计学意义上的一致性，其他试卷并没有达到统计学意义上的一致性. ② 15套新高考试卷与课程标准的一致性系数均在0.6~0.8的区间，其中最大值为0.760(2020年新高考2卷)，最小值为0.613(2021年新高考1卷)，平均值为0.705，其中9套试卷一致性系数高于0.7. 因此，研究选取的15套新高考试题与课程标准达到了一定程度的一致性.

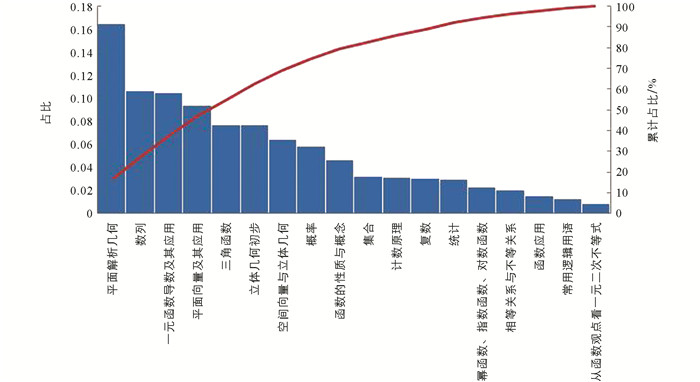
15套新高考试卷各细分单元的考查比例如图 4所示，其中“平面解析几何” “数列”“一元函数导数及其应用” “平面向量及其应用”等内容考查比例较高，总计接近总体的50%. “函数应用”“常用逻辑用语”“从函数观点看一元二次不等式”等内容考查比例较低，总计低于总体的5%.

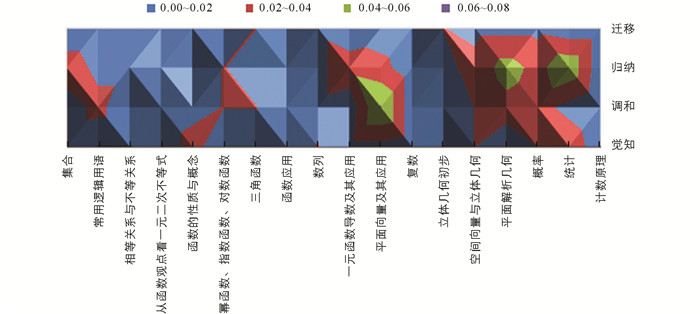
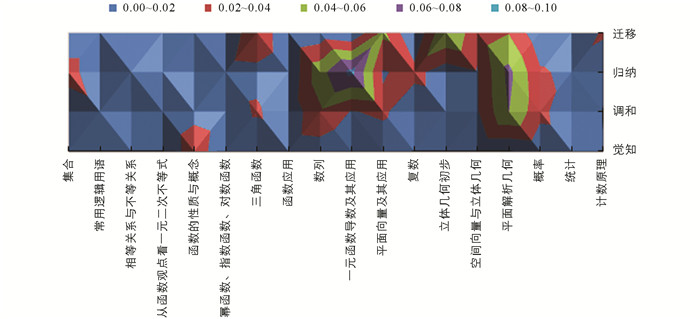
研究绘制了课程标准中每一主题下各单元与认知水平的曲面图，如图 5所示，更加直观地反映了各单元试题认知水平的差异. 不同的颜色代表不同的权重，图案代表不同范围值的区域，其中蓝色、橙色、灰色、黄色、深蓝色所代表的权重大小依次增大.

以4个认知水平为横坐标横向来看，橙色和灰色的区域主要集中在“调和”与“归纳”的区间，由此可见，课程标准中对“调和”与“归纳”两个水平的要求较高. 以18个小单元为纵坐标纵向来看，课程标准对“几何与代数”主题的考查权重及认知水平要求更高，特别是“平面向量及其应用”的“调和”水平呈现黄色，其比率值达到0.062，说明课程标准对其的重视程度. “几何与代数”主题涉及几何直观与数学运算等核心素养，要求学生通过数与形的结合，感悟数学之间的关联，在整个高中数学的学习中具有承上启下的作用.

图 6为新高考试题各单元与认知水平的曲面图，彩色区域集中在上半部分，由此可见，新高考侧重于对“归纳”和“迁移”两个水平的考查.

对比图 5与图 6，颜色匹配度较低，说明新高考试题与课程标准一致性较差，新高考试题的考查水平总体是高于课程标准要求的，难度偏高. 对比两图各单元情况，新高考中对于“数列”“一元函数导数及其应用”“平面向量及其应用”等内容考查水平明显高于课程标准的要求，而对于“常用逻辑用语”“统计”等内容的考查是低于课程标准要求的，这说明新高考试卷对核心且难度较大知识的考查比例较高，而对基础且较为容易知识的考查比例较低，总体难度高于课程标准要求. 下面分别从认知水平与内容主题两个维度对新高考试题与课程标准的一致性进行分析.

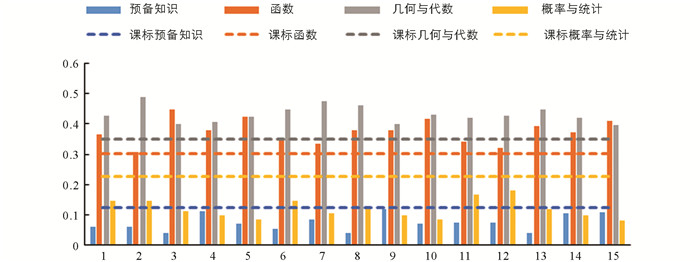
研究以柱形图直观地呈现了15套新高考试卷中各主题的比率，如图 7所示，4条虚线表示4个主题在课程标准中的占比情况，其数值分别为0.123，0.301，0.349，0.226；新高考试卷考查情况与之相同，对几何与代数、函数两个主题的考查比例较大，分别为43%与37%，而对预备知识、概率与统计两个领域的考查比例较小，二者之和仅占20%. 课程标准中4个主题的比重差异较小，极差为0.226，而试卷所对应的考查比重差别相对较高，极差达到0.357. 与课程标准相比，“函数” “几何与代数”两个主题的考查比率较高，“预备知识” “概率与统计”两个主题考查比率较低.

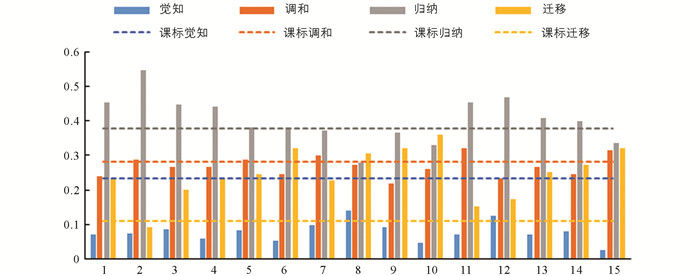
研究将每一水平在15套新高考试卷与课程标准中的比率以图 8柱形和虚线的形式表示，以便对新高考试卷与课程标准在认知水平上做出更加直观的比较，其中虚线是课程标准中各认知水平的占比，其数值分别为0.233，0.281，0.377，0.110. 从课程标准要求上来看，“归纳”水平比率最高，其次是“调和”与“觉知”，两者差别不大，“迁移”水平最低. 15套试题处在“觉知”和“调和”水平的试题比例约为35%，低于课程标准的要求，处于“归纳”和“迁移”水平的试题比例约为65%，高于课程标准的要求.

本研究以2020-2022年15套数学新高考试卷为例分析了新高考数学试题与课程标准的一致性程度，通过实证方法对基于课程标准命制的新高考试题与课程标准要求的一致性程度进行了验证，也能够从一定程度上反映出课程标准对新高考试题命制要求的落实情况.

15套新高考试卷与课程标准一致性不够高，其中仅6套试卷具有统计学意义上显著的一致性，由数据分析可得：①新高考1卷、2卷比地方卷一致性程度高；②地方卷一致性水平由高到低依次是：天津卷、北京卷、浙江卷；③ 3年新高考试卷与课程标准的一致性水平由高到低依次为：2022，2020，2021.

究其原因，课程标准是教育教学的基础性文件，其中规定了学生数学学习的基础目标，而高考是选拔性考试，其命题需具备一定的区分度，因而导致试题与课程标准的一致性水平不高，即高考试题的考查层次高于课程标准的要求. 课程标准中明确指出“高考命题应依据学业质量标准和课程内容”，因此，高考命题应在兼顾一定选拨性的基础上，尽可能地贴近课程标准中课程内容的要求. 内容主题决定试卷的“面积”，认知水平决定试卷的“高度”^[17]，在不分文理的新高考背景下，需要在兼顾“面积”和“高度”的基础上适当降低试题难度^[18]，在充分理解课程标准要求的基础上注重契合课程标准以及对数学知识结构以及认知水平的考查，合理设计数学试卷结构，以测评数学学科核心素养为目标，充分发挥出高考的导向作用.

观察15套新高考试卷与课程标准在4个主题的分布与权重图，得到结论：①各主题在15套试卷与课程标准中的分布情况一致；② 15套新高考试卷对“函数”和“几何与代数”主题考查情况远高于课程标准的要求，而对“预备知识”和“统计与概率”主题的考查力度不够，这也体现了高考试题的选拔性功能.

与传统的高考相比，新高考在考查载体、考查形式等方面进行了相应的调整，在重点考查基础知识和技能等显性知识的同时，逐步强化对数学思想方法、应用意识、理性思维、数学学科观念和知识迁移能力等隐性知识的考查，在此基础上需把握好各主题间的平衡关系，确保知识覆盖面足够广，从而考查学生知识掌握及运用的综合能力.

观察15套新高考试卷与课程标准在4个认知水平上的比率分布情况，得到结论：①各认知水平在15套试卷(从高到低依次为：归纳、迁移、调和、觉知)与课程标准(从高到低依次为：归纳、调和、觉知、迁移)中的分布情况存在差异，主要体现在新高考对迁移水平的考查远高于课程标准要求，突出考查学生将多个数学对象综合运用到新的数学情境中的能力；②二者均重视对归纳水平的考查，即要求学生理解归纳数学对象的本质.

当前的课程标准在内容主题上所覆盖的“广度”具有相当明确的规定与要求，但是在知识“深度”即认知水平划分上较为粗略，并未将每个行为动词的教学程度做出具体的界定，这使得教师和命题人难以把握教学的深度和试题的难度，因而导致试卷与课程标准的一致性产生偏差.

高考是我国人才选拔的重要方式，试题的质量关乎教育高质量发展水平. 新高考试题应当在保证试题基础性的同时，增加试题的区分度，通过对试题思维水平层次的把控，实现对不同层次学生的关注. 同时，构建科学的测评框架，制订合理的、细化的评价目标及评分标准，尽可能全面地衡量学生的数学学业水平，使新高考数学评价体系更为科学、完善，不断提升数学试题与课程标准的一致性. 学生的学业成就是课堂教学中教师与学生共同作用的结果^[19]，教师应当落实课程标准中的教学目标，依据深度学习的认知过程进行合理的教学活动，为学生提供良好的学习空间，促进其学习力的发展^[20]，提高学生问题提出与解决的能力，以激发学生的创造力^[21]，为实现中国教育现代化培养创新型人才.