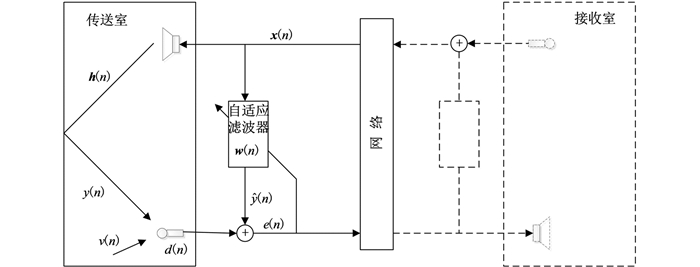
本文基于图 1所示线上会议系统的声学回声消除系统框图进行分析^[20]，输入语音信号x (n)经过回波路径滤波器为h (n)的发射室产生回波y (n)，该回波信号与加性噪声v (n)一起被麦克风拾取构成期望信号d (n). 声学回波路径由一个自适应有限脉冲响应(Finite Impulse Response，FIR)滤波器w (n) 建模，滤波器输出信号和麦克风输入端信号相比较，得到误差信号，通过最小均方误差代价函数对自适应滤波器的抽头系数进行调整，最终使包含期望信号的目标函数得到最小化值. 自适应滤波器w (n)与声学回波路径h (n)的长度L相同.

APA是一种数据重用算法，它不仅利用当前的输入矢量进行滤波器系数更新，而且重复利用过去的K-1个输入矢量，K为算法投影阶数. 假定输入噪声v服从均值为零，方差为σ²的高斯分布，APA的更新公式可由一个受线性约束的最小化表达式推导，即

式(1)中，w_i是自适应滤波器权重系数，后验误差矢量$\boldsymbol{e}_{i, p}=\boldsymbol{d}_i-\boldsymbol{U}_i^{\mathrm{T}} \boldsymbol{w}_i, \boldsymbol{d}_i=\left(d_i, d_{i-1}, \cdots, d_{i-K+1}\right)^{\mathrm{T}}$是期望信号，$\boldsymbol{U}_i=\left(\boldsymbol{u}_i, \boldsymbol{u}_{i-1}, \cdots, \boldsymbol{u}_{i-K+1}\right)$是K阶输入语音信号矩阵. APA算法中权重系数的第i次估计值w_i依据后验误差e_i，p为0的约束条件，把算法从有约束问题变为无约束的最优化问题^[21]，w_i可由式(1)解得

式(2)中，$\boldsymbol{e}_i=\boldsymbol{d}_i-\boldsymbol{U}_i^{\mathrm{T}} \boldsymbol{w}_{i-1}$是误差矢量. δ I是为了防止矩阵求逆时数据太大而添加的对角矩阵，δ是值很小的正数. 引入取值范围在0＜μ＜2的步长参数使算法收敛. 值得注意的是，当投影阶数仿射K=1时，APA算法等价于NLMS算法.

线上会议系统中的输入语音信号具有高度相关性，传统算法收敛速度明显降低，而APA算法具有降低相关的特性，输入语音信号严重相关时仍能快速收敛而不引起算法失调. 但是，算法在外界噪声影响下的鲁棒性能较差，算法性能严重衰退. 为了克服对自适应滤波算法的不利影响，文献[11]提出了仿射投影符号算法，基于l₁范数的符号函数APSA算法在某种程度上可以视为APA与符号算法的结合，算法描述如下所示：

式(3)-式(7)中，‖ · ‖₁是矢量的l₁范数，γ是将约束条件改为无约束代价函数时引入的拉格朗日乘子，sign(·)是符号函数. 由于后验误差矢量e_i，p在实践中无法获得，将其替代为近似的先验误差矢量e_i.

凸组合技术是一种组合因子的迭代方法，为工程实践提供了很好的解决方案. 与APSA固定步长方案不同的是，CC-APSA算法应用凸组合技术独立运行两个不同步长来同时满足自适应滤波算法对高收敛速度和低稳态误差的需求. 其中一个用大步长μ₁来保障算法的快速收敛，另一个用小步长μ₂来保障算法的低稳态误差. 最终CC-APSA算法性能优于其中任何一个步长的自适应滤波算法. 算法的整体输出表示为

式(8)中，$y_{1, i}=\boldsymbol{u}_i^{\mathrm{T}} \boldsymbol{w}_{1, i-1}, y_{2, i}=\boldsymbol{u}_i^{\mathrm{T}} \boldsymbol{w}_{2, i-1}, \boldsymbol{w}_{1, i-1}$和$\boldsymbol{w}_{1, i-1}$分别是大步长和小步长的滤波器权重系数. 组合因子λ_i根据整体误差矢量更新，即$\boldsymbol{e}_i=\boldsymbol{d}_i-\boldsymbol{y}_i$，采用文献[15]中的方法表示为：

式(9)中，α_i的自适应更新基于最小误差l₁范数采用梯度下降方案求出，即

式(10)中，μ_α是α_i的自适应更新步长，文献[15]建议α_i应被限定在对称区间[-α⁺，α⁺]内，并指出将其设定为4是合适的选择. 因此，修改式(4)得到CC-APSA算法的更新公式为

式(11)中，β是光滑因子.

线上会议系统中的双端讲话检测(DTD)是一个难点，基于信号包络检测的DTD是一种低运算量的算法，该方法通过比较远端语音信号和近端麦克风信号的能量进而作出相应的DT判断^[22]. 这点和Geigel方法性质类似. 但是，Geigel方法比较的是单个数据点的绝对值，检测函数的变化非常剧烈. 为了得到更准确稳定的判据，信号保罗检测法采用的是信号能量而非单个数据点. 通过IIR滤波平滑的方式来计算信号包络作为信号能量的度量，然后比较相关的估计值得出DT判断. 其中，输入语音信号能量为：

式(12)中，α=0.99是遗忘因子，麦克风信号能量为：

检测函数因此可以计为

式(14)中，参数γ在只有背景噪声时用来限制检测函数的取值，一般设为0.05. 通常情况下，回波能量相对于远端语音信号能量较弱，且近端语音信号能量比回波能量高. 因此，检测函数的值会随着DT出现而显著增大，并随着DT结束而减小. 将检测函数值和一个阈值T相比较，就可以做出相应的判断. 由于语音信号的能量具有时变特性，固定阈值T方案不是好的选择，必须设计一个能跟踪信号能量变化的时变阈值T(n). 当自适应滤波器收敛后，其输出y(n)可以近似地认为等同于真实的回波，因此可以用来作为时变阈值的参考，于是有：

式(15)中，κ=0.02是一个小的正数，用来为检测误差留下一点余地. 比较两者的值可以给出DT判断. 其中，v_x(n)的作用可看作是为了增加算法准确度引入的一个归一化处理.

本节提出一种新的凸组合仿射投影符号算法NCC-APSA(Novel Covex Combination Affine Projection Sign Algorithm)，新算法用新的非线性Sigmoid函数类型替代原算法中的sign函数，在第2部分双端讲话干扰推导基础上定义新的DT统计量g(n)，有效克服线上会议系统中的双端对讲干扰和脉冲噪声干扰，而且在收敛速度、稳态失调等方面依旧保持良好性能. 根据滤波器线性约束最小化表达式改写为代价函数形式为：

利用负梯度最陡下降法，对式(16)两边关于w_i求导：

令

代入约束条件和基于l₁范数的凸组合技术，然后代入式(10)组合因子推导结果，更新公式为：

为了保证算法在脉冲噪声下的鲁棒性，将式(18)改进为更加平稳的非线性函数sigmoid形式，在算法实施时，为了克服双端对讲干扰，本文做了一点处理. 定义新的DT统计量g(n)，采用ζ(n)-T(n)作为检测函数，通过试验设计固定阈值和控制环节来实现更稳定的DTD，改进后的权重系数更新为：

式(19)中，g(n)由如下表达式获得：

当单端讲话时，近端语音能量值非常小，即DT统计量g(n)=1. 在算法迭代初期，误差信号能量值较大，而滤波器输出信号能量和麦克风信号能量值较小，算法以大步长参数更新，收敛速度快的同时伴随着稳态误差不理想. 待算法迭代趋于稳定后，误差信号能量值变小，而滤波器输出信号能量和麦克风信号能量值逐渐增大，算法以小步长因子更新，降低稳态误差. 随着迭代次数不断增加，算法收敛程度增加，麦克风信号能量和滤波器输出信号能量的差值始终小于误差信号能量，由此可以保证式(19)推导的改进型仿射投影符号算法的收敛性. 当发生双端对讲时，近端语音能量快速增加到一个较大的值，即DT统计量g(n)=0，此时更新过程近乎停止，从而防止了算法发散. 当脉冲噪声干扰时由式(19)可知，会导致误差信号大幅度增加，从而造成$\mu_2 \boldsymbol{U}_i \operatorname{sigm}\left(\boldsymbol{e}_i\right) g(n) / \sqrt{\operatorname{sigm}\left(\boldsymbol{e}_i^{\mathrm{T}}\right) \boldsymbol{U}_i^{\mathrm{T}} \boldsymbol{U}_i \operatorname{sigm}\left(\boldsymbol{e}_i\right)} \approx 0$，权系数的增加量接近于零，算法的迭代几乎停止，因此基本消除了脉冲噪声对算法性能的影响，而回声抑制能力不受影响. 步长衡量因子满足文献[13]中提出的抗脉冲干扰条件. 步长调节因子在脉冲噪声发生时自动调节步长，算法性能趋于均方误差自适应算法，消除了权重矢量由于大幅度误差信号引起更新的可能. 以上分析表明，改进算法NCC-APSA在脉冲噪声和双端对讲的双重干扰下仍能保持算法收敛，表现出了复杂环境下良好的适应性.

本文基于MATLAB仿真平台对算法性能进行模拟，第1部分采用不同类型输入信号和系统脉冲响应分别分析APA算法、APSA算法、CC-APSA算法及NCC-APSA算法在收敛速度、均方误差和跟踪能力等方面的性能. 第2部分则验证改进型凸组合仿射投影符号算法在有双端讲话干扰的线上会议系统中的AEC性能.

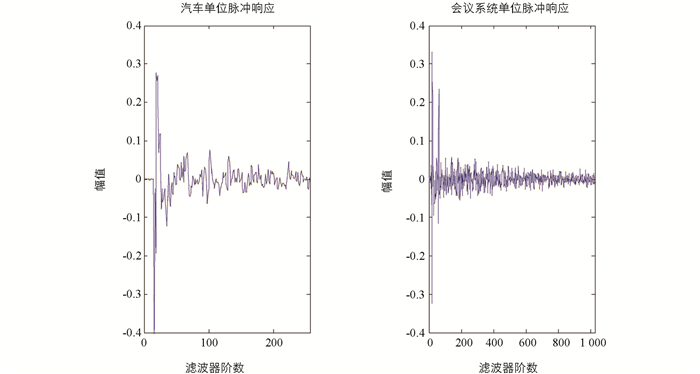
本节采用两种不同类型的远端输入信号进行仿真，8 kHz采样频率，16 bit量化. 输入信号如图 2是由零均值高斯随机信号通过AR模型T(z)=1/(1-0.7z)产生，信噪比SNR=30 dB. 图 3是仿真中系统辨识采用的两种不同单位脉冲响应，左边是截断长度为256阶的汽车单位脉冲响应，右边是会议系统中常见的1 024阶单位脉冲响应. 两种脉冲都不属于典型的稀疏信道，稀疏度分别为0.52和0.32. 衡量算法性能的指标为归一化均方偏差(Normalized Mean Square Deviation，NMSD)^[23]，用于度量自适应滤波器与目标系统的逼近程度，即回声抑制能力，其定义如下：

归一化均方偏差包括稳态误差和收敛速度两个跟踪性能，稳态误差越小，代表回声抑制效果越好，而收敛速度代表算法需要多少次迭代才能达到理想的回声抑制效果. 本文所有仿真曲线均是通过50次独立实验求平均值获得.

输入图 2中自回归模型下的高斯白噪声，期望信号由图 3的真实单位脉冲响应产生，无输出噪声.

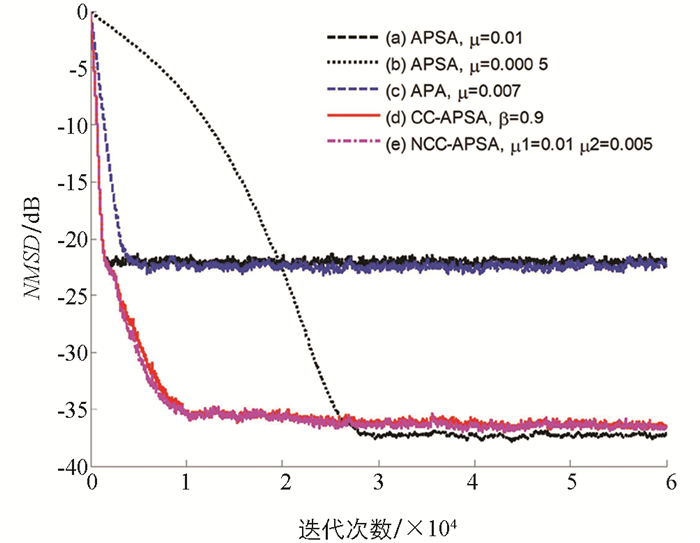
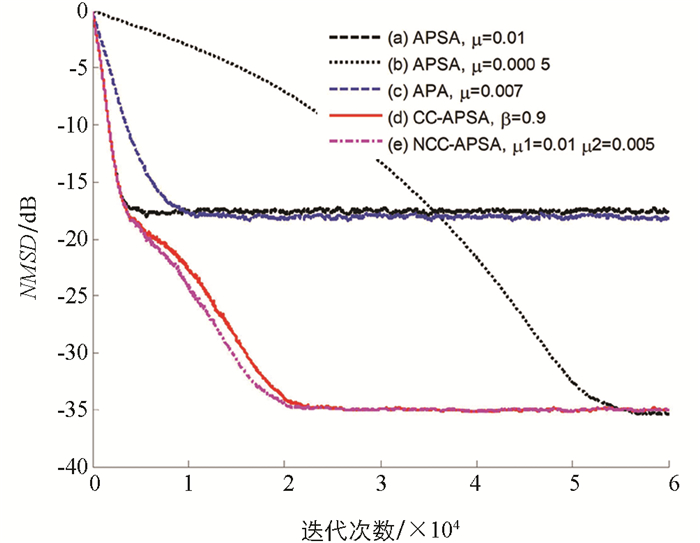
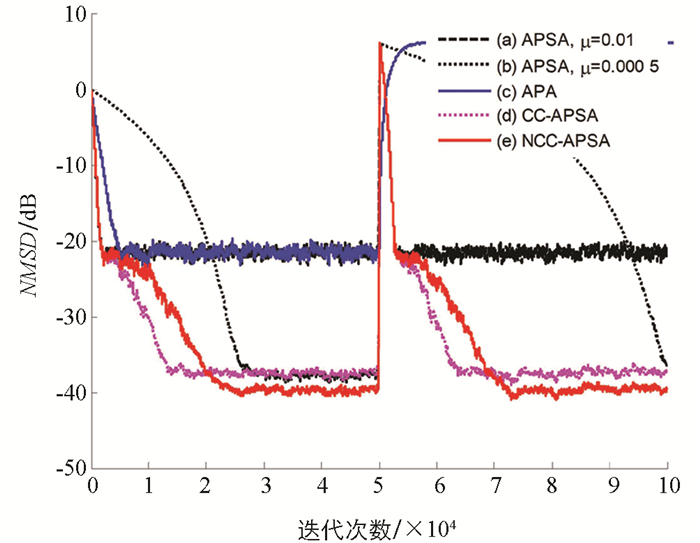
作为第一步，本文仿真了APA算法、APSA算法、CC-APSA算法和NCC-APSA算法在自回归模型下的跟踪性能，图 4和图 5分别展示了L=256和L=1 024两种系统辨识的情况. 实验结果表明，所提出的NCC-APSA算法具有优秀的收敛速度和稳态误差，当滤波器大小L=256时，CC-APSA算法和NCC-APSA算法无论是收敛速度还是稳态误差都好于APA算法、APSA算法. CC-APSA算法和NCC-APSA算法收敛速度相似，有几乎相同的稳态NMSD，都是大约900次迭代后开始收敛. 当L=1 024时，各算法性能均有不同程度的下降，算法无法达到900次迭代的稳态，但是可以看出CC-APSA算法跟踪性能略微优于NCC-APSA算法.

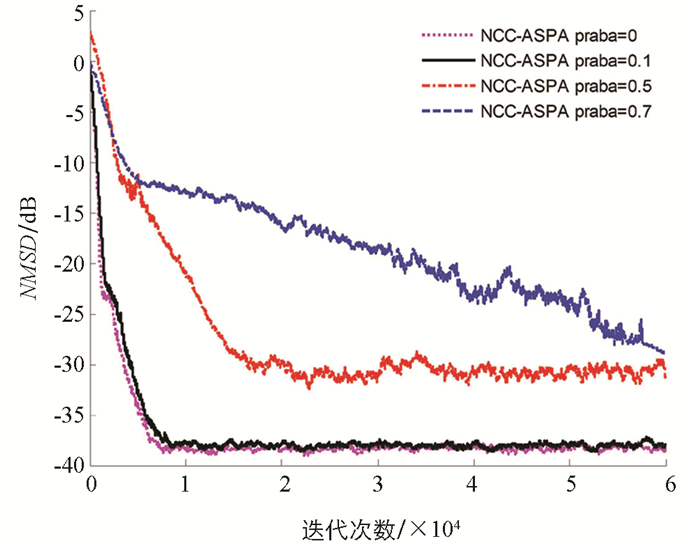
图 6和图 7是算法在期望信号中加入两种不同类型脉冲噪声后的跟踪性能曲线，利用混合高斯模型对脉冲噪声进行仿真^[24]. 模型为k_iA_i，k_i为伯努利过程P[k_i=1]=praba，其中praba表示该过程中冲激噪声的出现概率. A_i为零均值，功率为σ_A²=1 000σ_y²的高斯随机过程，从图 6可以看出，NCC-APSA算法在冲激噪声逐步增大的情况下，虽然误差增大，但是仍然保持了稳定性，因而验证了NCC-APSA算法对一般冲激噪声具有很好的通用性和鲁棒性. 图 7中冲激响应在第50 000次迭代时从w突变为-w，本文主要观测算法的收敛和跟踪性能，在冲激噪声下NCC-APSA算法不仅收敛，而且在未知系统发生截断误差后算法很快跟上了系统变化，可见系统突变对NCC-APSA算法未损失收敛速度和稳态误差性能.

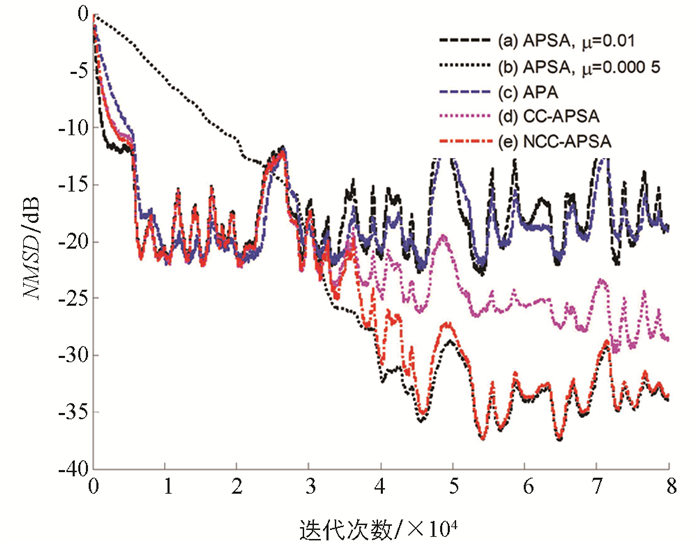
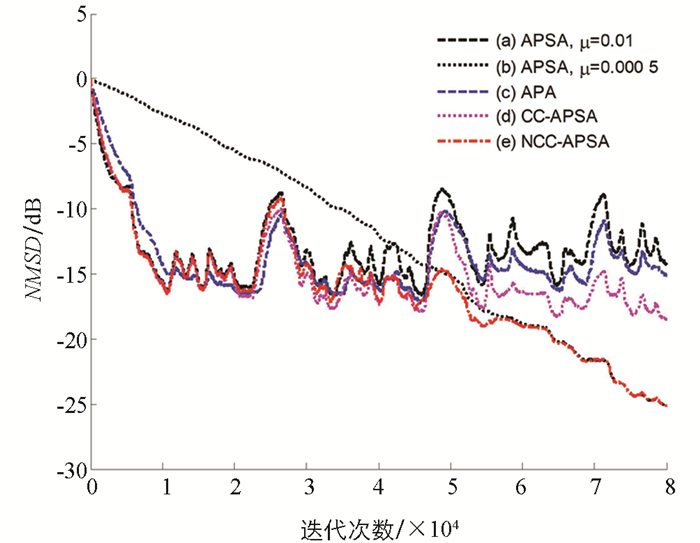
语音由于具有非平稳特性和频谱范围大的特点而非理想的脉冲响应激励信号^[25]，在实际应用场景中，输入信号往往是语音信号而非高斯白噪声，所以本文采用真实语音信号进行仿真实验，材料取自一段中文男声，具有10~30 ms的准稳态特性及高相关性. 本文对NCC-APSA算法使用语音信号作为输入信号进行了对比实验，分别采取图 4所示的两个单位回声脉冲响应进行滤波. 对于这两个实验，本文都添加一个信噪比为50 dB的高斯白噪声成分. 图 8和图 9分别显示了长度为L=256的汽车系统和长度为L=1 024的线上会议系统的结果. 与APA、APSA和CC-APSA算法相比，NCC-APSA算法在暂态和稳态状态下都具有良好的AEC性能.

为了进一步验证NCC-APSA算法的性能，本文采用真实语音信号进行线上会议系统的回声消除实验，分别在两个不同房间进行音频数据采集. 两个房间分别配置了不同的普通家具家电，发送室大小约为4.35 m×3.2 m×2.8 m(L×W×H)，接收室大小约为3.8 m×2.6 m×2.5 m(L×W×H). 用于语料采集的器材包括电脑、麦克风和扬声器等，扬声器和麦克风分别摆放在电脑两侧，且两者距离0.45 m左右. 电脑摆放在中间负责数据处理，麦克风录制远端语音信号，远端信号经过房间的回声信道形成回声后被麦克风拾取，同时被拾取的还有近端信号和环境噪声(图 10).

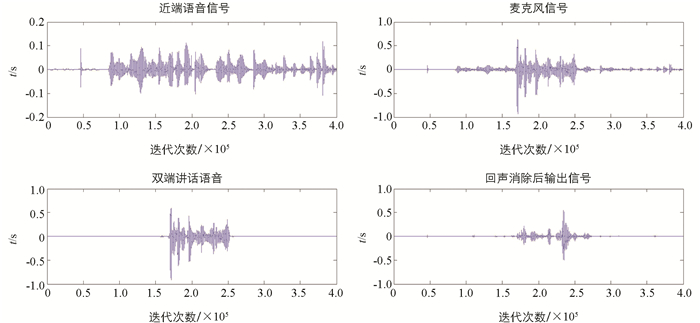
近端讲话的语音内容是一段中文男声“园林采用新中式建造手法……”，语音数据的采样率设置为8 000 Hz，根据房间实际脉冲来选择截断长度，确定自适应FIR滤波器阶数L=1 024阶. NCC-APSA算法处理结果如图 11所示，左边是近端语音信号(长度设置为400 000)和双端讲话语音的时域波形图，语音信号在迭代次数为156 800时加入双讲语音，其余设置为0，无双端对讲影响. 图 11右侧从上往下分别是麦克风信号和回声消除后的输出信号时域波形图. 从图 11中可以看出，NCC-APSA算法可以有效地滤除回声干扰噪声，听感方面的回声抑制效果也很好，工程实践中具有很高的实用价值.

针对线上会议系统中存在的双端讲话干扰和脉冲噪声问题，本文提出一种适用于线上会议系统的改进型仿射投影符号算法. 仿真结果表明，该算法可以有效克服线上会议系统中的双端对讲干扰和脉冲噪声干扰，而且依旧保持良好的跟踪性能. 尽管本文算法在一定程度上改善了算法性能，但是没有考虑稀疏信道下的性能优化，而且计算复杂度依然较高，不利于实际应用中推广. 因此，如何利用信道的稀疏先验特性，进一步开发适应稀疏信道的低复杂度算法是下一步研究的重点工作.