-
开放科学(资源服务)标识码(OSID):

-
近年来,水稻插秧机在自动化、高效率、多功能和智能化等方面不断发展[1-2],高速旋转式水稻插秧机秧箱的平均冲击载荷是曲柄摇杆式高速水稻插秧机的7倍,双螺旋轴会因受到较大的载荷而失效[3],直接影响插秧机移箱机构的稳定性、安全性和横向送秧的均匀性.因此,有必要对高速水稻插秧机双螺旋轴进行可靠性分析.
为提高双螺旋轴的稳定性,相关学者已开展大量研究工作.杨文珍等[4]通过优化双螺旋轴回转曲线以减少滑块对回转槽面的冲击,并通过有限元模拟验证所提出方法的合理性;赵匀等[5]优化螺旋轴的曲线并在双螺旋轴的两端施加缓冲弹簧装置以减少滑块对双螺旋轴两端滑道的作用力;蒲明辉等[6]通过优化双螺旋轴回转曲线以减少滑块对螺旋轴的作用力;褚婷婷等[7]用Kriging模型建立了双螺旋轴结构参数与振荡频率之间的关系,通过多目标分析优化了双螺旋轴的设计参数.以上研究表明,双螺旋轴主要失效部位为回转槽面,即回转槽面受到滑块的较大冲击而破坏.对双螺旋轴进行可靠性分析,关键在于建立影响参数与回转槽面失效形式之间的非线性关系,因此选择高效准确的可靠性分析方法[8-9]尤为重要.
采用传统方法进行双螺旋轴可靠性分析时,通常在试验机上对双螺旋轴进行直接破坏,并重复成百上千次,需要消耗大量的时间与经费.基于概率理论的Monte Carlo模拟法(MCS)[10-11]常用于可靠性分析中,虽然精度较高,但是需要大量样本、耗时长,且对于高非线性的物理模型效果不理想.为此,工程人员将代理模型法[12-13]引入到工程可靠性设计中,代理模型法仅需少量样本便能得到精确的可靠度.近年来,自适应Kriging模型结合Monte Carlo模拟的可靠性分析方法(AK-MCS)[14]被广泛应用到可靠性分析中.冯吉路等[15]将AK-MCS法应用到主轴系统振动可靠性分析中,减少了97.2%的有限元分析时间;罗文俊等[16]将改进AK-MCS法应用到船舶板架极限强度可靠性分析中,减少了38%的有限元模型调用次数;李娜等[17]将AK-MCS法应用到地下管线抗震可靠性分析中,分析时间仅为MCS法的2%;赵心怡等[18]将AK-MCS法应用到角接触球轴承刚度的可靠性分析中,物理模型调用次数仅为MCS法的0.048%;李正良等[19]将AK-MCS法应用到直立锁缝屋面系统抗风揭可靠性分析中,计算成本为MCS法的25.1%;刘玉敏等[20]将AK-MCS法应用到新能源电动汽车转向驱动桥空心半轴可靠性分析中,验证了AK-MCS法在效率和精度两方面均优于MCS法.以上研究中,AK-MCS法被应用到工程可靠性分析中,在满足精度的同时,计算时间相比MCS法减少一半以上,验证了AK-MCS法在工程结构可靠性分析中的高效性.本文旨在寻求进行双螺旋轴可靠性分析的高效准确方法,因此,AK-MCS法对双螺旋轴可靠性分析具有实用价值.
本文分析了双螺旋轴所受载荷情况,介绍了自适应Kriging模型结合Monte Carlo模拟的可靠性分析方法以及实现双螺旋轴可靠性分析的流程,建立了双螺旋轴有限元分析模型,考虑材料密度、工作载荷、工作温度3个参数对双螺旋轴回转槽面最大挤压应力的影响,并对其进行可靠性分析.最后与MCS可靠性分析方法进行对比,验证了本文所采用方法的高效性与准确性.
全文HTML
-
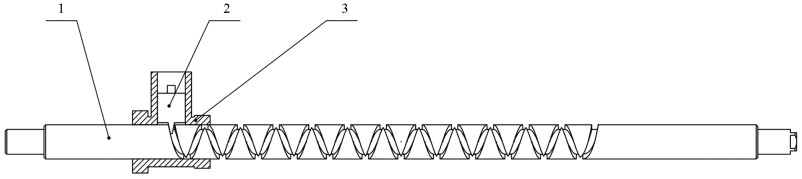
移箱机构(图 1)由双螺旋轴、滑块和轴套组成,是高速水稻插秧机的重要组成部分,工作原理是来自动力机构的转矩传送给双螺旋轴,双螺旋轴带动滑块和轴套左右移动,实现秧箱秧盘的左右移动,从而使分插机构的秧爪能够依次、均匀地在秧箱工作幅宽内完成取秧[21].移箱机构运动分两种,第一种为平动阶段,移箱机构水平移动推送秧箱和秧盘;第二种为急回阶段,移箱机构推送秧箱和秧盘换向.由于滑块在极短的时间内经历减速、转向、加速等过程,螺旋轴回转槽面将受到较大的冲击载荷.
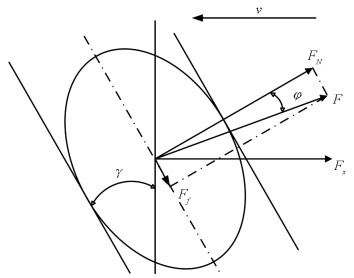
如图 2所示,在平动阶段,移箱机构的载荷主要来自秧箱与底盘的摩擦力Fx,滑块与滑道之间的摩擦力Ff忽略不计,φ为滑块与滑道之间的摩擦角.设秧箱与底盘的摩擦力Fx=μmg,所以在平动阶段,螺旋槽所受到的正压力FN1为:
式中:μ为秧箱和秧盘与机架的摩擦系数;m为秧箱和秧盘的总质量;γ为双螺旋轴的螺旋升角.
在急回阶段,螺旋槽所受到的摩擦力忽略不计,仅受正压力FN2为:
式(1)与式(2)中,FN1与FN2为FN在不同阶段的表现形式.
在急回阶段,滑块在短时间内经历减速、转向、加速等过程,此时对回转槽面的冲击力最大.当螺旋槽所受到的正压力超过槽面所能承受的最大载荷时,回转槽面破坏失效[4],槽面受到的挤压应力直接反映冲击载荷的大小.
温度也会影响双螺旋轴所受挤压应力的大小,具体数值受到多种因素的影响.在长时间工作后,移箱轴部分的温度会上升,可达到50 ℃左右.因此,双螺旋轴工作时,挤压应力会受到温度和载荷的双重影响.
-
基于自适应Kriging模型结合Monte Carlo模拟的可靠性分析方法是在建立Kriging模型的基础上,通过学习函数选取对失效面贡献最大的点,更新Kriging模型,最后通过Monte Carlo模拟法完成可靠性分析.
-
Kriging模型包括回归函数和随机分量,可用gK(x)表示为:
式中:fi(x)为回归函数的基函数;βi为回归函数的待定系数;z(x)为随机分量,定义在空间x(i)和x(j)的两点之间,具有均值为0和方差为σ2的平稳高斯过程.其协方差矩阵的分量可以表示为:
式中:R=(x(i),x(j)),i,j=1,2,…,m,表示任意两个样本点的相关函数,它是相关矩阵R的分量,m为训练样本的个数.R=(x(i),x(j))有多种函数形式可以选择,高斯型相关函数的表达式为:
式中:θk为未知的相关参数,k=1,2,…,m.
未知点x处的响应估计值为:
式中:
$ \boldsymbol{{\mathop\beta \limits^ \wedge }}$ 为回归函数待定系数估计值向量;g为训练样本数据的响应值构成的列向量;F表示具有输入参数样本的基函数m×p阶矩阵;r(x)为训练样本点和预测点之间的相关函数向量,可以表示为:依据最小二乘理论,待定系数向量
$ \boldsymbol{{\mathop\beta \limits^ \wedge }}$ 和方差估计值${\mathop {\sigma}\limits^ \wedge }^2$ 分别为:相关参数θ=(θ1,θ2,…,θm)T可以通过极大似然估计的最大值得到,即:
求解的θ值构成的Kriging模型为拟合精度最优的代理模型[21],用于表示输入变量与性能响应之间的函数关系.
-
U学习函数可以表示为:
式中:μgK(x)和σgK(x)分别为预测值的均值和标准差.对于样本点的U函数值,当gK(x)相同时,σgK(x)越大,U函数值越小;当σgK(x)相同时,gK(x)越接近0,U函数值越小.U函数值越小的样本所对应的{x,gK(x)}应加入到训练样本集中来更新Kriging模型.文献[14]认为,当U函数值大于等于2时学习完成.
-
根据自适应学习过程得到精确的Kriging模型,建立双螺旋轴可靠性分析的极限状态函数,其形式为:
式中:yallow为双螺旋轴回转槽面的许用应力值;gK(x)为双螺旋轴回转槽面的应力响应值;x为不确定输入参数的随机输入变量.
Monte Carlo模拟法是依据大数定律,结合随机输入变量x=[x1,x1,…,xn]T和通过Kriging模型预测得到的结构响应gK(x)=[gK(x1),gK(x2),…,gK(xn)]T进行分析,n为随机输入变量的数量.由式(13)可知,IF(x)为失效域的指示函数,当y(x)≤ 0时,指示函数的值取1,否则取0,故失效域为F={x:y(x)≤0},安全域为S={x:y(x)>0}.
失效概率的估计值
${\mathop P\limits^ \wedge }_f$ 为落入失效域内的样本个数NF与总样本个数N的比值,引入式(13)指示函数,则失效概率${\mathop P\limits^ \wedge }_f$ 和可靠度${\mathop P\limits^ \wedge} _r$ 分别为: -
步骤1 首先确定双螺旋轴的随机输入变量,根据数值特征(均值和标准差),采用拉丁超立方抽样(LHS)抽取m组输入样本建立MCS样本集NMC.
步骤2 建立双螺旋轴的有限元模型,从样本集NMC中随机选取n组样本,结合有限元仿真获得结构响应,建立初始训练样本集T,根据式(3)-式(10)建立初始Kriging模型.
步骤3 将MCS样本集NMC中的样本带入初始Kriging模型,并计算每个样本的U学习函数值U(x),将最小U(x)值的样本点作为下一个需要的样本点,更新Kriging模型.
步骤4 判断Kriging模型自适应性学习过程是否收敛.当min U(x)≥2时,结束学习过程,执行步骤5.若当min U(x)<2时,计算xu的响应值gK(xu),并将{xu,gK(xu)}加入到训练样本集T中,作为训练样本更新Kriging模型.
步骤5 利用当前Kriging模型计算样本池NMC中所有
${\mathop g\limits^ \wedge }_K(\boldsymbol{x})$ 值,并计算失效概率${\mathop P\limits^ \wedge }_f$ 和变异系数Cov(${\mathop P\limits^ \wedge }_f$ ).失效概率由式(14)得到,并根据Monte Carlo模拟法计算失效概率估计值的变异系数Cov(${\mathop P\limits^ \wedge }_f$ ),其形式为:步骤6 当Cov(
${\mathop P\limits^ \wedge }_f$ )<5%时,即认为${\mathop P\limits^ \wedge }_f$ 对Pf估计是可以接受的,结束AK-MCS过程并得到Kriging模型.通过该方法获得的概率估计值${\mathop P\limits^ \wedge }_f$ 即作为失效概率Pf,若当Cov(${\mathop P\limits^ \wedge }_f$ )≥5%时,重新执行步骤1,本次获得的样本数据仍可作为训练样本.基于AK-MCS法进行双螺旋轴可靠性分析的整个流程如图 3所示.
2.1. Kriging基础理论
2.2. U学习函数及停止准则
2.3. 可靠性分析
2.4. 双螺旋轴可靠性分析步骤
-
以某型号高速水稻插秧机双螺旋轴为例,在SolidWorks软件中建立双螺旋轴的三维模型,如图 4所示.
为减少计算时间,提高计算效率,仅建立滑块和双螺旋轴的三维模型,利用ANSYS Workbench划分网格,并生成双螺旋轴的有限元分析模型,网格采用三维四面体网格,节点数为142 665,单元数为82 033,划分结果如图 5所示.
双螺旋轴材料[22]选用45钢,密度为785 0 kg/m3,弹性模量为2.1×1011 Pa,泊松比为0.269,热膨胀系数为1.2×10-5 ℃-1.根据实际工况,双螺旋轴在长时间工作时,轴整体达到一定的温度,结合ANSYS Workbench热结构和静态结构对其进行热结构耦合分析,设置对应载荷和边界条件,执行确定性分析获得其最大响应值.分析结果如图 6所示,双螺旋轴的最大应力值点在螺旋轴回转部分槽面与滑块接触处,最大应力值为554.58 MPa.
-
由双螺旋轴响应分析可知,材料性能、载荷、螺旋轴工作温度影响了双螺旋轴回转槽面的最大挤压应力,故选取材料密度、工作载荷以及工作温度作为双螺旋轴可靠性分析的随机输入变量,考虑材料密度、来自滑块的压力和双螺旋轴的工作温度对双螺旋轴回转槽面最大挤压应力的影响,进行可靠性分析.随机输入变量的分布形式以及数值特征如表 1所示.
根据表 1数据,采用拉丁超立方抽样(LHS)抽取1×106组数据作为MCS样本池,并从中选择16组样本进行有限元仿真,获得双螺旋轴回转槽面挤压应力最大响应值,并建立训练样本集T.根据训练样本集T建立初始Kriging模型,回归模型为常数,相关模型为高斯型,经过主动学习过程后添加高效样本点8个,建立最终Kriging模型.
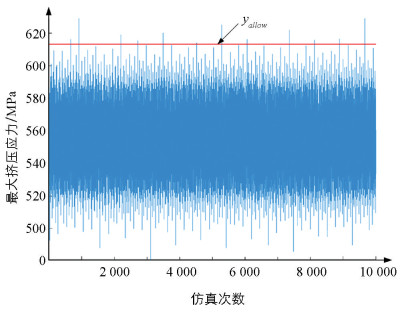
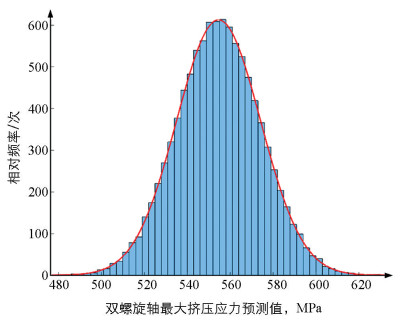
根据建立的Kriging模型进行10 000次仿真,获得了双螺旋轴最大挤压应力响应的仿真历史图和频率分布直方图,如图 7和图 8所示.双螺旋轴最大挤压应力服从均值为554.61、标准差为19.53的正态分布.根据3σ原则[23]可知,双螺旋轴最大挤压应力的许用值yallow=613.21 MPa,建立极限状态函数为:
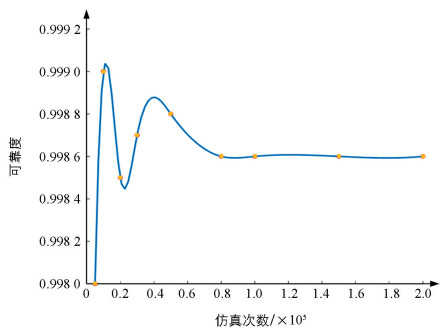
基于极限状态函数,结合MCS对不同样本规模下的双螺旋轴最大挤压应力进行可靠性分析.可靠性分析结果如表 2和图 9所示.可以看出随着仿真次数的增加,双螺旋轴受到最大挤压应力时可靠度收敛为一个定值0.998 6,且此时的变异系数Cov(
${\mathop P\limits^ \wedge }_f$ )=3.61%,满足计算要求.所以将0.998 6作为双螺旋轴最大挤压应力的可靠度. -
为验证基于AK-MCS的可靠性分析方法在进行双螺旋轴可靠性分析时的有效性,将本文方法与MCS法在仿真准确率和仿真效率上进行对比,2种方法(AK-MCS和MCS)分别进行500次、1 000次、3 000次、5 000次模拟,实现双螺旋轴最大挤压应力可靠性分析.为真实反应对比结果,有限元仿真和数值仿真均在相同计算环境中进行(CPU:Intel© CoreTM 12600KF,内存:16GB).
在仿真准确率上(表 3),根据多次模拟可以得出结果,基于AK-MCS的可靠性分析方法获得双螺旋轴最大挤压应力的可靠度与基于MCS法得到的结果基本一致,在3×103模拟水平上,相对准确率达到了99.98%,因此基于AK-MCS可靠性分析方法具有较高的准确率.
在仿真效率上(表 4),MCS法在500次水平上用时7 550 min,基于AK-MCS的可靠性方法得到可靠度用时362.4 min,在所用时间上是MCS法的4.8%.随着模拟次数的增加,AK-MCS可靠性分析方法的效率明显提高,在模拟次数为5 000时,AK-MCS可靠性分析方法的用时仅为MCS法的0.5%,原因在于AK-MCS可靠性分析方法仅需要24次仿真(初始样本和高效样本的仿真次数),且数值仿真时间远小于有限元仿真.因此,AK-MCS可靠性分析方法更高效.
综上所述,基于AK-MCS可靠性分析方法在进行双螺旋轴可靠性分析时,能够快速计算出可靠度且具有较高的精度,优势明显.
3.1. 确定性分析
3.2. 双螺旋轴可靠性分析
3.3. 结果分析
-
本文采用自适应Kriging模型结合Monte Carlo模拟的可靠性分析方法(AK-MCS)对双螺旋轴进行可靠性分析,考虑材料密度、工作载荷、工作温度3个参数对双螺旋轴最大挤压应力的影响,计算获得可靠度.得出以下主要结论:
1) 建立了双螺旋轴的有限元分析模型,通过热结构耦合分析得到了双螺旋轴的最大应力值为554.58 MPa,位置在回转槽面.
2) 基于AK-MCS方法建立了双螺旋轴最大挤压应力极限状态函数,并完成可靠性分析,在许用抗压强度为613.21 MPa条件下,计算出双螺旋轴的可靠度为0.998 6.
3) 将MCS法与自适应Kriging模型结合Monte Carlo模拟的可靠性分析方法在仿真效率上进行对比,本文采用的AK-MCS可靠性分析方法具有明显的优势.



 下载:
下载: