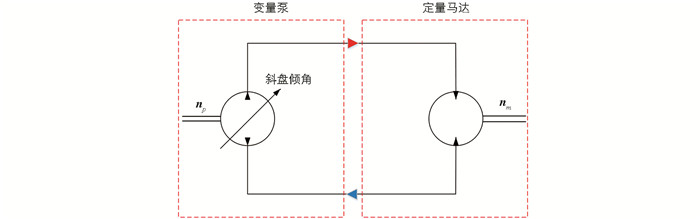
本文所采用的静液压变速器是变量泵-定量马达结构(图 1)，除泵和马达外，其他元件的结构和功能对HST的输出转速影响较小^[25]，通过调节变量泵的排量即可实现马达的转速控制.

变量泵的排量方程为：

式中：T_P为时间常数；q_P为泵的排量；k_P为泵的比例系数；u_P为泵的控制电压.

考虑油液泄露的变量泵流量方程为：

式中：Q_P为泵的流量；n_P为泵的转速；P为高压油腔压力；C_iP为泵的内泄露系数；C_eP为泵的外泄露系数.

定量马达的流量方程为：

式中：Q′_P为定量马达的流量；C_im为马达的内泄露系数；C_em为马达的外泄露系数；n_m为马达输出转速；q_m为马达排量；V₀为压力油腔总容积；β_e为油液的体积弹性系数.

马达转矩平衡方程为：

式中：J为马达负载折算到马达轴上的等效转动惯量；B为黏性阻尼系数；T_l为负载力矩.

联立式(1)-(4)，即可建立HST的状态空间方程为：

令x₁=q_P，x₂=P，x₃=n_m为系统的状态变量，则式(5)可写为

其中，$a_1=\frac{1}{T_P} $，$ a_2=\frac{\left(C_{i m}+C_{e m}+C_{i P}+C_{e P}\right) \beta_e}{V_0}$，$ a_3=\frac{\beta_e q_m}{V_0}$，$ a_4=\frac{\beta_e n_P}{V_0}, a_5=\frac{q_m}{J}, a_6=\frac{B}{J}, b=\frac{k_P}{T_P}$，$ d=\frac{T_l}{J}$.

由式(6)可知，除了HST内油液性质参数，马达转速的主要影响因素有变量泵的排量、马达负载力矩以及液压回路中油液的泄露，其中突变的外界负载在建模时作为附加项单独表示，油液泄露通过泄露系数表示，变量泵的排量则通过泵的斜盘倾角控制.

基于式(6)推导HST的状态空间方程为：

式中：x为中间变量矩阵；y为输出变量；f(x)、g(x)分别为与中间变量有关的系数矩阵.

本文所采用MPC主要包括模型预测、滚动优化和反馈校正3个过程.

预测模型能反映整个被控系统运行的真实状态，可为滚动优化及反馈校正过程提供参考，包括非参数化^{[11, 26-32]}和参数化模型2种. 本文采用基于参数化的HST状态空间模型，以设计参数为状态变量，通过改变参数值来构建并更新模型，基本过程如下：

对于HST单输入单输出调速系统，其状态空间方程的连续性模型为：

离散化后，可得，

式中：x(k)为n维状态变量(n为中间变量个数)；A_d，B_d和C_d为n×n，n×1和1×n维矩阵.

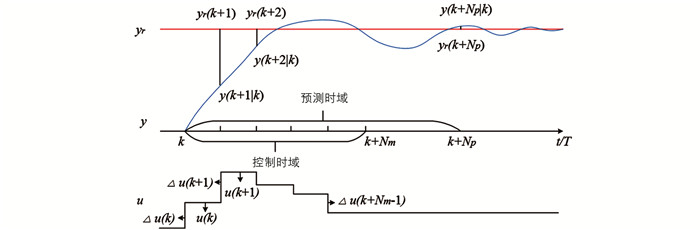
假设系统的预测时域为N_p，控制时域为N_m，则k时刻预测时域N_p(N_p＞N_m)内的状态变量的预测值为：

被控系统的预测输出值为：

联立式(9)和(10)，可推得预测时域内被控系统输出预测值的通用公式为：

式中：

G为N_P×N_m维矩阵.

新的状态空间模型通过k+1时刻和k时刻的状态变量和输出值式(8)求差得到，相应模型表示为：

式中：$ \boldsymbol{x}_{\boldsymbol{u}}(k)=\left[\begin{array}{c} \Delta \boldsymbol{x}(k) \\ y(k) \end{array}\right], \boldsymbol{A}_{\boldsymbol{u}}=\left[\begin{array}{cc} \boldsymbol{A}_{\boldsymbol{d}} & \boldsymbol{o}_{\boldsymbol{d}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{d}} \boldsymbol{A}_{\boldsymbol{d}} & 1 \end{array}\right], \boldsymbol{B}_{\boldsymbol{u}}=\left[\begin{array}{c} \boldsymbol{B}_{\boldsymbol{d}} \\ \boldsymbol{C}_{\boldsymbol{d}} \boldsymbol{B}_{\boldsymbol{d}} \end{array}\right], \quad \boldsymbol{C}_{\boldsymbol{u}}=\left[\begin{array}{ll} \boldsymbol{o}_{\boldsymbol{d}} & 1 \end{array}\right]$；o_d为与Δx相同维度的零向量，$\boldsymbol{\varDelta x}(k)=\boldsymbol{A}_{\boldsymbol{d}} \boldsymbol{\varDelta} \boldsymbol{x}(k-1)+\boldsymbol{B}_{\boldsymbol{d}} \Delta u(k-1) $.

MPC是一种局部优化的控制算法，其优化策略如图 2. 区别于全局优化算法，它在每一时刻k就要确定从该时刻起的N_m个控制增量Δu(k)，Δu(k+1)，…，Δu(k+N_m-1)，使得预测模型在未来N_p个时刻的输出预测值尽可能接近期望值.

MPC的性能优化指标函数为：

式中：Y_r为期望值矩阵(维数和Y相同)；R为控制权重矩阵(N_p纬度的单位向量)；$\boldsymbol{R}_\boldsymbol{s}^{\mathrm{T}}= \overbrace{\left[\begin{array}{llll} 1 & 1 & \cdots & 1 \end{array}\right]}^{N_p} y_r(k)=\overline{\boldsymbol{R}}_\boldsymbol{s}^{\mathrm{T}} y_r(k)$，为误差权重矩阵.

将式(11)带入式(13)中可得：

令J_e对ΔU的偏导最小，获得最佳控制增量：

此外，基于式(12)和式(15)，被控系统在k+1时刻的状态预测值表示为：

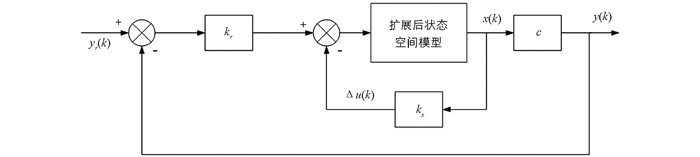
式中：K_s和K_r分别为$\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\boldsymbol{R}\right)^{-1} \boldsymbol{G}^{\mathrm{T}} \boldsymbol{F}{\boldsymbol{u}} $和$\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\boldsymbol{R}\right)^{-1} \boldsymbol{G}^{\mathrm{T}} \overline{\boldsymbol{R}}_{\boldsymbol{s}} $的首行元素，

鉴于矩阵F_u中C_uA_u的特殊结构，F_u最后1列的元素均为1，于是K_s可描述为K_s=[K_xK_r]·K_x即为与状态变量相关的反馈增益，K_r为与被控系统输出相关的反馈增益. 相应状态扩展的MPC控制框图如图 3.

由式(8)至式(16)可知，预测时域和控制时域(超参数)是影响MPC优化速度和精度的关键因素. 人工找寻最优的超参数会耗费大量的精力，而粒子群优化算法则可借助计算机自动找寻最优超参数，能有效提高计算效率. 本文采用粒子群优化算法对MPC中的预测时域和控制时域进行参数寻优.

所引入的粒子速度和位置更新公式为：

式中：v_i^d为第d次迭代时粒子i的速度；x_i^d为第d次迭代时粒子i的位移；w为惯性权重，调节收敛性；c₁，c₂为加速度常数，调节学习最大步长；r₁，r₂为随机数，增加搜索随机性；pbest_i为第i个粒子的最优位置；gbest为第i次迭代时整个粒子群内的最优位置.

为明确MPC系统性能是否达到最佳，本文选取2个参数作为最优目标，即控制系统的超调量和系统达到稳定的时间. 综合优化指标为：

式中：a₁，a₂为比重(a₁+a₂=1)；f₁，f₂为系统超调量和系统达到稳定的时间.

模型的预测输出与系统的真实输出会存在误差，为了提高模型的精确性，需要引入反馈进行误差校正. 相应的校正公式为：

式中：$\tilde{y} $为k+1时刻被控系统的真实输出；y_cor为k+1时刻反馈校正后的预测值矩阵；h为校正向量矩阵，维数为N_P.

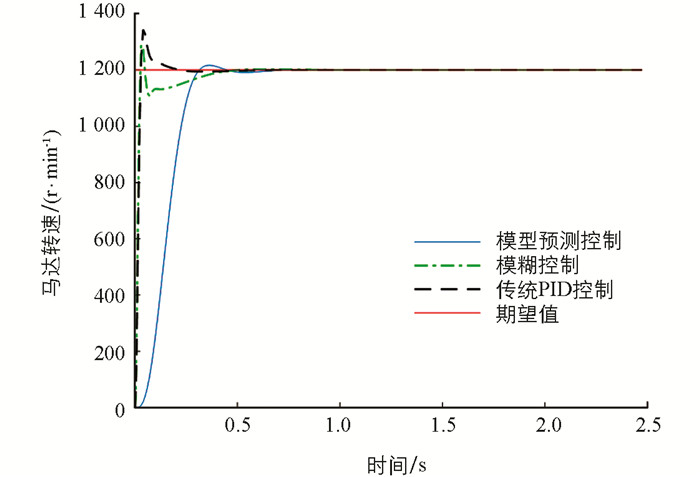
为验证MPC对HST的转速控制优势，本文对比研究了传统PID控制、模糊控制以及MPC对HST马达输出转速的影响，相应的仿真结果如图 4. 从图 4可以看出，3种控制方法均能在0.69 s左右使马达转速稳定在设定值：传统PID控制的响应速度最快，但超调量也最大，为11.92%；模糊控制的响应速度次之，超调量为7.42%；模型预测控制(MPC)的响应速度虽相对较慢，但其超调量最小，为1.42%，且振荡周期最短. 仿真结果表明，与传统PID控制和模糊控制结果相比，MPC的响应虽相对较慢但无多余扰动，可极大增强系统的安全性，具有潜在优势.

为验证模型预测控制策略对HST转速控制效果及其可行性，本文搭建了静液压传动实验平台(图 5). 该平台使用STM32F407ZGT6作为控制系统的主控芯片，动力装置选用可变频的三相异步电动机，传动装置选用贵州中航力源液压股份有限公司生产的LY-HPVMF-23-L-02C型静液压变速器，反馈装置和控制装置则通过霍尔式转速传感器、绝对值编码器和步进电机实现，主要参数如表 1. 基于该静液压传动实验平台，本文采用仿真和台架实验对比研究了MPC对HST的转速控制效果，即空载启动、转速阶跃响应和加减速状态复杂工况下的工作性能.

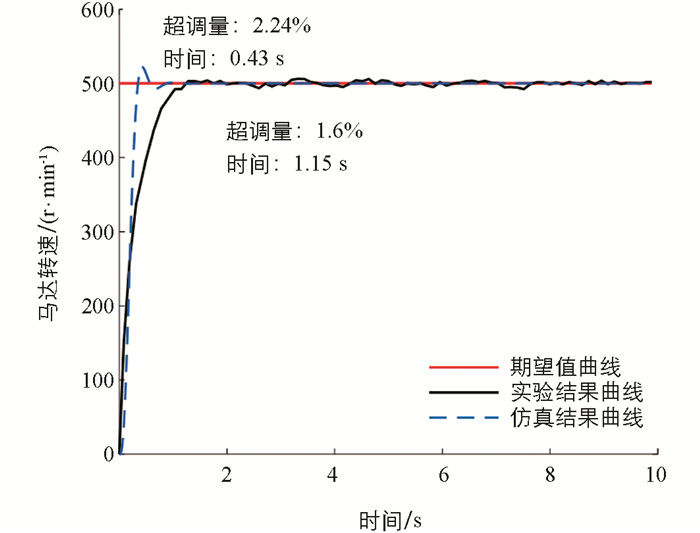
采用仿真和台架实验对比研究了HST系统从空载启动到期望转速过程中MPC的控制效果. 基于Matlab环境建立HST的状态空间模型和MPC控制系统，在预测时域N_p为28和控制时域N_m为12的最佳超参数下，系统从空载启动到期望转速为500 r/min的过程中，马达输出转速曲线如图 6.

从图 6的仿真结果曲线可以看出，MPC能在短时间内使HST的马达输出转速迅速提高，系统的超调量为2.24%(时间为0.43 s)，且系统在1.03 s时达到稳定状态. 调控过程中，通过滚动优化可以使HST的马达输出转速快速增加，并以较小的转速波动达到稳定状态. 与仿真结果相比，台架实验所得HST的马达输出转速增长较为缓慢，在启动后1.15 s时达到500 r/min的期望值，系统超调量为1.6%；在2.11 s时马达输出转速达到相对稳定状态，并在期望转速附近波动，波动范围小于1.6%. 对比分析结果可知，MPC控制HST的台架实验结果和仿真结果一致，MPC能使马达转速快速平稳地增长，系统以较小的超调量达到稳定状态，并能抑制系统稳态时的转速波动，提高系统的静动态特性.

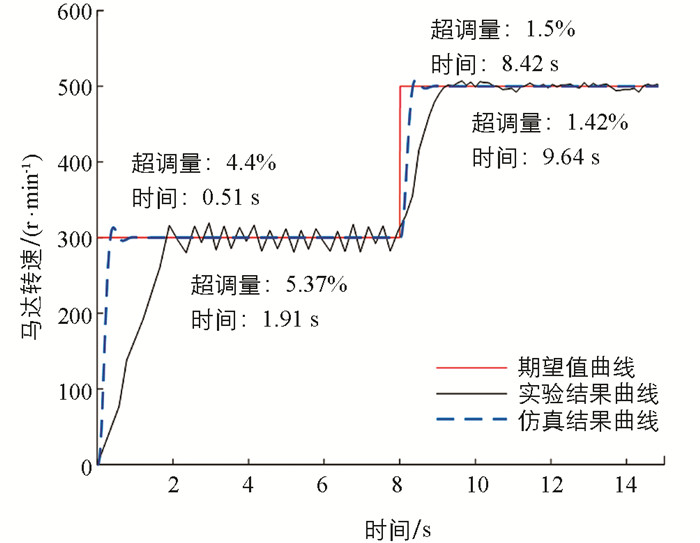
为验证MPC对HST的控制效果，本文进一步研究了马达转速突变工况下，基于MPC的HST对期望转速的跟踪能力. 实验中设置电动机以1 200 r/min的转速恒定输出，HST启动时的期望转速为300 r/min，在HST工作8 s后使期望转速突增为500 r/min. 图 7为期望转速增加下的HST马达输出转速曲线.

从图 7的仿真结果曲线可以看出，MPC具有良好的控制性能，启动时超调量为4.4%(时间为0.51 s)，马达转速在1.17 s达到稳定状态，使系统在转速稳定阶段有较好的静态特性；期望转速突增后，控制系统亦具有较好的动态特性，即变换过程迅速且无明显波动，在9.13 s使系统重新达到新的稳定状态. 相比仿真结果，台架实验中马达输出转速于1.91 s在300 r/min的期望转速附近周期性波动，系统超调量为5.37%；而在转速突增阶段，HST的马达转速在1.64 s内即可平稳快速地达到期望值500 r/min，超调量降低为1.42%. 从图 7还可以看出，实验结果曲线在低转速阶段比高转速阶段的马达输出转速波动大，其原因在于HST在较低转速下工作时，对应的变量泵的斜盘只有很小的调节范围，与较高的工作转速相比，步进电机在相同的歩距角下调节斜盘所产生的转速变化更大.

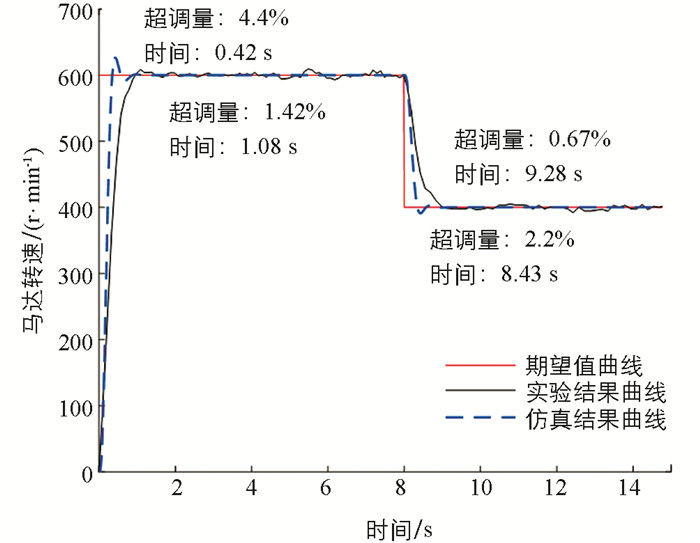
由图 8中的仿真结果曲线可知，HST在1.15 s内使马达输出转速从零达到期望值600 r/min并稳定；当期望转速突降为400 r/min时，马达输出转速亦能在调整后的1.13 s内快速达到设定值并进入新的稳定状态. 在台架实验中，HST无论在启动还是减速阶段，MPC都能使HST快速做出响应，减小系统的超调量，使马达转速平稳迅速地达到设定值. 在系统的稳定工作阶段，MPC亦能有效抑制马达转速波动，提高系统的静态特性.

以上研究结果表明，在阶跃响应和加减速工况下，实验结果与仿真结果一致，表明MPC可对HST转速进行有效控制，其不但能提高系统的静动态特性，使系统具有良好的自适应能力，还能抑制调控过程中产生的转速波动，增强系统的鲁棒性.

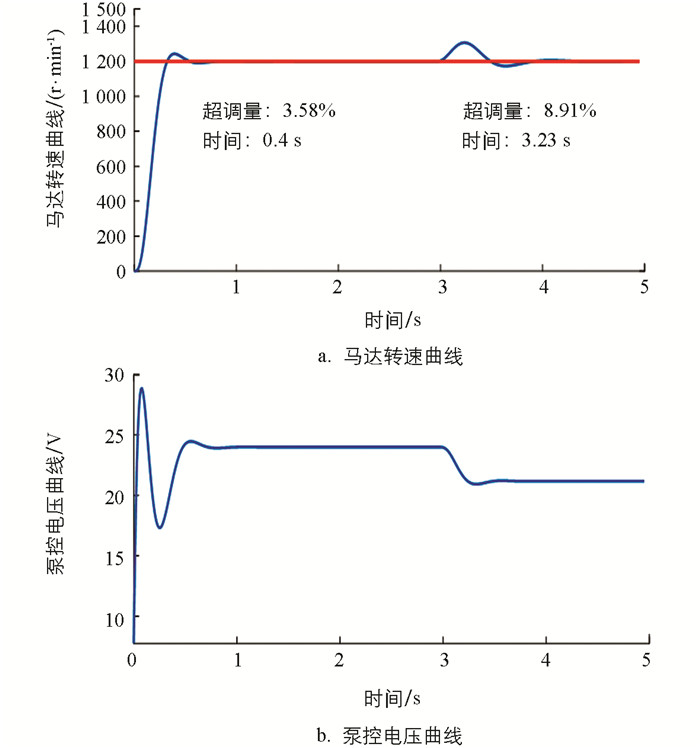
基于以上的对比验证，本文进一步研究了复杂工况下MPC对HST输出转速的控制性能，即变化的输入功率、多变的期望转速和突变的外部负载. 当遇到大负载时，即HST的输入功率增大的工况下，研究MPC对HST马达输出转速稳定性的影响. HST以1 500 r/min的输入转速启动，相应的转速突变仿真结果如图 9.

从图 9中可以看出，系统能在1 200 r/min的期望转速下稳定工作. 在3 s时，输入转速增加到1 700 r/min，系统仍然能在1 200 r/min的期望转速下运行. 由式(5)可知，随着输入转速(与输入功率成正比)的增大，相同泵排量下的马达转速也随之增大. 为维持不变的马达转速，控制器应减小泵的排量，以满足在负载突变的情况下转速恒定的要求. 研究结果表明，MPC控制器在HST的输入功率增大时，能在短时间内以较小的转速波动使马达转速稳定不变，降低对输出转速造成的影响.

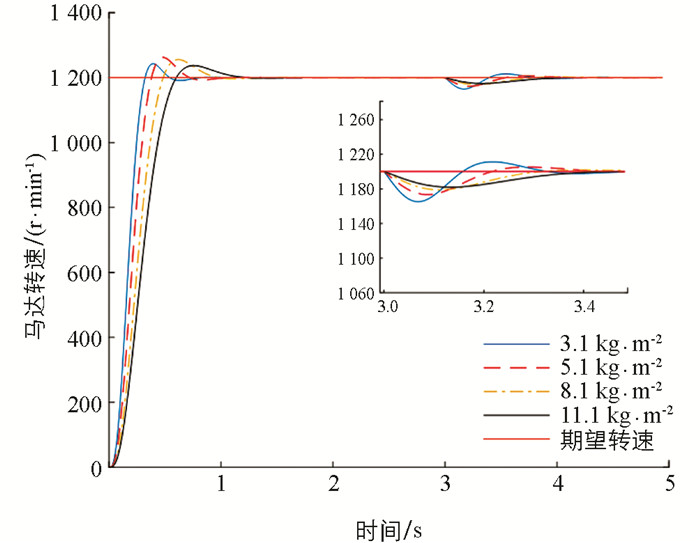
为验证系统的抗干扰能力，将外部负载作为干扰加入到系统中. 考虑到实际工作中的外部负载是通过车轮传递给HST输出轴，会受到车轮和HST输出轴的轴径影响^[33]. 本文引入负载T_l与等效转动惯量J综合描述外部负载，作为系统的干扰项d=T_l/J. 图 10是在等效转动惯量分别为3.1，5.1，8.1，11.1 kg/m²时马达输出转速曲线，不同干扰下的系统性能指标见表 2. 从图 10可以看出，等效转动惯量对系统的响应速度、超调量、稳定时间都有一定的影响，且等效转动惯量越大，控制系统的静态性能越差. 由式(4)可知，HST的等效转动惯量越大，其输出轴的转动力矩也就越大，马达进出口的压差变大，相同转速下所需泵的排量也就增大，因此，控制马达加速的时间变长. 在系统稳定工作3 s后，将HST的外部负载由0增加为50 N·m，此时，等效转动惯量越大的马达转速波动反而越小. 出现该现象的原因在于相同的负载条件下，转动惯量越大，干扰越小，对系统造成的影响也就越小. 该数值结果与理论分析一致，表明当系统遇到干扰时，MPC仍能使马达转速较好地跟踪设定值，快速达到稳定，使系统具有良好的鲁棒性.

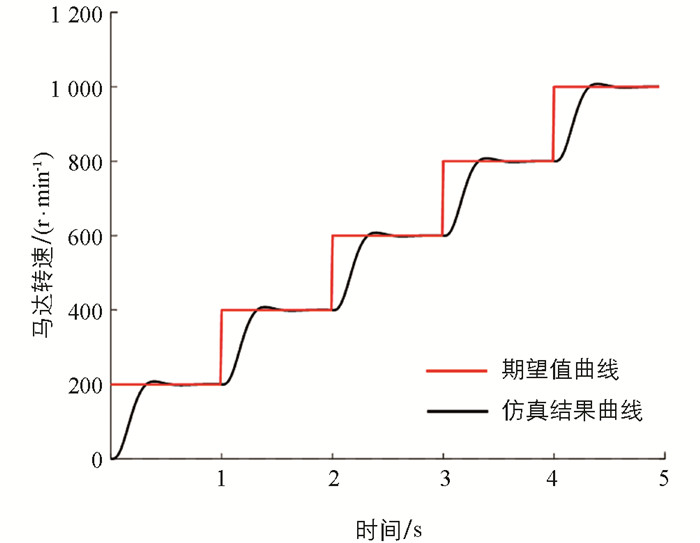
在HST工作的5 s内，设置马达的期望转速以200 r/min的步长，由零逐步增加到1 000 r/min，研究得到HST的马达输出转速追踪曲线(图 11). 由图 11可知，无论在低转速还是高转速下，MPC都能使HST的马达输出转速平稳地跟随期望值，并在1 s内完成调控过程，使系统达到稳定状态. 研究结果表明，对于变化频繁的工作转速要求，MPC能快速调节变量泵的排量，使HST以较小超调量完成转速变化过程.

本文引入模型预测控制(MPC)算法对HST的转速控制进行仿真和实验研究. 首先基于扩展后的状态空间方程建立了HST的数学模型，并采用粒子群优化算法(PSO)对MPC中的预测时域和控制时域进行参数寻优，得到综合性能指标最佳的MPC控制器模型；然后结合仿真和台架实验验证MPC对HST控制的有效性；最后研究了复杂工况下MPC对HST的控制性能. 主要研究结果如下：

1) 采用仿真与台架实验研究得到的MPC对HST转速控制效果一致. 结果表明，在不同阶跃转速下启动时，MPC控制的HST都能以较小的超调量快速地达到期望转速，并以较小的转速波动进入稳定状态；针对马达输出转速突变的工况，MPC能快速响应，调控过程准确且迅速，使HST能在短时间内重新进入新的稳定状态.

2) 复杂工况下的仿真研究结果表明，MPC能在原动机的输入功率变化时保持HST的输出转速恒定不变；能在负载突变时稳定HST的输出转速，抑制因负载变化而产生的转速波动，增强系统的鲁棒性；MPC能在不同的期望转速下使HST的马达输出转速平稳地跟随期望值，使系统具有良好的静动态特性.