-
开放科学(资源服务)标识码(OSID):

-
松茸是一种天然名贵的食药两用菌类,因其营养丰富、味道鲜美,历来被誉为“菌中之王”[1],由于它含有丰富的氨基酸和多种人体必需的矿物质,还存在具有保健作用的活性成分,因此具有降血脂、抗氧化、抗癌、改善心血管疾病等保健功能[2-3],还可起到提高免疫力和美白的作用[4]. 姬松茸原产于巴西,后传入我国,它同样具有良好的食药两用营养价值,也富含多种活性成分[5],具有增强免疫、抗氧化、抗突变和抗疲劳等功效[6],而且抗癌效果明显,故被广泛应用于癌症和白血病等疾病的辅助治疗[7]. 正是由于松茸与姬松茸具备的药食两用功效,近年来受到国内外营养学家及药学研究工作者的广泛关注. 魏晓梅等[8]研究了松茸多糖的提取方法及测定;申秀娟等[9]则利用酵解姬松茸中的提取物,开展了姬松茸多糖对小鼠免疫和肠道菌群影响的研究;石芳等[10]开展了采用不同的干燥方式,对松茸的营养成分、氨基酸及挥发性成分影响的研究;Zhai等[11]就松茸含有的赖氨酸等营养及抗氧化成分对人体作用展开了研究;此外还有一些侧重松茸活性酶有关性质的研究[12-13],以及松茸挥发性成分的检测分析[14]. 所有的这些研究虽然较多,但普遍都是单纯通过实验进行的研究,耗时长、过程复杂. 先理论研究再指导实验已成为科学研究中一种简便而高效的方法,这一方法应用于松茸和姬松茸的研究目前还较为少见[15]. 近年来人工神经网络(Artificial neural network)方法在众多领域得到广泛应用[16-20],本文采用人工神经网络法中常用的BP算法[21-22],对文献[23]所列松茸和姬松茸145种挥发性成分(其中1个分子重复,实际144个分子),通过定义一种新的分子结构指数(原子指数A),结合电性拓扑状态指数、电性距离矢量与色谱保留时间进行构效关系(QSRR)分析,构建了BP神经网络模型,预测所得保留时间与文献实验值较为吻合. 利用该神经网络模型可快速获取挥发性成分的保留值,研究结果对提高定性分析能力、探索色谱保留机制具有积极的意义.
全文HTML
-
松茸和姬松茸挥发性成分及色谱保留时间来源于张宪臣等[23]的分析测试结果,其中松茸包含了酯类、酸类等9类76种挥发性成分(表 1),姬松茸包含了醛类、醇类等9类68种挥发性成分(表 2).
-
不同原子因电子层数、价电子数、电负性等性质及连接的氢原子数有所不同,故导致构成分子的特性也各不相同. 通过考察文献[23]中76种松茸和68种姬松茸挥发性成分的保留时间与其分子结构之间的关系,新定义一种用于表征原子特性的特征值(Ti)为:
式中:mi,χi分别为原子i的价电子数、鲍林电负性;χc为碳原子鲍林电负性;hi为与i原子直接连接的氢原子数,如基团=O,按式(1)计算氧原子To为4.797;如基团—OH,则氧原子To为3.997. 在邻接矩阵基础上,建构化合物新的分子结构参数—原子指数A为:
式中:∑表示每一个非氢原子对分子的贡献加和,由于考虑的是每个原子对分子的贡献,故将其命名为原子指数,76种松茸和68种姬松茸挥发性分子的原子指数A分别列于表 1和表 2中.
-
根据文献[23]所列的76种松茸和68种姬松茸挥发性成分分子,先用建构的原子指数A与这些分子的色谱保留时间进行回归分析,对松茸所得一元方程的相关系数为0.845,对姬松茸所得一元方程的相关系数为0.902,基本能达到回归分析要求,但并不理想. 考虑到这些挥发性分子的类型比较复杂,只用一种指数显然不能满足准确预测的要求,为此使用文献[24]的方法自编程序,计算这144个分子的电性拓扑状态指数和电性距离矢量,结合建构的原子指数A,先对松茸挥发性成分的色谱保留时间进行回归分析,优化筛选出电性拓扑状态指数的E2和电性距离矢量的M15和M21进行回归分析(表 1),建立的四元线性方程为:
式中:n为分子样本数;r,radj2,S,F分别为所建模型的相关系数、调整的可决系数、标准误差、Fischer检验值,可以得出四元回归模型的相关系数为0.883,根据该模型计算得到的保留时间见表 1中预测值1.
同理用该4种参数对姬松茸挥发性成分的色谱保留时间进行回归分析(表 2),建立的四元线性方程为:
可以得出四元回归模型的相关系数为0.916,根据该模型计算得到的保留时间见表 2中预测值1. 不难看出,根据多元回归分析方程式(3)和式(4)得到的预测值与实验值还存在较大的误差.
-
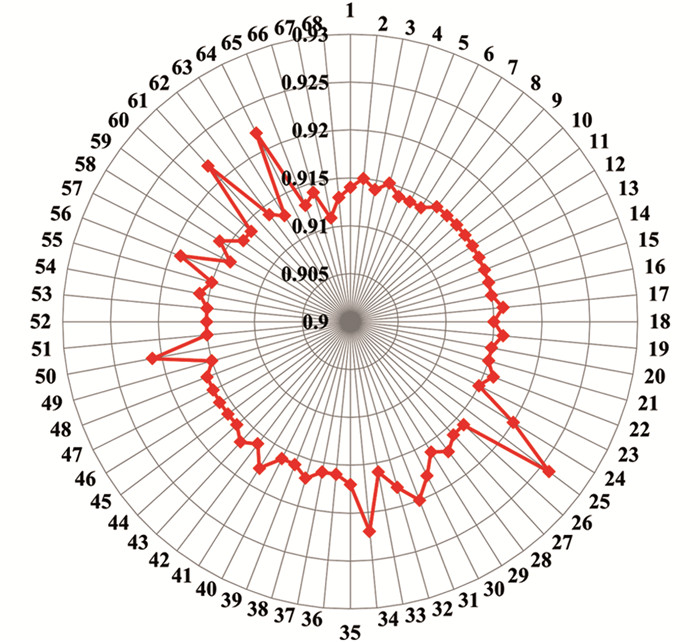
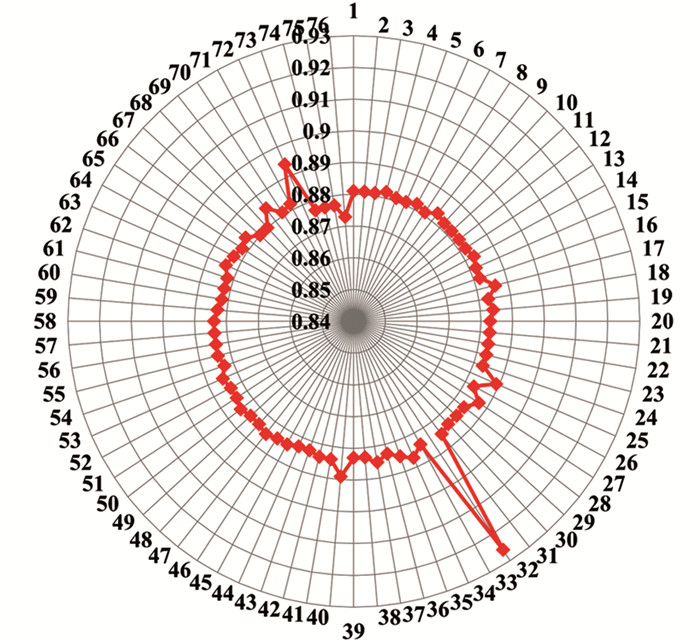
为检验选用的分子结构参数作为神经网络模型变量的可靠性,用逐一剔除法对选择的4个结构参数所建的2个方程稳健性进行检验. 先对式(3)每次剔除1个分子,用余下的分子进行建模,这样共得到76个相关系数检验值. 对这76个检验值作雷达图(图 1),可以看到,只有剔除第32号十四碳烯酸分子时,所得方程的相关系数值最大,说明该分子的存在对总体相关性影响较大. 这可能与该分子链较长而保留时间相对较小有关,但总体而言,检验相关系数所得r的平均值为0.883 6,与多元回归分析所得式(3)的相关系数值基本吻合,说明采用这4个变量来构建相关性模型稳健性可靠. 同理,对式(4)用相同的方法进行检验,得到68个检验的相关系数. 对这68个检验值作雷达图(图 2),检验相关系数所得r的平均值为0.916,与多元回归分析所得式(4)的相关系数值完全一致,说明采用这4个变量来构建姬松茸挥发性成分保留时间的相关性模型同样稳健可靠.
1.1. 数据来源
1.2. 原子指数A的定义与建构
1.3. 电性拓扑状态指数及电性距离矢量的计算及回归分析
1.4. 模型稳健性检验
-
由于多元回归方程的相关性不够理想,为提高预测能力,在多元回归方程基础上进一步用神经网络法进行研究. 按照许禄等[25]及Andrea等[26]的建议,神经网络隐含层变量(Y)可按式(5)计算:
式中:n,Si,Y,So分别为神经网络的分子样本数、输入层、隐含层和输出层变量.
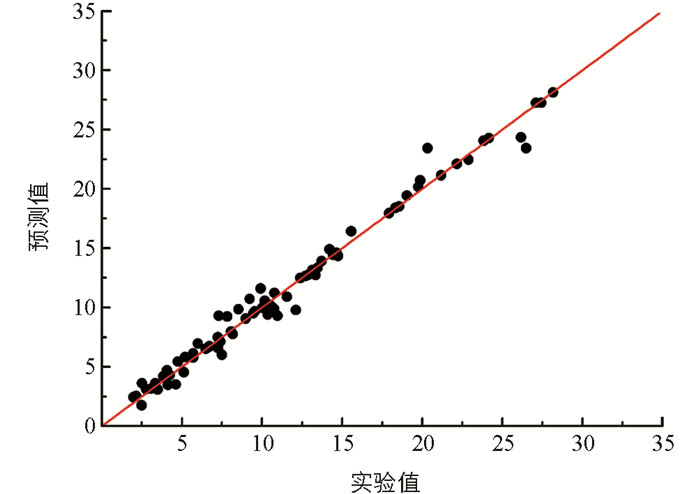
将松茸挥发性成分的A,E2,M15和M21 4个分子结构参数作输入层变量,色谱保留时间作输出层变量,根据隐含层计算公式,隐含层Y可取6,7或8,经过计算分析比较,发现当Y取8时,所得结果最好,故对松茸挥发性成分色谱保留时间预测的神经网络结构方式采用4-8-1. 为防止建模过程中的过拟合,将76个分子分为3组:第1组为训练集组(以每5个分子为1组,取其中第1,3,5个分子)、第2组为测试集组(每5个分子组中的第2个分子)、第3组为验证集组(每5个分子组中的第4个分子). 通过建模计算,得到了松茸挥发性成分色谱保留时间预测模型各组集相关系数值为r总=0.991 9,r训练集=0.991 0,r测试集=0.993 2,r验证集=0.997 4. 与多元回归方程(3)相比,神经网络模型相关系数明显提高,预测的松茸挥发性成分的色谱保留时间与文献实验值的吻合度较好,两者的平均误差仅为0.57. 将神经网络模型所得的预测值2、实验值以及两者之间的误差列于表 1中,其关系见图 3.
-
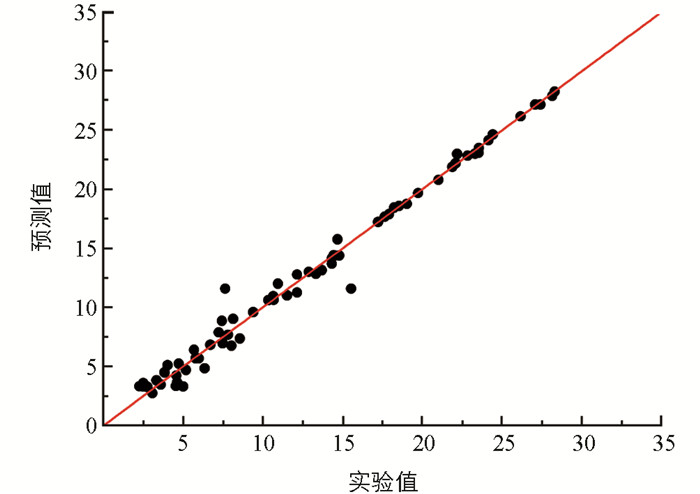
将姬松茸挥发性成分的A,E2,M15和M21 4个分子参数作为输入层变量,相应色谱保留时间作为输出层变量,根据隐含层计算公式,Y可取5,6或7,经计算分析当Y取7时,所得的结果较好,故对姬松茸挥发性成分色谱保留时间预测的神经网络结构方式采用4-7-1. 模型的各个组集相关系数分别为r总=0.992 9,r训练集=0.990 5,r测试集=0.997 1,r验证集=0.996 3. 利用该神经网络模型预测的姬松茸挥发性成分的色谱保留时间与文献实验值的平均误差为0.58,将相关分子的预测值2与实验值列入表 2,其关系见图 4. 结果表明:无论是松茸还是姬松茸,根据模型所得预测值与实验值对应的点均在直线附近,说明没有误差特别大的数据存在.
-
为检验所建构模型的可靠性,以建构的姬松茸神经网络模型为例,对姬松茸中其他挥发性成分的保留时间进行检验,这里的姬松茸分子及相关数据随机选取于文献[27]中的分子,用模型对这些分子的保留时间进行预测,可以看到预测值与实验值基本相符(表 3),说明本法建构的模型基本可靠.
2.1. 松茸神经网络模型建构
2.2. 姬松茸神经网络模型的建构
2.3. 建构模型的检验
-
不同产地松茸和姬松茸中各种成分或含量均会存在一定的差异,而且这些挥发性成分种类较多,组成复杂,一般采用实验方法对其进行检测分析过程漫长而繁琐. 本法通过建构一种新的原子指数A,结合计算松茸和姬松茸挥发性成分的电性拓扑状态指数和电性距离矢量,并优化筛选了其中的几种结构参数,采用反向传播(BP)神经网络方法建构预测模型. 建构的原子指数充分考虑了分子中原子本身的电性以及所处环境的空间结构特性,从而蕴含了对分子的贡献;选择的电性拓扑状态指数和电性距离矢量则同样能反映电性结构信息和空间拓扑结构连接性质. 将他们结合可以充分反映松茸或姬松茸挥发性成分保留时间的变化规律,从表 1和表 2中松茸和姬松茸挥发性成分的结构参数和保留时间的大小可以看出,当检测条件一定时,除原子之间的范德华力、色散力、诱导力等会影响保留时间外,基团的大小、数量甚至连接情况均能影响保留时间的大小. 在对所建模型的稳健性检验中可以看到,当剔除32号分子十四碳烯酸时,模型检验的相关系数相对明显高于其他值,说明长链的存在,由于体积越大,对保留时间影响也越大. 本文建构一种新的原子指数A,结合E2,M15和M21共4种结构参数,与松茸和姬松茸挥发性成分的色谱保留时间构建BP神经网络模型,模型总相关系数能达到0.99以上的优级相关,预测松茸保留时间与实验值的平均误差为0.57,预测姬松茸的平均误差为0.58,说明本法具有较好的可靠性,所建模型的预测能力较强,预测准确度较好.
新建构的原子指数A、筛选的电性拓扑状态指数的E2和电性距离矢量M15,M21,它们能充分反映松茸和姬松茸挥发性成分中非氢原子的数量和连接特性. 通过分析挥发性成分的分子结构发现,基团—CH3,—CH2—和含有的杂原子(如氧原子、氮原子)是影响保留时间大小的一个主要片段,原子上连接的氢原子数量多少也会对性质有影响. 从神经网络模型的相关系数明显高于多元回归模型可以看出,4种分子结构参数与松茸、姬松茸挥发性成分色谱保留时间之间存在较好的非线性关系,与多元回归中反映出的线性关系不同. 建构的松茸与姬松茸色谱保留神经网络模型,预测能力明显优于多元回归分析法,所得结果较为理想.



 下载:
下载: