-
开放科学(资源服务)标识码(OSID):

-
电池管理系统(Battery Management System,BMS)对于电动汽车和电池储能系统的安全性和可靠性至关重要. 电池荷电状态(State of Charge,SOC)估计是BMS的基础[1-2],为了实现锂离子动力电池SOC的准确估计,国内外学者在该领域开展了大量研究工作.
当前绝大多数研究采用基于模型的方法,常见的可分为基于电化学模型、神经网络模型和等效电路模型[3]3种方法. 电化学模型依托多孔电极和浓溶液理论,运用数学方法详尽阐述电池内化学反应与电极动态,从电化学反应机理中分析问题,能够深入了解电池的电化学机制. 但由于其模型结构复杂,建模时需要强大的计算能力和较多的数据[4-5]. 神经网络模型通过收集锂离子动力电池大量历史数据,包括电流、电压、温度等信息,能够在不了解电池工作原理的情况下构建数据与SOC之间复杂的线性关系[6-8],最终得到电池SOC预测数据. 然而当训练数据减少、网络参数设置不当时,该方法估计精度会变差,估计结果波动会变大[9]. 等效电路模型通过模拟电子元件的输入输出行为来捕捉锂离子动力电池的动态特性,主要有Rint模型[10]、PNGV模型[11]和Thevenin模型[12]等. 等效电路模型通常结合滤波算法建立状态空间方程估计电池SOC,该方法具有复杂度低且精度较高等优点,可适用于不同类型的电池,因此一般采用等效电路模型应用于实际SOC的估计[13].
电池动态参数的准确识别是保证锂离子动力电池系统安全、可靠运行的前提. 目前,常用的参数辨识方法是离线HPPC法. 在建模过程中,由于检测量伴随着不确定的噪声信号,离线辨识不仅耗时长,而且结果不准确. 如果采用在线方法进行参数辨识,则可以实时补偿噪声产生的误差. 周坤等[14]提出了一种扩展卡尔曼滤波(EKF)自适应无迹卡尔曼滤波(AUKF)联合算法在线估计电池模型参数与SOC,通过在不同工况下的试验数据进行验证,该方法能够实现电池参数和SOC实时估计. 但EKF算法在线性化过程中引入了导数计算,此计算过程中忽略了高阶项引起的截断误差,因此降低了SOC估计精度. 为解决卡尔曼滤波在非线性状态转换为线性状态过程中出现的误差问题,Wang等[15]提出一种双无迹卡尔曼滤波(DUKF)算法,在考虑电化学极化和浓度极化的双极化(DP)模型基础上,在线实现参数辨识和SOC估计. 该算法考虑了参数的实时变化,对运行过程中的噪声信号进行补偿,避免了实际环境中环境因素的影响,因此该方法的精度和效率优于EKF算法. 在实现上述算法时,过程噪声协方差Pk和观测噪声协方差Rk通常是已知且平稳的. 由于假设变量的分布为高斯分布,当噪声协方差为具有已知统计量的高斯时,估计过程可以很好地执行. 然而,在非高斯分布的情况下,过程和观测噪声序列的统计量是未知的. 为此,研究人员开发了基于变分贝叶斯(Variational Bayesian,VB)[16]的噪声估计算法,该方法利用逆Wishart分布和VB方法来推断Pk和Rk.
为解决过程噪声和观测噪声时变会降低滤波精度这一问题从而提高锂离子动力电池SOC的估计精度,本文提出一种无迹卡尔曼滤波和基于变分贝叶斯自适应时变噪声无迹卡尔曼滤波的参数和SOC联合估计方法(UKF-VBAUKF),具体方案为:①首先建立二阶等效电路模型,采用无迹卡尔曼滤波辨识模型参数;②其次利用逆Wishart分布对Pk和Rk进行建模,对Pk进行迭代更新来降低过程噪声的影响,对Rk进行迭代更新降低观测噪声的影响;③最后采用UKF-VBAUKF算法实现对电池状态Xk、Pk和Rk的联合估计,从而提高锂离子动力电池SOC的估计精度.
全文HTML
-
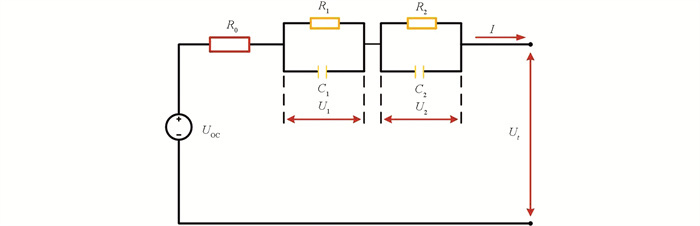
电池模型的建立是SOC估计的基础,它不仅需要反映电池的静态和动态特性,并且要易于实现. 考虑到模型精度和复杂度成正比,本文选用如图 1所示的无迟滞的二阶等效电路模型. 该模型结构简单,物理意义清晰,足以模拟电池的静动态性能,同时也便于电池特性分析和参数辨识[17]. 其中R0为电池的欧姆内阻;由R1、R2、C1、C2组成的2个RC网络代表电池的极化电阻和极化电容;U1和U2为电池的极化电压;Ut为电池端电压;UOC为开路电压(Open Circuit Voltage,OCV);I为电池的负载电流.
基于基尔霍夫电压和电流定律得到二阶等效电路模型的状态空间表达式(1)和观测方程(2):
其中:R1、R2、C1、C2分别为电池的极化电阻和极化电容;UOC为电池OCV;U1、U2为极化电压;Tx为采样时间;Qn为电池容量;R0为电池欧姆内阻;I为电池负载电流;SSOC为电池的SOC值. 为了便于计算机处理,需将式(1)、式(2)进行离散化处理,得到二阶RC模型的线性离散化方程如式(3)所示:
-
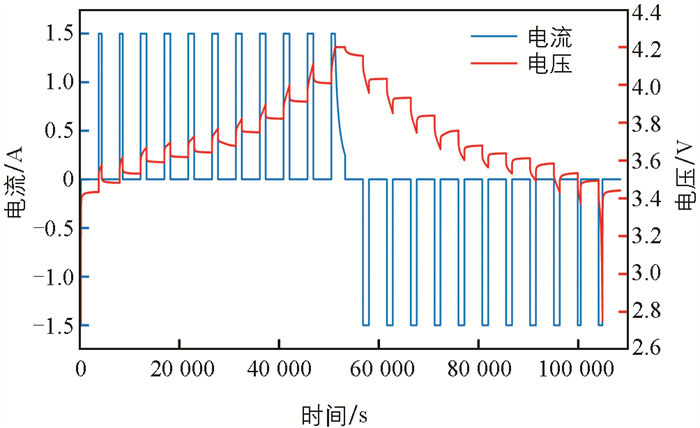
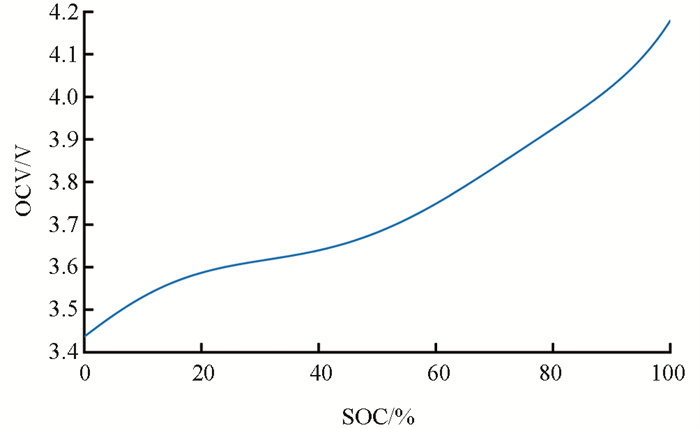
测试采用额定电压.6 V,标称容量为5 000 mAh的NCR26650锂电池作为试验对象,采用美国Arbin公司生产的LBT系列5 V/30 A电池充放电测试仪作为电池试验平台. OCV测试试验具体步骤如下:采用0.3 C电流倍率对电池进行恒流放电,当电池端电压下降到下截止电压时,静置1 h使电池内部反应达到稳态,记录当前端电压值. 依据容量测试试验获得电池最大可用容量,使用0.3 C电流倍率进行恒流恒压充电,以充入电池的容量为截止条件,每充入10%的最大可用容量后静置1 h,记录当前端电压值,直至电池容量充满. 静置1 h,同样采用0.3 C的电流倍率对电池进行放电,每放出10%的最大可用容量后静置1 h,记录当前端电压值,与每阶段的SOC相对应,OCV测试结果如图 2所示. 进一步对数据进行多项式拟合,通过式(4)对OCV与SOC的数据点进行六阶拟合,得到OCV与SOC的函数对应关系,OCV-SOC曲线如图 3所示.
式中:pi(i=1,2,…,7)为多项式拟合系数.
-
为使所建立的模型实现电池端电压预测,需要对电池内部参数进行辨识. 参数辨识方法可分为离线参数辨识和在线参数辨识,离线辨识的模型参数固定,不适用于复杂工况[18]. 电池模型中的参数R1、R2、C1、C2和R0会随着电池SOC的变化而动态调整,所以本文采用UKF算法在线辨识参数,这一算法能够实时地、自适应地更新电池模型中的这些参数,以反映电池状态随时间的变化,从而确保SOC的估计结果更加精确. 为了便于分析,使用式(5)表示非线性离散系统:
式中:k表示时刻;θ =[R0 R1 C1 R2 C2]T;ω k,vk为系统的过程噪声和观测噪声;ρk为模型参数过程噪声;x为n维系统状态向量;y为m维系统输出向量.
UKF在线参数辨识的具体算法执行流程[19]如下所示:
步骤1 初始化参数变量和协方差矩阵,确定UKF算法的参数. λ是一个调节参数,用来调节采样点到均值的距离,λ=α2(M+ki)-M,其中比例因子α=0.01,次级比例因子ki=0;M为模型阶数;β为非负权重系数,取值β=2.
步骤2 计算k时刻采样点.
步骤3 计算权重.
步骤4 计算参数预测值
$\overline{\boldsymbol{\theta}}_{k+1}$ 和系统方差预测值Pxx.步骤5 更新预测参数.
步骤6 更新观测值
$\hat{\boldsymbol{y}}_{k+1}$ 和观测方差预测值Pyy.步骤7 计算参数变量协方差Pxy、无迹卡尔曼增益K.
步骤8 观测更新.
步骤9 系统参数更新.
-
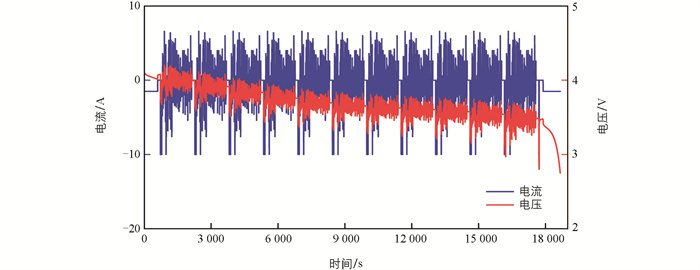
采用城市道路循环(Urban Dynamometer Driving Schedule,UDDS)工况作为在线参数辨识实际工况. UDDS是一种高功率测试工况,其特点是汽车加速和减速更为快速和激烈. 在UDDS工况下,电池电压变化很大,放电电流也相对较大. 这种工况模拟了一种对电池性能要求极高的驾驶环境,是评估在高功率需求下电池性能的重要手段. 电池在20 ℃时UDDS工况下的实测电压和实测电流如图 4所示.
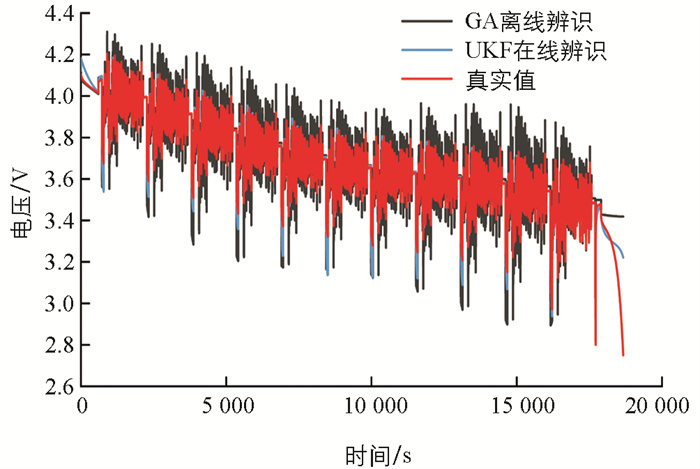
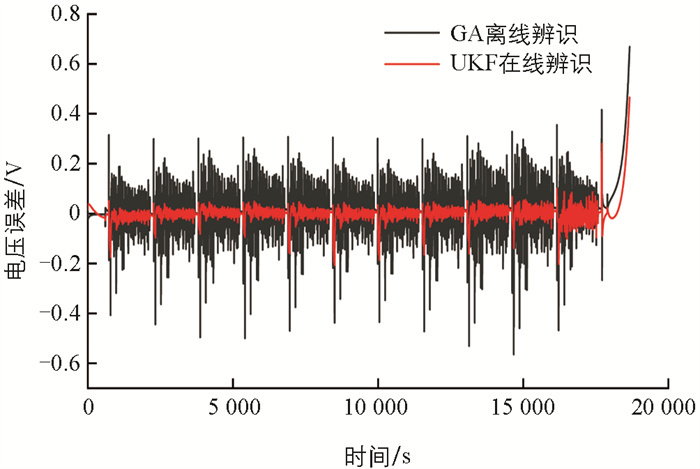
为了说明UKF算法在线参数辨识结果的准确性和可靠性,图 5显示了UDDS工况下端电压测量结果与估计结果的对比,图 6显示了2种辨识方法辨识出的端电压误差,其中黑线表示遗传算法(GA)离线辨识结果,红线表示UKF在线辨识结果. 由图 5可知,由GA离线辨识所得模型电压的平均绝对误差(MAE)为0.054 7,均方根误差(RMSE)为0.089 3;相比之下,采用UKF在线辨识所得模型电压的MAE降低至0.020 2,RMSE降低至0.042 1. 图 6显示在15 000 s后端电压误差逐渐增大,在最后时刻甚至超过400 mV,这主要是因为在低电量区间电池内部极化效应加剧的影响,但总体误差都分布在50 mV以内,这充分证明了通过UKF算法进行在线参数辨识所构建的电池模型,不仅具备高度的精确性,其误差波动范围也较小,展现出了良好的鲁棒性.
2.1. OCV-SOC曲线
2.2. 基于UKF算法的在线参数辨识
2.3. 模型参数结果验证
-
在现有的多种估计算法中,假设噪声协方差Pk和Rk服从高斯分布[20]. 高斯白噪声是一种功率谱密度均匀分布的随机变量噪声. 但实际应用中的噪声不可能是理想的高斯白噪声,噪声协方差随着时间变化而变化,因此本文引入VB方法对Pk和Rk进行估计以提高卡尔曼滤波器对Xk的估计精度.
在将VB方法的思想引入到UKF中时,该方法利用逆Wishart分布来推断和预测状态变量的观测噪声及其协方差矩阵. 具体来说,通过VB方法,可以建立一个模型,其中观测噪声的协方差矩阵被视为一个随机变量,并假定其先验分布遵循逆Wishart分布. 在UKF的迭代过程中,利用VB方法不断更新这一先验分布,结合观测数据来近似得到其后验分布,从而实现对观测噪声及其协方差矩阵的动态估计和预测. 这样,UKF在处理含有不确定性的观测噪声时,能够更加鲁棒和精确. 基于变分贝叶斯自适应时变无迹卡尔曼滤波算法(VBAUKF)的实现过程如下所示:
步骤1 初始化:设状态变量 X =[SSOC U1 U2]T,生成2n+ 1个sigma点,其中n=3.
步骤2 确定加权系数ωm,ωc.
步骤3 得到预测的sigma点集后,根据上一步计算得到的相应权重,通过加权求和的方式来估计和计算出系统状态的预测值
$\hat{\boldsymbol{X}}_{k+1 \mid k}$ 和协方差矩阵Pk+1|k.步骤4 根据预测值再次进行UT变换,得到新的sigma点.
步骤5 由新的sigma点计算预测的观测值
$\hat{\boldsymbol{Z}}_{k+1 \mid k}$ . 然后计算出自协方差 P zk|zk和交叉协方差Pxk|zk.UKF中的交叉协方差和自协方差可以理解为交叉协方差和自协方差的sigma点逼近. 根据变分原理和贝叶斯分析,迭代计算预测误差协方差矩阵Pk和观测噪声协方差矩阵Rk,迭代次数N根据实际情况选择. 在UKF算法中引入迭代的思想如下:
首先,设置初始迭代参数:
式中:
$\hat{t}_{k+1 \mid k}$ 和$\hat{\boldsymbol{T}}_{k+1 \mid k}$ 分别为协方差矩阵$\boldsymbol{P}_{k+1 \mid k}$ 的自由度参数和逆尺度矩阵;$\hat{u}_{k+1 \mid k}$ 和$\hat{\boldsymbol{U}}_{k+1 \mid k}$ 分别为协方差矩阵Rk+1|k的自由度参数和逆尺度矩阵;n为状态向量维数;m为观测维度;τ为Pk+1|k的调节参数;τ>0,ρ是$\hat{\boldsymbol{U}}_{k+1 \mid k}$ 的遗忘因子,ρ∈(0,1].然后,开始迭代,j=1,2,…,N.
计算预测误差协方差:
计算观测噪声协方差:
计算无迹卡尔曼增益:
计算预测误差协方差:
循环之后,输出参数为:
在每一次的采样周期结束后,所得到的预测状态值、预测误差协方差矩阵将作为下一次采样时执行时间更新(预测)和测量更新步骤的初始输入数据,从而实现滤波器对噪声的不断更新.
-
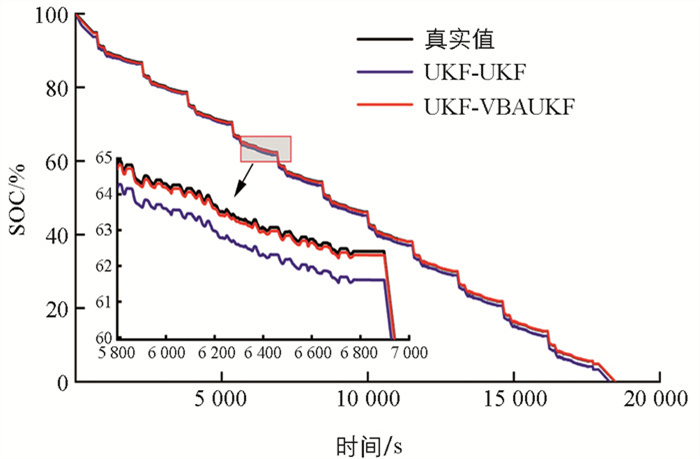
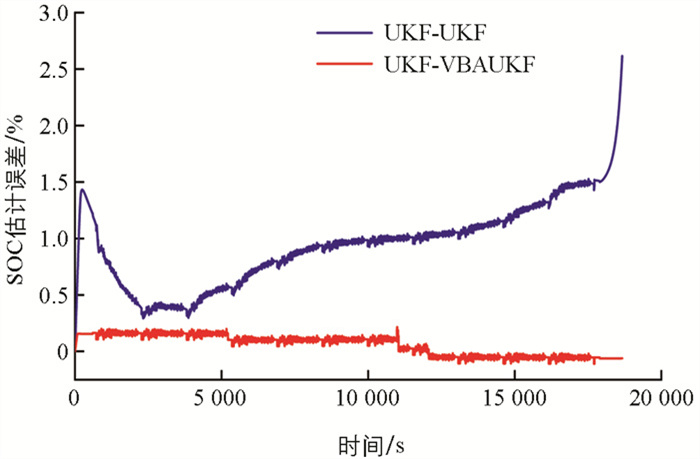
为了验证所提出的UKF-VBAUKF联合估计算法精度,对UDDS工况下参数辨识所得模型进行SOC估计,SOC的估计结果如图 7所示,2种联合估计算法对应的SOC估计误差则通过图 8进行了详细比较和呈现.
从图 7和图 8可以看出,相较于其他方法,本文提出的UKF-VBAUKF算法SOC估计结果最为接近真实值,且在整个放电过程中均能保持稳定的估计性能. 进一步分析表 1中列出的SOC误差数据,可以看出UKF-VBAUKF算法在平均绝对误差(MAE)和均方根误差(RMSE)方面的优异表现,其中MAE低至0.001 0,RMSE低至0.001 1. 这一结果表明,本文提出的UKF-VBAUKF算法有效解决了SOC估计过程中因噪声时变性带来的挑战,使得SOC的估计误差更加平稳,显著提升了估计结果的鲁棒性和准确性.
3.1. 变分贝叶斯估计原理
3.2. 结果分析
-
本文首先建立了二阶RC等效电路模型,采用UKF算法在线辨识模型参数,并且在UDDS工况下与离线辨识的端电压误差结果进行比较,验证了UKF在线辨识的模型精度. 然后引入变分贝叶斯滤波对协方差Pk和Rk进行建模并迭代预测,采用UKF-VBAUKF联合估计算法估计锂离子动力电池SOC,将SOC的MAE降低至0.001 0,RMSE降低至0.001 1,解决了复杂工况下锂离子动力电池SOC估计过程中受噪声协方差时变影响的问题. 最后在UDDS工况下与其他SOC估计算法进行对比分析,验证了本文所提算法的精确性和鲁棒性.



 下载:
下载: