-
布鲁氏菌病简称布病,是由各种布鲁氏菌所引起的,能感染家畜、野生动物和人类的世界上主要的人畜共患病之一[1-2].
最近几年,关于布病传播动力学的理论研究已经有很多[3-6].基于传播动力学的应用性研究主要集中在蒙古国和中国部分地区,这些研究主要定量评估免疫措施对布病传播的影响[7-9].文献[10]基于已检测信息建立布病传播动力学模型,研究了模型的全局动力学和周期震荡行为,给出这些动力学性态背后的生物学意义.本文以染病人数作为检测信息建立人畜耦合的布病传播动力学模型,分析平衡点的存在性,证明无病平衡点的全局稳定性和系统的持续性,研究系统的周期行为,阐述这些现象背后的流行病学意义.
全文HTML
-
人类主要是通过接触动物或者环境中的布鲁氏菌而被感染,而且恢复之后不产生持久免疫,因此,本文将人群分为两类:易感者Sh(t)与可传染者Ih(t).动物种群一般分为3类:易感者S(t)、潜伏者E(t)、可传染者I(t).总种群用N(t)表示,则有N(t)=S(t)+E(t)+I(t). M表示通过疾病流行和媒体报道而产生的有效信息的数量.易感的人和动物虽然也可通过摄取环境中的布鲁氏菌而被传染,但本文重点研究检测行为对布病传播的影响,所以本文忽略环境感染.虽然血清学检测会出现假阳性(易感动物检测呈阳性),但动物检测呈阳性还要再进行确认检测,假阳性率是比较低的,这里不考虑假阳性的情形. ϕ表示疾病意识引起的检测比率.本文以染病人数作为检测信息,并假定单位信息引起对动物种群检测的数量是
$ \phi N$ ,所以检测到有效的染病动物为$ \phi N\frac{I}{N}M = \phi IM$ .由于布病在中国是自然疫源疾病,而且国家有固定的监测点,因此,假定信息量有一个固定的输入Λ.模型建立如下:其中:A1表示人的补充率;β1表示动物对人的传染率;μ1表示人的自然死亡率;γ表示人的恢复率;A2表示动物的补充率;β2表示动物之间的传染率;μ2表示动物的淘汰率;σ表示潜伏期动物的转移率;m表示染病动物的真阳性率;对国家的固定检测点,信息量以Λ速率增加,η是染病人数转移成有效信息的转移率;d表示信息量的衰减率.
-
模型(1)的可行域为
$ \mathit{\Omega}=\left\{\left(S_{h}, I_{h}, S, E, I, M\right) | S_{h} \geqslant 0, I_{h} \geqslant 0, S \geqslant 0, E \geqslant 0, I \geqslant 0, S_{h}+I_{h} \leqslant \frac{A_{1}}{\mu_{1}}\right.$ ,$ \left.S+E+I \leqslant \frac{A_{2}}{\mu_{2}}, \frac{\mathit{\Lambda}}{d} \leqslant M \leqslant \frac{1}{d}\left(\mathit{\Lambda}+\eta \frac{A_{1}}{\mu_{1}}\right)\right\}$ .模型(1)有唯一的无病平衡点
$ \boldsymbol{E}_{0}=\left(S_{h}^{0}, I_{h}^{0}, S^{0}, E^{0}, I^{0}, M^{0}\right)=\left(\frac{A_{1}}{\mu_{1}}, 0, \frac{A_{2}}{\mu_{2}}, 0, 0, \frac{\mathit{\Lambda}}{d}\right)$ .根据下一代矩阵法[11],模型的基本再生数为为求模型(1)的地方病平衡点的存在性,令模型(1)的右端为0,则有
且I*是如下二次方程的正根
其中
则有:当R0≤1时,方程(3)没有正根,即模型(1)不存在正平衡点;当R0>1时,方程(3)仅有一个正根I*,即模型(1)存在唯一正平衡点
$\boldsymbol{E}_{*}=\left(S_{h}^{*}, I_{h}^{*}, S^{*}, E^{*}, I^{*}, M^{*}\right) $ ,其中基于以上讨论,可得以下结论:
定理1 当R0≤1时,模型(1)有一个无病平衡点E0;当R0>1时,模型(1)存在唯一正平衡点E*.
-
定理2 如果R0≤1时,模型(1)的无病平衡点E0在Ω内是全局渐近稳定的;如果R0>1时,无病平衡点是不稳定的.
证 模型(1)在无病平衡点E0处的Jacobian矩阵为:
矩阵J (E0)的特征方程为:
其中
由此可知λ1=-μ1 < 0,λ2=-μ1-γ < 0,λ3=-μ2 < 0,λ4=-d < 0,由韦达定理可知:当R0≤1时,λ5λ6>0,λ5+λ6 < 0,所以λ5 < 0,λ6 < 0,模型(1)的无病平衡点是局部渐近稳定的;当R0>1时,这里存在正根,即无病平衡点不稳定.
构造Lyapunov函数:
L沿着模型(1)的解的轨线方程求导:
1) 当R0 < 1时,L′ < 0.
2) 当R0≥1时,有S=S0,I=I0或S=S0,M=M0.
对于情况1):I′=σE≡0,意味着E=0;
$ I_{h}^{\prime}=-\mu_{1} I_{h}-\gamma I_{h}$ ,意味着$ \lim \limits_{t \rightarrow \infty} I_{h}=0$ ,从而有Sh=Sh0;M′=Λ-dM,意味着$ \lim \limits_{t \rightarrow \infty} M=M^{0}$ ,因此让L′=0的集合只包含无病平衡点.对于情况2),由M=M0得出$ I_{h}=0 . \quad I_{h}^{\prime}=\beta_{1} S_{h} I \equiv 0$ ,得出I=0,同前一种情况.因此,在这两种情况下,L′=0的最大不变集包含唯一的点E0,由LaSalle不变集原理[12]可知,当R0 < 1时,无病平衡点在Ω内是全局渐近稳定的.
定理3 对于模型(1),R0>1,疾病是一致持续的,即在Ω内,存在一个正数ε,
$\mathop {\lim \inf }\limits_{t \to \infty } (E(t), I(t)) \ge \left( {\varepsilon , \varepsilon } \right) $ .证 定义
为了证明疾病的一致持续性,在
$ \mathop {\Omega} \limits^ {\circ} $ 中,说明模型(1)的解与$ \partial \mathit{\Omega} $ 的交集是空集.首先,容易看出Ω是正不变集,
$ \partial \mathit{\Omega} $ 是闭集.根据第1个方程有这意味着
于是得出结论
根据模型(1)的第3个方程有
意味着
于是得出结论
同理根据模型(1)的第6个方程有
因此,模型(1)是点耗散.
设
满足模型(1)且
我们现在证明
$ {M_\partial } = \left\{ {\left( {{S_h}(t), 0, S(t), 0, 0, M(t)} \right):{S_h} \le \frac{{{A_1}}}{{{\mu _1}}}, S \le \frac{{{A_2}}}{{{\mu _2}}}, M \le \frac{1}{d}\left( {\mathit{\Lambda} + \eta \frac{{{A_1}}}{{{\mu _1}}}} \right)} \right\}$ .假设对所有t≥0,恒有$ \left(S_{h}(t), I_{h}(t), S(t), E(t), I(t), M(t)\right) \in M_{\partial}$ .这就证明对所有t≥0,有E(t)=0和I(t)=0.假设不成立,即存在t0≥0,可分以下2种情况讨论.1) E(t0)=0,I(t0)>0,有
由此可见,存在δ>0,当t0≤t≤t0+δ时,有E′(t)>0.这说明t0≤t≤t0+δ时,
$ \left( {{S_h}(t), {I_h}(t), S(t)} \right., E(t), I(t), M(t)) \notin {M_\partial }$ ,出现了矛盾.2) E(t)>0,I(t0)=0,有
由此可见,存在δ>0,当t0≤t≤t0+δ时,有I′(t0)>0.这说明t0≤t≤t0+δ时,
$\left( {{S_h}(t), {I_h}(t), S(t)} \right., E(t), I(t), M(t)) \notin {M_\partial } $ ,出现了矛盾.这就证明了
${M_\partial } = \left\{ {\left( {{S_h}(t), 0, S(t), 0, 0, M(t)} \right):{S_h}(t) \le \frac{{{A_1}}}{{{\mu _1}}}, S \le \frac{{{A_2}}}{{{\mu _2}}}, M \le \frac{1}{d}\left( {\mathit{\Lambda} + \eta \frac{{{A_1}}}{{{\mu _1}}}} \right)} \right\} $ .无病平衡点E0在
${M_\partial } $ 中是唯一的平衡点,下面证明当R0>1时,${W^s}\left( {{\mathit{\boldsymbol{E}}_0}} \right) \cap \mathop {\Omega} \limits^ {\circ} = \mathit{\emptyset} $ 成立.现在考虑模型(1)的几个方程由R0>1,容易得出
$\beta_{2} S^{0} \sigma>\left(\mu_{2}+m \phi M^{0}\right)\left(\mu_{2}+\sigma\right) $ .选足够小的ε>0,得到
通过直接计算,对于足够小的ε1>0,E < ε1和I < ε1,有
考虑模型(1)的任意正解
$ \left(S_{h}(t), I_{h}(t), S(t), E(t), I(t), M(t)\right)$ .假定存在T>0,对所有的t≥T,有E(t)≤ε1,I(t)≤ε1.从模型(1)的第3个方程得到,对t≥T,有
对充分小的ε1>0,存在T1>0,对所有的t≥T+T1,有
考虑一个辅助系统
注意到辅助方程关于E和I的系数矩阵有正的非对角元素.由式(6)意味着矩阵有一个正的特征值和正的特征向量ν,很容易看到当t→∞时模型(8)的任意正解趋于无穷.通过比较原则,当t→∞时,(E(t),I(t))→(0,∞).这意味着对所有的t≥T+T1,有E′(t)=β2S(t)I(t)>0.这与对所有的t≥T有E(t)≤ε1,I(t)≤ε1矛盾.所以有E0在
${M_\partial } $ 是全局稳定的,而且E0是孤立不变集和非周期的.根据文献[13]可以得到在$\mathop {\Omega} \limits^ {\circ} $ 中,模型(1)的解是一致持续的.说明当R0>1时,疾病是一致持续的.
-
对动物布病的检测可以有效控制其流行,但一般需要很大的控制力度,这关系到检测扑杀处理的费用,包括检测试剂、检测过程、扑杀带来的损失等.为了在达到控制目的的同时降低控制成本,利用最优控制理论对疫情进行时变控制.
在模型(1)中,为了分析动物布鲁氏菌病检测扑杀所需的最佳策略,修改(1)式引入依赖时间的控制量μ1(t)和μ2(t)[14],如下式所示:
控制量μ1(t)(0≤μ1(t)≤1)通过提高有效信息的数量来提高兽群中布病检测扑杀效率.控制量μ2(t)(0≤μ2(t)≤1,0表示无控制作用,1表示100%的控制作用,即所有受感染动物将通过检测从兽群中清除)模拟了检测并清除种群中受感染动物所需的努力.通过扑杀受感染的动物来控制布鲁氏菌病,需要检测动物是否受感染,这就需要业主的合作和政府适当的补偿.为了成功控制布鲁氏菌病,政府部门必须适当规划、协调和提供资源.
目标函数是将一个兽群中受感染动物(I)的数量降到最低,同时将与控制量μ1(t)和μ2(t)相关的成本尽可能降到最低. U={(μ1,μ2)|μ1,μ2在[0,T]上是勒贝格可测的}.因此,目标函数J包含一组可行的控制量μ1(t)和μ2(t)且满足有限的时间区间[0,T](T>0),即
其中B1和B2是对应的控制措施成本(权重因子).
因此,最优控制问题可以描述为
为了确定模型(9)的最优控制解,首先保证其存在最优控制解.通过以下定理给出:
定理4 考虑模型(9)的控制问题,存在一个最优控制
$ \overrightarrow{\boldsymbol{\mu}}^{*}=\left(\mu_{1}^{*}, \mu_{2}^{*}\right)$ ,其中$\mu_{1}^{*}, \mu_{2}^{*} \in U $ ,使得证 这里应用最优存在理论[15]来证明这个定理.
(ⅰ)对任何控制变量μ1,μ2∈U和模型(9)的初始状态变量都是非空的;
(ⅱ)控制集U是闭集且是凸集;
(ⅲ)模型(9)的右边的线性函数满足初始条件,所以在控制集U上是有界的;
(ⅳ)目标函数(10)中的被积函数在控制集U上是凸集,且存在常数c1,c2>0使得
因为
$I \geqslant 0, \frac{1}{2} B_{1} \mu_{1}^{2}+\frac{1}{2} B_{2} \mu_{2}^{2} \geqslant \frac{1}{2} \min \left\{B_{i}\right\}\|\mu\|^{2} $ ,所以取$ c_{1}=\frac{1}{2} \min \left\{B_{i}\right\}, c_{2}=2$ 可以满足(12)式.综上所述,模型(9)存在最优控制解.由文献[16]导出了最优控制必须满足的必要条件.定义(11)式的哈密顿量H为
其中
$ \lambda s_{h}, \lambda_{I_{h}}, \lambda_{S}, \lambda_{E}, \lambda_{I}$ 和λM是各状态的伴随变量.通过对H各状态变量微分,可以得到各伴随变量的微分方程,即
从而得出
而且满足横截条件
通过求哈密顿方程(13)对各控制变量的偏导数可以得到导数等于零的控制点,从而有最优控制解,即
结合各控制量的边界条件,通过求解方程(16)得到
其中λI,λM可以通过解方程组(14)得到.
权重的真实值需要通过大量的实地调查和数据挖掘获得.在已知真实权重值的情况下,在目标函数中加入补助项可以改善计算结果.在研究中J中包含I(t)项不会对这个最优控制问题的总体结论产生重大影响,但对我们未来的控制问题很有帮助.
-
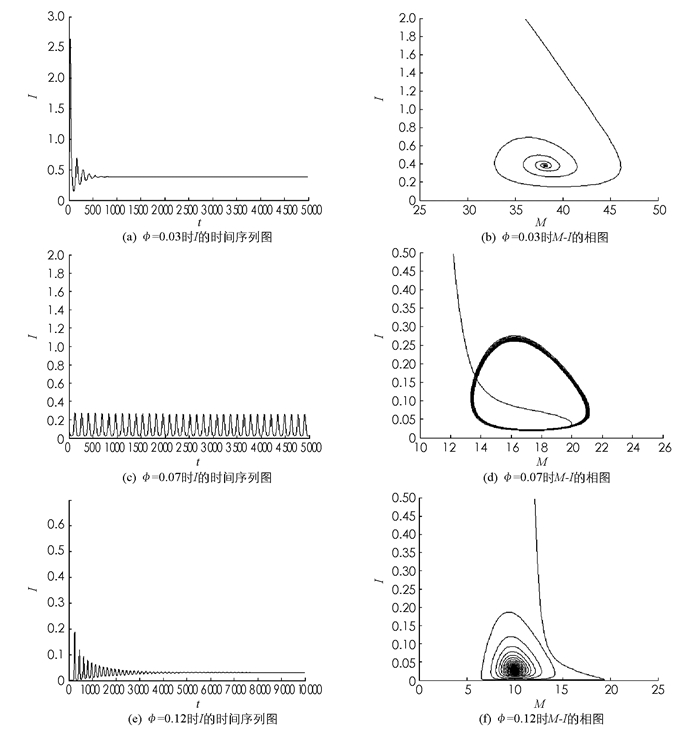
利用数值模拟的方法分析模型(1)在地方病平衡点E*处的动力学性质.所取参数A1=1,β1=0.1,μ1=0.06,γ=0.001,A2=60,β2=0.03,μ2=0.3,σ=0.1,m=1,Λ=0.12,η=0.1,d=0.02.图 1是数值模拟图,其中:(a),(c),(e)分别表示ϕ值不同时关于I的时间序列图;(b),(d),(f)表示ϕ值不同时M和I的相图.图 1(a)是ϕ=0.03时关于I的时间序列图,曲线最后趋于一条直线,平衡点是全局稳定的;图 1(c)是ϕ=0.07时关于I的时间序列图,曲线产生周期性的震荡;图 1(d)中曲线最后趋于一个环,由此可知在这种情况下模型(1)在地方病平衡点E*处会出现分支;图 1(e)是ϕ=0.12时关于I的时间序列图,周期解消失,曲线再次趋于一条直线.ϕ的值从小到大,周期解从无到有,然后再消失,说明检测比率的变化对模型的动力学有很大的影响,从而对疾病的控制起到极其重要的影响.对于模型(9),由于没有进行实地的考察和调研,对权重因子没有一个有价值的估计,所以模拟的结果没有大的实用价值.
本文基于布病传播的具体特点,建立反映检测行为的动力学模型,通过分析这个模型,发现检测对模型的动力学性质有显著的影响.周期震荡行为的出现会严重影响防控措施的有效执行(例如疫病在周期运行的最低点,人们可能误认为疫病开始消失).因此,在对动物进行检测时,结合最优控制解,适当提高动物的检测比率,可使布病得到较好控制.



 下载:
下载: