-
关于HIV病毒感染问题已有大量研究[1-10].本文在HIV病毒基本动力学模型的基础上考虑分阶段细胞免疫生成机制,得到如下动力学模型:
其中:X(t),Y(t),V(t),W(t),Z(t)分别表示t时刻健康细胞、感染细胞、游离病毒、免疫初期细胞、成熟免疫细胞的数量;s为健康细胞的出生率,α为感染率,k为病毒的产生率,η为免疫细胞激发率,p为免疫率;d表示病毒死亡率,di(i=1,2,3,4)分别表示健康细胞、感染细胞、免疫初期细胞、成熟免疫细胞的死亡率,δ=μ d3为免疫初期到成熟免疫细胞的转化率,μ是由免疫初期细胞转化为成熟免疫细胞的存活率.借助拟平衡态的方法[10],假设病毒已经处于平衡态,将系统(1)转化成下面的系统:
其中
$ \beta = \frac{{\alpha k}}{\rm{d}}$ .假设非负初始条件:X(0)≥0,Y(0)≥0,W(0)≥0,Z(0)≥0.
全文HTML
-
定理1 存在正常数
$ M = \frac{s}{{{\rm{min}}\{ {d_1}, {d_2}, {\rm{ }}{d_3}\} }}$ ,系统(2)的正不变集为:证 对任意(X,Y, W,Z)∈Γ,有
故对于给定的非负初始条件,X(t)和Y(t)均是非负的.
下面证明W和Z的非负性.假设存在最小的tw使得W(tw)=0,Z(tw)>0.此时有
$ \frac{{{\rm{d}}W}}{{{\rm{d}}t}}\left| {_{{t_w}}} \right. = \eta YZ \ge 0$ ,即当W到达0,导数会大于等于零,也即非负;假设当t=tz>tw时,Z=0,此时注意到$ \frac{{{\rm{d}}Z}}{{{\rm{d}}t}}\left| {_{{t_z}}} \right. = \delta W \ge 0$ ,故Z非负;假设W与Z同时到达0,此时有$\frac{{{\rm{d}}W}}{{{\rm{d}}t}} = 0 $ ,$ \frac{{{\rm{d}}Z}}{{{\rm{d}}t}} = 0$ ,故说明了W与Z的非负性,至此证明了解的非负性.为了证明系统的有界性,我们引入新的变量
$ Q = X + Y + \frac{p}{\eta }W$ ,则由解的非负性可得根据(3)式和比较原理可得
再由系统(2)的第4个方程可得:
由根据(4)式和比较原理可得
定理证毕.
-
系统(2)总是存在无感染平衡点
$ {E_0} = \left( {\frac{s}{{{d_1}}}, {\rm{ }}0, {\rm{ }}0, {\rm{ }}0} \right)$ .计算基本再生数可得定义
故
易得如下定理2.
定理2
$ \left( {\rm{i}} \right)\;$ 当R0>1时,系统(2)存在唯一的免疫未激发平衡点${\mathit{\boldsymbol{E}}_1} = \left( {\frac{{{d_2}}}{\beta },\frac{{s\beta - {d_1}{d_2}}}{{{d_2}\beta }},0,0} \right)$ ;$\left( {{\rm{ii}}} \right) $ 当R1>1时,系统(2)存在唯一的免疫激发平衡点E2=(X2,Y2,W2,Z2).下面为了研究平衡点的局部稳定性,先给出系统(2)的雅可比矩阵为:
定理3 当R0<1时,系统(2)的无感染平衡点E0是局部渐近稳定的;当R0>1时,系统(2)的无感染平衡点E0是不稳定的.
证 系统(2)在E0处的特征方程为
所以当
$ {d_2} - \frac{{\beta s}}{{{d_1}}} > 0$ ,即R0<1时,特征方程(5)的所有根均是负的,从而知E0是局部渐近稳定的;当R0>1时,系统(2)的无感染平衡点E0是不稳定的.定理4 当R0<1时,系统(2)的无感染平衡点E0是全局渐近稳定的.
证 构造如下Lyapunov函数
对函数U求导并带入系统(2)可得
当R0<1时,
$ \frac{{{\rm{d}}U}}{{{\rm{d}}t}} \le 0$ ,同时注意$\frac{{{\rm{d}}U}}{{{\rm{d}}t}} = 0 $ 仅包含系统的无感染平衡点E0,再由Lassal不变原理可知,系统(1)的无感染平衡点E0是全局渐近稳定的.定理5 假设R0>1.当R1<1时,免疫未激发平衡点E1局部渐近稳定;当R1>1时,免疫未激发平衡点E1是不稳定的.
证 系统(2)在E1处的特征方程为
所以当
$ {d_3}{d_4} - \frac{{\eta \delta {d_1}({R_0} - 1)}}{\beta } > 0$ ,即R1<1时,特征方程(6)的所有根均是负的,知免疫未激发平衡点E1是局部渐近稳定的.定理6 假设R1>1.则当
$ \frac{{\eta \delta }}{\beta } < {d_1} + \frac{{\beta {d_3}{d_4}}}{{\eta \delta }} < {d_3} + {d_4}$ 时,系统(2)的免疫激发平衡点E2=(X2,Y2,W2,Z2)是局部渐近稳定的.证 系统(2)在E2处的特征方程为
其中:
显然Ai>0,i=1,2,3,4.根据特征方程(7)和Routh-Hurwitz稳定性判据可知,E2是局部渐近稳定的当且仅当(A1A2-A3)A3-A12A4>0,即
当
$ \frac{{\eta \delta }}{\beta } < {d_1} + \beta {Y_2} < {d_3} + {d_4}$ 时,可得从而知(A1A2-A3)A3-A12A4>0,即知系统(2)的免疫激发平衡点E2=(X2,Y2,W2,Z2)是局部渐近稳定的.
-
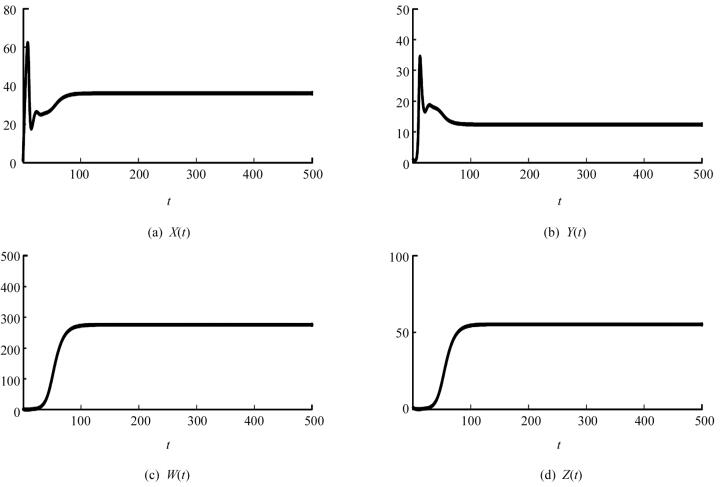
取一组参数s=10,β=0.02,d1=0.03,d2=0.5,d3=0.99,η=0.4,p=0.004,δ=0.1,d4=0.5,则可以计算出基本再生数R0=13.333 3,平衡点X2=36.036 0,Y2=12.375 0,W2=275.900 9,Z2=55.180 2.同时通过计算可知此时(A1A2-A3)A3-A12A4>0,知免疫激发平衡点E2是局部渐近稳定的(图 1).
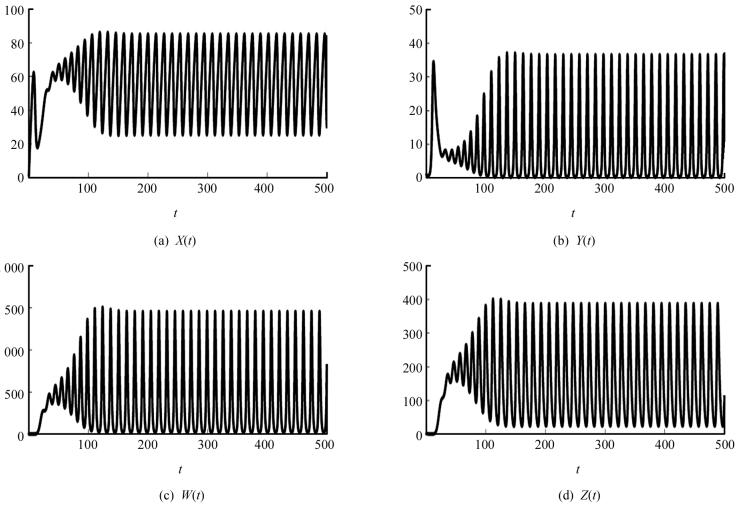
取定另一组参数s=10,β=0.02,d1=0.03,d2=0.5,d3=0.99,η=0.4,p=0.004,δ=0.2,d4=0.5,则可以计算出基本再生数R0=13.333 3,平衡点X2=65.040 7,Y2=6.187 5,W2=500.508 1,Z2=200.203 3.此时计算得出(A1A2-A3)A3-A12A4<0,所以系统(2)的免疫激发平衡点E2是不稳定的,存在周期震荡现象(图 2).
-
通过建立考虑分阶段免疫细胞生成机制的HIV病毒感染模型,研究了无感染平衡点和免疫未激发平衡点以及免疫激发平衡点的局部和全局稳定性.通过以往的相关研究,知道如果免疫细胞的生成不分阶段,免疫激发平衡点是全局稳定的.本文研究发现,如果免疫细胞分阶段生成,则免疫激发平衡点是条件局部稳定的,也就是说系统可能会通过Hopf分支而产生周期解.研究表明免疫细胞的生成机制对病毒动力学性态具有关键的影响.接下来的研究工作是希望进一步从理论上证明相关Hopf分支的方向、稳定性等问题.



 下载:
下载: