重庆市在两江、四山的天然屏障分割下，形成了“多中心组团式”的城市空间结构，被认为是典型的多中心城市，也是学者们研究的重要对象^[8].根据《重庆市城乡总体规划(2007-2020年)》，都市区空间结构为6个城市副中心和16个组团.六大城市副中心是除中央商务区外，杨家坪、沙坪坝、观音桥(至新牌坊地区)、南坪、西永、茶园等地.其中，西永和茶园是新增的城市副中心. 16个组团是“多中心组团式”空间结构的基本组成单位，是片区内相对独立的城市建设区域.因此，本文将组团作为研究的基本单元(图 1). 2012年，重庆市房地产开发增长较快，主城区房价的空间差异十分明显.其中，位于主城中心的渝中组团价格最高，为8 365元/m²；向北向南向西有3个高价中心，向北的高价区域为观音桥组团，向南为南坪组团，价格都在6 200~6 600元/m²之间；向西的高价区域为大杨石组团，价格在5 200~5 900元/m²之间.可见，高价区域与城市规划相吻合，具有多中心的特征.

引力模型是地理学中定量揭示城市空间相互作用的重要模型，是在万有引力定律的基础上逐渐发展而来，它主要是为了反映地区间各要素的相互联系性，并在一定地域范围内精确地进行空间结构分析^[7].因此本文使用该模型进行地价空间结构的研究，并将多中心城市的引力模型定义为：在多中心城市系统中，2个组团间的引力与组团质量、区域调节系数成正比，与距离的平方成反比.公式为：

式中：F_ij为城市i，j组团之间的引力；r_i为区域调节系数；M_i，M_j分别为i，j组团的质量值； D_ij为i，j组团之间距离.

城市地价是多种地理要素作用在不同地区的结果，而不同的组合形式表征出了地价的空间分异.在多中心城市引力模型中，将可能影响地价的各要素对地价作用的综合效应值定义为相应的城市组团质量^[7].它主要包括2个层次：一个是组团质量的核心层次，即组团本身的发展程度；另一个是组团质量的区域层次，即组团的经济集聚扩散能力以及其所在区域的协调发展程度.因此本文试图从这2个层次出发来体现城市组团质量.

首先，设计指标体系.在参考已有学者研究成果的基础上，根据区域差异性、客观性、针对性和数据可获取性等原则来确定评价指标体系，主要包括3个层次：集聚度、开发规模和设施完善度(表 1).

然后使用极值标准化法对各指标数据进行无量纲处理，再用变异系数法来确定各指标权重，最后测算城市组团质量时，采用综合指数法对各项指标加权求和后得到各组团的质量值.

本文以2012年重庆主城区道路与轨道交通相结合的矢量数据为基础，借助GIS技术平台的空间分析功能，对重庆组团之间的空间距离进行测算.具体做法：首先，根据重庆各组团的分布状况提取出各组团的几何中心，并在重庆市道路网络的矢量数据基础上生成一个新的网络数据集；然后通过ArcGIS 10.2中的Network Analyst构建OD成本矩阵，分别导入各组团的几何中心，再应用OD成本矩阵工具测算出各组团之间的距离.

在参考以往学者对引力模型中区域调节系数解释和修正的基础上，将可达性作为区域调节系数^{[7, 9-10]}.因为对于城市这样具体的经济主体，除空间距离外，还应包含一定的非空间要素.可达性作为衡量两地联系密切程度的重要指标，可反映空间实体之间克服距离障碍的难易程度，所以被用来修正引力模型.根据《重庆市城市道路交通规划及路线设计规范》，将重庆的城市道路体系划分为快速路、主干道、次干道、隧道、桥梁、轻轨等，在重庆道路网络矢量数据中根据道路级别分别附上其计算行车速度，然后通过Network Analyst，计算出每个组团到其他组团的最短时间求和，作为这2个组团间的可达性系数.

本文数据的来源：1) 2012年各组团地价水平值来源于城市地价动态监测年度成果；2) 各组团质量指标数据主要来源于《重庆市城乡总体规划(2007-2020)》和《国民经济和社会发展统计公报》(2012年)等；3) 城市道路矢量数据等来源于重庆市地理信息公共服务平台.

根据多中心城市引力模型的公式，分别测算出各组团之间发生相互作用所产生的引力，引力的大小定量地反映了各组团之间相互作用和联系的强弱.综合影响力指数是某组团与区域内所有组团之间发生相互作用所产生引力的总和，反映了区域因素对某组团的影响力和该组团对外联系总量的强弱^[7](表 2).

从表 2可以看出，区域因素对大杨石组团的综合影响力最大，观音桥—人和、渝中、南坪、沙坪坝和大渡口组团次之，其余组团受到区域的影响力均很小.这是由于大杨石、观音桥—人和与渝中组团都是城市中心的重要组成部分，处于交通枢纽位置，通达性系数都比较高，所以与其他组团都建立了紧密的空间联系，受到区域的综合影响力都很大.但作为中央商务区的渝中组团由于建设密度过高，用地开发趋于饱和，组团质量受到可开发规模的限制，所以综合影响力相对减弱.其他3个次中心组团(南坪组团、沙坪坝组团和大渡口组团)则发展较为均衡，公共服务面向周围的区域范围，综合影响力指数较高且相差不大.而其他外围组团与相邻的次中心组团由于被山体和江河阻隔，独立地发展本地的生产生活体系，所以与其他组团之间的联系不紧密，综合影响力指数很小.

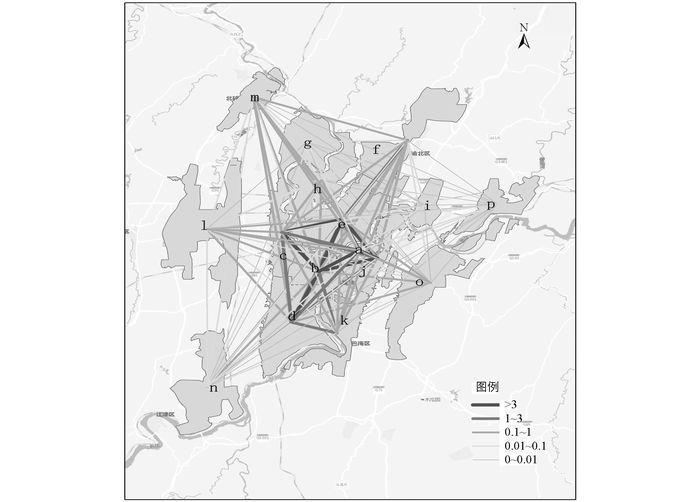
在多中心城市的区域系统中，组团间相互作用的强弱反映了彼此之间联系的密切程度，组团间相互作用强度如图 1所示.从组团之间的相互作用强度来看，观音桥—人和、南坪、大杨石、沙坪坝组团与渝中组团之间的相互作用远大于其他组团.其中，观音桥—人和组团最高，联系强度最大.说明主中心与次中心的联系十分紧密，次中心发展很迅速，并有效地协调了主中心与外围组团的极化效果，增强中心组团与外围组团的再生产联系，使中心组团的作用力辐射范围更广、扩散更快.相对于中心组团的密切联系性，位于边缘的鱼嘴、西彭、西永、北碚和唐家沱组团与区域内其他组团两两相互作用强度均小于1，组团间联系受限，说明外围组团表现出了一定的离心性.所以对外围组团应加大次中心组团的辐射强度，提供就近的商贸服务，均衡布局公共服务设施.虽然外围组团在地理位置上相互分隔，但可通过功能上的互补性来增强彼此间的空间联系，使其尽快融入到重庆主城体系中来.

同时，从图 1可以看出，位于南北片区的两路组团和大渡口组团与中心组团的相互作用比位于东西片区的茶园-鹿角组团和西永组团的相互作用强度更大一些，说明中心组团有向南北方向扩散的趋势.可能由于西永和茶园作为新增的城市副中心，还有待发展，所以组团间影响还没有充分发挥作用，所以应尽早完善西永组团和茶园组团内部的功能区建设，推动其快速成为新的次中心组团，并使之迅速崛起以带动主城向东西南北4个方向挺进，逐渐形成“一主中心—六次中心—外围组团”的空间格局.

1992年重庆完成了城镇土地定级和基准地价评估，2000年对城镇土地级别进行了调整和基准地价及其修正体系的更新，为科学有效地管理土地资源提供了参考依据^{[11, 12]}.根据当前重庆市基准地价更新成果，以2012年7月3日为地价基准日，统计出各组团商服用途、住宅用途和工业用途的最高级别基准地价.统计表明，在商服用途中，渝中组团、观音桥—人和组团和南坪组团最高，西彭组团和鱼嘴组团最低；住宅用途中，渝中组团、观音桥—人和组团、大杨石组团、沙坪坝组团和南坪组团的地价水平最高，鱼嘴最低；工业用途中，大杨石组团和南坪组团最高，西彭组团、北碚组团和鱼嘴组团最低.

1) 商服用地

以各组团综合影响力指数为自变量，商服用地最高基准地价为因变量，运行结果计算出相关系数R=0.850，拟合优度R²=0.722，说明商服用地最高基准地价和综合影响力指数的相关性分析具有统计学意义，模型拟和效果较好，线性回归方程为：

2) 住宅用地

同上，R=0.846，拟合优度R²=0.716，说明商服用地最高基准地价和综合影响力指数的相关性分析具有统计学意义，模型拟和效果较好，线性回归方程为：

3) 工业用地

同上，R=0.784，拟合优度R²=0.615，说明商服用地最高基准地价和综合影响力指数的相关性分析具有统计学意义，模型拟和效果较好，线性回归方程为：

综合影响力指数与各用途最高基准地价的相关性分析具有统计学意义(p＜0.05)，在空间分布上基本一致，这表明了各组团之间的相互作用与城市地价分布呈现正相关关系，空间相互作用是影响城市地价水平的因素之一，并且商服用地和住宅用地的相关性较强.

由于城市基准地价和综合影响力指数呈正相关关系，所以按照综合影响力指数划分的等级可以代表各组团地价等级.结合商服、住宅及工业预测值和级别划分结果，可将重庆16个组团的地价划分为3个等级(表 3).由表 3可以看出，重庆组团的地价分布具有明显的空间差异性，各组团地价呈多中心、镶嵌式分布特征，并沿圈层逐步递减.其中，第一圈层仍具有较大的吸引力，观音桥—人和、杨家坪和渝中组团之间的相互作用最强，使得主次中心之间联系紧密，集聚能力不断增强，所以地价最高.第二圈层集聚能力减弱，但各次中心组团与中心组团和外围组团之间的联系都比较密切，且各自相对独立发展均衡，使其地价与中心组团之间差距不大.而第三圈层呈下降趋势且外围组团发展速度缓慢，西永和茶园副中心的城市功能配置和产业园区还有待完善，外围组团与次中心组团间的联系仍需进一步推动，所以地价水平较低.由此可以看出，对多中心组团城市进行有效的空间引导和规制，加快其有序发展进程，可以促进地价的空间协调管理.

本文从多中心城市空间相互作用的角度出发，借助引力模型，探讨组团间相互作用对多中心城市地价的影响，并以典型的多中心城市重庆为例，进行实证检验，主要得出以下结论：

1) 在测算多中心城市地价时，空间相互作用因素的影响不容忽视.组团地价的确定，既取决于其自身的内部要素，又与区域内其他组团的相互作用有关，空间相互作用因素应作为地价的一个重要影响因子加以考虑.

2) 引力模型能够较好地分析组团间相互作用对地价的影响，其测算结果与基准地价分布基本上吻合.在引力模型中，考虑了城市组团质量、交通距离和区域调节系数等重要因素.组团质量水平越高，距离越近，可达性越好，组团间相互作用越强烈，对组团地价的综合影响程度就越大.

随着城市空间结构的不断优化，重庆组团间的联系将更为密切，研究出如何更好地发挥组团的“外部效益”和“协同作用”，强化核心组团的集聚功能，培养区域内各组团中心功能的互补性，构建区域内的联系通道，加强重庆主、次中心组团与外围组团之间的跨界治理和合作，将有助于更好地进行地价管理，促进组团间地价的协调发展.