本文考虑欧式多因子期权的定价问题.在风险中性世界中，这等价于求一个如下高维积分问题：

其中：$\boldsymbol{X}$是$n$维标的资产的状态变量，其概率密度函数为$f(x)$，$F(\boldsymbol{X})$是贴现收益函数.多因子指的是标的资产状态变量$\boldsymbol{X}$，它的“多”可能来源于标的资产的高维性，如多资产期权，或者标的资产的路径依赖性，如亚式期权的收益函数典型地依赖于多个时间状态的值.

经典的蒙特卡罗(classical Monte Carlo, CMC)方法可以用来解决这一类期望问题.首先根据密度函数$f(x)$生成容量为$N$的随机样本$X^{(i)}(i=1，2，…，N)$，然后计算每一个样本函数的值$V^{(i)}=f(\boldsymbol{X}^{(i)})$，最后计算样本均值

则样本均值$\bar{V}_{N}$就是期权价格$E[V]$的一个无偏估计.如果随机样本$V^{(i)}$具有有限方差$σ^{2}$，中心极限定理说明样本的误差满足

其成立的概率为1-α，其中$z_{1-\frac{α}{2}}$是标准正态分布的$1 - \frac{\alpha }{2}$分位数.于是蒙特卡罗方法的有效性可以用样本的标准误差$std(\bar{V}_{N})=\frac{σ}{\sqrt{N}}$来度量.可以看出，蒙特卡罗方法的收敛性速度非常慢，仅为$O(N^{-1/2})$.对多因子期权定价问题，考虑到标的状态变量的高维性，即使生成一个简单随机样本也需要大量的时间.

控制变量(control variate)技巧是一种常用的方差减小技术，它利用一个已知量的估计误差来降低未知量的估计误差^[2].使用控制变量技巧可以大大提高蒙特卡罗模拟的效率.为了说明其思想，考虑问题(1)，即计算随机变量V的期望$E[V]$.在得到$V^{(i)}$的同时能得到另一个随机向量$\boldsymbol{C}=(C_{1}，C_{2}，…，C_{d})^{\text{T}}$的样本$\boldsymbol{C}^{(i)}$，且其期望$E[\boldsymbol{C}]$已知.假设随机样本$(\boldsymbol{C}^{(i)}，V^{(i)})$具有如下的协方差矩阵

其中$\text{Σ}_{C}$是非奇异的$d×d$方阵，$\text{Σ}_{CV}$是$d×1$向量，常数$σ^{2}_{V}$是变量$V$的方差.对任意固定的向量$\boldsymbol{b}∈\mathbb{R}^{d}$，可以构造$E[V]$的一个估计值

其中误差$\bar{\boldsymbol{C}}_{N}-E[\boldsymbol{C}]$是可以观察的，这就成为未知误差$\bar{V}_{N}-E[V]$的一个控制，把$\boldsymbol{C}$称为$V$的一个控制向量或者多元控制变量.显然控制变量估计值$\bar{V}_{N}(\boldsymbol{b})$是一个无偏估计，并且可以选择如下的最优系数

使得估计值方差最小为

其中$R^{2}_{CV}$是平方复相关系数，它度量了使用控制变量$\boldsymbol{C}$后$V$的方差减小比例.于是，控制变量方法的效率可以用方差减小指数

来度量.方差减小指数对控制向量$\boldsymbol{C}$和原始变量$V$之间的相关系数$R_{CV}$高度敏感，如果$\left|R_{CV}\right|$趋向于1，则方差减小指数可以大幅度提高.这说明，为了有效地减小方差，必须要选择一个与原始变量高度相关的控制向量.当然，控制向量的选择取决于具体的问题，对于期权定价问题，标的资产、债券价格、对冲等都可以作为控制变量.

特别地，当多元控制变量$\boldsymbol{C}$的各个分量独立时，此时协方差矩阵$\text{Σ}_{C}$是对角矩阵.于是，平方复相关系数

其中$ρ_{C_{i}V}$是控制变量$C_{i}$与$V$的相关系数.这也说明，如果控制变量之间相互独立，使用的控制变量个数越多，那么其方差减小效果越好.

主成分分析((principle component analysis, PCA))是一种对多维随机变量的统计降维方法.更准确地说，它是将研究对象的多个相关变量近似地转化为少数几个独立变量的一种多元统计方法^[9].在多变量统计分析中，为了尽可能完整地搜集信息，对每个样品往往测量许多指标，这虽然可以避免重要信息的遗漏，然而从统计的角度来看，这些变量可能高度相关，反而增加了问题的复杂性.因此，自然想到用少数几个不相关的综合变量来代替原来较多的相关变量，而不损失原始变量的大部分信息.

对标的资产的状态变量$\boldsymbol{X}=(X_{1}，X_{2}，…，X_{n})^{\text{T}}$，假设其均值向量和协方差矩阵分别为$\boldsymbol{\mu}_{X}，\text{Σ}_{X}$.显然$\text{Σ}_{X}$是一个半正定对称矩阵，于是有谱分解

其中

是特征值组成的对角矩阵，且$λ_{1}≥λ_{2}≥…≥λ_{n}≥0$.而$\boldsymbol{U}=(\boldsymbol{u}_{1}，\boldsymbol{u}_{2}，…，\boldsymbol{u}_{n})$是一个正交矩阵，$\boldsymbol{u}_{i}$是特征值$λ_{i}$对应的特征向量.于是，$\boldsymbol{X}$的主成分变换为

此时，贴现收益函数$F(\boldsymbol{X})$变为$g(\boldsymbol{Y})$，期权定价问题(1)等价于

显然(5)式定义的主成分$\boldsymbol{Y}$具有零均值. $\boldsymbol{Y}$的第$i$个分量$Y_{i}=\boldsymbol{u}^{\text{T}}_{i}(\boldsymbol{X}-\boldsymbol{\mu}_{X})$称为第$i$个主成分(principle component, PC).显然，$\boldsymbol{Y}$的协方差矩阵就是Λ，也就是说$\text{var}(Y_{i})=λ_{i}$，并且$\text{cov}(Y_{i}，Y_{j})=0，i≠j$.第$i$个主成分$Y_{i}$的贡献率定义为

这说明了$Y_{i}$对原变量的信息解释能力.前$q$个主成分的解释能力可以用累计贡献率$ψ_{q}$来度量，

$ψ_{q}$越大，说明前$q$个主成分的解释能力越强.

现在，对多因子期权定价问题(6)，利用主成分可以构造多元控制变量，我们称这种模拟方法为主成分蒙特卡罗(principle component Monte Carlo, PCMC)方法.

采用式(7)中定义的累计贡献率$ψ_{q}$作为标准，如果特征值$λ_{1}$相对于$λ_{2}$很大，则第一个主成分$Y_{1}$可以解释原始变量$\boldsymbol{X}$的绝大部分信息.自然，$Y_{1}$可以用来构造一个控制变量

如果$λ_{1}$相对于$λ_{2}$不是很大，那么在使用$Y_{1}$的同时，可以使用第二个主成分$Y_{2}$一起来解释$\boldsymbol{X}$的信息.同时使用$Y_{1}$，$Y_{2}$构造的一个控制变量是

理论上，可以用前$k$个主成分$Y_{1}，Y_{2}，…，Y_{k}$构造如下的控制变量

实际上，上面构造的控制变量可以从另一个角度来理解.在$n$维积分问题(6)中，如果特征值$λ_{2}，…，λ_{n}$相对于$λ_{1}$很小，这说明主成分$Y_{2}，…，Y_{n}$的方差也很小，于是可以把它们近似看作是常数.也就是说，在积分(6)中，$Y_{2}，…，Y_{n}$可以用它们的期望值0代替，于是就得到了$C^{1}$.$ C^{1}$自然地可以看作是贴现收益函数的一个近似.同样地，$C^{k}$也可以看作是贴现收益函数的一个近似.它们都可以用作蒙特卡罗模拟的控制变量.

一个好的控制变量必须容易得到它的期望，并且与原始变量高度相关.在实际中，考虑到计算的复杂程度，运用最多的还是$C^{1}$，$C^{2}$，$C^{3}$.

为了避免计算形如$C^{k}$这样的高维积分，可以使用单个的主成分构造如下的控制变量：

$C_{k}$的期望$E[C_{k}]$是一个一维积分，采用一些数值方法容易得到.由于主成分$Y_{k}$是按照它们的重要程度降序排列的，可以猜测$C_{k}$与贴现收益函数$g(\boldsymbol{Y})$之间的相关性也随着$k$增大而减小.由于$Y_{1}，Y_{2}，…，Y_{k}$之间是相互独立的，所以控制变量$C_{1}，C_{2}，…，C_{k}$之间也是独立的，使用多元控制可以得到更好的方差减小效果.

如果从贴现收益函数$g(\boldsymbol{Y})$的近似表达来看，$C^{k}$显然比$C_{1}，C_{2}，…，C_{k}$的精确程度更高，当然也具有更高的相关系数.于是，可以提出一种混合的多元控制变量，即使用$C^{k}，C_{k+1}，…，C_{p}(p≤n)$.注意到$C^{1}=C_{1}$.在下文中，我们将使用形如$C^{2}，C_{3}，…，C_{k}$的控制变量.

假设欧式多资产期权的标的资产$\boldsymbol{S}=(S_{1}，S_{2}，…，S_{n})^{\text{T}}$满足如下的随机微分方程(SDEs)^[11]：

其中：$r$是市场无风险利率，$d_{i}$是股票$S_{i}(t)$的连续分红率，$σ_{i}$是$S_{i}(t)$的波动率，$W_{i}(t)(i=1，2，…，n)$是标准布朗运动，且具有如下的相关系数矩阵

对于欧式多资产期权，设其在到期日T的收益函数为$h(\boldsymbol{S}(T))$，则其在初始时刻的价值为

令

则$\boldsymbol{X}$是一个$n$维正态随机向量.并且$\boldsymbol{X}$的期望为零，协方差矩阵为

从而随机微分方程(8)的解为

于是，期权价格$V$具有显性表达式

假设$\boldsymbol{X}$的协方差矩阵有谱分解$\text{Σ}=\boldsymbol{U}$Λ$\boldsymbol{U}^{\text{T}}$，其中Λ$=\text{diag}(λ_{1}，λ_{2}，…，λ_{n})$是特征值组成的对角矩阵，$\boldsymbol{U}=(\boldsymbol{u}_{1}，\boldsymbol{u}_{2}，…，\boldsymbol{u}_{n})$是一个正交矩阵，其元素$\boldsymbol{u}_{i}$是特征值$λ_{i}$对应的特征向量.则$\boldsymbol{X}$的主成分变换为

于是收益函数$h(\boldsymbol{S}(T))$变为$g(\boldsymbol{Y})=g(Y_{1}，Y_{2}，…，Y_{n})$，再注意到$\boldsymbol{Y}$的协方差矩阵就是对角阵Λ，从而可以将式(11)改写为

一篮子期权是一种典型的多资产期权，其收益函数取决于标的资产的平均数.对算术平均一篮子期权，在到期日T的欧式看涨期权的收益函数可以记作

其中：第$i$个资产价格$S_{i}$服从(8)式定义的几何布朗运动，$ω_{i}$是对应的权重，$ω_{i}≥0，∑ω_{i}=1$，$K$是敲定价格.对算术平均一篮子期权，即使是欧式期权，我们也无法得到其封闭解.然而，我们容易得到对应的几何平均一篮子期权的价格^[11].

为了说明算法的有效性，我们不妨从一个2维的一篮子期权说起.此时，它的收益函数为

利用主成分变换(12)式，收益函数变为

此时，期权价格可以表示为

我们可以构造两个独立的控制变量

蒙特卡罗控制变量模拟算法如下：

1) 生成独立的标准正态随机变量$Z^{(i)}_{1}，Z^{(i)}_{2}(i=1，2，…，N)$，$N$是给定的模拟路径数；

2) 计算收益函数

及控制变量

3) 根据(4)式计算最优系数$b_{1}$和$\boldsymbol{b}_{2}$；

4) 得到蒙特卡罗估计值

以及主成分控制变量(PCMC)估计值：

为简单起见，令$ω_{1}=ω_{2}=\frac{1}{2}$，分红率d$_{1}=d_{2}=0$.模拟的路径数$N$=100 000.

由于波动率对期权价格具有显著影响，下面主要考虑波动率对蒙特卡罗模拟方法的影响.令

经过计算，此时对协方差矩阵谱分解后特征值之比为$\frac{λ_{1}}{λ_{2}}=3$.试验结果见表 1.

表 1展示了几种蒙特卡罗模拟的期权价格，括号里是对应的样本标准差.其中精确值是使用数值算法得到的精确解1，CMC表示普通的蒙特卡罗模拟方法，GMC是使用几何平均一篮子期权作为控制变量，PCMC-(14)表示的是使用式(14)的一元控制变量，PCMC-(15)表示的是使用式(15)的二元控制变量.明显看出，在各种波动率情形下，构造的二元控制变量PCMC-(15)具有最小的标准差，其次是一元控制变量PCMC-(14)，它们均优于使用几何平均一篮子期权作为控制变量.另外，随着波动率的增加，期权价格也在增加，模拟的标准差也在增加，但是3种控制变量方法的方差减小指数却在减小.

当$σ_{1}=σ_{2}=0.4$时，协方差矩阵的特征值为$λ_{1}=0.24，λ_{2}=0.08$.现在固定$λ_{1}$，改变特征值的比例$\frac{λ_{1}}{λ_{2}}$或者$λ_{2}$，观察试验结果，见表 2.

表 2说明3种控制变量的方差减小指数随着$\frac{λ_{1}}{λ_{2}}$的增大而增大.当$\frac{λ_{1}}{λ_{2}}$增大时，$C_{1}=g(Y_{1}，0)$对收益函数$g(Y_{1}，Y_{2})$的近似就越好，它们之间的相关系数就越高，从而方差减小指数就越大.注意到方差减小指数与$\frac{1}{1-ρ^{2}}$成比例，这说明当$|ρ|$趋近于1时，方差减小指数迅速增加.这也说明，此时对相关系数的一点点提高都会使得方差减小效果大幅度提高.

下面讨论一个3维的一篮子期权，它的收益函数为

利用主成分变换(12)式，收益函数变为

此时，可以构造如下的控制变量

为了比较不同控制变量之间的加速效果，考虑如下一些组合：

PCMC-1：用C₁做一元控制；

PCMC-2：用C₁，C₂做二元控制；

PCMC-3：用C₁，C₂，C₃做三元控制；

PCMC-4：用C²做一元控制；

PCMC-5：用C²，C₃做二元控制.

实际上，PCMC-1，PCMC-2，PCMC-3就是主成份蒙特卡罗方法2，PCMC-4是主成份蒙特卡罗方法1，PCMC-5是主成份蒙特卡罗方法3.

先讨论波动率对加速效果的影响.令

为了保证相关系数矩阵Γ的半正定性，必须有$-\frac{1}{2}≤ρ_{12}≤1. 取ρ_{12}=0.5，σ_{1}=σ_{2}=σ_{3}$，则协方差矩阵谱分解后特征值之比为 $λ_{1}:λ_{2}:λ_{3}=4:1:1.$改变波动率的大小，试验结果见表 3.

表 3再次验证实验1的结论.首先，固定特征值的比例时，波动率越大，方差减小指数越小.其次，从PCMC-1，PCMC-2，PCMC-3 3种方法来看，高维的多元控制变量比低维的多元控制变量效果要好.再次，比较PCMC-2和PCMC-4，发现后者的方差减小指数略大一些，尤其当波动率较大时.这是由于C²作为贴现收益函数的近似值时，比C₁，C₂的组合要准确一些.在PCMC-3和PCMC-5之间也有类似的结果.

改变特征值比例$\frac{λ_{1}}{λ_{2}}和\frac{λ_{1}}{λ_{3}}$的大小，下面比较各种控制变量方法的加速效果，结果见表 4. 表 4上半部分是固定$\frac{λ_{2}}{λ_{3}}=1:1$，可以看出方差减小指数随着波动率的减小而增大. 表 4的下半部分固定$\frac{λ_{1}}{λ_{2}}=4:1，$也有类似的结论.

亚式期权是一种典型的路径依赖期权，它的收益函数取决于标的资产在期权有效期内的平均表现.其定价问题也是一个多因子期权定价问题.亚式期权在到期日的收益分两大类：固定敲定价格或浮动敲定价格^[11].标的资产的平均表现可以是算术平均也可以是几何平均，即

考虑一个固定敲定价格的欧式看涨算术平均亚式期权，其在到期日的收益函数为

假设标的资产服从几何布朗运动，即

如果对时间作等距剖分，记$t_{j}=\frac{jT}{n}，j=0，1，…，n$.则标的资产在时间节点$t_{j}$处的价格为

其中：$S(0)$是初始股价，$r$是市场无风险利率，$σ$是波动率，向量$\boldsymbol{W}=(W(t_{1})，W(t_{2})，…，W(t_{n}))^{\text{T}}$定义了布朗运动的路径.显然，$\boldsymbol{W}$是一个正态随机向量，均值为零，协方差矩阵为

此时，期权定价问题即为求解

考虑一个具体的例子，到期日为T=1，n=32，则式(16)中的协方差矩阵Σ的特征值衰减得很快，最大的5个特征值分别是13.380 2，1.189 0，0.537 7，0.275 6和0.167 8，其累计贡献率分别是81%，90%，93%，95%及96%.这说明布朗路径的主要方差可以由前面少数几个主成分决定.对于一般情形，文献[12]分析了一般情形下布朗路径协方差矩阵的特征值的衰减规律.

对于欧式算数平均亚式期权，一般无法得到其封闭解.但容易得到其对应的几何平均亚式期权的价格^[13-14]，从而可以使用几何平均的亚式期权作为控制变量^[3].

下面讨论固定敲定价格的欧式看涨算术平均亚式期权的定价问题(17).令

针对不同控制变量方法的试验结果如表 5所示.其中k是满足累计贡献率ψ_k≥95%的主成分的最小个数. PCMC-1表示采用C₁作为一元控制变量，PCMC-2表示用C₁，C₂，…，C_k作为多元控制变量，PCMC-3表示使用所有的C₁，C₂，…，C_n作为多元控制变量. PCMC-4表示用C²，C₃，…，C_k作为多元控制变量，PCMC-5表示使用C²，C₃，…，C_n作为多元控制变量. GMC表示采用对应的几何平均亚式期权作为控制变量.

从表 5可以看出，对不同的观察点个数而言，各种控制变量方法的方差减小指数是比较稳定的.所有的多元PCMC方法都比GMC方法要好.如同我们在前面提过，(16)式中的协方差矩阵Σ的特征值衰减得很快，所以只需较小的k就会使得累计贡献率ψ_k很大.比如，当n=128时，前5个主成分就能解释95%的原始信息.

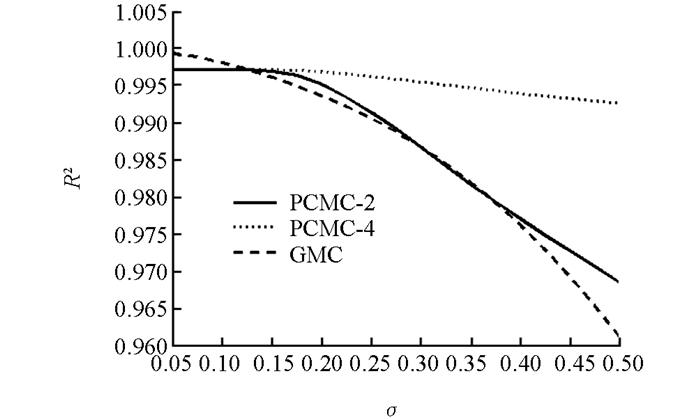
取n=32，k=8，考察波动率对方差减小效果的影响.不失一般性，主要考虑方法PCMC-2和PCMC-4.具体结果见图 1.显然，随着波动率的增加，各种控制变量方法的平方相关系数均下降.综合而言，我们提出的PCMC-4方法最稳定，具有最好的方差减小指数，尤其适合波动率较大的情况.

最后，考察不同到期日T的影响，见图 2.显然，GMC的平方相关系数随着到期日的增加下降最快，而我们提出的PCMC方法则相对十分稳定从而具有很好的加速效果.

在本文中，对于具有多个随机因子的欧式期权定价问题，基于标的资产状态变量的主成分变换构造了一系列的控制变量.数值结果说明，使用多个主成分控制变量方法可以大大提高蒙特卡罗模拟的效率，并且加速效果比较稳定.相对于使用几何平均的期权作为控制变量而言，本文提出的方法在各种参数下都具有更好的效果.

本文提出的通过主成分来构造控制变量的方法也可以推广到其它多因子定价模型，如高维的随机波动率模型以及随机利率模型下的衍生产品定价问题.