Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2017 Volume 39 Issue 4
Article Contents
Previous Article Next Article

Xu WANG, Xing LI. Numerical Solution of the Singular Integral Equation for the Problem of the Haversian Cortical Bone with a Radial Microcrack[J]. Journal of Southwest University Natural Science Edition, 2017, 39(4): 64-69. doi: 10.13718/j.cnki.xdzk.2017.04.010
Citation: Xu WANG, Xing LI. Numerical Solution of the Singular Integral Equation for the Problem of the Haversian Cortical Bone with a Radial Microcrack[J]. Journal of Southwest University Natural Science Edition, 2017, 39(4): 64-69. doi: 10.13718/j.cnki.xdzk.2017.04.010
shu

Numerical Solution of the Singular Integral Equation for the Problem of the Haversian Cortical Bone with a Radial Microcrack

  • 1.

    Institute of Ethnic Preparatory Education, Ningxia University, Yinchuan 750002, China

  • 2.

    School of Mathematics and Statistics, Ningxia University, Yinchuan 750021, China

More Information
  • Corresponding author: Xing LI
  • Received Date: 04/02/2015
    Available Online: 20/04/2017

  • MSC: O175.5

  • In this paper, the plane strain problem for the Haversian cortical bone with a radial microcrack in the interstitial bone under biaxial tension loading is considered. By using the singular integral equation method, the problem is formulated into a system of singular integral equations and the corresponding stress intensity factor is formulated. The effects of the material and the geometric parameters of the Haversian cortical bone upon the microcrack tip's stress intensity factor are numerically studied. The numerical results suggest that when the osteon is softer than the interstitial bone the osteon prompts the microcrack propagation, while when the osteon is stiffer than the interstitial bone the osteon repels microcrack propagation. However, this interaction effect is limited near the osteon.
  • 加载中
  • [1] FRATZL P, GUPTA H S, PASCHALIS E P, et al. Structure and Mechanical Quality of the Collagen-Mineral Nano-Composite in Bone [J]. Journal of Materials Chemistry, 2004, 14: 2115-2123. doi: 10.1039/B402005G

    CrossRef Google Scholar

    [2] FRATZL P, WEINKAMER R. Nature's Hierarchical Materials [J]. Progress in Materials Science, 2007, 52(8): 1263-1334. doi: 10.1016/j.pmatsci.2007.06.001

    CrossRef Google Scholar

    [3] HOGAN H A. Micromechanics Modeling of Haversian Cortical Bone Properties [J]. Journal of Biomechanics, 1992, 25(5): 549-556. doi: 10.1016/0021-9290(92)90095-I

    CrossRef Google Scholar

    [4] GUO X E, LIANG L C, GOLDSTEIN S A. Micromechanics of Osteonal Cortical Bone Fracture [J]. Journal of Biomechanical Engineerring, 1998, 120(1): 112-117. doi: 10.1115/1.2834290

    CrossRef Google Scholar

    [5] HOC T, HENRY L, VERDIER M, et al. Effect of Microstructure on the Mechanical Properties of Haversian Cortical Bone [J]. Bone, 2006, 38: 466-474. doi: 10.1016/j.bone.2005.09.017

    CrossRef Google Scholar

    [6] MEYERS M A, CHEN P Y, LIN A Y M, et al. Biological Materials: Structure and Mechanical Properties [J]. Progress in Materials Science, 2008, 53(1): 1-206. doi: 10.1016/j.pmatsci.2007.05.002

    CrossRef Google Scholar

    [7] TEMENOFF J S, MIKOS A G. 生物材料——生物学与材料科学的交叉[M]. 王远亮, 等, 译. 北京: 科学出版社, 2008.

    Google Scholar

    [8] ZIOUPOS P. Accumulation of in-Vivo Fatigue Microdamage and its Relation to Biomechanical Properties in Ageing Human Cortical Bone [J]. Journal of Microscopy, 2001, 201(2): 270-278. doi: 10.1046/j.1365-2818.2001.00783.x

    CrossRef Google Scholar

    [9] MOW V C, HUISKES R. 骨科生物力学暨力学生物学[M]. 汤亭亭, 裴国献, 李旭, 等, 译. 山东: 山东科学技术出版社, 2005.

    Google Scholar

    [10] NALLA R K, KRUZIC J J, KINNEY J H, et al. Effect of Aging on the Toughness of Human Cortical Bone: Evaluation by R-Curves [J]. Bone, 2004, 35(6): 1240-1246. doi: 10.1016/j.bone.2004.07.016

    CrossRef Google Scholar

    [11] O'BRIEN F J, TAYLOR D, LEE T C. The Effect of Bone Microstructure on the Initiation and Growth of Microcracks [J]. Journal of Orthopaedic Research, 2005, 23(2): 475-480. doi: 10.1016/j.orthres.2004.08.005

    CrossRef Google Scholar

    [12] MOHSIN S, O'BRIEN F J, LEE T C. Osteonal Crack Barriers in Ovine Compact Bone [J]. Journal of Anatomy, 2006, 208(1): 81-89. doi: 10.1111/joa.2006.208.issue-1

    CrossRef Google Scholar

    [13] NAJAFI A R, ARSHI A R, ESLAMI M R, et al. Micromechanics Fracture in Osteonal Cortical Bone: A Study of the Interactions Between Microcrack Propagation, Microstructure and the Material Properties [J]. Journal of Biomechanics, 2007, 40: 2788-2795. doi: 10.1016/j.jbiomech.2007.01.017

    CrossRef Google Scholar

    [14] NAJAFI A R, ARSHI A R, ESLAMI M R, et al. Haversian Cortical Bone Model with Many Radial Microcracks: An Elastic Analytic Solution [J]. Medical Engineering and Physics, 2007, 29(6): 708-717. doi: 10.1016/j.medengphy.2006.08.001

    CrossRef Google Scholar

    [15] NAJAFI A R, ARSHI A R, SAFFAR K P, et al. A Fiber-Ceramic Matrix Composite Material Model for Osteonal Cortical Bone Fracture Micromechanics: Soultion of Arbitrary Microcracks Interaction [J]. Journal of the Mechanical Behavior of Biomedical Materials, 2009, 2(3): 217-223. doi: 10.1016/j.jmbbm.2008.06.003

    CrossRef Google Scholar

    [16] HILLS D A, KELLY P A, DAI D N, et al. Solution of Crack Problems: the Distributed Dislocation Technique [M]. Dordrecht: Kluwer, 1996.

    Google Scholar

    [17] 李星.积分方程[M].北京:科学出版社, 2008.

    Google Scholar

    [18] XIAO Z M, CHEN B J. Stress Intensity Factor for a Griffith Crack Interacting with a Coated Inclusion [J]. International Journal of Fracture, 2001, 108: 193-205. doi: 10.1023/A:1011066521439

    CrossRef Google Scholar

    [19] MUSKHELISHVILI N I. Some Basic Problems of the Mathematical Theory of Elasticity [M]. Groningen Holland: P. NoordhoffLtd, 1953.

    Google Scholar

    [20] LI X, LI Z X. Effect of a Periodic Elastic Gasket on Periodic Cracks [J]. Engineering Fracture Mechanics, 1993, 46(1): 127-131. doi: 10.1016/0013-7944(93)90309-G

    CrossRef Google Scholar

    [21] XIAO Z M, CHEN B J. On the Interaction Between an Edge Dislocation and a Coated Inclusion [J]. International Journal of Solids and Structures, 2001, 38: 2533-2548. doi: 10.1016/S0020-7683(00)00169-4

    CrossRef Google Scholar

    [22] ERDOGAN F, GUPTA G D, RATWANI M. Interaction Between a Circular Inclusion and an Arbitrarily Oriented Crack [J]. Journal of Applied Mechanics, 1974, 41(4): 1007-1013. doi: 10.1115/1.3423424

    CrossRef Google Scholar

    [23] 徐芝纶.弹性力学简明教程[M]. 3版.北京:高等教育出版社, 2002.

    Google Scholar

    [24] O'BRIEN F J, TAYLOR D, LEET C. Bone as a Composite Material: The Role of Osteons as Barriers to Crack Growth in Compact Bone [J]. International Journal of Fatigue, 2007, 29: 1051-1056. doi: 10.1016/j.ijfatigue.2006.09.017

    CrossRef Google Scholar

    [25] 卢钰松, 王五生.一类含有p次幂的Volterra-Fredholm型非线性迭代积分不等式[J].西南大学学报(自然科学版), 2015, 37(8): 76-80.

    Google Scholar

    [26] 侯宗毅, 王五生.一类变下限非线性Volterra-Fredholm型积分不等式及其应用[J].西南师范大学学报(自然科学版), 2016, 41(2): 21-25.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(3)

Export Citation
PDF
XML

Article Metrics

Article views(859) PDF downloads(125) Cited by(0)

Access History

Other Articles By Authors

Numerical Solution of the Singular Integral Equation for the Problem of the Haversian Cortical Bone with a Radial Microcrack

    Corresponding author: Xing LI
  • Received Date: 04/02/2015
  • Available Online: 20/04/2017

Abstract: In this paper, the plane strain problem for the Haversian cortical bone with a radial microcrack in the interstitial bone under biaxial tension loading is considered. By using the singular integral equation method, the problem is formulated into a system of singular integral equations and the corresponding stress intensity factor is formulated. The effects of the material and the geometric parameters of the Haversian cortical bone upon the microcrack tip's stress intensity factor are numerically studied. The numerical results suggest that when the osteon is softer than the interstitial bone the osteon prompts the microcrack propagation, while when the osteon is stiffer than the interstitial bone the osteon repels microcrack propagation. However, this interaction effect is limited near the osteon.

    HTML

  • 文献[1-2]研究了骨头的分层结构，骨组织可分为密质骨和松质骨.哈弗氏密质骨由骨单位和间质骨组成.骨单位是由同心圆排列的骨板围成的长筒状结构，中心有一纵向的哈弗氏管，内含血管和神经.间质骨位于骨单位之间，形状不规则，是旧的骨单位在骨的改建过程中被吸收后残留的部分[3-4].由于哈弗氏管和骨单位的微观结构对密质骨力学性能有重要影响，因而模型考虑了这些微观结构.从微观结构和力学行为出发，哈弗氏密质骨与纤维涂层复合材料相似[5]：哈弗氏管与纤维类似，骨单位与涂层类似，间质骨与基类似，粘合线相当于界面.因而，可以将密质骨的分层结构与纤维涂层复合材料类比.

    文献[6-7]研究了骨的疲劳现象，这种现象在医学上被认为是应力断裂.由于日常运动的循环载荷，骨组织的微观损伤以微裂纹的形式表现出来[8-9].实验方法常用来研究骨单位的结构和断裂[10-12].骨的微结构有利于微裂纹的萌生[12]，但骨单位阻碍密质骨中微裂纹的扩展，这种作用还依赖于微裂纹的长度[11-12].计算机模拟，尤其是有限元方法已应用于密质骨断裂力学问题的研究.文献[13]利用有限元方法模拟了哈弗氏密质骨骨单位附近微裂纹的扩展.理论研究，尤其是奇异积分方程方法也应用于密质骨断裂力学问题的研究[4, 14-15].文献[4]研究了密质骨骨单位与单条微裂纹的相互作用，结果表明软骨单位有利于微裂纹的扩展，而硬骨单位阻碍微裂纹沿着骨单位扩展[4].文献[14-15]研究了多个微裂纹与骨单位的相互作用，结果表明这种相互作用仅局限在骨单位附近，同时也分析了不同形态下，微裂纹相互作用的增强和屏蔽作用.但是，理论上对哈弗氏密质骨间质骨含微裂纹问题还没有研究过，因而有必要利用奇异积分方程方法研究哈弗氏密质骨间质骨含微裂纹问题.

1.   模型描述

  • 如图 1所示，考虑了在骨单位附近，哈弗氏密质骨间质骨含单条径向微裂纹在无穷远处受双轴拉伸载荷σ0的平面应变问题.哈弗氏管位于骨单位中央，其半径为a，剪切模量为G1，常数K1=3-4v1.骨单位的厚度为b-a，其剪切模量为G2，常数K2=3-4v2.间质骨的剪切模量为G3，常数K3=3-4v3，其中v1，v2和v3是泊松比.

    基于线弹性断裂力学理论，将微裂纹看成是由连续分布的位错构成的，利用奇异积分方程方法，求出该模型所满足的奇异积分方程组.利用高斯切比雪夫求积公式[16-17]，对该方程组进行数值求解，讨论密质骨材料和几何参数对微裂纹尖端应力强度因子的影响.

2.   模型求解

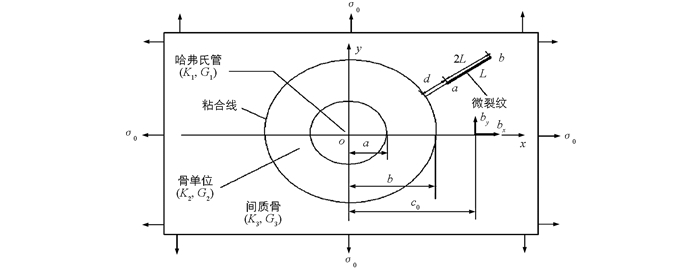
  • 如图 1，哈弗氏密质骨含径向微裂纹力学模型的求解可看成是以下两个基本问题A和B的叠加：

    问题A  哈弗氏管和骨单位镶嵌在间质骨中，间质骨不含微裂纹，哈弗氏密质骨含径向微裂纹力学模型的边界条件为

    问题B  考虑间质骨含径向直线微裂纹的应力分布问题.

    问题B里，外载荷只有微裂纹表面的牵引力，这个牵引力与问题A在虚裂纹位置的应力大小相等，方向相反.哈弗氏管、骨单位和间质骨界面的牵引力和位移连续条件为：

    其中τ=aeiθ，0≤θ≤2π.

    其中ζ=beiθ，0≤θ≤2π.

    • 2.1.   在直角坐标系下求解问题A的应力场

  • 问题A的应力场如下[18]：

    其中：

    • 2.2.   利用奇异积分方程方法求解问题B

  • 令间质骨在点(x，y)=(c0，0) 的位错贝格斯分量为bx和by.利用Muskhelishvili复变函数方法[19-20]，间质骨任一点P(x，y)的应力场如下：

    其中hxxx，hxxy，hyyx，hyyy，hxyx，hxyy的定义见文献[21]的附录.

    如果位错贝格斯分量bt和bn是L上的连续分布函数，bt沿着L，bn垂直于L，则问题B微裂纹上一点的切应力σt和正应力σn如下[22-23]：

    其中ht1，ht2，hn1和hn2如下：

    其中：

    (xc，yc)是微裂纹中点坐标.这里，m和n定义如下：

    其中，α是微裂纹与x轴的夹角.

    位移单值条件如下：

    分离位错密度函数的奇异性，bt(t0)和bn(t0)如下所示：

    其中，Ft(t0)和Fn(t0)是-1，1上的非奇异函数.

    将(27) 式和(28) 式代入(17)，(18)，(25) 和(26) 式，得：

    方程(29)-(32) 给出了哈弗氏密质骨骨单位附近间质骨含单条径向微裂纹问题的解.

    • 2.3.   径向直线微裂纹尖端应力强度因子

  • 径向直线微裂纹尖端的应力强度因子为[16]：

3.   数值结果

  • 当α=0时，数值算例考虑了哈弗氏密质骨含径向微裂纹受双轴拉伸载荷σ0.对于软骨单位，间质骨的剪切模量为G3=15 GPa；对于硬骨单位，间质骨的剪切模量为G3=10 GPa.哈弗氏管、骨单位和间质骨的泊松比分别为v1=v2=v3=0.3.无穷远处双轴拉伸载荷σ0=10 MPa.通过利用高斯切比雪夫求积公式，对奇异积分方程组(29)-(32) 进行数值求解[16-17]，讨论了微裂纹尖端应力强度因子随材料常数和几何参数的变化.

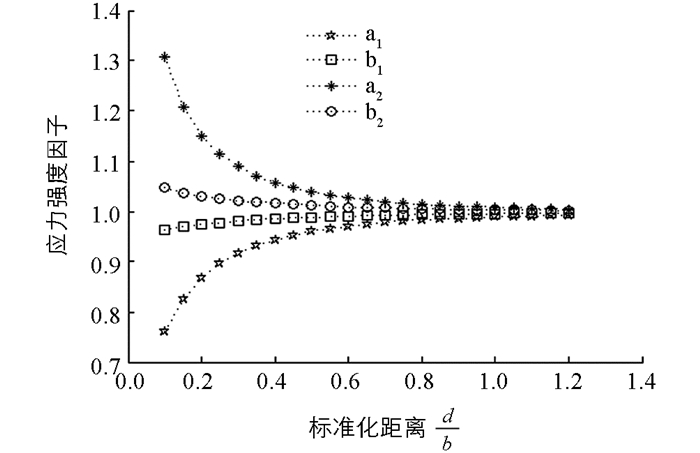
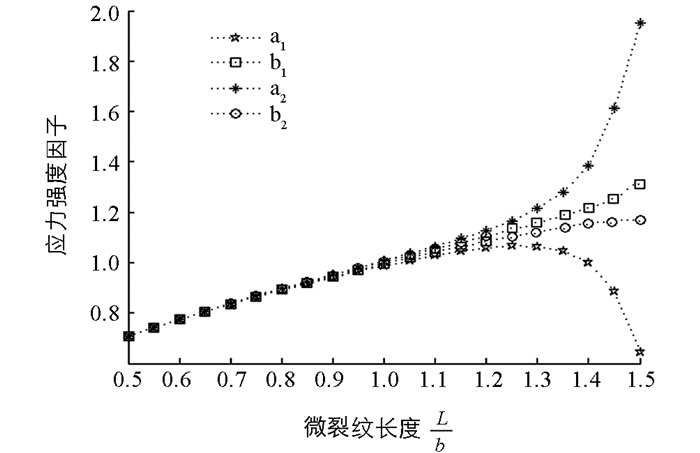
    假设骨单位的半径为b=100 μm，$ \frac{b}{a} $=1.5，微裂纹长度L=100 μm.如图 2所示，研究了不同剪切模量比下，微裂纹尖端(ai)和(bi)的标准化应力强度因子随标准化距离$ \frac{d}{b} $的变化.若$ \frac{{{G_1}}}{{{G_3}}} $=0.1，$ \frac{{{G_2}}}{{{G_3}}} $=0.005时，当微裂纹尖端(a1)无限接近骨单位时，微裂纹尖端(a1)的应力强度因子迅速增加，而微裂纹尖端(b1)的应力强度因子则缓慢增加，说明此时骨单位有利于微裂纹的扩展.若$ \frac{{{G_1}}}{{{G_3}}} $=10，$ \frac{{{G_2}}}{{{G_3}}} $=200时，当微裂纹尖端(a2)无限接近骨单位时，微裂纹尖端(a2)的应力强度因子急剧下降，而微裂纹尖端(b2)的应力强度因子则缓慢减少，说明此时骨单位对微裂纹具有屏蔽效应.但是，哈弗氏管和骨单位对微裂纹尖端应力强度因子的影响只局限在骨单位附近.上述数值结果与文献[13]用有限元方法得到的结果是一致的.

    如图 3所示，假设骨单位的半径b=100 μm，$ \frac{b}{a} $ =1.5，微裂纹尖端(b)固定.研究了不同剪切模量比下，微裂纹尖端(ai)和(bi)的应力强度因子随微裂纹长度$ \frac{L}{b} $的变化.当0.5≤$ \frac{L}{b} $ ≤1.2时，微裂纹尖端(ai)和(bi)的应力强度因子随微裂纹长度的增加而增加.若剪切模量比$ \frac{{{G_1}}}{{{G_3}}} $ =0.1，$ \frac{{{G_2}}}{{{G_3}}} $ =0.05时，则当微裂纹尖端(a1)接近骨单位时，微裂纹尖端(a1)和(b1)的应力强度因子迅速增加，而微裂纹尖端(a1)的应力强度因子增长更快，说明骨单位对微裂纹尖端(a1)的应力强度因子的影响更大.此时，微裂纹更容易在粘合线附近扩展.若剪切模量比$ \frac{{{G_1}}}{{{G_3}}} $ =10，$ \frac{{{G_2}}}{{{G_3}}} $ =20时，则当微裂纹尖端(a2)接近骨单位时，微裂纹尖端(a2)和(b2)的应力强度因子急剧减少，而微裂纹尖端(a2)的应力强度因子减少更快，说明骨单位对微裂纹尖端(a2)的应力强度因子的影响更大，这是因为微裂纹尖端(a2)距离骨单位更近的缘故.此时，骨单位对裂纹具有屏蔽效应.这与已有实验方法[24]得到的结果是一致的.另外也给出了一些预测结果，这些结果需要通过实验或有限元模拟来进一步验证.总的来说，不管是对于软骨单位还是硬骨单位，微裂纹与骨单位的相互作用仅局限在骨单位附近.

Figure (3)  Reference (26)

Catalog

    Copyright Journal of Southwest University Natural Science Edition

    Address： Tel：023-68254576, 68252540, 68366165,68366917 E-mail：lkxb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return