-
出行成本是交通出行者进行交通决策分析的重要依据,便宜且便捷的交通出行方式能够激励出行人更多采用该种出行方式,但是,交通事故风险成本作为出行成本的重要组成部分往往很容易被人忽略.据笔者在2012-2013年春运期间对摩托车返乡潮现象进行了探索性调查研究发现:骑车人普遍对出行成本概念存在严重的误解,其中71.76%的人认为骑车返乡成本只有车油费和伙食费;14.04%的人仅考虑油费;12.94%的人仅考虑油费、伙食费、维修费、住宿费;1.26%的人仅考虑油费和维修费.正是因为出行者对出行成本产生如此误解,认为摩托车方式返乡“便宜且便捷”的心理激励沿海务工人员更多采取摩托车这种高风险、低效率出行方式.
由此看出,忽略交通事故风险成本将导致对出行成本严重的误判.因此,有必要对交通事故风险成本进行科学的定量研究,为交通出行者的出行决策分析提供理论依据.公认的交通事故风险成本计算方法[1]是交通事故风险概率乘以相应的交通事故损失成本.目前,交通事故损失成本的定量已存在较为成熟的统计方法,因此,交通事故风险成本的研究关键在于如何科学定量交通事故风险,对于交通事故风险的研究,国内外许多专家学者已经取得丰硕成果.国外学者El-Basyouny[2]通过研究冲突与交通事故潜在关系,利用交通量以及相关的变量建立两阶段模型. Persaud Bhagwant等[3]采用各种安全参数,建立神经网络模型.此外还有Yannis George等[4]通过数据分析,建立死亡率与机动化水平相关的非线性模型.国内研究中,徐培培等[5]在量化交通出行成本同时提出交通风险认知度的构建.陈富坚等[6]将系统可靠性模型应用于道路交通系统事故风险模型的构建,从人、车、路、环境等要素分析对交通事故风险的影响.陈雪梅等[7]通过问卷调查等方式获得驾驶员的特征参数,利用BP神经网络分析技术,对驾驶员因素与交通事故风险二者之间内在关联性进行深入的研究.付锐等[8]通过采集路段事故数据以及纵断面线形参数,通过回归分析获得事故风险与纵断面参数相关关系.郭应时等[9]统计山区公路的交通事故风险数据与平面线形数据,采用角度变化率作为平面线形的表征参数,对样本路段区间内的事故风险与角度变化率进行回归分析,得出平面要素与事故风险的联系.
但是,现有的交通事故风险计算模型大多缺乏系统性考虑,或者简单将交通事故风险视为一个静态指标进行计算,因此,计算结果存在较大误差.对于实际道路交通,尤其是公路交通,是涉及人的行为与自然环境的复杂系统,在道路交通的运行过程中,系统状态随着时空推移而改变,事故风险也将随着时空推移而改变.因此,交通事故风险计算应紧扣交通系统性、事故风险的时变性.
本文通过系统分析方法对交通安全要素进行结构分析,探讨系统各要素间的相互作用,拟建立动态交通事故风险模型,并结合广义成本论,建立具有较强系统性、适应性的交通事故风险成本的计算方法.该模型更加全面地揭示了出行成本,为出行者的出行决策提供实际理论依据,而且从工程角度指导交通设计与管理,从人、车、路、环境的各角度缓解或减少交通事故的发生.
HTML
-
由引言分析可知,交通事故风险成本研究的关键是在于交通事故风险模型的构建,而交通事故风险研究应紧扣交通的系统性与事故风险的时变性.因此,有必要对影响交通事故风险的系统各要素进行系统结构分析,明确系统各要素之间相互关系,在各要素中选取关键要素建立交通事故风险模型.
-
1) 将交通风险系统要素分为人为要素、车辆要素、道路要素、环境要素,分别以S1,S2,S3,S4表征交通风险要素,则其系统要素表即要素集合为S=(S1 S2 S3 S4).
2) 根据系统各要素之间关系建立直接关系矩阵,若要素间有直接关系为1,若无直接关系即为0,则直接关系矩阵如下所示:
3) 将直接关系矩阵按照布尔运算规则计算得可达矩阵,可达矩阵不仅能够反映各要素之间的直接关系,且反映了系统中各要素之间的间接关系,T=Mn+1.
式中n为直接关系矩阵M的阶数,当T=M2=…=Mn+1时,停止计算得到可达矩阵如下所示:
可达矩阵能够反映系统总体结构,由可达矩阵得:人为要素能直接影响车辆要素,道路要素可通过直接作用于人为因素或车辆要素,进而影响交通事故风险,而道路要素仅受到环境要素直接影响,环境要素可直接影响所有其他要素而改变系统的事故风险,而仅受本身变化影响.为了更加直观划分各要素的相互关系,将可达矩阵分解成两个集合:
母集合R(Si):包含一切Si能到达的一切有关系的要素集合.如人为要素S1所能达到或影响的要素集合为车辆要素与其本身,集合形式为:(S1,S2).
子集合A(Si):包含一切有关系要素可以达到Si的要素集合.如环境变化会直接影响驾驶员操作造成事故风险增加,故人为要素S1能受环境要素(S4)直接影响.此外,人为要素(S1)还受道路要素(S3)直接影响,所以子集合为:(S1,S3,S4).进一步对系统结构进行层次分析,结果如表 1.
从表 1计算母集合与子集合的交集来判定上层要素,即是否满足R(Si)A(Si)=R(Si),若满足判别式,即为上层要素.车辆要素(S2)为系统最上层要素,去掉最上层要素,继续利用R(Si)A(Si)=R(Si),判定人为要素为二层要素,重复上述步骤,道路要素为三层要素.最后得环境因素为最下层要素.
由此可知,环境要素(S4)自身改变能够直接影响所有上层要素,道路要素(S3)能够直接影响车辆要素(S2)与人为要素(S1),人为要素(S1)受到道路要素(S3)、环境要素(S4)的直接影响,而车辆要素能被所有的其他要素直接影响,如图 1所示.
1.1. 交通风险要素分析
-
交通事故造成的损失一般分为当事人的损失,警察、法院等社会公共支出的费用,以及因交通阻塞等造成的第三者的损失等.根据我国习惯,后两项一般归入交通外部成本,而将出行者的个人损失作为交通事故损失,因此,本研究也遵循此惯例.
-
对于交通事故风险描述,车辆的交通事故率是必不可少的指标.而且通过系统结构分析得到车辆要素为系统最上层要素,各系统要素可直接作用车辆要素影响交通事故风险的变化.对于交通系统所有要素而言,车辆要素的事故率是整合所有系统要素关键所在.因此,本文重点以车辆要素为关键,将其他系统要素定义为动态影像因素,将各系统要素之间的关系看作是串联关系,建立相应的交通事故风险模型.从交通系统中人、路、环境等其他要素提取动态参数构建动态交通事故模型,分析各系统状态随时空变化对交通事故风险的影响.
由于不同出行方式的行驶稳定性以及安全性能具有较大差异,因此,不同出行方式所承担的交通事故风险必然存在不同,其最重要的体现就在各出行方式之间交通事故数量上以及事故严重程度的不同,因此,建立基本交通事故风险时,通过聚类分析法按不同的车型以及事故严重程度进行建模.
-
交通事故的发生具有偶然性,导致交通事故发生的原因众多,而车辆因素也只是引发交通事故原因之一,所以在统计期内交通事故分布具有一定的离散性.为了消除交通事故的偶然性和其他因素的影响,一般以12月为统计步长对同一出行方式的交通事故数据进行统计计算,则各出行方式的交通事故风险计算模型如下所示:
式(1)中Pij为单元路段内交通方式i的特定j类型事故的年平均基本事故率;qij为单位时长区间单元路段内交通方式i的特定j类型事故的基本事故总数;Qj为单位时长区间内单元路段内特定j类型机动车交通量.
-
在第一章的分析中,通过结构分析可知,交通系统的其他要素,如人为要素、道路要素、环境要素均能通过一定的结构,彼此之间相互作用对车辆要素的交通事故风险产生重要的影响,因此,动态风险模型可通过串联模型建立.同时、建模时还应考虑交通系统的其他要素都能具有较强的时变性,当其他要素变化时,能够影响车辆要素,改变系统整体风险.因此,需要考虑系统要素随着时间、空间的推移而不断变化,导致交通事故风险的变化,进而影响事故风险成本,模型如下所示:
上式中,Pij为单元路段内实际地交通事故风险概率;pij为单元路段内交通方式i的特定j类型事故的平均基本事故率;αh为驾驶员影响系数;αr为道路影响系数;αe为环境影响系数;t为时间变量;l为空间(行程)变量.
-
交通事故成本可分解为财产等物质损耗、身体损伤等身体损耗甚至包括生命损耗成本.考虑到交通事故严重程度不同,所担负的成本存在较大差异,故建模时需要分别考虑不同交通事故类型所承担的经济损失.为了减少计算误差,将交通事故类型划分为三类计算,轻微事故(Q1):仅存在财产损失的交通事故类型;普通事故(Q2):存在人员受伤且伴随财产损失交通事故;致命事故(Q3):有人员死亡且伴随严重财产损失的交通事故.
式3中,Pij为单元路段内交通方式i的特定j类型的实际交通事故风险概率(次/辆);Cj为单元路段内特定j类型事故的对应损失成本;j=1,2,3分别表示轻微交通事故,普通交通事故,致死交通事故.
2.1. 建模思想
2.2. 经验风险模型
2.3. 动态风险模型
2.4. 交通事故风险成本模型
-
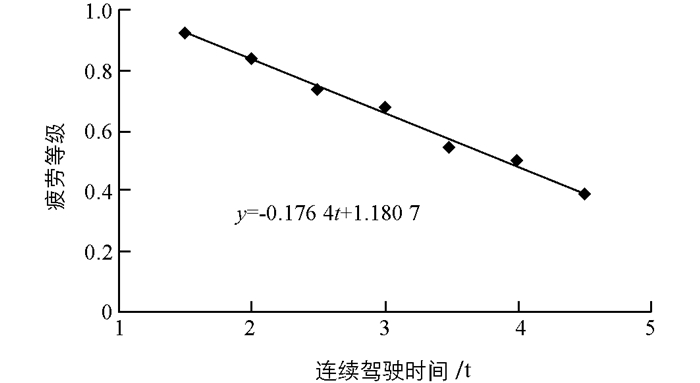
人为因素是事故分析的主要对象,因为驾驶员的驾驶行为会直接影响交通安全风险.国内外的交通事故统计表明,有80%~90%的交通事故是由人的因素造成的,其中文献[10-11]对交通事故致因中的人为因素分析发现:超速驾驶行驶与疲劳驾驶是最主要的两个人为因素,而驾驶疲劳导致感知迟钝、判断不准、操作失误在事故中占了绝大多数.因此,马艳丽等[12]为了获得驾驶疲劳和驾驶时间量化关系,进行了大量的实验研究,为了提高驾驶疲劳的评价精度,引入深度知觉、速度知觉、反应时间、误操作等指标以模糊聚类方法对驾驶员的疲劳程度进行了较为科学的评估,其研究结果如下.
表 2数据是经过大量的实验研究获得,其中的统计数据是非疲劳状态的隶属度,这意味着数字越大,疲劳程度越小.基于表 2,采用回归分析获得回归模型,如图 2所示,驾驶疲劳与连续驾驶时间成正相关,以疲劳隶属度最小的1.5 h连续行驶时间为理想行驶时间,超过理想时间则风险将会越来越大,所以1.5 h连续行驶时间的隶属度被视为驾驶风险的基准值,疲劳影响系数αf(t)定义为基准值的隶属度比连续行驶时间大于1.5 h相应隶属度,公式表达如下:
此外,超速行驶是导致交通事故发生的另一重要的人为因素.速度越高、驾驶员反应时间越少,增加制动距离,同时使得碰撞时释放的能量增大,因此,速度能够较好地说明车辆行驶状态[10].故澳大利亚RTA[13]研究速度与事故危险性的关系,如表 3所示.该研究以60 km/h的行驶速度的行车风险作为基准值,通过与基准值对比分析确认各车速之间相对危险性,因此,该表能较好反映速度对交通风险的影响.
-
道路几何线形要素构成是否合理,对交通安全有较大影响.对实际交通环境而言,道路属性是随着时空变化的,即道路的曲率与坡度等指标是随时空变化的,所以事故风险也随着时空变化的.其中有研究通过调查分析[14],揭示纵坡坡度以及曲率均对事故概率有显著影响,由于纵坡与曲率事故机理是不一样的,故可将两个因素视为相互独立事件,独立考虑纵坡、曲率对事故率的影响.通过数据对比分析,纵坡与曲率都与事故成正相关,以最小纵坡事故率、最小曲率事故率作为基准值,那么其它纵坡坡度以及曲率的事故率与基准值的比值,可较好反映坡度与曲率的交通事故风险影响,如表 4、表 5.
-
行车环境与交通事故有着密切的关系.据张利等[15]通过对有关雨雪天气的安全行车调查研究中发现,路面湿滑是雨雪天气的事故率明显高于晴天事故率的重要原因,交通事故风险需要考虑行车环境的影响[16].据美国宾夕法尼亚州交通部门的调查研究[17],得出路面状况和汽车交通事故率的关系,而路面状况的不同是由不同天气所造成的,以此推导出天气与事故率的关系.由理想天气下事故率作为基准,对系数进行标定,如表 6所示.
3.1. 人为因素分析
3.2. 道路影响分析
3.3. 环境影响分析
-
交通事故风险成本的研究主要是为了合理定量出行成本,为出行者的出行决策提供合理的理论依据,因此,案例主要以客运交通的事故风险成本进行探讨,下面以珠海某一级公路的实际的数据为例说明交通事故风险成本计算模型的实际应用.
1) 道路分析说明.该路段为珠海的干道公路,双向8车道,设计时速为60 km/h,长约5.42 km,地形条件良好,仅有4个平曲线且最小平曲线半径有380 m.再者,竖曲线最大纵坡为2.143%,无弯坡组合.
2) 各出行方式的通行交通量获取.据交警部门统计资料得出,该路段通行交通量较大,年平均日交通量为90 025车次,其中小汽车交通量约占机动车73%,摩托车交通量约占机动车5%,大型客车约占机动车10%,货车类交通量约占机动车12%.因为事故风险成本将讨论客运交通的出行成本,故货车类的事故风险成本在此不予考虑.
3) 统计各客运出行方式的基础交通事故率.对24个月统计期内的交通事故数据分析,发现交通事故主要对象是小汽车事故、摩托车事故,大型客车的事故极少,在整个统计区间内仅有一例交通事故,故不予讨论,即交通事故风险的讨论将以小汽车与摩托车为讨论对象.其中该路段每年平均发生12起交通事故,其中摩托车致死交通事故约为3起,普通交通事故约为3起,小汽车平均发生普通事故约为6起,普通事故约为4起,致死事故约为2起.
4) 交通事故风险参数的标定.交通事故风险成本研究是为了为个体出行决策提供理论依据,因此,交通事故风险成本的计算应该针对个体出行者.车辆行进过程中,驾驶员连续行驶时间、行驶速度、行驶空间、乃至天气条件都不尽相同,所以不同出行者所承担的交通事故风险必然存在差异.故本文通过假设对各因素进行讨论,通过假设,对比理想条件与极端状态的条件下,交通事故风险成本的差别,计算结果如表 7所示.
-
本文以车辆要素为建模的关键,通过聚类分析建立交通事故风险基本模型,通过提取连续行驶时间、车速、曲率、道路纵坡以及天气等动态参数构建动态的交通事故风险成本模型,并用珠海某干道公路交通数据进行应用分析,其结论如下:
1) 通过对比分析得,不同出行方式的交通事故风险成本差异较大,合理选择交通出行方式可有效降低交通事故风险成本及出行成本.算例结果表明:弱势出行方式,特别是摩托车,属于高风险、高成本的出行方式,需对弱势出行方式进行有效的管理控制,如将弱势交通方式与较为强势的交通方式进行空间分离以及速度控制等管理,能有效降低事故风险成本.
2) 本文构建的事故风险成本模型能够兼顾交通事故风险的系统性与时变性,能够比较全面有效地从交通系统人、车、路、环境4个角度反映交通事故风险形成机理,且动态交通事故风险成本能直观反映实际的交通事故风险,不仅能为出行者的出行决策提供实际应用分析,而且能从工程角度指导交通设计与管理,缓解或减少交通事故的发生.







 DownLoad:
DownLoad: