-
随着经济水平的不断提高,国民拥有的汽车数量也在与日俱增,随之而来的问题是对石油资源的需求量越来越大,汽车排放的尾气对大气污染也日趋严重,与此同时,我国还有大量的农用机械发动机和发电用发动机,能源问题和环境问题已经成为一个亟待解决的难题.大量研究表明,当发动机的空气和燃油比处于理论空燃比A/F=14.7(定义此时的过量空气系数λ=1)附近时,三元催化器对燃油燃烧产生的有害气体的转换效率达到最大,此时发动机动力达到最大,尾气排放性最好,具有较好的燃油经济性.发动机空燃比控制的主要难点在于:发动机系统是一个高度非线性、时变性的系统,在工作过程中许多参数与外部环境变化息息相关,而使用传统的PID控制由比例、积分、微分3个环节的线性调节系统对发动机空燃比进行控制时,很难取得高精度控制效果[1-4].
针对发动机系统的非线性时变性问题,本文提出一种基于蝙蝠算法整定参数的PID控制方法,并结合油膜补偿模型,建立更优的空燃比控制系统模型.
HTML
-
蝙蝠算法(Bat Algorithm,BA)是一种启发式寻优算法,由Xin-Shen Yang教授于2012年首次提出[5].现实生活中蝙蝠通过超声波来确定物体的信息,在此基础上演化出了蝙蝠算法,它是一种基于迭代的优化算法[6-7].首先在可行空间里任意初始化一组随机解,然后通过迭代算法搜寻最优解,并且在最优解周围生成随机的新解来增强局部搜索,从而精确掌握目标的空间位置.
-
根据蝙蝠觅食的过程,蝙蝠的速度、频率和坐标位置可由如下式子表示:
式中,β∈[0, 1]的随机数,fmin,fmax为频率f的范围,xbest为第t时刻的全局最优解.
在可行空间内的蝙蝠,一旦确定当前最优解,每只蝙蝠会做一次随机运动,从而产生一组新的解,新的位置用如下式子表示:
式中,ε∈[-1, 1]的随机数,At是整个蝙蝠族群的脉冲强度在t时刻的平均值.
-
研究表明,蝙蝠最初搜寻时,发出脉冲强度较大的超声波脉冲,实现大范围搜索,当蝙蝠接近猎物时,会减弱发出超声波脉冲的强度,并且增加发射频率,以实现精确定位.每只蝙蝠发出的超声波脉冲强度和频率随着算法的迭代不断更新,用以下公式模拟这一过程:
其中,0<α<1,γ>0;当t→∞时,Ait→0,rit→ri0.
1.1. 位置更新
1.2. 脉冲强度和频率
-
目标函数是评定一个系统性能的指标.对于PID控制系统的3个控制参数,比例控制(P)单元会使系统产生稳态误差;积分控制(I)单元可消除稳态误差,但可能会增加超调;微分控制(D)单元可以加快系统的响应速度以及减弱超调趋势[8].由此可见,3个控制单元的性能指标往往是相互矛盾的,因此很难要求所有指标都取得最优值.我们选用基于积分误差函数作为评定PID控制系统性能的指标,积分误差函数常用的有:绝对误差积分IAE,时间乘绝对误差积分ITAE,平方误差积分ISE,时间乘平方误差积分ITSE[9].其中ISE和IAE没有时间约束,能在最短的时间内就能使系统单位阶跃响应达到稳态值,但是相应地容易引起较大的超调.这里,我们以ITSE作为目标函数,其表达式如下.
为了便于计算,这里选取积分限为[0,ts],其中ts为调节时间.对积分限进行离散,取采样周期为T,用一系列采样点kT代替连续时间ts,进行离散化,得到ITSE的离散化公式.
其中,N=ts/T.
基于蝙蝠算法的PID参数整定是旨在寻优空间Kp∈[Kpmin,Kpmax],Ki∈[Kimian,Kimax],Kd∈[Kdmin,Kdmax]中,寻找一组最优的(Kp,Ki,Kd),使得PID控制器产生的单位阶跃信号的ITSE值最小.
-
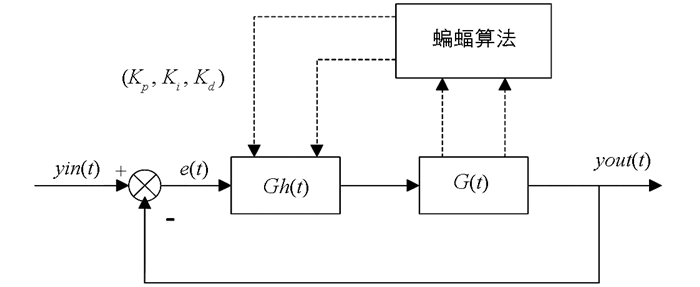
基于蝙蝠算法的PID参数整定的框图如图 1所示.
根据被控对象的传递函数,对于PID控制器的3个参数进行蝙蝠算法迭代计算,每一次更新的蝙蝠的速度、频率和位置对应每一组PID参数的比例控制单元、积分控制单元和微分控制单元,以此建立闭环控制系统.然后根据闭环控制产生的单位阶跃响应计算系统的ITSE积分误差,可以获得一组使得ITSE值最小的PID参数.
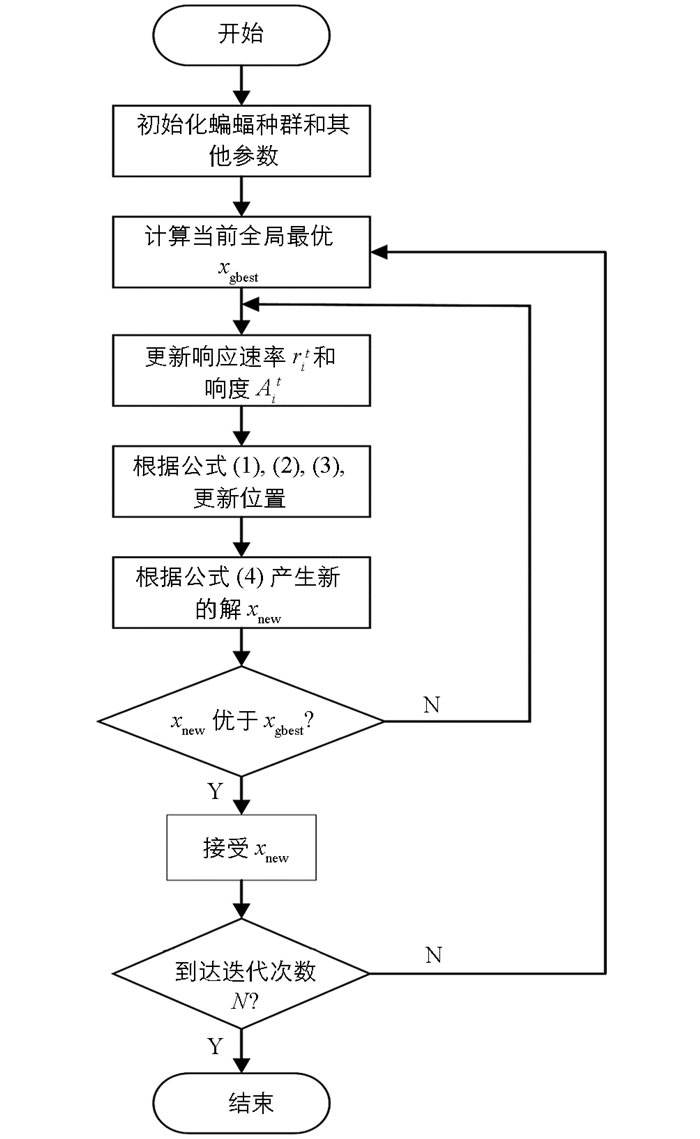
对于每一周期的算法迭代,算法首先会对每个个体进行全局寻优,得出全局寻优解,然后根据公式(1)、(2)、(3)更新蝙蝠的速度、频率和位置,对于每一个蝙蝠个体,根据位置更新,算法会进行局部寻优,如果得出局部寻优的最新位置优于全局寻优,则会更新这只蝙蝠的位置,否则保持原先位置.整个算法流程图如图 2所示.
2.1. 目标函数的选取
2.2. PID参数的整定
-
为了使PID控制器在发动机设计上运用,需要对发动机建立仿真模型,先把控制器运用到仿真模型中进行仿真测试.目前使用最广泛的物理分析模型有计算流体力学模型和平均值模型,计算流体力学模型致力于描述发动机的流体力学特性,是最复杂也是能最详尽描述发动机流体动力学特性的模型,但是建模过程复杂,需要对庞大的数据进行微分方程求解,计算量大,很难满足发动机控制系统的实时性需求.发动机平均值模型忽略发动机不同的曲轴转角所对应的缸内变化,只是对发动机的单个工作循环进行研究,对缸内的工作状态进行平均化处理,它可以对发动机工作过程的稳态和瞬态工况都能很好地描述[10].
-
影响发动机瞬态工况下空燃比波动较大的主要原因之一是油膜动态效应,即进气道管壁面油膜附着、蒸发的动态过程,因此有必要对油膜进行补偿.目前对油膜动态过程建模采用最多的是x-τ油膜模型来描述进气道油膜现象,其表达式如下:
其中,$\dot{m}_{f f}$为油膜质量流量变化量,$\dot{m}_{f i}$为喷油器喷出的燃油质量流量,mff为油膜质量流量,$\dot{m}_{f e}$为实际进入气缸的燃油质量流量,x为喷射的燃油附壁比例,τ为油膜质量蒸发时间常数.对上式进行Laplace变换,得到油膜模型传递函数:
对油膜进行补偿,则理想的补偿器传递函数应为油膜模型传递函数的逆函数,应为
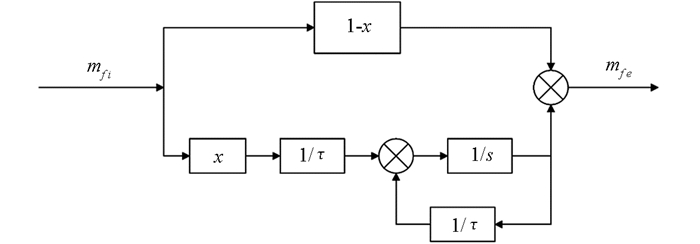
从上式可以发现,油膜补偿模型的建立跟燃油附壁比例x和油膜质量蒸发时间常数τ这两个时变非线性参数相关[11].采用Elman神经网络对油膜参数(x,τ)进行识别[12-14],油膜补偿模型的控制框图如图 3所示.
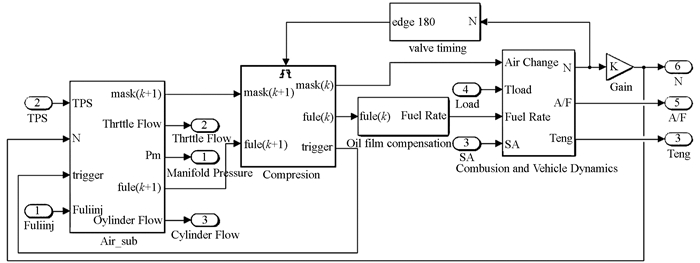
本文以某款125cc单缸机为研究对象,建立发动机平均值模型,包括空气效率模型、燃油喷射模型、油膜补偿模型、动力输出模型,该模型是一种既可以描述发动机稳态工况也可以描述瞬态变化的物理过程,如图 4所示.
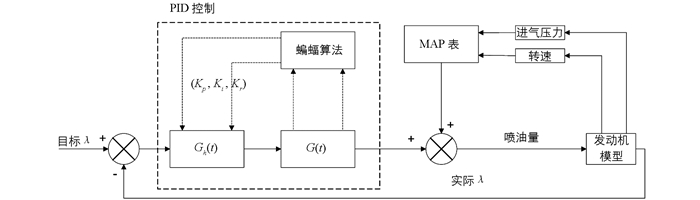
发动机系统是一个高度非线性时变系统,这对于控制系统提出了很高的要求,本文采用基于蝙蝠算法整定PID参数的控制系统,解决了传统PID控制对于非线性时变系统难以取得精确控制的问题,其控制框图如图 5所示.整个控制系统分为开环控制和闭环控制两个部分共同调节,其中开环控制通过获取发动机运行时的进气压力和转速,并结合MAP图可以计算出基本喷油量;闭环控制通过实际空燃比反馈回PID控制器对喷油量进行精确调节,通过控制喷油嘴的喷油量来对空燃比进行控制.
-
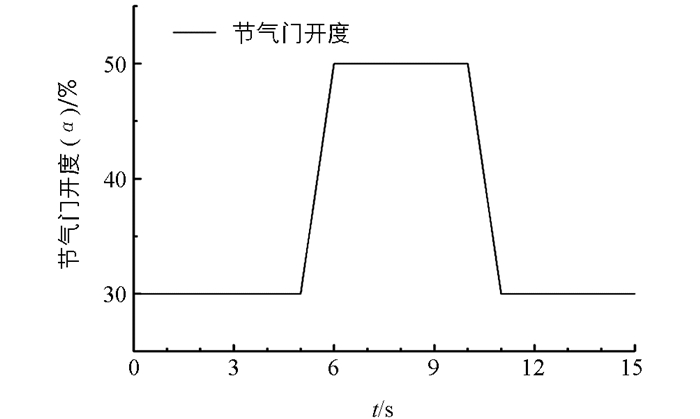
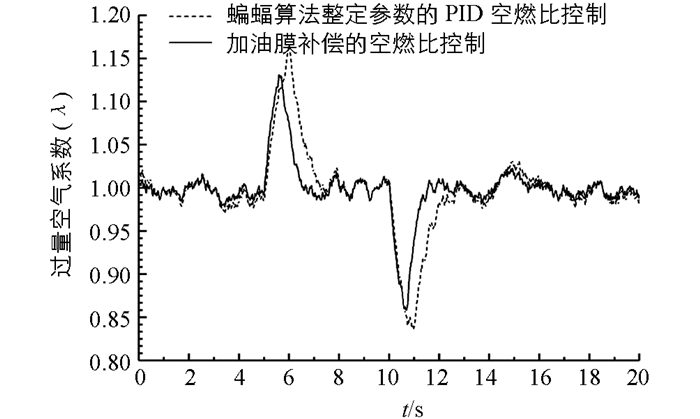
为了验证本文提出的基于蝙蝠算法整定参数的PID控制器的有效性,在发动机运行过程中改变节气门开度,以此来控制空燃比的动态响应曲线,对比不同的控制下的空燃比响应曲线. 图 6表示在1 s内节气门开度瞬时增大和减小的情况下,仿真得到的过量空气系数变化曲线如图 7所示.从仿真曲线图可以看出,当节气门开度瞬时增大和减小时,普通PID控制器大约会在2.5 s之后使过量空气系数λ维持稳定在1左右,而基于蝙蝠算法整定参数的PID控制器大约只需要2 s左右的时间.而且基于蝙蝠算法整定参数的PID控制的空燃比系数在节气门开度变化时的波动范围普遍降低0.05左右,基于蝙蝠算法整定参数的PID控制策略相比于普通的PID控制能更快地使过量空气系数维持在理论空燃比附近.
加入油膜补偿后的仿真图形如图 8所示,从仿真波形可以看出,加入油膜补偿模型的发动机空燃比控制相较于只用基于蝙蝠算法整定参数的PID控制器的空燃比控制模型波动变小,当节气门开度瞬间变化时,加入油膜补偿模型的过量空燃比系数的波动幅度降低32%左右,达到稳态的时间也减少了0.5 s左右.当节气门开度维持不变的情况下,加入了油膜补偿模型的空燃比控制系统对于降低随机波动信号对于空燃比的影响也具有较好的效果.
3.1. 油膜补偿模型
3.2. 仿真结果与分析
-
本文将一种群体算法蝙蝠算法应用到传统PID控制器中,将改进后的蝙蝠算法整定参数的PID控制策略应用到某款125cc单缸发动机的平均值模型中,对发动机瞬态工况下的空燃比进行控制.当节气门突变时,基于蝙蝠算法整定参数的PID控制器维持空燃比稳定在理论空燃比附近所需要的时间相对于普通PID控制器所需要的时间要少0.5 s左右,并且加入了蝙蝠算法的PID控制器对于空燃比的波动范围有明显降低.在发动机平均值模型中加入油膜补偿模型后,维持空燃比稳定所需的时间进一步减小,波动范围也进一步降低了32%左右.仿真结果表明,该蝙蝠算法整定参数的PID控制器能够很好地适应发动机模型的非线性和时变特性,在过渡情况下能明显改善对空燃比的控制效果,在对发动机空燃比的控制过程中具有良好的鲁棒性.







 DownLoad:
DownLoad: