-
据世界卫生组织统计,至2017年底全球约有3 690万艾滋病毒携带者,同年有94万人死于艾滋病毒相关病症,艾滋病毒的传播仍是一项属于全球主要公共卫生问题[1].艾滋病毒(HIV)主要攻击人体免疫系统从而导致免疫功能的丧失,其中CD4+T细胞是重点攻击对象.美国食品和药物管理局已认定20多种抗HIV药物,这些药物主要分为两类,逆转录酶抑制剂(RTIs)和蛋白酶抑制剂(PIs)[2].如今,抗逆转录病毒药物能够有效控制HIV感染者的病情,但未提高感染者自身免疫力,最终感染者可能由于自身免疫力较弱而死于其他类型疾病.近年来,HIV免疫治疗法的采用可有效增强HIV感染者的自身免疫力[2-3].
文献[3]首先提出一类考虑免疫治疗因素的CD4+T细胞和游离病毒相互作用的HIV进展模型,文献[4]再将抑制病毒输入的治疗因素引入该模型,得到如下模型
其中:T=T(t)表示t时刻血浆中CD4+T细胞的浓度,V=V(t)表示t时刻血浆中游离病毒的浓度,s1为CD4+T细胞的增殖率,
$\frac{{{s_2}V\left( t \right)}}{{{b_1} + V\left( t \right)}}$ 为游离病毒对CD4+T细胞增殖的抑制率,$\frac{{gV\left( t \right)}}{{{b_2} + V\left( t \right)}}$ 为血浆中来源于淋巴系统和CD4+T细胞的游离病毒输入率,μ1为CD4+T细胞的死亡率,k为游离病毒对CD4+T细胞的感染率,c为CD4+T细胞对游离病毒的杀伤率,u1表示细胞因子(白细胞介素Interleukin-2,简写为IL-2)激活CD4+T细胞的速率系数,u2表示抑制病毒的治疗策略.由于IL-2具有激活和分化T淋巴细胞以获得增殖的作用[3],因此在免疫治疗过程中,IL-2是通过皮下注射于HIV感染者体内,然后在体内激活、分化CD4+T细胞,促进其增殖.在文献[5]的免疫治疗模型中引入感染者体内免疫治疗药物IL-2浓度变化的微分方程
其中:I=I(t)表示t时刻血浆中免疫治疗药物IL-2的浓度,μI为免疫治疗药物IL-2的衰减率,VI(t)为t时刻皮下注射IL-2的速度.注意到游离病毒存在自然死亡这一客观事实,本文将在模型(1)和模型(2)的基础上,考虑如下模型
其中:a为免疫治疗药物IL-2对CD4+T细胞的激活率,μ2为游离病毒的自然死亡率,其余参数的生物学意义同模型(1)和(2).系统(3)中参数s1,s2,b1,b2,μ1,μ2,k,a,g,c,μI均为正数.
本文将以皮下注射IL-2的速度VI(t)为控制变量,以实现CD4+T细胞浓度较大而IL-2注射速度较小为目标,建立治疗HIV的最优控制模型,进而使IL-2治疗过程的控制更易于临床实现.本文主要分析IL-2最优注射速度的特征和确定治疗末端时间tf使所得最优系统解的唯一性成立.在文献[2, 4, 6-8]中,考虑最优系统解的唯一性均需要治疗末端时间tf充分小.本文将给出保证最优系统解的唯一性时治疗末端时间tf的估计式.利用数值模拟,说明在最优控制下加入IL-2的免疫治疗能够有效增加HIV感染者血浆中的CD4+T细胞浓度且减少游离病毒浓度.
HTML
-
对于模型(3),假设初始条件为
显然,模型(3)在初始条件(4)下的解均是非负的.于是对其解,由模型(3)的第2个方程有V′≤
$\left( {\frac{g}{{{b_2}}} - {\mu _2}} \right)V\left( t \right)$ .这意味着当${\frac{g}{{{b_2}}}}$ ≤μ2时有$\mathop {\lim }\limits_{t \to \infty } V\left( t \right)$ =0,所以当${\frac{g}{{{b_2}}}}$ ≤μ2时游离病毒将会自然清除,不需要介入治疗.因此,本文将仅讨论${\frac{g}{{{b_2}}}}$ > μ2的情形.因为任何药物治疗均存在副作用,所以一般治疗周期时间均有限,同时CD4+T细胞的浓度代表感染者的免疫能力,于是本文以皮下注射IL-2的速度VI为控制变量,记治疗末端时间为tf,定义目标函数
其中β表示权重,体现治疗的收益和代价.容许控制集为
VI为可测函数,VIM为IL-2注射最大速度.这里最优控制的效果是在[0,tf]内使得CD4+T细胞浓度较大,同时注射IL-2速度较小,从而减少药物带来的副作用.因此,本文的目标是寻找最优控制VI*,使得
类似的目标函数和最优控制问题可参见文献[4, 8-13].关于该问题最优控制变量的存在性可用文献[4, 8-12, 14]的方法(或定理)证明.
-
由于满足模型(3)及初始条件(4)的解使得目标函数(5)取最大值时,最优控制VI*存在,因此可用Pontryagin最大值原理[15]推得该问题最优控制的必要条件.为了易于理解最优控制的确定过程,本文借鉴文献[4, 9, 12]中引入惩罚乘子的方法.
定理1 假设最优控制为VI*,模型(3)满足初始条件(4)的相应解为T*,V*,I*,则存在协状态变量λ1,λ2,λ3满足
横截条件为
最优控制VI*的表达式为
证 构造Hamilton函数
其中w1(t),w2(t)≥0均为惩罚乘子.在容许控制集U的范围内,当VI=VI*时,惩罚乘子w1(t)和w2(t)满足
由Pontryagin最大值原理,λ1,λ2,λ3满足的协状态方程为
由于VI*为系统(3)在目标函数(5)下的最优控制变量,当VI=VI*时,
$\frac{{\partial H}}{{\partial {V_I}}} = 0$ ,即由惩罚乘子w1(t)和w2(t)满足的条件(6)可知,当0 < VI*(t) < VIM时,w1(t)=w2(t)=0;当VI*(t)=0时,w2(t)=0;当VI*(t)=VIM时,w1(t)=0.于是由(7)式有,当0 < VI*(t) < VIM时,VI*(t)=
$\frac{{{\lambda _3}}}{\beta }$ ;当$\frac{{{\lambda _3}}}{\beta }$ ≤0时,VI*(t)=0;当$\frac{{{\lambda _3}}}{\beta }$ ≥VIM时,VI*(t)=VIM.因此,最优控制VI*的表达式为由文献[15]中横截条件,得λ1(tf)=0,λ2(tf)=0,λ3(tf)=0.证毕.
根据定理1,所求的最优系统为
-
为了简化最优系统解的唯一性的证明过程,下面给出一个关于函数u(γ)的引理,其中u(γ)=maxρ,minη,γ,这里ρ,η为常数.
引理1 对于函数u(γ),当ρ < η时,有u(γ1)-u(γ2)≤γ1-γ2,其中γ1,γ2∈
$\mathbb{R}$ .证 引理1容易证得,故证明略去.
定理2 当tf充分小时,最优系统(8)的解是唯一的.
证 假设最优系统(8)存在两个解分别为T,V,I,λ1,λ2,λ3和T,V,I,λ1,λ2,λ3.令
和
其中m > 0.
将式(9)分别代入系统(8)的6个方程,得
再将式(10)分别代入系统(8)的6个方程,得
由系统(11)的第1个方程和系统(12)的第1个方程,得
由于系统(8)的状态变量T,V,I和协状态变量λ1,λ2,λ3在[0,tf]上均有界,因此存在正数xs,ys,zs,ps,qs和rs,使得0≤x≤xs且0≤x≤xs,0≤y≤ys且0≤ y≤ys,0≤z≤zs且0≤z≤zs,p≤ps且|p|≤ps,q≤qs且|q|≤qs,|r|≤rs且|r|≤rs.于是由式(13)可得
进一步,根据x和z的有界性,由(14)式可得
为后续表述简单,记
则由不等式(15)可得
由初始条件T(0)=T0有x(0)=x(0),即X(0)=0.将不等式(17)两端关于t在[0,tf]上积分,得
其中
同理,根据系统(11)的第2个方程和系统(12)的第2个方程得
其中
令
由引理1可得
同理,根据系统(11)的第3个方程和系统(12)的第3个方程,得
其中
又根据系统(11)的第4个方程和系统(12)的第4个方程得
类似于不等式(14)和(15)的推导,并应用式(16)中引入的记号,由式(21)可得
由横截条件λ1(tf)=0有p(tf)=p(tf),即P(tf)=0.将不等式(22)两端关于t在[0,tf]上积分,得
其中
同理,由系统(11)的后两个方程和系统(12)的后两个方程可得
其中
于是,由不等式(18),(19),(20),(23)和(24)可得,
由于不等式(25)的第一项是非负的,所以有
进一步利用不等式M2+N2≥2MN,由式(26)可得
其中
这里
再由于区间[0,tf]上e-2mt≤1恒成立,将函数G1进一步缩小,有
其中
因此,由式(27)有
$\int_0^t {{G_2}{{rm d}}t \le 0} $ .由于Ai(i=1,2,…,5)和Bj(j=1,2,3)均为不依赖于m和t的正常数,所以有
若m1=C1+A1,m2=C2+A2+B1,m3=C1+A4+B2,m4=C2+A5+B3,m5=
$ \frac{1}{{2\beta }}$ +C3+A3,则当m > maxm1,m2,m3,m4,m5时,Θl(m,0) > 0(l=1,2,…,5).所以,对应足够大的正数m,存在充分小的正数tf,使得Θl(m,tf) > 0(l=1,2,…,5).于是,由式(28),对应t∈[0,tf]有因此T(t)=T(t),V(t)=V(t),I(t)=I(t),λ1(t)=λ1(t),λ2(t)=λ2(t),λ3(t)=λ3(t).证毕.
结合临床实际情况,通常期望保证最优系统解唯一的治疗末端时间tf能够尽可能较大.当m > maxm1,m2,m3,m4,m5且tf满足下列条件时,不等式(28)中Θl(m,tf) > 0(l=1,2,…,5)成立:
1) 1≤emtf <
$\frac{{m - {C_1}}}{{{A_1}}}$ ,即$0 \le {t_f} < \frac{1}{m}\ln \frac{{m - {C_1}}}{{{A_1}}}$ .2) 1≤emtf <
$\frac{{ - {A_2} + \sqrt {A_2^2 + 4{B_1}\left( {m - {C_2}} \right)} }}{{2{B_1}}}$ ,即$0{t_f} < \frac{1}{m}\ln \frac{{ - {A_2} + \sqrt {A_2^2 + 4{B_1}\left( {m - {C_2}} \right)} }}{{2{B_1}}}$ .3) 1≤emtf <
$\frac{{ - {A_4} + \sqrt {A_4^2 + 4{B_2}\left( {m - {C_2}} \right)} }}{{2{B_2}}}$ ,即$0 \le {t_f}<\frac{1}{m}\ln \frac{{ - {A_4} + \sqrt {A_4^2 + 4{B_2}\left( {m - {C_1}} \right)} }}{{2{B_2}}}$ .4) 1≤emtf <
$\frac{{ - {A_5} + \sqrt {A_5^2 + 4{B_3}\left( {m - {C_2}} \right)} }}{{2{B_3}}}$ ,即$0{t_f} < \frac{1}{m}\ln \frac{{ - {A_5} + \sqrt {A_5^2 + 4{B_3}\left( {m - {C_2}} \right)} }}{{2{B_3}}}$ .5) 1≤emtf <
$\frac{1}{A_{3}}\left(m-C_{3}-\frac{1}{2 \beta}\right)$ ,即$0 \leqslant t_{f}<\frac{1}{m} \ln \left[\frac{1}{A_{3}}\left(m-C_{3}-\frac{1}{2 \beta}\right)\right]$ .因此,当m > maxm1,m2,m3,m4,m5时,若0≤tf < Tf=mint1,t2,t3,t4,t5,则最优系统(8)在区间[0,tf]上的解唯一,其中
-
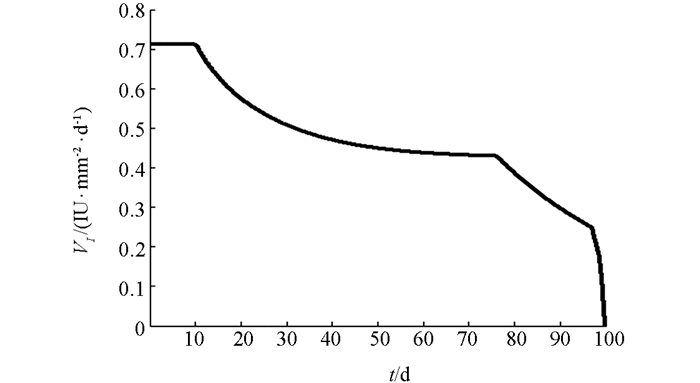
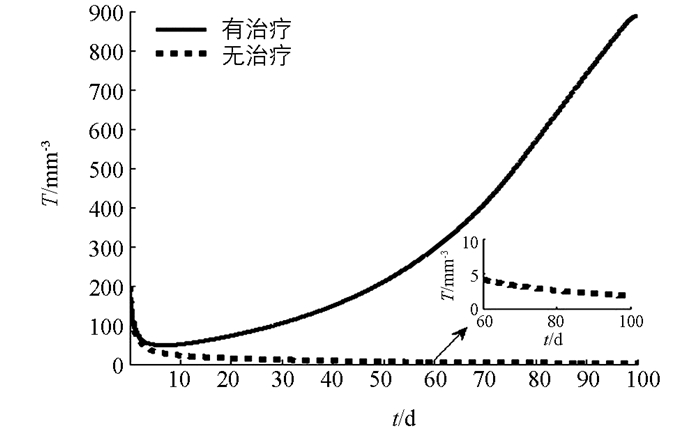
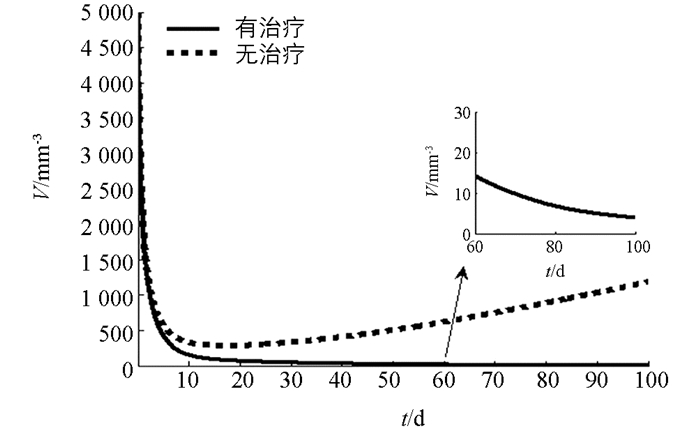
下面利用数值模拟分析在最优控制下免疫治疗药物IL-2对HIV感染者的治疗效果.本文取治疗周期为100 d(即tf=100 d),初始值为T0=200 mm-3,V0=5000 mm-3,I0=0IU·mm-2.由文献[3, 5],取s1=2.0mm-3·d-1,s2=1.5 mm-3·d-1,b1=14 mm-3,b2=1 mm-3,μ1=0.002 d-1,μI=10 d-1,k=2.5×10-4 mm3·d-1,g=30 mm-3·d-1.对其余参数进行估计,令β=50,μ2=0.000 2 d-1,c=0.006 8 mm3·d-1,a=0.8 mm2·IU-1·d-1,VIM=1IU·mm-2·d-1.数值模拟结果见图 1-3.由图 1知,最优注射速度VI*在前10 d左右持续为0.711 2 IU·mm-2·d-1,之后开始减少.由图 2和图 3知,在最优控制下,加入IL-2的治疗能够增加CD4+T细胞浓度且减少游离病毒浓度,但并不能彻底清除病毒.






 DownLoad:
DownLoad: