-
高压共轨电控燃油喷射系统已逐渐应用于柴油发动机,燃油经过泵体从喷油管进入公共供油管,通过公共供油管内的油压实现喷射压力和喷射时间的精确控制,确保了发动机高效率、低油耗[1-2]地工作.由于燃油进入和喷出的间歇性工作过程会导致高压油管内的燃油压力发生波动,使得所喷出的燃油量出现误差,影响发动机的工作效率,甚至对燃油喷射系统的稳定性产生影响,引起系统的失效和故障[3-4].维持高压油管的压力稳定是燃油喷射系统性能的保障,通过试验仿真可以指导燃油喷射系统的设计,有效减少试验工作量及试验费用.
传统喷射系统的仿真过程会采用GT-FUEL,HYDSIM,ANSYS等商用仿真软件得到系统喷油规律以及各个部分的压力变化,主要用作优化喷油系统中阀体内部结构,分析系统关键结构参数对喷油性能的影响[5-8].其中,文献[9]采用ANSYS软件使用电磁—机—液三维联合仿真方法,得到阀芯动态响应特性和流场特征参数随阀口开度的变化规律.文献[10]通过AMEsim软件建立一维液力仿真模型,分析了高压油管结构参数对燃油系统性能的影响.文献[11]给出了凸轮的最优曲线设计使油泵提供持续稳定的燃油压力,可以提高喷射系统的系统稳定性.文献[12]通过实验和数值研究了燃油压力特性及其与电磁阀瞬态运动的关系,提出了一种基于4个燃油压力特征点的燃油喷射量预测方法,可以较好预测每个周期的燃油喷射量.
凸轮的角速度控制是维持高压油管压力稳定,减少燃油喷出量误差的关键因素之一,但要计算凸轮的最优角速度来使得高压油管内的喷油量稳定,直接采用仿真软件来求解比较困难,需要进行复杂的仿真参数设置与大量的数值计算来逼近最优值[7, 9, 12].本文针对高压共轨燃油系统中的高压油管的压力稳定问题,简化喷油系统复杂的工作过程,通过分析高压油泵燃油压力变化过程、喷油器喷嘴的流量喷射过程以及高压油管内的压力与密度变化过程,建立凸轮转动角速度的优化数学模型,通过Matlab求解最佳凸轮转动角速度,使得高压油管内的压力尽量稳定,减少所喷出燃油量的误差.
HTML
-
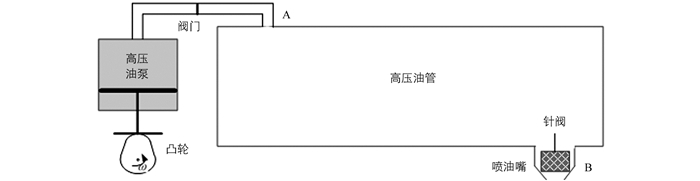
设高压油管的推荐工作压力在100 MPa,体积为V1,mm3,如图 1所示,高压油管的燃油来自高压油泵,凸轮驱动柱塞上下运动.在柱塞腔出口有一个单向阀门,当柱塞腔的压力大于高压油管内的压力时,柱塞腔与高压油管链接的单向阀开关开启,燃油进入高压油管内. 图 1中A处孔径直径为dA,mm. 图 1中喷嘴器内部有一个针阀,针阀作周期运动,当针阀升程为0时,针阀关闭;针阀升程大于0时,针阀开启,燃油通过喷孔喷出.本文主要研究喷射系统的喷射过程与油泵的输油过程,将对分析过程作以下简化:①忽略燃油温度的变化;②假设柱塞腔与高压油管内的燃油状态均匀.
其中ρ是燃油的密度,E是弹性模量,E随压力P越大而增大.进入高压油管的单位时间流过小孔的燃油体积为[16]
其中C是流量系数,SA是小孔面积,mm2,ΔP为小孔两边的压力差,MPa.
通过确定凸轮的角速度ω,rad/ms,使得高压油管内的压力稳定在100 MPa左右.以下将分别分析柱塞腔、高压油管的压力与密度变化以及喷嘴流量的变化过程,最后建立最佳凸轮转动角速度的优化模型.
-
柱塞向上运动时将压缩柱塞腔内的燃油,当柱塞腔内的燃油压力大于高压油罐内的压力时,柱塞腔与高压油管连接的单向阀开启,燃油从A处进入高压油管.柱塞腔内直径d2=5 mm,对应横截面积为S2,柱塞运动到上止点位置时,柱塞腔残余容积为V0,柱塞运动到下止点时,低压燃油会充满柱塞腔,低压燃油的压力与密度分别为P0=0.5 MPa,ρ0=0.804 5 mg/mm3.
令PU(t)为柱塞腔在t时刻的压力,MPa,ρU(t)为高压燃油在t时刻的密度,mg/mm3,凸轮在旋转到不同角度时对应的极径为r(α),mm,其中α=ωt.假设当t=0时,α=0,柱塞运行在下止点位置.以下把柱塞上升与下降两个过程分开讨论.
1) 当2kπ≤α<2kπ+π时,柱塞向上运动压缩燃油,PU(t)不断上升,根据公式(1),柱塞腔内燃油压力与密度的单位时间变化过程为
其中初始状态PU(0)=P0.当PA(t)大于高压油管压力P(t)时,单向阀门打开,根据公式(2),经过A处流入高压油管的单位时间燃油质量为
其中流量系数C=0.85.根据柱塞腔内燃油质量MU(t)与密度、体积的计算关系,有
其中V2(t)是t时刻柱塞腔内的燃油体积,V2(t)=S2×h(t)+V0,h(t)是t时刻柱塞距离上止点位置的距离,mm. h(t)由凸轮的上下运动方程给出,
其中Hmax是柱塞运行到上止点距离极径中心(凸轮圆心)的距离.
显然单位时间内MU(t)变化量就是流入高压油管质量Min(t)的相反数,即
根据公式(4)与公式(5),柱塞腔内燃油密度变化方程为
其中初始状态
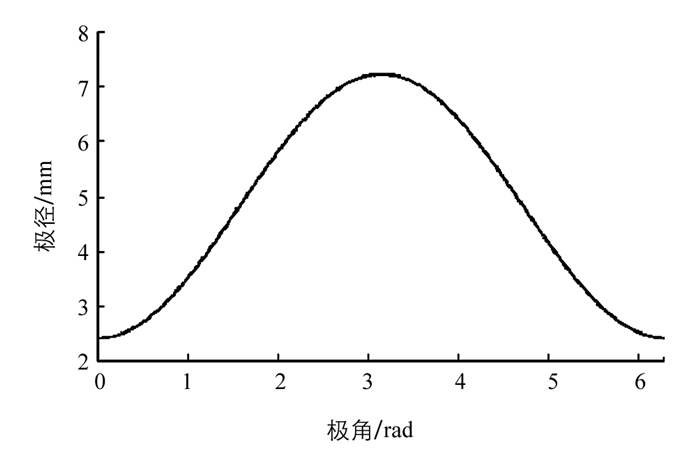
${\rho _U}(0) = {\rho _0}, \frac{{{\rm{d}}h}}{{{\rm{d}}t}} $ 需要r(α)的离散测量点来近似计算,根据公式(6),图 2给出了0≤α<2π一个周期内r(α)的变化过程,每个测量点是等距的,即Δα=αi+1-αi相同,我们通过线性插值来求出r′(α),其中每一个离散测量点αi的导数的一阶差分计算为
对于αi≤α<αi+1,令ξ=(α-αi)/(αi+1-αi),有
2) 当2kπ+π≤α<2kπ+2π时,柱塞在到达上止点后开始往下运动,此时柱塞腔与低压油腔相通,开始注入低压燃油,PU(t)迅速下降至P0,这段时间单向阀门一直关闭.凸轮运行至下止点时,PU(t)=P0,ρU(t)=ρ0,为了简化这段变化过程,设置以下微分过程满足以上分析过程:
-
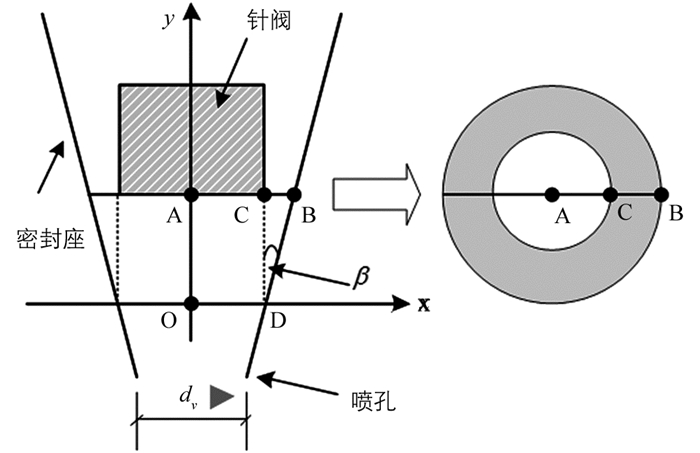
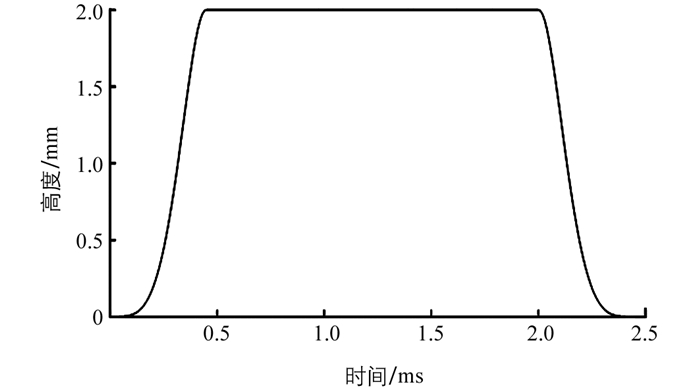
喷油器设定了每T0=100 ms工作一次,喷油器喷嘴结构如图 3所示,针阀直径为dV=2.5 mm,密封座是半角为β=9°的圆锥,喷孔直径为dB=1.4 mm,面积为SB.针阀升程大于0时,针阀开启,燃油开始向喷孔流动并喷出.在一个喷油周期内针阀升程的高度与时间的关系H(t)如图 4所示,针阀从t=0开启,当t=0.45 ms时升程达到最大,然后一直保持到t=2 ms后开始下降,一直到t=2.45 ms后升程恢复为0,针阀关闭,然后到下一个喷油周期100 ms后,针阀升程重新开始上升.
我们将对燃油射流速度影响较少的因素排除,找出影响喷孔燃油射流速度的主要因素,简化计算公式.根据单位质量不可压缩流体在稳定流动条件下的伯努利方程[16],可得喷孔处的流体喷出速度为
可以看到燃油喷出速度与燃油的压力和密度有关.另一方面,针阀升程会影响喷口实际喷油质量,当升程较小时,喷口面积等于针阀与密封座之间空隙的面积;当升程较大时,空隙面积增大,喷口面积等于喷孔面积.令针阀升程H=H0时,针阀与锥形内壁形成的燃油排出面积SZ与喷孔面积SB相等.那么,当针阀升程H≤H0时,燃油喷出的喷口面积以SZ(t)计算,当针阀升程H>H0时,燃油喷出的喷口面积以SB计算.则在一个喷油周期内,单位时间内的流出的燃油质量为
其中C1=0.8是流量系数.如图 3,针阀升程高度H=|AO|,当H大于0时,针阀处形成的喷口形状是一个圆环状,圆环面积为.
令SZ=SB,可以得到H0的表达式,
-
高压油管内的压力与密度变化源自于喷油嘴B处向外的喷油量,以及高压油管A处的燃油进入量.根据公式(4)与公式(13),可分别得到高压油管内压力P(t)与密度ρ(t)单位时间的变化过程:
其中V1是高压油管体积.初始状态P(0)=100 MPa,ρ(0)=0.850 0 mg/mm3.
-
综合公式(3),(7),(11),(14),得到了柱塞腔与高压油管状态完整的动态变化过程,待确定的参数是凸轮的角速度ω.为了考查高压油管的压力稳定性,定义在一个充分长的时间T,T≫T0,通过寻找最优的ω,使得高压油管的压力尽量稳定在100 MPa.令目标函数F(ω)为高压油管在时间T内与100 MPa的误差平方和,
另一种合理的目标函数可以设置为,在时间T内高压油管压力P(t)的最大变化幅值,
因为初始压力为100 MPa,且压力是周期变化的,采用最大变化幅值可以反映压力的稳定性.最后,求解使目标函数F(ω)数值最小的ωopt,
1.1. 问题描述
1.2. 油泵内燃油的压力变化过程
1.3. 喷油器喷嘴的流量喷射过程
1.4. 高压油管内燃油的压力与密度变化过程
1.5. 最优凸轮角速度的优化模型
-
本文通过Matlab 2018A对上述建立的非线性常微分方程组进行数值求解,其中用到了Matlab的ode45函数,它实现了四阶—五阶Runge-Kutta算法,是一种自适应步长的微分方程数值解法,具有较高的计算精度,其整体截断误差为(Δt)5[17-18]. ode45函数默认设置了Δt=0.1(tmax-tmin),其中tmax与tmin分别是常微分方程组的左右区间上的端点值.由于计算的T很大,针阀开启的时间很短,只发生在2.45 ms以内,并且凸轮的上升运动,也会导致PU较大变化,需要较小的计算步长Δt来确保较小的整体截断误差.通过设置odeset的MaxStep参数来控制计算步长:
deltaT= 0.01;
opts = odeset(‘MaxStep’,deltaT);
tspan = [0,T];
[t,y] = ode45(@myfun,tspan,y0,opts);
其中opts定义了步长为0.01 ms,myfun定义了公式(3),(7),(11),(14)的微分方程组,tspan是微分方程组的数值计算区间,T在这里设置为10 000 ms,共100个喷油周期,y0是微分方程的初始值.由于步长比较小,整个计算过程所需耗时较长,需要较长时间计算F(ω),如果要高计算速度,可以采用求解微分方程的其他求解函数如ode23等,但计算精度会相应降低.
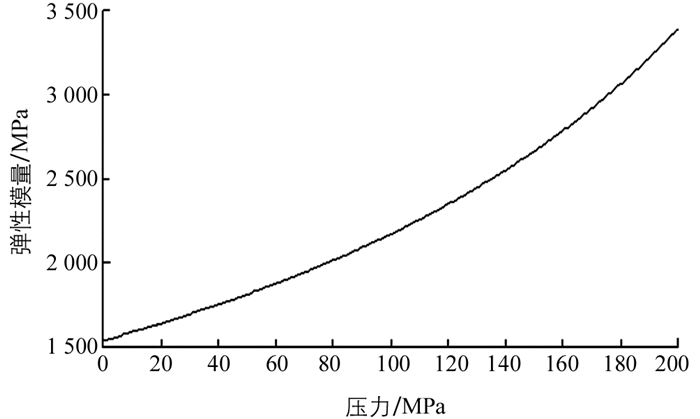
在计算公式(3)与公式(14)前,需要先确定燃油弹性模量E与压力P的对应关系E(P). 图 5给出燃油压力在[0, 200]MPa范围内对应的弹性模量的散点数据图,曲线上的每一个点对应实测数据(Ei,Pi).通过线性插值求得每个压力P所对应弹性模量的数值E(P).具体地,对于Pi≤P<Pi+1,令γ=(P-Pi)/(Pi+1-Pi),
最后采用Matlab的fminsearch来求解,需要设置一个合理的初始值ω0,使数值计算更快地收敛,减少计算时间.可以简化设置高压油管的压力P与密度ρ分别恒定在100 MPa与0.850 0 mg/mm3,然后根据公式(13)与公式(4),可以近似估算在一个喷油周期的燃油喷出量Qout≈31.00 mg,一个凸轮周期内燃油进入高压燃油的进入量Qin≈75.27 mg,从而得到ω0=0.025 89 rad/ms.本文目标函数采用公式(16),最后求得最优的角速度ωopt=0.025 85 rad/ms,对应凸轮工作周期Topt为243.06 ms.
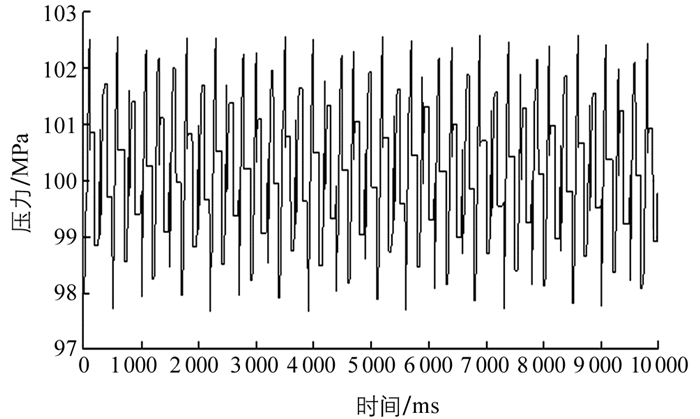
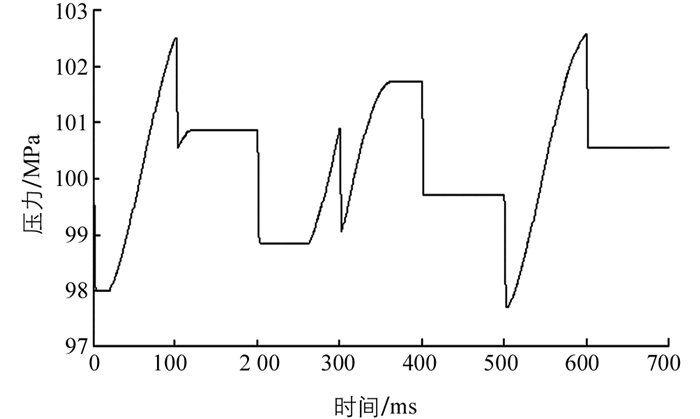
图 6给出了在10 000 ms时间内高压油管的燃油压力变化,可以看到整个压力比较稳定地在97.6~102.6 MPa的压力区间内变化,变化的最大幅度为4.87 MPa,压力最大值为102.57 MPa,主要发生在凸轮到达上止点位置,最小值为97.70 MPa,主要发生在2.45 ms内的喷油过程.为了更清楚看出高压油管内的燃油压力变化,图 7给出了高压油管在700 ms内的压力变化,可以看到在每个喷油周期(100 ms的整数倍)前2.45 ms内压力明显急速下降,随着凸轮上升,推动燃油进入高压油管,其压力也随之上升,并在100 MPa附近波动.
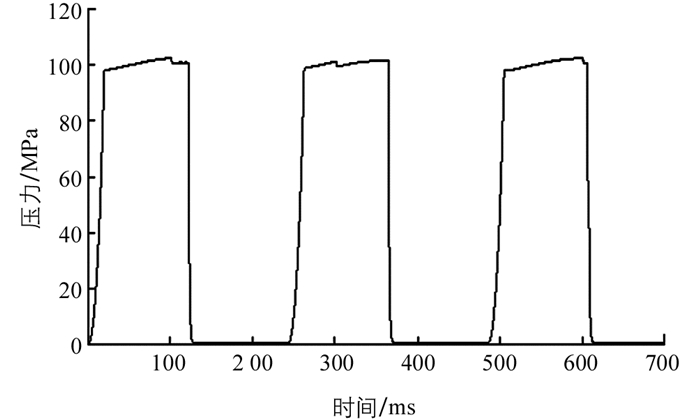
柱塞腔内的燃油压力随着凸轮周期上下运动而变化,图 8给出700 ms内燃油压力变化的过程,随着凸轮上升,燃油压力迅速上升,在53.2 ms时超过100 MPa,此时单向阀门打开,燃油通过A处持续进入高压油管内,压力略高于高压管的压力值.当凸轮到达上止点并往下运动时,即
$t > \frac{{{T_{{\rm{opt }}}}}}{2} $ ,柱塞腔压力迅速下降到100 MPa以下,单向阀门关闭,柱塞腔开始注入低压燃油,此时燃油压力一直在0.5 MPa.以上仿真过程是针对喷油周期T0=100 ms下求出的凸轮最优角加速度. 表 1给出了在不同喷油周期T0下求解的凸轮最优角速度ωopt,以及对应凸轮工作周期Topt.可以看出随着喷油周期变化,凸轮最优工作周期Topt与T0具有较强的线性关系.
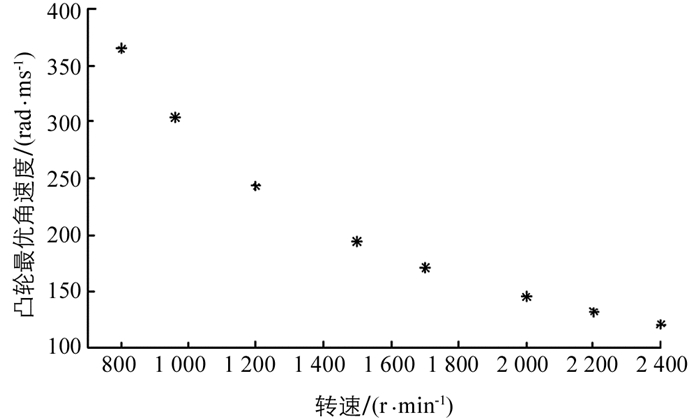
表 1最后一列给出了不同喷油周期所对应发动机的转速大小,对于四冲程柴油发动机,曲轴旋转两周,对应一次喷油周期,即转速n=2×60×1 000/T0=120 000/T0,r/min.由于柴油发动机的转速一般不高,普遍在3 000 r/min以下,经济转速一般在1 500 r/min左右,表 1讨论的喷油周期及转速的数值范围基本反映了一般柴油机的工作状态.为了更好反映凸轮最优角加速度与发动机转速的对应关系,图 9给出了柴油发动机常用转速与对应凸轮最优角加速度的关系图,随着转速增大,凸轮最优角加速度也逐渐变小.
柴油机在实际连续运作中,发动机的转速是连续变化的,可根据本文方法进一步扩充表 1的实验数据,通过数值插值或数据拟合等方法,获取凸轮最优转速的变化调整,这将是以后进一步的研究工作.
-
本文针对高压共轨电控燃油喷射系统中的高压油管的压力稳定问题,通过对高压油管内复杂燃油压力与密度的变化关系进行分析,分别获取柱塞腔、高压油管的压力与密度变化,以及喷嘴的流量变化过程,最终建立了凸轮角加速度的优化模型,采用Matlab的ode45与fminsearch函数进行数值计算,获得最优的凸轮角速度,使得高压油管在工作过程中压力基本稳定在指定工作压力中,压力变化的最大幅度为4.87 MPa.本文的研究方法可为燃油喷射系统的喷油精准控制设计提供参考,减少试验工作量及试验费用.






 DownLoad:
DownLoad: